
刺し子模様をPythonで描く:斜眼を使う・紗綾形
刺し子模様を手で描くとき,ものによっては斜眼用紙を使う。たとえば,麻の葉。基本パターンを作るのにこんな図を使った。

この背景が斜眼。正三角形になっている。この図はCinderellaで作った。
見出し画像は,斜紗綾形。これも背景を見てわかる通り斜眼だ。
Cinderellaでは,標準的な作図機能として,方眼とどちらかを選べるようになっている。「正三角形」と書いたが,実際には平行四辺形だ。上の図でいうと,点Cの位置(座標)は,右へ2,斜め上に2で ( 2 , 2 ) と考える。
斜眼の考え方
斜眼は,斜交座標系である。横軸と縦軸が斜めに交わっているもので,座標を次のようにとる。

これを,通常の直交座標系で表せばよいのだが,そのためには,ベクトルの知識を使う。高校で習ってはいるはずだが,忘れている人は多いだろう。現役高校生にはちょうどいい教材になる。まあ,さっと読み飛ばしても構わない。
まず,通常の直交座標系で,ある点の位置をベクトルで表す方法を考えよう。これは教科書に載っている。
横軸方向の基本ベクトル(長さ1のベクトル)を ex,縦軸方向の基本ベクトルを ey とすると,点(3,2) は 3ex+2ey と表せる。(ex.eyはベクトル)

縦軸を斜めにしても同様に表せる。

そこで,基本ベクトル ex とey の成分を直交座標で表せば,斜交座標の点を直交座標に直せる。それが,次のプログラム。
def syagan(plist):
ex = np.array([1, 0])
ey = np.array([0.5, np.sqrt(3)/2])
ret = []
for i in range(len(plist)):
p = plist[i]
ret.append(list(p[0]*ex + p[1]*ey))
return ret斜眼には,もう一つ,横軸を斜めにしたものもある。

この2つを使い分けられるように,引数に stype :1か2 を入れて,次のように定義してこれから使っていこう。
def syagan(stype,plist):
if stype == 1:
ex = np.array([1, 0])
ey = np.array([0.5, np.sqrt(3)/2])
else:
ex = np.array([np.sqrt(3)/2, 0.5])
ey = np.array([0, 1])
ret = []
for i in range(len(plist)):
p = plist[i]
ret.append(list(p[0]*ex + p[1]*ey))
return ret麻の葉
これを使って,麻の葉を描いたのが次のプログラムだ。座標の取り方を,直交座標系のときと比べてみよう。
なお,syagan の定義を追加し,basicpattern() の定義をこれに変えただけで他は同じである。(他は省略。図も同じなので省略)
# 斜眼への変換
def syagan(stype,plist):
if stype == 1:
ex = np.array([1, 0])
ey = np.array([0.5, np.sqrt(3)/2])
else:
ex = np.array([np.sqrt(3)/2, 0.5])
ey = np.array([0, 1])
ret = []
for i in range(len(plist)):
p = plist[i]
ret.append(list(p[0]*ex + p[1]*ey))
return ret
# 基本パターンをorgを原点として描く
def basicpattern(org):
A = [0, 0]
B = [2, 0]
C = [2, 2]
D = [4, 0]
E = [6, 0]
F = [4, 2]
G = [4, 4]
H = [2, 4]
K = [0, 4]
L = [-2, 4]
M = [0, 2]
N = [0, 6]
draw(org, syagan(1, [A, B, C, D, E, F, G, H, C, K, L, M, A, G]))
draw(org, syagan(1, [E, L]))
draw(org, syagan(1, [F, M]))
draw(org, syagan(1, [C, N]))紗綾形
紗綾形(さやがた)。

複雑に見えるが,基本パターンは一筆書きで描ける。

対称形なので,原点対称として座標を拾う。点は28個ある。
プログラムは,麻の葉と同じで,basicpattern(org) の定義と,描画設定を変えればよい。
def basicpattern(org):
p1 = [-8, 1];
p2 = [-1, 8];
p3 = [-0, 7];
p4 = [-1, 6];
p5 = [-0, 5];
p6 = [-1, 4];
p7 = [-2, 5];
p8 = [-3, 4];
p9 = [4, -3];
p10 = [5, -2];
p11 = [4, -1];
p12 = [5, 0];
p13 = [6, -1];
p14 = [7, 0];
p15 = [8, -1];
p16 = [1, -8];
p17 = [0, -7];
p18 = [1, -6];
p19 = [0, -5];
p20 = [1, -4];
p21 = [2, -5];
p22 = [3, -4];
p23 = [-4, 3];
p24 = [-5, 2];
p25 = [-4, 1];
p26 = [-5, 0];
p27 = [-6, 1];
p28 = [-7, 0];
draw(org,[p1, p2, p3, p4, p5, p6, p7, p8, p9,p10,
p11, p12, p13, p14, p15, p16, p17, p18, p19,p20,
p21, p22, p23, p24, p25, p26, p27, p28,p1]
)描画面設定は,たとえば
plt.figure(figsize=(10, 10))
plt.axis([-0, 50, 0, 50])
とし,描画設定を
Shiftx = np.array([10, 0])
Shifty = np.array([0, 10])
Drawcolor = 'k'
drawpattern(10, 10)
とする。
斜紗綾形
紗綾形にも斜眼を用いた斜紗綾形というのがある。
次の図はCinderellaの斜眼を用いて作ったが,紙に描いてももちろんいい。
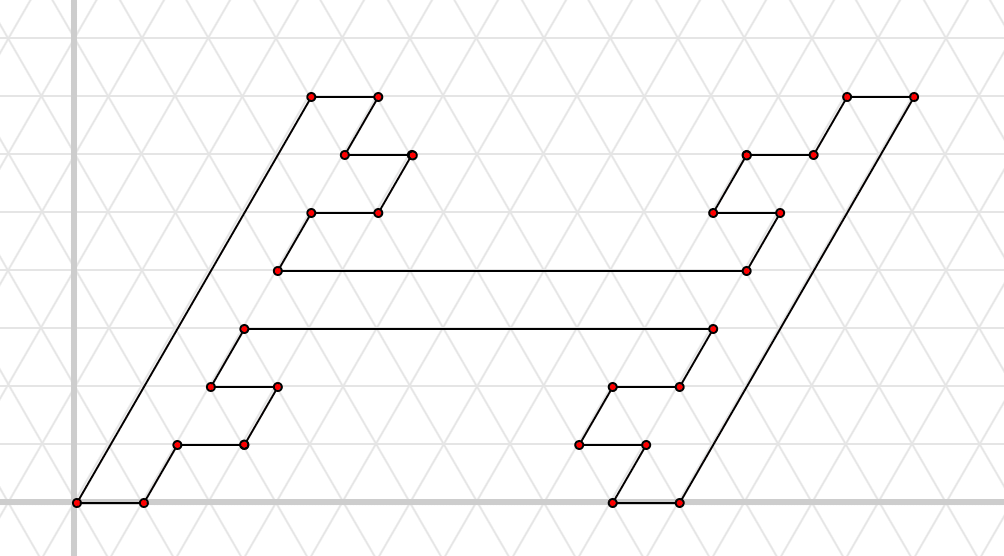
これが基本パターンで,つなぐと次のようになる。

座標のとり方を変えて syagan()で変換する。
# 基本パターンをorgを原点として描く
def basicpattern(org):
p1 = [0, 0]
p2 = [1, 0]
p3 = [1, 1]
p4 = [2, 1]
p5 = [2, 2]
p6 = [1, 2]
p7 = [1, 3]
p8 = [8, 3]
p9 = [8, 2]
p10 = [7, 2]
p11 = [7, 1]
p12 = [8, 1]
p13 = [8, 0]
p14 = [9, 0]
p15 = [9, 7]
p16 = [8, 7]
p17 = [8, 6]
p18 = [7, 6]
p19 = [7, 5]
p20 = [8, 5]
p21 = [8, 4]
p22 = [1, 4]
p23 = [1, 5]
p24 = [2, 5]
p25 = [2, 6]
p26 = [1, 6]
p27 = [1, 7]
p28 = [0, 7]
plist = [p1, p2, p3, p4, p5, p6, p7, p8, p9, p10,
p11, p12, p13, p14, p15, p16, p17, p18, p19, p20,
p21, p22, p23, p24, p25, p26, p27, p28, p1]
draw(org, syagan(1, plist))画面設定の平行移動量を変える。
Shiftx = np.array([10, 0])
Shifty = np.array([15/2, 5*np.sqrt(3)/2])
斜眼のものは,斜交座標で取ったほうが簡単になる。ただし,ちょっと慣れる必要があるかもしれない。
