文系の僕がゼロから学ぶ数学：１から100を足し算したら？等差、等比数列をマスターせよ！

「ねぇねぇ、お父さん。１から100を全部足したら、いくつになるの？？」

と、あなたのかわいい愛娘さんに聞かれた時に、

読者のみなさんは、瞬時に答えることができるだろうか。
まさか、、、、

「うーん、ちょっとわからないなぁ。。」

なんて答えてないだろうか。
娘さんの前でそんなカッコ悪いパパの姿、見せてしまって良いのか。

否である。
カッコ良いパパになりたいなら、

「カナコ、公式さえマスターしておけば簡単さ。5050だよ。」

こう答えたい。いや、答えなければならない。
僕も、将来のこどものために（＊全く未定）、カッコ良いパパになりたい。

そこで、今日は。愛すべき、愛娘、愛息子のために、

１から100を足し算を瞬時に答えられる大人になる。

そんな目標に向かって読者の皆さんと、等比数列、等差数列を学んでいきます！
文系の僕でも理解できる内容で、お伝えしますのでご安心ください！！笑
（＊理系の皆さん、ごめんなさい。。）

■等比数列を逃避した、僕。

等比数列を逃避し、等差数列を遠ざけた、僕。

「じゃあ、今日は等比数列、等数列の勉強始めます。まずは、公式から覚えるように。」

でた、、、数学の公式。
数学の公式は、僕にとってはすべてが暗号だ。

ただただひたすら覚える、英単語と同じようなものだった。

「忘れないようにノートにメモしておいてください。」

やたら丁寧な男性数学教員の言葉遣いに、嫌気が差す。
なぜかこのイケメン数学の教師は、頭も冴えてると来ている。

文系の僕らの気持ちなど知る由もない。
ノートにメモしても覚えられない、理解できないからこっちは困っているのだ。

「はい、こちらが等差数列、等比数列の公式です。」

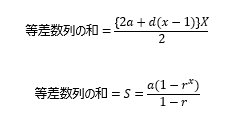
ぷしゅーーー、頭から煙が噴き出す。

暗号や、暗号。

とにかく、メモに取る。
そして、メモを見返す。

あーもう、既に楔方文字にしか見えない。

「これ、テストにでますから、覚えておいてくださいね。」

「じゃな、練習問題やってみましょうか。」

なめんな！！！

当然、僕の中間試験の結果が散々だったことは言うまでもない。

そんな悔しい思いをしてきた、文系の皆さん。

今日、僕が責任をもって、この公式の意味をお伝えし、

カッコいいパパ、ママになるお手伝いをさせていただきます。

😏

■ひっくり返せば、すべてが解決する。

では、等差数列、等比数列を順番に説明していきます。

まずは、①等差数列です。
等差数列とは、はじめの数に一定の数を足し続ける数列です。

例えば、
１、３、５、７、９、、、、、
２、６、１０、１４、１８

とかですね。足し続ける一定の数のことを、公差と言います。
上の例であれば、公差は２と４ですね。

さてでは、早速冒頭の問題にいってみましょう。

「ねぇねぇ、お父さん。１から100を全部足したら、いくつになるの？？」

こちらの問題も公差１の等差数列です。

１、２、３、４、５、、、、、、１００
こちらの数列を１から100まで足しあげたらいくつになりますか、というのが問題です。

もう公式も忘れた、いやそもそも覚えてすらない僕ら文系人には難問です。
とはいえ、愛娘の前でいちいち計算などしていられない。

必殺技を教えます。

ひっくり返して、足してみる。

です。

以下のように、等差数列をひっくり返してもう一つ並べてみます。
すると、、、、そうです！！

元の数列とひっくり返した数列を、左の数字から順に足しあげていくと、全て101になるんです！

僕はこれを知った時に、衝撃を受けました。

なんて、美しいんだ。

天才数学少年ガウスが先生に問われた時に、導いたら説き方らしいです。

ここまでくれば楽ちんですね！！

足すと101になる組み合わせが、１から100まで100セットあります。
ただし、その合計は２つの数列の合計ですから、÷２をすれば良いわけです。

101×100÷2＝5050

これで答えがでました！これなら暗算でも解けますね。
この考え方で、公差が１であれ、２であれ同様に導けます。

では、公式を考えてみましょう。

例えば、以下のような等差数列があったとします。

２、７、１２、１７、２２、２７、３２

初項（初めの数）=2=a
公差(各数字に足される数)＝5=d

の等差数列です。
数学では、初項をa、公差をdとして表現します。

仮に6番目の27を式で求めようとすると、

27=2+5(6-1)

です。つまり、

27=a+d(x-1)

等差数列のX番目の求める際の公式は、
初項aに、公差dを（x-１）回分足せば良いわけです。

ここは、冷静に考えていただければわかると思います。
5番目の数字を求めるにあたり、公差の５を足しあげるのは、4回。8番目なら7回です。

ですから、公差dに対して、（X-1）をかけて、初項に足せばｘ番目の数字を求めることができます。

では、等差数列のX番目の公式がわかったところで、こちらもひっくり返して足してみましょう。

そうなんです。
こちらも先ほどの同様にひっくり返して足しあげた時の合計が全て、

2a+d(x-1)

になるんです！！
ここまでくれば、等差数列の和の公式もきっとわかるはずです。

先ほどの１から100の計算と同じで、
足しあげた時の数=2a+d(x—1)を、X番目まで足しあげると全部でｘセットあるわけです。
それを、先ほどと同様に÷２、するわけなので、

等差数列の公式がわかりましたね！！
これで、カッコいいお父さんです！！

お疲れかもしれませんが、、、

等比数列も同じ原理なので説明してしまいます！！笑

😆

■かけてずらせば、すべて解決する。

②続いて等比数列です。
等比数列とは同じ数をかける数列のことです。

２、４、８、１６、３２、（２をかけ続ける）
４、１２、３６、１０８、（３をかけ続ける）

それぞれ初項２と４、公比２と３ですね。
ここでは、さっそくX番目の等比数列の数を求めてみましょう。

上の数列で、5番目の３２、４番目の１０８を求める時は、

初項２に、２（公差）を４乗する。
初項４に、３（公差）を３乗する。

することで求めることができます。
つまり、初項(a)×公差(r)（x番目-1）乗で答えが出せます。

が、等比数列のX番目を求める公式です。

続いていきなり和の公式に行く前に、わかりやすくするために具体的な数列で考えてみましょう。

等比数列の必殺技は、

かけてずらす

です。以下のような等比数列で考えみましょう。
①の等比数列に対して、②では①の等比数列を２倍にしてずらしています。
求めたいのは、①の等比数列の和＝Xです。

少しわかりずらいので、式を逆にしましょう。

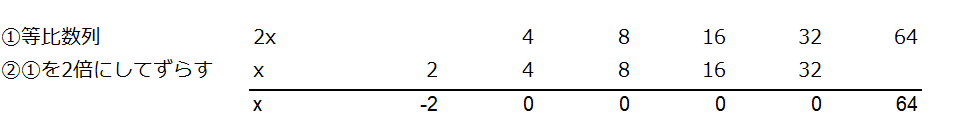
わお、、、

X＝-2 +64= 62

で、一発で答えがでちゃうんですね。２倍してから引き算することで、端の数以外の数が、
全部ごっそり差し引きゼロになっていまうんです。

こちらを先ほどのX番目の公式に置き換えても全く同じです。

先ほどは、公比２の等比数列を２倍しました。
なので、公比がrの場合はｒ倍します。

考えるべきは、初項がﾏｲﾅｽと、r倍したX番目の等比数列を足しあげるだけです。したがい、

ついに、等差数列の和の公式を求めることができました！！

難しく考えずに、ｒに先ほどの2を当てはめて考えればすんなり理解できると思います、試してみてくださいね。

お疲れ様でした！！笑

等差、等比数列の和の公式をマスターしました。

これでばっちり、愛娘、愛息子にどや顔できますね。

😎

■まとめ

さてさて、本日は高校数学の等比数列、等差数列について学んできました。
読者のみなさん、特に文系のみなさん。

いかがでしたでしょうか。

ライクではなく、スッキリボタンをいただきたいところです。

僕も改めて数学を学びながら思うのですが、

数学の公式って、覚えるもんじゃないです。

大切なのは、数学の公式を理解しておくこと、自分でも導けるようになるとです。
僕らが文系人は

数学の公式→暗号→意味不明→やめる。

という負のループに陥っていたのです。
でも、例えば今日の等差数列も、等比数列も。

ひっくり返して足す。

とか、

かけてずらす。

なんてことを学ぶだけで、みなさんも心の中で、

「そういうことだったのかっ！！」

と叫んだ、もしくは膝を打ったのではないでしょうか。
学生時代は、公式のせいで嫌々さけていた数学ですが、
公式の背景や、成り立ちを理解するだけで、全然世界が広がりますよね。

僕は、衝撃を受けました。。。

ガウスさん、天才やん。

と、、、笑

そんな経験は、きっと大人の今からでも遅くないはずです！
みなさんも時間を見つけて、苦手だった数学にトライしてみてはいかがでしょうか。

大人の学びを楽しもう。

誰でも、いつだって学べる。

ではでは、本日はここまでです。
また、明日のnoteでお逢いしましょう。

P.S：理系の読者のみなさんには簡単すぎましたかね笑　文系の私のレベルはこんなもんです、ご勘弁ください！！