
「増殖するG」が引き起こす心理的圧力に関する一考察
こんにちは。沙里葉(Sariha)です。
今回はぴにき@pi_ni_ki様のX上でのポストで言及されていました、「増殖するGが通ることによる心理的負荷」について考察していこうと思います。
全文無料です。
よろしければ最後までお付き合いください。
以下、元ポストです↓
うららやヴェーラーなどの手札誘発で、
— ぴにき (@pi_ni_ki) October 12, 2024
「展開自体が物理的にできなくなった」ことより、
相手の増殖するGを通してしまい、
「展開自体は出来るけど諦めざるを得ない」
ことの方が、ストレス指数は高いんだろうか
心理学に自信ニキYPはnoteで論文投稿お願いします pic.twitter.com/lDx6Hzp4Bn
忙しい人向け
理論とか分析とかどうでもいいから結果だけ知りたい人向けのリンクを貼っておきます.ここをクリック.
背景と目的
遊戯王において、「手札誘発」カードは、相手のターン中に即座に使用できるカードです。
このゲームにおける妨害の主要な要素の一つです。
これらのカードは相手の行動を制限し、展開を妨害することで、自分の勝利を確保するための戦略的ツールとして機能します。
手札誘発カードは、相手ターン中に使用できるため、相手プレイヤーが予期せぬタイミングで介入し、展開を阻害できます。
代表的な手札誘発カードには「灰流うらら(図1)」や「エフェクト・ヴェーラー(図2)」、「無限泡影(図3)」などがあり、これらは相手の特定の行動(ドロー、サーチ、モンスター効果の発動など)を封じる効果を持ち、相手のリソースや展開力を制限するのに役立ちます。



中でも「増殖するG」という手札誘発カードは、他の手札誘発とは異なる特異な影響をもたらします。

増殖するGの効果は、「相手が特殊召喚を行うたびに自分がデッキからカードを1枚ドローできる」というものです。
このため、妨害というよりも「圧力」をかける性質を持っています。
増殖するGが使用された場合、相手はその後の特殊召喚を行うたびにプレイヤーにカードアドバンテージを与えることになります。
これを続けるほど、相手に有利な状況を作り出してしまいます。
このため、増殖するGが通った場合、相手プレイヤーは展開を続けるかどうかの選択を強いられ、そのジレンマに悩むことになります。増殖するGは非常に強力なカードのため、TCGフォーマットでは禁止、OCGでも24.10制限改訂で準制限に指定されました。この記事をご覧いただいているあなたなら、増殖するGを撃たれた時にどうプレイしますか?
手札誘発カードによる制約のメカニズムには、主に二つのタイプがあると考えられます。
ひとつは、物理的に相手の行動を制限するものです。
例えば、灰流うららは相手のサーチやドローなどの特定の効果を無効化し、展開の継続を直接妨害します。
このようなカードは、相手の動きそのものを封じ、次の行動を不可能にすることで、物理的な制約をもたらします。
もうひとつは、心理的な制約をかけるタイプです。増殖するGならびにOCGで最近実装された「マルチャミー」シリーズがその典型例で、相手の行動を「制約」するのではなく、「誘導」する効果を持っています。



相手はその後の展開を続ける選択肢が残されているものの、続けることで自分のリソースをリスクにさらすことになるため、展開の継続を躊躇せざるを得ません。
この心理的な制約は、相手プレイヤーに「進むか退くか」という決断を強制し、進むほどに不利な状況が構築される可能性が高まることから、独自の緊張感を生み出します。
特に、「その気になれば展開が可能であるにもかかわらず、相手にドローアドバンテージを与える」ことで、リソースを消耗させるジレンマは、他の手札誘発にはない心理的ストレスを引き起こすことが特徴です(図8)。

このように、増殖するGは物理的な制約に加えて、相手に戦略的な判断を迫る心理的な圧力をかける点で、他の手札誘発カードとは異なる独特な影響を与えます。
そのため、本稿では、物理的な妨害と心理的な圧力という二つの異なる制約が、プレイヤーに与えるストレスの度合いにどのように関わっているかを検討し、増殖するGが与える心理的影響について詳しく分析します。
問題提起と仮説
本稿の仮説は、『「増殖するG」がもたらす心理的影響が、他の手札誘発カードによる影響とは質的に異なる』、というものです。
一般的な手札誘発カードは、相手プレイヤーの行動を物理的に制約し、特定の展開を不可能にします。
例えば、「灰流うらら」や「エフェクト・ヴェーラー」は、相手の行動を直接的に妨害し、その先の展開を制限します。
しかし、「増殖するG」の場合、物理的な制約をかけるのではなく、プレイヤーに「続行するかどうか」の選択肢を与えます。
この選択肢の存在が、他の手札誘発とは異なる心理的なプレッシャーを生み出す要因となります。
具体的な仮説として、「増殖するG」はプレイヤーに対して、展開の自由を残しつつも、展開を続けることがリスクであると認識させ、その判断を強制することによって特有のストレスをもたらすと考えられます。
これは、物理的に展開を妨害されるのではなく、続行するほど相手にカードアドバンテージを与え、不利な状況に陥る可能性が高まるため、プレイヤーは展開を諦めざるを得ない状況に追い込まれるからです。
つまり、増殖するGは、展開を継続するか中止するかのジレンマを通じて、プレイヤーに異なるタイプのストレスをもたらします。
本稿の目的は、この仮説を検証し、「展開が可能であるが、続行するとリソース上の不利が生じる」という状況が、一般的な手札誘発によって展開が完全に止められる状況に比べて、プレイヤーにどの程度のストレスを引き起こすのかを明らかにすることです。
このストレスの原因を分析することで、プレイヤーの意思決定プロセスと、ゲームにおける心理的プレッシャーの違いを理解することができます。
また、本研究では、「展開の自由が残されている状況」と「物理的に展開が不可能となる状況」との間で、プレイヤーの反応やストレスレベルにどのような差が生じるのかを比較し、カードゲームにおける心理的影響の側面を明らかにします。
これにより、プレイヤーがゲーム中に抱える心理的負担の要因を特定し、増殖するGが与えるユニークな影響を解明することを目指します。
最終的に、これらの分析結果を基に、増殖するGのようなカードがプレイヤーに与える心理的影響が、プレイ体験全体にどのように影響するのかを明らかにすることが、本稿の目的です。
理論的フレームワークと心理学的視点の検討
本稿では、「増殖するG」がプレイヤーに与えるストレスの心理的影響を理解するために、複数の心理学的理論とゲーム理論の視点を導入します。
これにより、増殖するGの効果が単なるゲーム内の妨害手段としてではなく、プレイヤーの意思決定プロセスや心理的負荷にどのように影響を与えるかを包括的に分析します。
選択によるストレス
選択によるストレスは、複数の選択肢の中から最適な選択を迫られる状況で生じる心理的負担を指します。
遊戯王において「増殖するG」が発動された場合、プレイヤーは展開を続行するか中断するかの選択を強いられます。
この選択は、ゲームの進行状況やデッキの構築状況に大きく依存するため、プレイヤーは最適な判断を下すために高い認知的負荷を受けます。
選択の自由が存在する一方で、その選択がゲームの結果に直接的な影響を及ぼすため、プレイヤーはストレスを感じやすくなります。

不確実性による不安
不確実性による不安は、将来の結果が予測できない状況で生じる不安感を指します。
「増殖するG」の効果により、自分が特殊召喚を行うたびに相手がデッキからカードを引く、つまり有効札を引き込む可能性が増加するため、プレイヤーは相手の行動の結果を予測しづらくなります。
この不確実性は、プレイヤーに対して不安を引き起こし、意思決定における自信を揺るがす要因となります。
不確実性が高まることで、プレイヤーは心理的に不安定な状態に置かれ、ゲーム全体のパフォーマンスにも影響を与える可能性があります。
損失回避
損失回避は、損失を避けることが利益を追求することよりも強い動機となる心理的傾向を指します。
遊戯王において「増殖するG」が発動されると、プレイヤーはカードアドバンテージを相手に与えるリスクと、自身の展開を維持する利益との間でジレンマに直面します。
損失回避の観点から、プレイヤーはリスクを最小限に抑えようとするため、展開を中断する選択を優先する傾向があると考えられます。この心理的傾向は、プレイヤーが展開を諦めざるを得ない状況において、より強いストレスを感じる原因となります。

ゲーム理論による意思決定のジレンマ
ゲーム理論の視点から見ると、「増殖するG」の使用は、プレイヤーにとってリスクとリターンのバランスを考慮した戦略的意思決定を迫る要因となります。
特に、以下の2つの選択肢が存在します。
展開を続行する選択肢:
リスク:相手にカードアドバンテージを与える可能性が高まり、ゲーム全体の流れを不利にするリスクが伴います。
リターン:展開を続けることで、相手のプレッシャーを軽減し、自身の戦略を維持する機会を得ることができます。
展開を中断する選択肢:
リスク:自身の戦略を放棄することで、相手に対する優位性を失う可能性があります。
リターン:相手に対するカードアドバンテージの増加を防ぎ、自身のリソースを守ることができます。
このような状況下で、プレイヤーはリスクとリターンのバランスを慎重に評価し、最適な意思決定を下さなければなりません。
特に、「増殖するG」がもたらす継続的なプレッシャーは、プレイヤーに対して継続的な意思決定を強いるため、心理的負荷が蓄積されやすくなります。
ゲーム理論の観点からは、このような選択のジレンマがプレイヤーのストレスレベルを高める主要な要因であると考えられます。
総合的な分析
以上の心理学的視点とゲーム理論の分析を統合することで、「増殖するG」がプレイヤーに与えるストレスのメカニズムを明確に理解することが可能となります。
選択によるストレス、不確実性による不安、損失回避の心理的傾向、そしてゲーム理論に基づく意思決定のジレンマが相互に影響し合うことで、プレイヤーは高度な心理的負荷を経験します。
本研究では、これらの理論的枠組みを基に、実証的なデータを収集・分析し、「増殖するG」が他の手札誘発カードと比較してどのように異なる心理的影響を与えるのかを検証します。
調査方法とデータ収集
概要
本研究では、遊戯王プレイヤーの増殖するG使用後の心理的影響を測定するため、アンケートを実施します。
調査協力者は広くインターネット上で募集し、プレイヤーのゲーム中の経験やストレスレベルを測定する方法をとります。
シンプルかつ効率的なアンケートの構成を採用し、回答時間は3〜4分以内を目標とします。
アンケート調査の質問項目
増殖するG使用時の心理的反応
「増殖するG」が相手に使用された際の,「展開を続行するかどうか選択する」ことに対するストレス(先述の「選択によるストレス」視点より.)
この設問,ぴにき様の本来の疑問の意図「増殖するGが通ることで,『展開はその気になれば続行可能だが諦めざるを得ない状況』のストレス」とは若干ズレてしまっていることに後になってから気づきました.本当にすみません.既にアンケートは実施してしまったので,このまま分析します.
「増殖するG」が相手に使用された際の不安度(総合,盤面が貧弱になること,相手にアドバンテージを与えることの3視点の不安度)を1(全く不安を感じない)から5(非常に不安を感じる)の範囲で評価
ここでいう「不安」は、「未来の出来事、予測できない状況への恐れ(不確実性に対する心配)」と定義
展開の自由度と心理的影響
展開が物理的に制約される(例:灰流うらら,エフェクト・ヴェーラー,無限泡影による妨害)場合と比較し、不安,ストレスの違いを評価。
「増殖するG」が通った場合の選択肢の有無に対する心理的負荷の大きさを評価するため、仮説:「展開が可能であるが続行すると不利になる状況は、物理的に制約される状況に比べて、より大きなストレスを感じる」かどうかを評価。
自由記述欄
「増殖するG使用後に感じる心理的影響」「その他の手札誘発使用後に感じる心理的影響」について、自由に記述してもらう項目。
特に、展開を続けるかどうかの選択を迫られる状況での感じたストレスや決断の理由について記述することを期待します。
また、普段使用するデッキについても記述いただきます。使用するデッキによって、増殖するGを撃たれた際の反応は全く異なるからですね。
例:粛声、ふわんだりぃず、神碑、メタビートのようにそもそも増殖するGが刺さらないデッキ
例:天盃龍、FTK(先攻ワンキル)のように、増殖するGを撃たれたとしても関係なく展開してくるようなデッキ
分析方法
収集した定量データは、平均,分散,標準偏差等の基礎統計量を計算したのち,統計的仮説検定を用いて、増殖するGによるプレッシャーの度合いが他の手札誘発カードによるものと偶然ではない差があるかどうかを検証します。
さらに、5段階での評価項目については相関分析を行い、プレイヤーのストレスの相互関係を明らかにします。
加えて,因子分析を実施し,データの背景特性についても考察します.
補足:相関係数
相関係数とは、2つのデータの間にどれくらい関係があるかを表す数値のことです。例えば、「増殖するGが使われたときに感じるストレス」と「その他の手札誘発が使われたときに感じるストレス」が、どの程度関係しているかを調べるのに使います。相関係数は-1から1までの値で、1に近いほど「強く正の関係」があり、-1に近いほど「強く負の関係」があります。もし相関係数が0に近ければ、「ほとんど関係がない」という意味になります。
相関係数を計算するのは、アンケートの項目同士がどれくらい関係しているかを知りたいからです。たとえば、「増殖するGを使われたときのストレス」と「展開できないことに対する不安」「相手にアドバンテージを与える不安」が高い相関を持っている場合、それは「増殖するGがプレイヤーに与える心理的な影響」が強いことを示しているかもしれません。相関係数を使うことで、どの項目がプレイヤーにどれくらい影響を与えているかを分析し、より詳しく理解することができます。
ただし、相関係数は「相関関係」を示唆するものであって「因果関係」を示すものではない点に注意が必要です。
相関関係とは?
相関関係とは、「2つのものが一緒に変化する傾向がある」という意味です。つまり、ある要素が増えるともう一方も増える、あるいは片方が減るともう一方も減る、といった関係を指します。
例えば、「暑い日にアイスクリームの売り上げが増える」現象を考えてみましょう。この場合、気温が上がるほどアイスを買う人が増えるため、「気温」と「アイスの売り上げ」には相関関係があります。しかし、これが「アイスを買うと気温が上がる」という因果関係を示しているわけではありません。
因果関係とは?
一方で、因果関係とは、「1つのことが原因となって、もう1つのことが結果として起こる」という関係を意味します。先ほどの例で言えば、「暑いから人々がアイスを買う」というのは因果関係に当たります。この場合、「暑さ」が原因で「アイスの売り上げ」が増える結果が生じているのです。
相関関係と因果関係の違い
相関関係があるからといって、必ずしも因果関係があるとは限りません。むしろ、相関関係が見られる場合でも、以下のような状況が多く見られます:
共通の要因が存在する場合
例えば、「暑い日にアイスを買う人」と「プールに行く人」が増える場合、これらは「暑さ」という共通の原因によるものです。「アイスを買ったからプールに行った」という因果関係ではありません。偶然の相関
全く関連のない2つのデータでも、偶然相関が高く見える場合があります。因果の方向が不明確
例えば、「勉強時間が長い人ほどテストの点数が高い」という相関があった場合、「勉強したから点数が高い」のか、「点数が高い人が勉強もしている」のかは、このデータだけでは分かりません。
したがって、相関関係は、「2つのものが一緒に変化する」関係を示唆するものであり、因果関係を直接的に証明するものではありません。本研究でも、相関の解釈を慎重に行い、因果関係を示すものと誤解されないよう注意を払っています。データの解釈において、「相関=因果」ではないことを常に意識することが重要です。
相関係数のp値について
p値とは、相関が「たまたまではなく、本当に関係があるかどうか」を確認するための数値です。p値が0.05より小さいとき、「この相関は偶然ではない」とみなせます。つまり、p値が低いほど、2つのデータが実際に関連している可能性が高いと判断できるのです。たとえば、「増殖するGが使われたときのストレス」と「展開できない不安」の相関係数を計算し、p値が低ければ、これらが本当に関係していると考えます。
ただし、ここで注意が必要なのは、p値は「相関が0であるか否か」を判断するものに過ぎず、「相関の強さ」とは無関係であるという点です。したがって、p値が低いからといって相関があるかどうか判断するのは危険であるということです。
補足:統計的仮説検定
調査データを分析する際、仮説が「正しいか間違っているか」を統計的に判断するために仮説検定を行います。本研究では、増殖するGが他の手札誘発カードと比べて特異な心理的影響を与えるかを検証するために、2つの仮説検定手法を使用しました。それぞれの方法とその適用場面について解説します。
マン=ホイットニーのU検定
マン=ホイットニーのU検定は2つの独立したグループ間でデータの分布が異なるかを確認する方法です。この検定は、データが正規分布を仮定しない場合でも適用できるため、リッカート尺度のような順序尺度データの分析に適しています。
例えば、遊戯王OCGとMaster Duelのプレイヤーが、それぞれ「増殖するG」の効果に対してどの程度ストレスを感じるかを比較したい場合に利用します。これにより、両グループ間のストレスレベルに有意な違いがあるかを確認できます。
Wilcoxon符号付き順位検定
Wilcoxon符号付き順位検定は、同じ被験者や関連のあるデータペア間で順位の差が有意かどうかを調べる方法です。マン=ホイットニーのU検定とは異なり、この検定はデータがペアであることを前提とします。
本研究では、「増殖するGを使用された場合のストレス」と「その他の手札誘発を使用された場合のストレス」を比較する際にWilcoxon符号付き順位検定を使用しました。これは同じプレイヤーが異なる状況下で回答しているため、ペアデータとして扱えるからです。
これらの検定を採用した理由
本研究のデータは5段階での回答を用いた順序尺度データであり、平均値の比較に適したt検定などの方法ではなく、分布を直接比較できる検定が適切です。データの分布が正規分布を仮定できないため、これらの検定が有効です。
統計的仮説検定において「有意差がある」とは?
「有意差がある」というのは、あるデータに対して「偶然だけでは説明できない違いがある」という意味です。
統計的仮説検定では、「2つのグループに本当に違いがあるかどうか」を調べるときに、まず「違いはない」という仮説を立てます。そして、その仮説が正しいと仮定してデータを分析します。分析の結果、p値が出てきますが、これは「本当は違いがないときに、たまたま観察されたデータのような差が出る確率」を示しています。
例えば、p値が0.05であれば「5%の確率で偶然に同じような結果が出る」という意味です。一般的には、この境目を0.05や0.01とし、これを基準にします。p値がこの基準よりも小さいと、「偶然にここまでの違いが出る確率がとても低いから、違いがあると考えたほうが良さそうだ」と判断し、「有意差がある」と結論づけます。
つまり、p値がある境目を下回ることで、「データの違いは偶然ではなく、本当に異なる傾向がある」と示唆されるのです。
補足:因子分析
因子分析は、たくさんのデータの中に隠れている「共通の特徴」や「大きな流れ」を見つけ出すための方法です。平たく言えば、「アンケートをグループ分けする方法」ということです。
例えば,学校で生徒に5つの質問をしたとします:
勉強が好きですか?
宿題を毎日しますか?
先生の話をしっかり聞きますか?
スポーツが得意ですか?
運動部に入っていますか?
この5つの質問は、「勉強が得意かどうか」や「運動が得意かどうか」といった2つの大きな特徴(因子)に分けられるかもしれません。因子分析では、「たくさんの質問やデータ」をグループ分けして、「どんな特徴(因子)がデータを説明しているのか」を見つけ出します。
因子分析をすると、1つ1つの質問(項目)がどの因子に関係しているかがわかります。この関係の強さを「因子負荷量」といいます。これにより、たくさんの情報が「少ない数の特徴」にまとめられるのです。
この研究では、遊戯王OCGでカード「増殖するG」がプレイヤーに与える心理的影響について調べています。アンケートで得られたデータには、たくさんの項目(質問)が含まれていますが、それを因子分析で整理する理由は以下の通りです:
共通する特徴を見つけたいから
アンケートの回答には、「ストレス」や「不安」「選択の難しさ」など、心理的な特徴が複雑に絡み合っています。
因子分析を使うと、「これらの項目はストレスに関係している」「これらは不安に関係している」といった具合に、共通する特徴をまとめて整理することができます。
データをわかりやすくするため
質問がたくさんあると、それぞれを一つずつ分析するのは大変です。因子分析を使えば、たくさんの項目を少数の因子にまとめられます。
これにより、「増殖するGが特にどの心理的特徴に影響しているか」を簡潔に説明できるようになります。
増殖するGの特異性を明らかにするため
因子分析を通じて、増殖するGが他のカードとは異なる心理的影響(例えば「選択のストレス」や「リスク回避の不安」)を持つかどうかを確認できます。
特定の因子が増殖するGに特有のものであれば、「このカードが他のカードとどう違うのか」を明確に説明できます。
因子分析を使うことで、データの中に隠れている「増殖するGの心理的な特性」を見つけ出せるのです!
テキストマイニング
自由記述データに対しては、USERLOCAL社のテキストマイニング手法を活用し、キーワードの頻度分析を実施します。
テキストマイニングツール:
https://textmining.userlocal.jp/

USERLOCAL社のテキストマイニングは、文章データから単語の出現頻度や関連性、感情などを分析し、そこから有益な情報を見つけ出すためのツールです。このツールを使うと、例えば「どの言葉がよく出てくるか」「どんな言葉が一緒に使われているか」「文章全体の感情がどうか」といったことが分かります。
これにより、ストレスの原因や、プレイヤーが抱く共通の感情や不安についての理解を深められます。
視覚的な理解を容易にするために、結果はワードクラウドやネットワーク図などを用いて提示し、プレイヤーが特定の状況においてどのような心理的影響を受けるのかを具体的に把握します。
本調査のデザインにより、増殖するGによる心理的負担が他の手札誘発とどのように異なるのかについて分析できると考えます。
実験結果の分析と考察
お待たせしました.
ここからは実験結果を分析していきます.
皆さんのご協力のおかげで,104件もアンケートにご回答いただけました(n=104).
アンケートにご協力いただいた皆さん,本当にありがとうございました.
アンケート調査結果
ここでは,端的にアンケート調査の結果のあらましを列挙します.


※分布数1のデッキ








上記のグラフをもとにした考察を以下に示します。
デッキ分布に関する考察(アンケート調査より)
図13に,今回集計したデッキ分布を示しています.
分布トップは以下でした.
インフェルノイド
ティアラメンツ(マナドゥムティアラや40ティアラも今回「ティアラメンツ」で統一しました)
ライゼオル
天盃龍
センチュリオン(永続型は派生系のひとつであって大元は「センチュリオン」なので統一しています.)
どれも環境で一定の存在感を持つデッキばかりだと思います.
天盃はゴリゴリの後手特化ビートダウンデッキでGはそれほどキツくないですが,それ以外の顔ぶれは展開またはミッドレンジ系のデッキで,Gはそこそこキツいデッキだと思います.
また,これらに次いで多かったのは
粛声
ふわんだりぃず
ユベル
でした.いずれもミッドレンジ系のデッキですが,粛声もふわんだりぃずも増殖するGをほぼ喰らわないデッキであり,増殖するGを喰らわないデッキをよく使う人の回答割合が相対的に多かった点は特筆すべき点であると思います.
今回はデッキごとの詳細な分析は実施しませんが,今後追加でアンケートを実施する際は,デッキの具体名だけでなく,デッキのタイプや増殖するGの受けの良さも考慮して分析を実施したいですね.
ストレスに関する考察(アンケート調査より)
「増殖するG」によって選択を迫られたときのストレス
図14のグラフでは、「増殖するG」を使われたときのストレスの感じ方が多様であり、特に「4」や「5」といった高いストレスレベルの回答が多いものの、「3」やそれ以下のストレスレベルも一定数存在します。この分布から、「選択によるストレス」はプレイヤーによって感じ方が異なることが示唆されます(Gの受けがいいデッキと悪いデッキがあるため)。選択によるストレスは、プレイヤーが「展開するか否かの選択」に迷うことで生じるため、「失敗するかもしれない不安」や「相手にカードを引かせたくない心理的な負担」が要因と考えられます。
展開が物理的に制限されたときのストレス
図19のグラフを見ると、ストレスの度合いが「4」や「5」の回答が多く、全体の約半数(約52.9%)が「強いストレス」を感じていることがわかります。これにより、多くのプレイヤーが展開がそもそも続行不可能になったときに高いストレスを感じる傾向があるといえます。物理的な制約によるストレスは、「やりたいことが完全にできなくなった」という感情が引き起こすものであり、強い不快感やフラストレーションに繋がりやすいようです。
ストレスに関する考察まとめ
「増殖するG」による選択のストレスは、プレイヤーごとにばらつきがあり,これはおそらくプレイヤーの使用デッキの差に起因すると予想されます.
一方で,物理的制約によるストレスは比較的一貫して「高い」傾向にあり、明確にプレイヤーにストレスを与えています。
不安度合いに関する考察(アンケート調査より)
アンケート調査結果から、増殖するGと他の手札誘発がプレイヤーに与える不安度合いの違いを考察します。
増殖するGの総合的な不安度
図15のグラフに示されている通り、約64.5%(「4」または「5」を選んだ割合)のプレイヤーが、「増殖するG」に対して強い不安を感じていることがわかります。この不安は「未来の予測ができない」という要素から生じています。つまり、「増殖するG」によって相手が新しいカードを引くことで、自分の展開が阻害される可能性があると予測できない状況が不安の原因となっています。
増殖するGによって「相手にアドバンテージを与える」不安
図16のグラフでは、52.9%が「5」を選択し、非常に高い不安を感じています。特に、「自分の展開を進めることで相手がカードを増やしてしまう」リスクが心理的な負担となっていることが示されています。この不安は、プレイヤーが「展開を進めるかどうか」を選択する際の重大な懸念材料です。
増殖するGによって「十分な盤面を作れない」不安
図17のグラフでは、約61.6%(「4」または「5」)が「十分な盤面を作れない」ことに対する不安を感じていると回答しています。これは、増殖するGによって相手の手札が増えることで、強力な展開が抑制される可能性があることへの懸念を示しています。この不安は、「理想の盤面を構築できるか」という期待と現実のギャップが生む心理的負担です。
他の手札誘発による不安
図20のグラフでは、他の手札誘発(例えば、灰流うららや無限泡影など)に対して、不安が平均的に広がっていることが示されています。これらのカードが「物理的に展開を妨害する」特性を持つため、プレイヤーが感じる不安は「展開できない」というシンプルな制約に基づいており、増殖するGのような「選択に伴う不安」や「相手にアドバンテージを与える不安」とは異なる心理的影響を与えています。
不安度合いに関する考察まとめ
増殖するGに対しては、過半数のプレイヤーが非常に強く不安を感じ,なおかつ「十分な盤面を作れない不安」よりも「相手にアドバンテージを与える不安」が上回っています.これは,先ほどご説明した「不確実性による不安」理論とも合致します.
一方、他の手札誘発は、不安が平均的に広がっており,増殖するGを撃たれた際に見られる「選択に伴う不安」「相手にアドバンテージを与える不安」とは異なる心理的影響を与えることが示唆されます.
これらの違いは、次に行う相関分析やWilcoxon符号付き順位検定、因子分析を通じて、より具体的に確認し、心理的影響の違いを数値的に裏付けることが期待されます。
リスク回避に関する考察
概要
図18を見ると、「増殖するG」を相手に使用された際、プレイヤーがリスクを避けたいと強く感じていることが分かります。特に「5」を選んだ回答が52.9%を占めており、半数以上のプレイヤーが非常に強いリスク回避の意識を抱いていることが示されています。また、「4」と合わせると約76.9%のプレイヤーが「リスク回避」を強く意識していることが確認できます。
リスク回避の心理的背景
「増殖するG」を撃たれたとき、プレイヤーは「展開を続けることで相手にアドバンテージを与えてしまう」というリスクを考慮しなければならなくなります。このリスクを避けるため、展開を控えたり中断する選択をするプレイヤーが多く、心理的に「展開し続けることで失う可能性」に対する恐れが高まっています。
この結果の意味
この高いリスク回避の意識は、プレイヤーが「増殖するG」に対して強い心理的負担を感じていることを示唆します。「選択する自由」があるにもかかわらず、その選択が不利な状況を引き起こすリスクと向き合わざるを得ないため、プレイヤーは心理的な葛藤を感じています。
基礎統計量
また,以下に計算した基礎統計量を示します.
※プログラミングの都合上,設問名を短縮しています.
Gストレス総合:Gを撃たれるストレス
G不安総合:Gを撃たれる総合的な不安
G不安アド:Gを撃たれる,「アドバンテージを与える」不安
G不安貧弱盤面:Gを撃たれる,「十分に展開できない」不安
Gリスク:Gを撃たれる,「リスクを避けたいという気持ち」
その他ストレス:G以外を撃たれた際のストレス
その他不安:G以外を撃たれた際の不安

基礎統計量の考察
表2は、各設問に対する平均値、中央値、最頻値、分散、標準偏差といった基礎統計量を示しており、「増殖するG」およびその他の手札誘発カードがプレイヤーに与える心理的影響を数値的に表しています。
1. G不安アド(アドバンテージを与える不安)
平均値: 4.2115と高く、プレイヤーの大半がこの不安を強く感じていることを示しています。
中央値と最頻値: 両方とも5であり、プレイヤーが「非常に不安」と回答する傾向が強いことを反映しています。
分散と標準偏差: 1.0616と1.0303で、他の項目と比較して変動が小さく、ほぼ全員が同様の不安を感じていることを示唆しています。
2. Gリスク(リスクを避けたい気持ち)
平均値: 4.1635と高く、リスク回避の意識が強いことを示しています。
中央値と最頻値: 両方とも5で、「非常に強くリスクを避けたい」と感じているプレイヤーが多いことがわかります。
分散と標準偏差: 1.2254と1.107で、やや個人差はあるものの、リスク回避の傾向は一貫しています。
3. G不安貧弱盤面(十分に展開できない不安)
平均値: 3.7115とやや高めですが、G不安アドやGリスクに比べると低めです。
中央値と最頻値: 4と5で、多くのプレイヤーが一定の不安を感じているものの、リスクやアドバンテージの不安ほどではありません。
分散と標準偏差: 1.5665と1.2516で、回答に若干のばらつきが見られます。
4. Gストレス総合(Gを撃たれるストレス)
平均値: 3.5とやや中間的な値で、他の項目よりもストレスの感じ方が弱いことがわかります。
中央値と最頻値: 4と5であり、プレイヤーの多くはある程度のストレスを感じているようです。
分散と標準偏差: 1.6699と1.2922で、他の項目と比べて回答のばらつきがやや大きいです。
5. その他ストレスおよびその他不安
その他ストレス: 平均値3.6154、中央値4と、増殖するG以外の手札誘発にも一定のストレスがあるものの、Gストレス総合と近い値です。
その他不安: 平均値3.25と低めで、Gを撃たれたときの不安に比べて総合的な不安度が低いことを示しています。中央値も3で、プレイヤーが増殖するG以外の手札誘発に対して、より少ない不安を感じていることがわかります。
総合的な考察(基礎統計量より)
「増殖するG」がプレイヤーに与える心理的影響として、特に「アドバンテージを与える不安」や「リスクを避けたい気持ち」が強く感じられていることがわかります。これは、単に「物理的に展開を妨害される」よりも「自分の選択が相手に有利になる可能性を伴う」ことが、心理的なプレッシャーとして作用していることを示唆します。
その他の手札誘発カードに対する不安やストレスは、増殖するGに比べると低めであり、増殖するGが特異的な心理的負担を引き起こしていることがわかります。
相関係数とP値


相関係数とp値の考察
相関係数の結果
Gストレス総合と他のG関連項目の相関
G不安総合(相関係数 0.49)やG不安アド(相関係数 0.44)、G不安貧弱盤面(相関係数 0.52)と微弱な相関を示しており、これらの項目が関連している可能性があることがわかります。
これにより、「増殖するG」によるストレスは総合的な不安や「アドバンテージを与える不安」、および「十分に展開できない不安」と微弱な相関を示しており、ある程度の関連性がある可能性があります。
Gリスクと他のG関連項目の相関
G不安アド(相関係数 0.39)やG不安貧弱盤面(相関係数 0.29)と微弱な相関を示しています。
この結果から、「リスクを避けたい気持ち」が、プレイヤーが感じる他の不安と一定の関連を持っている可能性が示唆されます。ただし、Gストレス総合ほどの強い結びつきは見られず、独自の心理的な影響があると考えられます。
その他ストレスとその他不安の高い相関
その他ストレスとその他不安の間にはやや高い相関(相関係数 0.74)が見られ、G以外の手札誘発に対するストレスと不安が比較的強く結びついていることがわかります。これにより、G以外の手札誘発が、プレイヤーに一貫した心理的影響を与えていることが確認できます。
相関係数のp値の結果
p値が高い組み合わせが多く、この相関が偶然である可能性が示唆されています(一般的にP < 0.05やP<0.01で有意とされます)。
一方で、GリスクとGストレス総合のp値(0.0001)や、G不安貧弱盤面とGストレス総合のp値(0.0032)は非常に低く、偶然でない相関が確認されています。
これにより、特定の不安やリスクが増殖するGに関連してプレイヤーの心理的負担として影響していると推察されます。
総合的な考察(相関係数とp値より)
G関連の項目(ストレス、不安、リスク)は、相互に関係が強く、特にGによるストレスが複数の不安要因と結びついていることが示されています。
他方で、その他の誘発によるストレスと不安はG関連とは独立した相関を示しており、Gによる影響がプレイヤーに特異な心理的負担を与えていることが浮き彫りになっています。
マン=ホイットニーのU検定の結果

マン=ホイットニーのU検定の考察
表4は、マスターデュエル(MD)とOCGの2つの群間で各項目のスコアに有意差があるかどうかを検証するため、マン=ホイットニーのU検定を実施した結果です。U統計量とそのp値が示されています。以下に、各項目について考察します。
全体として、どの項目もP値が0.05を大きく上回っているため、MDとOCGの間で「増殖するG」やその他の手札誘発カードに対するストレスや不安の感じ方に差はないと結論づけられます。この結果は、MD・OCGどちらの群でも「増殖するG」による心理的負担が類似していることを示唆しており、「増殖するG」がフォーマット問わず「遊戯王」のゲームプレイ全般において一貫した心理的影響を及ぼしている可能性が考えられます。
Wilcoxon符号付き順位検定の結果
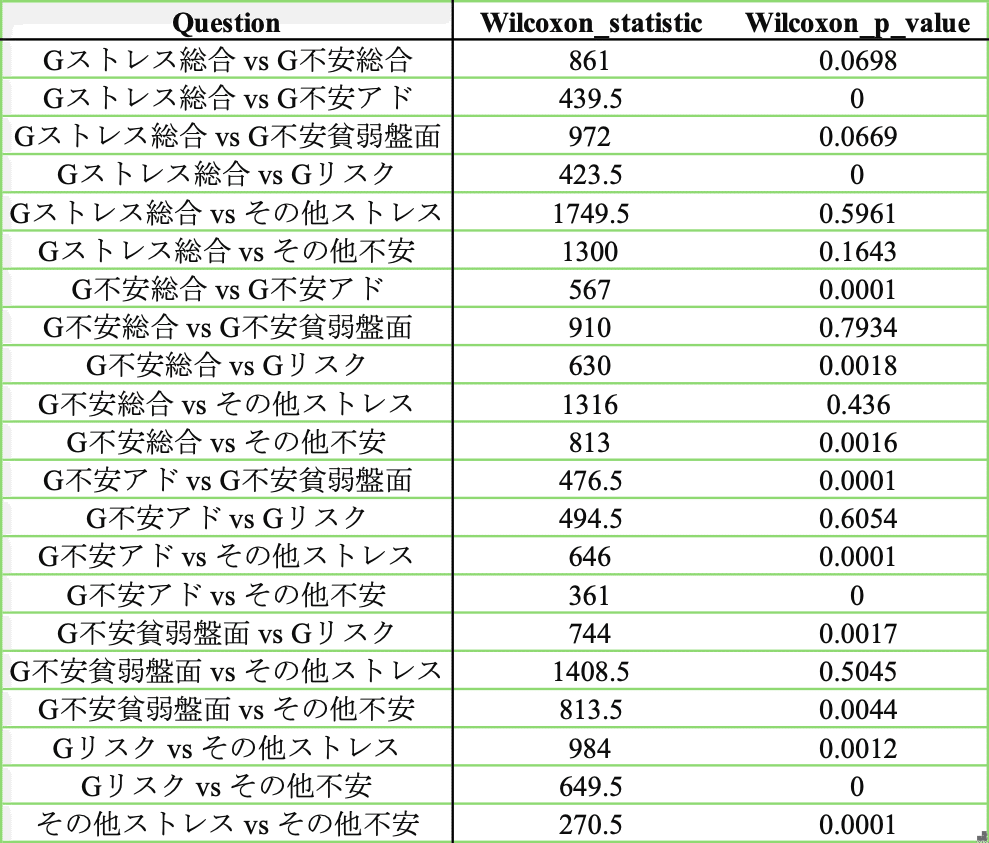
表5は、五段階評価で質問した各項目間でWilcoxon符号付き順位検定を実施した結果で、統計量(Wilcoxon_statistic)とp値(Wilcoxon_p_value)が示されています。この検定は、対応する2つの項目の間に有意な差があるかどうかを確認するために行われました。以下に、主な項目の結果とその意味を解説します。
Wilcoxon符号付き順位検定結果の概要
まず,最も明らかにしたかった部分である,「Gストレス総合(Gを撃たれる総合的なストレス)」と「その他ストレス(その他の手札誘発を撃たれるストレス)」の間には偶然ではない差が認められませんでした(P値 = 0.5961)。これは、「増殖するG」によるストレスと、他の手札誘発カードによって物理的に展開が妨害されたときのストレスが、参加者にとってはおおむね同様の心理的負担として感じられている可能性を示唆しています。
「Gストレス総合」と「その他ストレス」の有意差が無かった件に関する考察
共通する「ストレス」の要因
増殖するGと他の手札誘発カードはどちらもプレイヤーの展開に対して直接的な妨害効果を持つため、プレイヤーがゲームを進める上での計画を強制的に変更させられる点では共通しています。この「計画を阻まれる」点が共通のストレス要因となっており、結果的に「Gストレス」と「その他ストレス」の違いが少なく感じられたと考えられます。
「ストレス」と「不安」の違い
ここで注意すべきは、「ストレス」と「不安」が異なる心理的負担である点です。ストレスは外部からの圧力や負荷によって生じる一時的な緊張感や不快感を指し、一方で不安は「先の見えない状況への心配や懸念」といった、より持続的な心理的負担に近いものです。このため、増殖するGと他の手札誘発の「ストレス」に違いが見られなかったのは、どちらのケースでも外部からの直接的な妨害という点がプレイヤーに同様の影響を与えているためと考えられます。
選択を迫られる「不安」との対比
一方で、増殖するGには「相手にアドバンテージを与えるか、自分の展開を中断するか」という選択が伴い、これが特有の「不安」や「リスク回避意識」に結びついています。しかし、ストレスに関しては「どちらも計画が妨害された結果」として同じように受け取られた可能性が高いです(これに関しては私の質問の仕方も良くなかったかもしれません)。したがって、ストレスレベルにおいては増殖するGと他の手札誘発カードで有意差が出なかったものの、後述の通り不安レベルでは大きな差が認められたということは、増殖するGがプレイヤーに特有の心理的負担を与えるカードであることを強く示唆しています。
その他の部分の考察(Wilcoxon符号付き順位検定結果より)
Gストレス総合に関連する項目
Gストレス総合 vs G不安アド(P値 = 0.0)および Gストレス総合 vs Gリスク(P値 = 0.0)で偶然ではない差が認められました。
これにより、Gストレス総合が、特に「アドバンテージを与えることに対する不安」や「リスクを避けたい気持ち」と異なる特徴を持つことが示されています。つまり、総合的なストレスの感じ方と具体的な不安やリスク回避意識には顕著な違いがあると考えられます。
Gストレス総合 vs G不安貧弱盤面(P値 = 0.0669)
ここでは有意水準には達していませんが、近似値であり、「展開が十分にできないことへの不安」と総合的なストレスの間に若干の違いがあることを示唆しています。
G不安総合に関連する項目
G不安総合 vs G不安アド(P値 = 0.0001)および G不安総合 vs Gリスク(P値 = 0.0018)で有意差が見られます。
これらの結果は、総合的な不安と具体的なアドバンテージやリスクの不安が異なる心理的な影響を与えていることを示しています。総合的な不安は、特定の状況に焦点を当てた不安とは異なる捉え方がされている可能性があります。
G不安総合 vs G不安貧弱盤面(P値 = 0.7934)
この組み合わせでは有意差が見られず、「展開不足による不安」と総合的な不安は似たような心理的影響を与えていると考えられます。
G不安アド(アドバンテージを与える不安)に関連する項目
G不安アド vs その他ストレス(P値 = 0.0)および G不安アド vs その他不安(P値 = 0.0)で有意差が見られます。
「アドバンテージを与えることに対する不安」が、G以外の手札誘発カードによるストレスや不安とは異なる心理的負担をもたらしていることが明示されています。この結果は、「増殖するG」が特定の種類の心理的負担を引き起こすカードであることを示唆します。
G不安貧弱盤面に関連する項目
G不安貧弱盤面 vs その他不安(P値 = 0.0044)で有意差が確認されました。
「展開不足による不安」と「G以外のカードによる不安」の間に明確な違いがあり、特に「増殖するG」が引き起こす心理的影響は他の手札誘発カードとは異なる側面があることが示されています。
Gリスクに関連する項目
Gリスク vs その他ストレス(P値 = 0.0012)および Gリスク vs その他不安(P値 = 0.0)で有意差が確認されました。
リスクを避けたい気持ちは、G以外のカードによるストレスや不安とは異なる心理的影響を持つと考えられます。特に、「増殖するG」がプレイヤーに与えるリスク回避の意識は、他の手札誘発カードよりも強力である可能性があります。
総合的な考察(統計的仮説検定より)
これらの結果から、「増殖するG」は他の手札誘発カードに比べ、特有の心理的な影響を与えていることが示唆されます。特に、「アドバンテージを与える不安」「リスクを避けたい気持ち」が、G以外のカードの影響とは異なる傾向が見られます。このことは、「増殖するG」の存在がプレイヤーに対して選択を迫り、その選択によって生じる心理的な負担が強く作用していることを反映しています。
因子分析の事前調査結果
因子分析の妥当性やパラメータを判断するために事前調査を実施しました。
KMO Test:0.7015
KMOテストは、因子分析を実施する前に、データが因子分析に適しているかどうかを確認するために使います。このテストの値は 0 から 1 の間で、値が高いほど因子分析に適したデータであることを示します。
KMO > 0.9: 優れた因子分析に適している
0.8 < KMO < 0.9: 良い
0.7 < KMO < 0.8: まあまあ良い
0.6 < KMO < 0.7: 因子分析を行うには限界がある
KMO < 0.6: 因子分析には不適切
KMO = 0.7015は「まあまあ良い」というレベルで、因子分析を行うには問題ないと判断できます。しかし、理想的には 0.8 以上が望ましいです。この結果は因子分析に進んでも大丈夫な範囲ですが、ややギリギリな感じです。
Bartlett's Test: chi-square = 220.0, p-value = 0.000
Bartlettの球面性検定は、因子分析に進む前に、変数間に相関があるかを確認するために行います。テストの帰無仮説(否定したい仮説)は「変数間に相関がない」というものです。
p-value < 0.05: 有意であり、変数間に相関があり、因子分析が適している。
p-value ≥ 0.05: 有意ではなく、因子分析に適していない可能性がある。
今回,p-value が 0.05 より小さいため、有意であり、変数間に相関があることが確認されました。この結果は因子分析を実施するにあたり適切なデータであることを示しています。
したがって,今回のデータに対して因子分析を実施してもおおむね問題はないとみなせます。
固有値プロット(因子数の決定)

図22は因子分析における固有値プロット(スクリープロット)を示しています。横軸が「因子の数」、縦軸が「固有値」を表しており、固有値が減少していく様子を視覚化しています。このプロットを用いて、因子分析における適切な因子の数を決定します。
固有値プロットでは、いくつの因子を残すべきかを以下の基準で判断します:
カイザーの基準(固有値 > 1)
固有値が1以上の因子を選びます。
図を見ると、固有値が1を超えているのは2つの因子までです。この基準では、「因子数を2つ」とするのが妥当です。
スクリーテスト
「急激な減少が緩やかになる点(エルボー)」を探します。エルボーの前までの因子が重要であると判断します。
図22では、因子数が3の後で減少が緩やかになっています。この基準では、3つの因子を選ぶのが適切です。
上記の基準に加えて、研究目的に沿った因子数を選択します。研究で使う項目数や因子がどの程度心理的構造を説明できるかを考慮します。
本研究では、「増殖するGが特異な心理的影響を与えるか」を明らかにすることが目的です。そのため、因子数が少なすぎると特異性の解釈が困難になるリスクがあります。
したがって,今回は因子数3を選択します.
因子分析の実行結果
因子負荷量を以下の表6に示します.

また,因子得点をデッキ名と一緒に3次元・1次元にプロットした結果を以下に示します.(文字が小さくなりすぎたので,拡大してご覧ください。また、pngだと文字がつぶれてしまうのでpdfに変換しています。)
図23.因子得点の3次元プロット
図24.因子1の1次元プロット
図25.因子2の1次元プロット
図26.因子3の1次元プロット
因子分析の考察
表6について考察します.
そもそも因子負荷量とは、それぞれの設問項目が特定の因子(特徴)にどれだけ関連しているかを示す数値です。
数値が大きいほど、その設問がその因子に強く関係していることを意味します。負荷量が「0.4以上」であれば、その因子と関連が強いとみなされることが一般的です。負荷量が負の値であれば、因子とは逆の関係を示しています。
因子1
Gストレス総合,G不安総合,G不安アド,G不安貧弱盤面の4項目において負荷量が0.4を超えています.これより,因子1は増殖するGに対する不安・ストレスと関連が強いとみなせます.
実際,図24を確認すると,「魔術師」「ライゼオル」「@イグニスター」のような増殖するGの受けが比較的悪めのデッキを回答したサンプルが高いスコアで,逆に「粛声」「クシャトリラ」のような比較的増殖するGの受けがよいデッキを回答したサンプルが低いスコアを示していることから,因子1が増殖するGに対する不安・ストレスと関係していると予想されます。
因子2
その他ストレス,その他不安の項目で負荷量が0.8オーバーとなっており,因子2はその他の手札誘発に対する不安・ストレスと関連が強いとみなせます.
図25を確認すると,「粛声」「ふわんだりぃず」のような誘発受けがあまり良くないデッキを回答したサンプルが高スコア(ただし粛声は1個スコアが低いサンプルもありました)で,逆に「天盃龍」や「メメント」のように比較的誘発受けが良い方のデッキが低スコアであったことから因子2がその他の手札誘発に対する不安・ストレスと関連が強い可能性があります
因子3
Gリスクが0.9オーバーであり,因子3はGを受けて展開するリスクに対する考え方と関連が強いとみなせます.
図26を確認すると,「粛声」「インフェルノイド」「烙印」のように,「その気になればG相手にツッパって展開ができる」デッキを回答したサンプルが高スコアで,逆に「天盃龍」「ラビュリンス」のようにそもそもGが重くないか,Gを食らってもツッパして展開できるようなデッキを回答したサンプルが低スコアだったことから,因子3がGを受けて展開するリスクと関連が強い可能性があります。
総括
これらの因子分析の結果は、増殖するGがプレイヤーに与える心理的影響を以下の3つの側面で分解して理解する手がかりを提供しました。
増殖するGにより引き起こされる不安・ストレスの全般的な影響(因子1)
増殖するGが「受けが悪いデッキ」や「脆弱な盤面」で特に心理的負担を生じさせていることが明確になりました。その他の誘発カードによる心理的影響(因子2)
増殖するG以外の手札誘発が与える不安・ストレスが独立して存在し、デッキ選択に影響を及ぼしていることが確認されました。展開リスクへの意識(因子3)
増殖するGを受けながら展開を続けるリスクが、デッキごとのプレイスタイルに応じて異なることが示されました。
これらの結果は、増殖するGが他の手札誘発カードと比較して多層的な心理的影響を持つことを示唆しています。特に、増殖するGが単なる「相手ターンでのドロー誘発」にとどまらず、プレイヤーの戦術的判断やリスク許容度に直接的に影響を与える特異性を持つことが明らかになりました。
ただ,これらの考察には反例も多いです.
例えば,因子1では-1付近に覇王魔術師がいますし,因子2では先述の通り下から2番目になぜか粛声がいるので,この結果だけを見て「この因子と関連している」と断定するのは危険でしょう.
追加で分析が必要な部分だと思います.
しかしながら今回,「増殖するGへの受けの良さ・悪さ」の設問を設置していないにもかかわらず,このような明瞭な結果が出せたのは因子分析の成果だと思います(指摘してくれたalknightくんマジでありがとうございます)
テキストマイニング
「Gを撃たれた際のストレス」の自由記述部分のワードクラウド

「Gを撃たれた際のストレス」の自由記述部分の単語出現頻度

このワードクラウドと単語頻度分析から、「増殖するG」に対するプレイヤーのストレスの主要な要因が浮き彫りになっています。以下に考察を示します。
頻出語の分析
「手札」「誘発」「妨害」:これらの単語が最頻出単語でした.アンケート本文を目視で確認した結果,
増殖するGによって相手に別の誘発を引き込まれることによるストレス
こちらが先攻で作る妨害数よりも相手の手札が増えることによるストレス
Gを撃たれた際に,誘発が引けず展開の止めどころを失うストレス
などの複数種類のストレスを人それぞれ抱えているのが散見されました.
この例より,ひとくちに「増殖するGを撃たれるストレス」といっても複数の評価点があるとわかりました.
「G」「増殖」「ドロー」:「増殖」と「G」はいうまでもなく「増殖するG」のカード名を参照するものですが,「ドロー」の単語も比較的出現頻度が高かったです.これは効果により相手がドローを重ね、プレイヤーが相手にアドバンテージを与えてしまう状況が強いストレスの要因であることが示唆されています。実際アンケート本文を確認しても,捲り札や手札誘発を追加でドローされるリスクがあることに対するストレスが目立ちました.ドローが目立つことは、ドロー枚数が増えることによる相手の盤面強化がプレイヤーの心理的負担となっていることを示していると考えてよいでしょう。
「盤面」「展開」「特殊召喚」:これらは、プレイヤーの展開に対する制約がストレスの源であることを表しています。増殖するGを撃たれると、特殊召喚を繰り返すことで相手にカードを引かせるか、展開を控えるかの選択を迫られることがストレスに繋がっています。アンケート本文を見ても,最大展開できる手札なのに自らそれを諦めなければならないことに対するストレスが強調されていました.
心理的な圧迫感
「辛い」「不快」「怖い」といった感情表現が見られることから、増殖するGの効果が単なるゲーム内の妨害にとどまらず、プレイヤーにとって心理的な圧迫感や恐怖心を生むことが示唆されています。これにより、単なる妨害以上の負担がかかっていることが確認できます。アンケート本文からもそれが確認できました.
ストレスの多様な側面
「先攻」「構える」「ターン」「チェーン」などの単語は、戦略的なタイミングや構築を考慮しなければならないプレイヤーの状況を示しています。増殖するGはその他多数の手札誘発とは異なりフリーチェーン(自由なタイミングで発動できる)であるため,その発動タイミングに関しても駆け引きが存在するのが大きな特徴です.増殖するGが相手のターンで発動されることで、プレイヤーは戦略やターンごとの動きを慎重に考える必要があり、これがストレスの一因となっているようです。
まとめ
増殖するGによるストレスは、プレイヤーの展開に対する直接的な制約だけでなく、相手にドローを許すことでのアドバンテージの増加、そして選択を迫られる心理的なジレンマが重なることで、複合的なストレスが生じていることが示唆されます。
「その他の手札誘発を撃たれた際のストレス」の自由記述部分のワードクラウド

「その他の手札誘発を撃たれた際のストレス」の自由記述部分の単語出現頻度

上のワードクラウドと単語出現頻度から、増殖するG以外の手札誘発カードに対してプレイヤーが抱くストレスの要因が見えてきます。以下にその要因を分析し、考察を示します。
頻出語の分析
「誘発」「手札」「妨害」:増殖するG以外の手札誘発でも、やはり「手札誘発カード」による妨害がストレスの中心にあることが分かります。これは、プレイヤーが想定した展開が妨害されることで、自分の計画が破綻することに対する不満やストレスを反映しています。
「うらら」「ガンマ」「泡」:これらのカード名が目立っており、具体的にどの手札誘発カードがストレスの原因となっているかが示されています。特に即時の妨害能力を持つカードに対して、プレイヤーはストレスを感じていることがわかります。
プレイヤーの展開に対する影響
「初動」「展開」「リソース」:これらの言葉から、手札誘発による妨害がプレイヤーの初動や展開に大きな影響を与えていることが伺えます。初動を止められることは、そのターンの計画がほぼ無意味になることを意味し、結果的にリソースの浪費につながります。プレイヤーは、リソースの管理や戦略的な展開を大切にしているため、これが妨害されることに強いストレスを感じているといえます。
ストレスの多様な側面
「無理」:この言葉は、増殖するG以外の手札誘発がプレイヤーに精神的な負担や「諦め」に近い感情をもたらしていることを示しています。アンケート本文であった意見のひとつに,「増殖するGはあくまで選択肢(展開するかどうか)がこちらにある一方で手札誘発はその選択肢すら奪う」というご指摘があり,確かにその通りであると感じました.特に、手札誘発による妨害が続くと、相手の行動を阻止することが難しくなり、戦局が不利になると感じていることがわかります。
「受け入れがたい」:この言葉は、手札誘発による妨害が理不尽に感じられることを表しています。プレイヤーは戦略を練ってデッキを構築し、手札を選び取っているのに、それが簡単に無効化されることで、ゲームの流れに対するフラストレーションが溜まっていることが示唆されます。アンケート本文でも,「0妨害で番を返すのは受け入れがたい」という意見がありました.
まとめ
増殖するGと同様、その他の手札誘発もプレイヤーに対して強いストレスを引き起こしていることが確認できます。しかし、増殖するGと異なり、他の手札誘発カードは展開自体を物理的に阻止する性質が強く、それにより「諦め」や「無力感」がより顕著に現れています。この違いは、増殖するGが選択を迫る心理的負担を強調しているのに対し、その他の手札誘発が物理的な展開妨害と、それに伴う直接的なフラストレーションを生じさせている点にあると考えられます。
自由なご意見のワードクラウド

自由なご意見の単語出現頻度

図25,26のワードクラウドと単語出現頻度は、完全に自由記述の回答欄から得られたものであり、プレイヤーが「増殖するG」やその他の手札誘発カードに対するストレスや感じたことについて自由に意見を述べた結果です。以下に、主要な特徴とそこからの考察を示します。
頻出語の分析
「誘発」「手札」「増殖」「アトラクター」「マルチャミー」:これらの単語が中心付近に位置しており、増殖するGを始めとした手札誘発カードの影響に対して、プレイヤーが強く関心を持っていることがわかります。特に,増殖するGと同様にドローソースになる「マルチャミー」や,無限妨害になり多くのデッキでターンスキップできるだけの破壊力を持つ「アトラクター」など、特定のカード名が強調されていることから、プレイヤーにとってこれらのカードが戦術や戦略において重要な要素であると考えられます。
「ロンギヌス」「ヴェーラー」:特定の手札誘発カード名が頻出していることは、これらのカードが「増殖するG」と同じように、プレイヤーにとって困難な妨害要素として認識されていることを示唆しています。特に,ロンギヌスはデッキによっては機能停止に追いこまれる無限妨害のため,ロンギヌスに対しストレスを感じるプレイヤーは一定数存在すると考えられます.
プレイヤーの戦略に対する影響
「やり返す」「手数」「先攻」「引き込む」:これらの言葉から、プレイヤーが手札誘発や増殖するGに対抗するための手段や戦略に対しても強い関心を抱いていることが見て取れます。特に「やり返す」という単語があることから、妨害を受けたときにどう反撃するか、または妨害されないための戦術をどのように工夫するかが重要なテーマとなっていることが伺えます。
心理的・感情的な影響
「負荷」「辛い」:これらの言葉は、増殖するGや手札誘発カードがプレイヤーに心理的な負担をかけることを表しています。こういったネガティブな感情が示されていることから、妨害を受けたときに感じるストレスやフラストレーションが強いことがわかります。アンケート本文においても,「増殖するGを撃たれていない場合であっても存在を意識するだけで心理的負荷を感じる」といった意見がありました.
コミュニティや共感の表現
「遊戯王」「md」「アンケート」「ありがとう」:これらの単語から、回答したプレイヤーがコミュニティの一員としての意識を持っていることや、アンケートに参加することで自身の経験や意見が共有され、他者と共感できる場が提供されていることに対して感謝を感じていることが伺えます。
まとめ
この自由記述欄のワードクラウドからは、プレイヤーが手札誘発カードによる妨害を受けることで、戦術的な調整や心理的な負担を感じている様子がわかります。完全に自由記述のデータは、プレイヤーの生の声を反映しており、量的データでは得られない深い洞察を提供しているとみなせるでしょう。
本調査の結論
長くなるので、理論的結論と実験結果からの結論の2セクションに分けて述べます。
理論的な結論: 「増殖するGが心理的圧力を与える理由」
「増殖するG」は、他の手札誘発カードと異なり、プレイヤーに対して「展開を継続するか中断するか」の選択を迫る点で心理的な圧力を生み出します。この圧力の理由は以下の通りです。
選択のストレス
「増殖するG」の発動後、プレイヤーは行動の自由をある程度保持しているものの、どちらの選択肢にもリスクが伴います。特に「相手にカードアドバンテージを与えるリスク」が大きく、最適な判断をするために認知的負荷がかかります。この負荷がストレスを増幅させる主な要因となります。
不確実性による不安
プレイヤーは、展開を続けることで相手がどのような手札を得るかを予測できません。この「未来が見えない」状況が心理的な不安を引き起こし、意思決定の難しさをさらに強調します。
損失回避の心理
損失回避理論によれば、人は利益を得るよりも損失を避けることを優先する傾向があります。「増殖するG」を発動された場合、プレイヤーは「展開を止める」という選択で損失を最小限に抑えようとするため、この選択を強いられる状況そのものが心理的負荷を増加させます。
これらの要因が相互に作用し、「増殖するG」がプレイヤーに特有の心理的圧力を与えるカードとして機能していることが理論的に説明できます。
実験結果から導かれる結論: 「アンケート結果で見えた具体的な傾向」
本研究のアンケート調査結果から、「増殖するG」がプレイヤーに与える心理的影響の具体的な傾向が明らかになりました。
高いストレスと不安の存在
約64.5%の回答者が、「増殖するG」によって強い不安(スコア4以上)を感じていることが確認されました。特に「相手にアドバンテージを与える」不安が際立っており、52.9%が最高レベル(スコア5)を選択しました。
選択の自由がもたらすジレンマ
アンケート回答者の中で、「選択の自由があるが、その選択が不利な結果を引き起こす」という状況に対し、約76.9%が「リスク回避」の意識を強く持っている(4または5と回答)ことが示されました。
物理的制約との比較
他の手札誘発カード(灰流うららや無限泡影など)は、プレイヤーの行動を直接制約するため、ストレスが一貫して高いことがわかりました。一方で、「増殖するG」によるストレスはデッキやプレイヤーの選択によってばらつきが大きい特徴がありました(因子分析より)。
これらの結果から、「増殖するG」は物理的な妨害とは異なる「心理的妨害」として機能し、プレイヤーに独特な影響を与えていることが実証されました。
この結論に基づき、さらなる研究では、プレイヤーの経験や性格が心理的影響にどのように作用するかを検討し、「増殖するG」がゲーム全体の戦略やプレイスタイルに及ぼす影響をより詳細に分析することが期待されます。
今後の課題
本研究において、「増殖するG」がプレイヤーに与える心理的負荷について一定の知見が得られましたが、以下の点についてさらなる検討が必要であることが明らかになりました。
「増殖するGが通ることで展開を止めざるを得ないストレス」の再調査
本研究の本来のスコープである「増殖するGが通ることで展開を止めざるを得ないストレス」については、設問ミスから十分な考察ができませんでした。このストレスは、選択の自由が残された状況特有の心理的負荷として非常に重要な要素です。今後の研究では、特にこの点を中心にした再調査を行い、データの質と量を向上させることで、より詳細な分析を目指すべきです。
ストレスの質的な違いのさらなる考察
本研究では、「選択によるストレス」をはじめとした複数の異なるストレスの種類が存在することが明らかになりました。しかし、これらのストレスがプレイヤーの行動や心理にどのような具体的影響を及ぼしているかについては、まだ十分に明らかにされていません。今後は、ストレスの種類をさらに精査し、それぞれの心理的特性を解明することで、カードゲームにおけるストレスの多様性を理解するための基盤を構築していく必要があります。
研究結果の実践的応用
本研究の結果は、遊戯王OCGのゲームデザインにおける心理的負荷の調整や、プレイヤーのストレスマネジメントに活用できる可能性があります。特に、ストレスの種類やデッキタイプごとの差異を考慮したデザインにより、ゲーム体験をよりポジティブなものとすることが期待されます。これを踏まえ、研究成果を実務に反映させるための提言も今後の課題の一つです。
これらの課題を踏まえ、今後の研究ではアンケート設計やデータ分析手法の精緻化を図り、より深い洞察を得ることを目指します。これにより、「増殖するG」がもたらす心理的影響の全体像を解明し、遊戯王OCGのみならず他のカードゲームの設計にも寄与する研究成果を得ることができるでしょう。
おわりに
本稿では、「増殖するG」というカードがもたらす心理的圧力について、手札誘発カード全般と比較しながら考察を行いました。その結果、「増殖するG」は、選択を強いるストレスや不確実性による不安、損失回避の心理的傾向といった独自の心理的影響を与えることが明らかになりました。これらの影響は、他の手札誘発カードとは質的に異なるものであり、カードゲームにおける意思決定プロセスの複雑さを一層際立たせる要因となっています。
一方で、本研究にはまだ課題が多く残されています。「展開を止めざるを得ないストレス」についての詳細な分析、さらにはストレスの種類に関するさらなる考察など、次なるステップとして取り組むべきテーマが明確になりました。これらの課題を解決することで、より多面的で実践的な知見を得られると考えています。
なお、私は心理学や統計が専門ではないため、本稿には間違いや解釈の偏りが含まれている可能性があります。その際にはぜひご指摘いただけますと幸いです。皆様からのご意見をもとに、さらに良い内容に改善していきたいと考えております。
最後までお読みいただき、誠にありがとうございました。本考察が、遊戯王OCGやその他のカードゲームにおける心理的影響について理解を深める一助となれば幸いです。今後ともよろしくお願いいたします。
それではこの辺で.Good luck.
謝辞
まず、本レポートの原案をいただきましたぴにき様、ありがとうございました。
先述の通り元々の話題とは少々ズレてしまいましたが、綿密な調査が出来て良かったと思います。
加えて、本記事は本公開前に、複数名よりレビューを頂きました。
この場を借りて、厚く御礼申し上げます。
ありがとうございました。
特にalknightくんには詳細な技術的なレビューをいただきました、本当にありがとうございます。
ぴにき様
コメジルシ君
SSM君
alknight君
2war君
また,アンケートにご協力いただきました皆様にも改めて厚く御礼申し上げます.
本当にありがとうございました.
さらに追加で,本アンケートで使用している一部の図はMDCardCropperを用いて作成しました.
その開発者のpotato4d様に感謝申し上げます.素敵なツールをありがとうございました.
付録:使用したPythonスクリプト
今回の分析はテキストマイニング以外すべてPythonベースで実施しました.
参考程度に,使用したPythonのスクリプトを掲載しておきます.
デッキ分布の円グラフの描画
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib
# CSVファイルを読み込み
df = pd.read_csv('only-deck.csv')
# デッキごとの分布をカウント
deck_counts = df['deck'].value_counts()
# 分布数が1のものを除外
filtered_deck_counts = deck_counts[deck_counts > 1]
# 円グラフを描画
plt.figure(figsize=(10, 10))
plt.pie(filtered_deck_counts,
labels=filtered_deck_counts.index,
autopct='%1.1f%%',
startangle=90,
colors=plt.cm.Paired.colors)
plt.title('デッキ分布(分布数1を除外)')
plt.axis('equal') # 円を正円にする
plt.savefig('deck-circle.png')
plt.show()
分布数1のデッキのみをcsvにエクスポート
import pandas as pd
# CSVファイルを読み込み
df = pd.read_csv('only-deck.csv')
# デッキごとの分布をカウント
deck_counts = df['deck'].value_counts()
# 分布数が1のデッキを抽出
single_deck_counts = deck_counts[deck_counts == 1]
# 抽出結果をデータフレームに変換
single_deck_df = single_deck_counts.reset_index()
single_deck_df.columns = ['deck', 'count'] # 列名を指定
# CSVファイルとしてエクスポート
single_deck_df.to_csv('single_decks.csv', index=False, encoding='utf-8-sig')
print("分布数が1のデッキを 'single_decks.csv' にエクスポートしました。")基礎統計量の計算
import pandas as pd
import numpy as np
from datetime import datetime
datetime.now().strftime("%Y%m%d%H%M%S")
# データを読み込む
data = pd.read_csv('./data104kai.csv')
# カラムのリスト
likert_columns = ['Gストレス総合', 'G不安総合', 'G不安アド',
'G不安貧弱盤面', 'Gリスク', 'その他ストレス', 'その他不安']
data_numeric = data[likert_columns]
#print(data_numeric)
# 基礎統計量を計算
mean_values = data_numeric.mean()
median_values = data_numeric.median()
mode_values = data_numeric.mode().iloc[0] # 最頻値
variance_values = data_numeric.var()
std_dev_values = data_numeric.std()
# 有効数字4桁に丸めるために numpy の "round" を使う方法
def round_to_4sf(x):
if x == 0:
return 0 # 0はそのまま返す
else:
return round(x, 4 - int(np.floor(np.log10(abs(x))))) # 有効数字4桁に丸める
# 基礎統計量を有効数字4桁に丸める
mean_values = mean_values.apply(round_to_4sf)
median_values = median_values.apply(round_to_4sf)
mode_values = mode_values.apply(round_to_4sf)
variance_values = variance_values.apply(round_to_4sf)
std_dev_values = std_dev_values.apply(round_to_4sf)
# 結果をまとめたデータフレームを作成
basic_statistics = pd.DataFrame({
"平均値": mean_values,
"中央値": median_values,
"最頻値": mode_values,
"分散": variance_values,
"標準偏差": std_dev_values
})
# 結果を表示
print(basic_statistics)
timestampstr = return_time
# 結果をタイムスタンプ込みのCSVファイルに保存
basic_statistics.to_csv(datetime.now().strftime("%Y%m%d%H%M%S")+'basic_stats.csv')
相関係数とp値の計算
import seaborn as sns
import matplotlib.pyplot as plt
import pandas as pd
from datetime import datetime
import japanize_matplotlib
import scipy.stats as stats
import numpy as np
from datetime import datetime
def return_time(void):
timestamp_str = datetime.now().strftime("%Y%m%d%H%M%S")
return timestamp_str
data = pd.read_csv('./data104kai.csv')
# カラムのリスト
likert_columns = ['Gストレス総合', 'G不安総合', 'G不安アド',
'G不安貧弱盤面', 'Gリスク', 'その他ストレス', 'その他不安']
data_numeric = data[likert_columns]
# 相関係数を計算
correlation_matrix = data_numeric.corr()
# 現在の時刻を取得
timestamp_str = datetime.now().strftime("%Y%m%d%H%M%S")
# ヒートマップで相関係数の混同行列を表示
plt.figure(figsize=(10, 8))
sns.heatmap(correlation_matrix, annot=True, cmap="coolwarm", vmin=-1, vmax=1)
plt.title("Correlation Matrix for All Numeric Survey Items")
plt.savefig(timestamp_str+'corrheatmap.png')
plt.show()
# サンプルデータのロード(実データを読み込んでください)
# 不要な列を除外
data_numeric = data_numeric
# 相関係数とp値を計算する関数
def calculate_correlation_pvalues(df):
correlations = pd.DataFrame(index=df.columns, columns=df.columns)
p_values = pd.DataFrame(index=df.columns, columns=df.columns)
for col1 in df.columns:
for col2 in df.columns:
if col1 != col2:
corr, pval = stats.pearsonr(df[col1], df[col2])
correlations.loc[col1, col2] = corr
p_values.loc[col1, col2] = pval
else:
correlations.loc[col1, col2] = 1
p_values.loc[col1, col2] = np.nan
return correlations.astype(float), p_values.astype(float)
# 計算
correlation_matrix, p_value_matrix = calculate_correlation_pvalues(data_numeric)
# 現在の時刻を取得
timestamp_str = datetime.now().strftime("%Y%m%d%H%M%S")
# 結果表示
print("Correlation Matrix:\n", correlation_matrix)
print("\nP-value Matrix:\n", p_value_matrix)
correlation_matrixpd = pd.DataFrame(correlation_matrix)
correlation_matrixpd.to_csv(timestamp_str+'corrmatrix.csv')
p_value_matrixpd = pd.DataFrame(p_value_matrix)
p_value_matrixpd.to_csv(timestamp_str+'pmatrix.csv')マン=ホイットニーのU検定
from datetime import datetime
import pandas as pd
import scipy.stats as stats
def return_time(void):
timestamp_str = datetime.now().strftime("%Y%m%d%H%M%S")
return timestamp_str
# カラムのリスト
likert_columns = ['Gストレス総合', 'G不安総合', 'G不安アド',
'G不安貧弱盤面', 'Gリスク', 'その他ストレス', 'その他不安']
# 結果保存用データフレーム
u_test_results = pd.DataFrame(columns=['Question', 'U_statistic', 'U_p_value'])
# データの読み込み
data = pd.read_csv("./data104kai.csv") # データファイルのパスを指定
# 各項目でのマン=ホイットニーのU検定の実行
for col in likert_columns:
# MDとOCGのグループに分けてデータを抽出
md_group = data[data['format'] == 'MD'][col]
ocg_group = data[data['format'] == 'OCG'][col]
# マン=ホイットニーのU検定
u_statistic, u_p_value = stats.mannwhitneyu(md_group, ocg_group, alternative='two-sided')
# 結果を四捨五入し、新しいデータフレームを作成
result_df = pd.DataFrame({
'Question': [col],
'U_statistic': [round(u_statistic, 4)],
'U_p_value': [round(u_p_value, 4)]
})
# 結果を追加 (concatを使用)
u_test_results = pd.concat([u_test_results, result_df], ignore_index=True)
# 結果の表示と保存
print("マン=ホイットニーのU検定結果:\n", u_test_results)
# 保存時にファイル名を適切に設定
u_test_results.to_csv(f'{return_time}_u_test_results.csv', index=False)
Wilcoxon符号付順位検定
import pandas as pd
import scipy.stats as stats
import itertools # 全ての組み合わせを生成するために使用
# カラムのリスト
likert_columns = ['Gストレス総合', 'G不安総合', 'G不安アド',
'G不安貧弱盤面', 'Gリスク', 'その他ストレス', 'その他不安']
# 結果保存用データフレーム
wilcoxon_results = pd.DataFrame(columns=['Question', 'Wilcoxon_statistic', 'Wilcoxon_p_value'])
# データの読み込み
data = pd.read_csv("./data104kai.csv") # データファイルのパスを指定
# 全てのカラムの組み合わせを生成
column_combinations = itertools.combinations(likert_columns, 2)
# 各ペアについてWilcoxon符号付順位検定の実行
for col1, col2 in column_combinations:
# 各カラムのデータを取り出してNAを除去
col1_data = data[col1].dropna()
col2_data = data[col2].dropna()
# 両方のカラムにデータがある場合にのみWilcoxon検定を実行
if len(col1_data) > 1 and len(col2_data) > 1: # 1つ以上のデータがないと検定は実行できません
wilcoxon_stat, wilcoxon_p_value = stats.wilcoxon(col1_data, col2_data)
# 結果を四捨五入してデータフレームに追加
wilcoxon_results = pd.concat([wilcoxon_results, pd.DataFrame({
'Question': [f'{col1} vs {col2}'],
'Wilcoxon_statistic': [round(wilcoxon_stat, 4)],
'Wilcoxon_p_value': [round(wilcoxon_p_value, 4)]
})], ignore_index=True)
# 結果の表示と保存
print("\nWilcoxon符号付順位検定の結果:\n", wilcoxon_results)
wilcoxon_results.to_csv(f'{return_time}_wilcoxon_results.csv', index=False)
因子分析の事前調査
import pandas as pd
import numpy as np
from factor_analyzer import FactorAnalyzer
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
import seaborn as sns
# データフレームを仮定(実際のデータを読み込む)
df = pd.read_csv("data104kai.csv")
# カラムのリスト
likert_columns = ['Gストレス総合', 'G不安総合', 'G不安アド',
'G不安貧弱盤面', 'Gリスク', 'その他ストレス', 'その他不安']
# 選択されたリッカート尺度のカラムだけを選択
df_selected = df[likert_columns]
# 標準化
scaler = StandardScaler()
df_scaled = pd.DataFrame(scaler.fit_transform(df_selected), columns=likert_columns)
df_scaled
from factor_analyzer import calculate_kmo, calculate_bartlett_sphericity
# KMOテスト
kmo_all, kmo_model = calculate_kmo(df_scaled)
print(f"KMO Test: {kmo_model}")
# バートレットの球面性テスト
chi_square_value, p_value = calculate_bartlett_sphericity(df_scaled)
print(f"Bartlett's Test: chi-square = {chi_square_value}, p-value = {p_value}")
import japanize_matplotlib
# 固有値を計算
fa = FactorAnalyzer(rotation=None)
fa.fit(df_scaled)
# 固有値(eigenvalues)の取得
eigenvalues, _ = fa.get_eigenvalues()
# 固有値のプロット
plt.figure(figsize=(8, 6))
plt.plot(range(1, len(eigenvalues) + 1), eigenvalues, marker='o', linestyle='--')
plt.xlabel('因子の数')
plt.ylabel('固有値')
plt.title('因子数の決定(固有値プロット)')
plt.savefig('eigenvalues.png')
plt.show()
因子分析本体(importは省略)
# 因子数を3に設定して因子分析を実行
fa = FactorAnalyzer(n_factors=3, rotation='varimax')
fa.fit(df_scaled)
# 因子負荷量(Factor Loadings)の表示
loadings = fa.loadings_
pd.DataFrame(loadings).to_csv('loadings.csv')
print("因子負荷量:\n", loadings)
# 因子得点を取得
factor_scores = fa.transform(df_scaled)
df_factor_scores = pd.DataFrame(factor_scores, columns=[f'因子{i+1}' for i in range(factor_scores.shape[1])])
# 因子得点の表示
print(df_factor_scores)
df_factor_scores.to_csv('inshi.csv')3Dマップの描画
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D # 3Dプロット用
# 因子分析の実行
fa = FactorAnalyzer(n_factors=3, rotation='varimax')
fa.fit(df_scaled)
# 因子得点を取得
factor_scores = fa.transform(df_scaled)
df_factor_scores = pd.DataFrame(factor_scores, columns=[f'因子{i+1}' for i in range(factor_scores.shape[1])])
# deckカラムを取得
deck_values = df['deck']
# 3Dプロットの準備
fig = plt.figure(figsize=(50,50))
ax = fig.add_subplot(111, projection='3d')
# 因子得点(Factor Scores)を3D散布図としてプロット
sc = ax.scatter(df_factor_scores['因子1'], df_factor_scores['因子2'], df_factor_scores['因子3'], c='b', marker='o')
# 軸ラベルの設定
ax.set_xlabel('因子1')
ax.set_ylabel('因子2')
ax.set_zlabel('因子3')
# タイトルの設定
ax.set_title('因子得点の3D散布図')
# 各点にhogeの値を併記
for i in range(len(df_factor_scores)):
ax.text(df_factor_scores['因子1'][i], df_factor_scores['因子2'][i], df_factor_scores['因子3'][i], str(deck_values[i]), size=8, color='black')
# プロットの表示
plt.savefig('3dinshiwithdeck.png')
plt.show()1次元散布図の描画
import matplotlib.pyplot as plt
# データの準備
# df_factor_scoresが因子スコアを持つデータフレーム
# df_deckがデッキ名を含むデータフレームとします
df_factor_scores['deck'] = deck_values # デッキ名を結合
# 散布図プロット
plt.figure(figsize=(15, 100))
y = df_factor_scores['因子3'] # 因子1のスコア
x = [1] * len(y) # x軸は固定値
labels = df_factor_scores['deck'] # ラベルにデッキ名を使用
plt.scatter(x, y, alpha=0.7, color='blue') # 散布図を描画
# ラベルをデータポイントの横に追加
for i, label in enumerate(labels):
plt.text(x[i] + 0.05, y[i], label, fontsize=9, ha='left')
# 軸とタイトル
plt.ylabel('因子3スコア') # 因子1スコアをy軸に
plt.xticks([]) # x軸ラベルを非表示
plt.title('因子3スコアとデッキ名の対応散布図')
# グリッドの追加(任意)
plt.grid(axis='y', linestyle='--', alpha=0.7)
# 表示
plt.savefig('inshi3.png')
plt.tight_layout()
plt.show()
補足:統計的仮説検定の詳細
カイ二乗検定を実施しなかった理由
今回の分析では、回答データが順序尺度(5段階リッカート尺度)であったため、非カテゴリデータに適用可能なマン=ホイットニーのU検定やWilcoxon符号付き順位検定を採用しました。カイ二乗検定はカテゴリデータの分析により適しているため、本研究では適用していません。
t検定を実施しなかった理由
先ほどの説明と重複しますが、本研究ではストレスや不安の評価に5段階リッカート尺度の順序尺度を用いており、t検定のような平均値を前提とした分析手法ではデータの特性に適合しない可能性がありました。また、データの分布が正規分布に近いとは限らないため、より柔軟に適用できるノンパラメトリック検定(マンホイットニーのU検定やWilcoxon符号付き順位検定)を採用しました。さらに、複数の群を比較する必要がある場合にも、t検定より分散分析や別の手法の方が適切であると判断しました。
何故総当たりで相関分析と検定を実施したのか
本研究では、増殖するGが他の手札誘発カードと比較して特異な心理的影響を与えるかを明らかにすることを目的としていました。しかし、この領域においては事前の知見や仮説が限られており、初期段階として広範なデータを探索的に分析するアプローチを採用しました。具体的には、関連する心理的項目間の相関関係や順位の差を総当たりで検討することで、増殖するGが引き起こすストレス要素の構造的理解を目指しました。
補足:多重検定問題について
多重検定問題とは?
多重検定問題は、たくさんの検定(テストみたいなもの)を繰り返し行うと、「本当は違いがないのに、偶然『違いがある』と出てしまう」可能性が高くなる問題のことです。
例えば、サイコロを振って「1が出たらすごい!」というルールで遊ぶとします。サイコロを1回振ると、1が出る確率は6分の1(約16.7%)です。でも、6回振れば1回くらい1が出ることがあります。たくさん振るほど「偶然1が出る」可能性が増えていきます。
同じように、統計的な検定も、1回だけなら問題なくても、何回も行うと「偶然の結果」が増えてしまうのです。
なぜfalse positive(間違った結果)が増えるのか?
false positiveとは、「本当は違いがないのに、違いがあると判断してしまうこと」です。
100人に「何の関係もない質問」をして、結果を調べたとします。統計的なルールでは、5%の確率で「たまたま面白い結果(違いがあるように見える)」が出ることがあります。つまり、100回調べると5回くらいは「間違った結論」が出てしまうのです。
よって、たくさん検定を繰り返すほど、false positiveが増えるリスクがあります。
どうやって多重検定問題を防ぐのか?
false positiveを減らすために、いくつかの工夫があります。ここでは2つの方法を紹介します:
Bonferroni補正
検定の回数が増えるほど、間違いが増えるので、その分だけルールを厳しくする方法です。
「当たり」と判断する基準(p値)を小さくします。例えば、検定を10回やる場合、もとの基準(0.05)を10で割って「0.005」にします。これで間違いを減らせますが、少し厳しすぎることもあります。
FDR補正
Bonferroni補正より少し柔らかい方法です。「本当に重要な違いだけに注目する」ように調整します。これにより、false positiveを減らしながら、本当に意味のある結果を見逃さないようにします。
何故今回この問題に対処しなかったのか?
今回の研究では、多重検定問題への対策(Bonferroni補正やFDR補正)は行いませんでしたが、それには理由があります。
探索が目的だから
今回の研究は「増殖するGがどんな影響を与えているのか」を広く探るのが目的です。つまり、「何か面白い関係があるかも?」というヒントを見つける段階なので、まずは多くの検定を行う必要がありました。
仮説を作るための調査だから
多重検定を補正すると、面白そうなヒントも消えてしまうことがあります。今回は、「後で詳しい調査をするためのアイデアを探す」段階だったので、false positiveのリスクは受け入れました。
注意深く結果を見ているから
「これが確実に正しい!」とは主張せず、「こんな結果が出ましたが、偶然の可能性もありますよ」と説明して、慎重に結果を解釈しています。
多重検定問題のまとめ
多重検定問題は、たくさん検定すると「たまたま間違った結論」が出ることがある問題です。Bonferroni補正やFDR補正で間違いを減らすことができますが、今回は「面白いヒント」を広く探るため、補正を使いませんでした。
今後の研究で、さらに詳しい調査をする際には、こういった補正を使って正確な分析を行う予定です。
