
1-8 ローレンツ曲線・ジニ係数の説明 〜 格差の可視化
今回の統計トピック
ローレンツ曲線のグラフを作成して、ジニ係数を計算します!
公式問題集の準備
「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください!
「知る」「実践する」の章で、のんびり統計をお楽しみください!
問題を解く
📘公式問題集のカテゴリ
1変数記述統計の分野
問8 ローレンツ曲線・ジニ係数の説明(世界5か国の五分位階級所得割合)
試験実施年月
統計検定2級 2018年6月 問3(回答番号8)
問題
公式問題集をご参照ください。
解き方
ローレンツ曲線とジニ係数の概要
■ローレンツ曲線
ローレンツ曲線は、所得や財産などの経済的な量の集中度、平等/不平等を表現する曲線&グラフです。
■作り方
所得に関するローレンツ曲線の場合の例です。
所得金額の低い順に世帯等を並べます。
世帯等の数を一定幅の階級に区分します。
つまり、各階級の世帯等の数は同じ数になります。各階級の所得金額合計の累積相対度数を計算します。
累積相対度数=ローレンツ曲線をプロットします。
次の図は、五分位階級のローレンツ曲線を示しています。
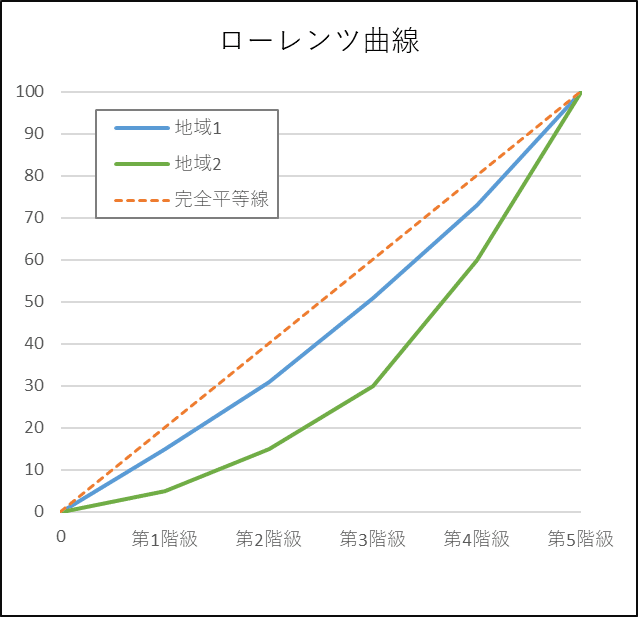
■完全平等線
五分位階級の場合、5階級のすべての相対度数が「20%」であれば「完全平等線」になります。
各階級の割合が同じ=格差が無い状態です。
累積相対度数が、第1階級20%、第2階級40%、第2階級60%、第4階級80%、第5階級100%となり、グラフは45度の直線になります。

■ローレンツ曲線と格差表現
図の地域1と地域2を比較すると、地域2の方が完全平等線を大きく下回っています。
ローレンツ曲線が完全平等線から下側に大きく乖離しているほど、格差が大きいと言われています。
地域2のヒストグラムを見てみましょう。

第1階級と第5階級の棒の高さは大きく異なっていて、格差が大きいことが分かります。
平等の場合の相対度数=20%と比べると、第1階級5%であり、かなり下回っています。一方で第5階級40%であり、かなり上回っています。
左側の階級が下方向に乖離して、右側の階級が上方向に乖離することによって、ローレンツ曲線は下方向に大きく曲がります。
左側の階級のほうが所得や財産の少ない層、右側の階級のほうが所得や財産の多い層ですので、ローレンツ曲線が下方向に大きく曲がる=不平等の度合いが高いことを表します。
これがローレンツ曲線の格差表現です。
■ジニ係数
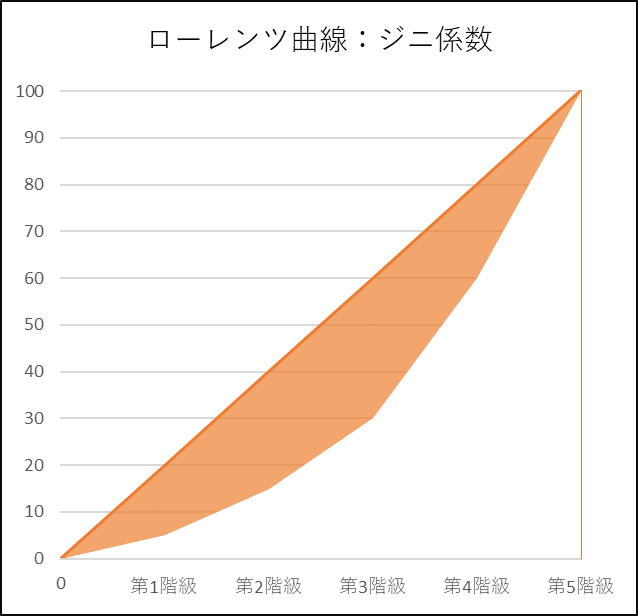
ジニ係数は完全平等線とローレンツ曲線(弧)の間の面積を2倍したものです。
次の図のオレンジの面積の2倍がジニ係数です。
ローレンツ曲線のグラフ全領域の面積は「1」です(横軸・縦軸とも1最大値が1)。
ジニ係数はこのグラフ全領域の面積に占める割合の値になります。
ジニ係数が0に近いほど平等、1に近いほど不平等を示します。
問題へ
問題に戻ります。
国名を変更しております。
5つの国のローレンツ曲線は完全平等線の下に弧を描くか?
問題では五分位階級を用いています。
すべての階級の相対度数が20%のときに完全平等線になります。
5つの国の各五分位階級の累積相対度数を完全平等線と比べてみましょう。
(四捨五入の丸め端数は第5五分位階級に含めました)

5つの国の累積相対度数は完全平等線を下回っています。
したがって、5つの国のローレンツ曲線は完全平等線の下に弧を描きます。
問題文Ⅰは正しいです。
J国・A国・D国のうち、ジニ係数が最も大きい国は?
まず、問題文の「ジニ係数が最も小さい国が最も不平等である」自体が誤りです。
ジニ係数は大きいほど不平等を表します。
3つの国のうち、ジニ係数が最も大きい国を考えましょう。
完全平等線の下方向に乖離するとジニ係数は大きくなります。
次の表は、完全平等線と4つの国の累積相対度数の「下方向の差」を表します。

A国の完全平等線との差は、すべての五分位階級でJ国・D国よりも大きいです。
つまり、A国のローレンツ曲線は、他の2つの国と比べて下側にプロットされます。
したがって、3つの国のうち、A国のジニ係数が最も大きいです。
問題文Ⅱは誤りです。
S国とC国のローレンツ曲線を比べると、C国のほうが完全平等線から乖離しているか?
完全平等線から下に向かって遠いほど不平等と言えます。
では、2つの国のローレンツ曲線のいずれが完全平等線から乖離しているかを考えましょう。
前の設問と同様に、完全平等線との下方向の差を見てみましょう。

C国の完全平等線との差は、すべての五分位階級でS国よりも大きいです。
つまり、C国のローレンツ曲線のほうが下側にプロットされます。
したがって、2つの国のうち、C国のローレンツ曲線のほうが完全平等線から離れており、不平等を示すことが分かります。
問題文Ⅲは正しいです。
解答
⑤です。
難易度 やさしい
・知識:ローレンツ曲線、ジニ係数
・計算力:電卓(低)
・時間目安:1~2分
知る
おしながき
公式問題集の問題に接近してみましょう!
ここでは、「労働政策研究・研修機構」公表の2022年版データブックの「第5-15表 五分位階級所得」を参照データとして利用します。
日本は厚生労働省の「2017年所得再分配調査」の2017年の値です。
その他の国は:The World Bank (2021年9月現在)による調査に基づき、アメリカ・ベルギー2018年、ドイツ・中国2016年、ブラジル2019年の値です。
【出典記載】
出典:労働政策研究・研修機構「データブック国際労働比較2022」207頁
【コンテンツ編集・加工の記載】
記事の記載にあたっては、労働政策研究・研修機構「データブック国際労働比較2022」を加工して作成しています。
今回はローレンツ曲線・ジニ係数に取り組みます。
ローレンツ曲線
📕公式テキスト:1.2.2 そのほかの図表の作成 4) ローレンツ曲線(13ページ~)
ローレンツ曲線とジニ係数の概要
「問題を解く」章の「ローレンツ曲線とジニ係数の概要」をお読みください。
5カ国の五分位階級所得割合
参照データより、日本、アメリカ、ベルギー、中国、ブラジルの値を用います。
資料上のジニ係数が最も小さな値がベルギー、最も大きな値がブラジルです。
五分位階級所得割合の相対度数/累積相対度数とジニ係数を表にしました。

■表の説明
「五分位階級所得割合」は「各家計の所得を少ない順から並べて人口で5等分したときの、それぞれの階級の所得の和の全体の所得に対する割合」です(出典資料より)。
累積相対度数は、相対度数を小さい階級から累積加算して計算します。
行「完全平等線」には、全五分位階級に均等に20%を設定しています。
列「0」は作図用のダミー数値です。
ローレンツ曲線の描画
横軸に五分位階級、縦軸に累積相対度数と完全平等線をプロットして、ローレンツ曲線を描きます。

ローレンツ曲線を読む
ジニ係数の最も小さいベルギーのローレンツ曲線が、完全平等線から最も近い線になります。
ジニ係数の最も大きいブラジルのローレンツ曲線が、完全平等線から最も遠い線になります。
日本、アメリカ、中国のローレンツ曲線は近いところにあります。
ジニ係数の差が0.1である日本とベルギー。
ローレンツ曲線で可視化すると、ジニ係数の違いがこのような間隔を生み出すんですね、
ジニ係数を計算する
完全平等線とローレンツ曲線の間(図のオレンジの領域)は、5つの階級ごとに「台形」(両端は三角形)に分割できます。
5つの台形(または三角形)の面積を計算して、5階級分を合算し、最後に2倍するとジニ係数になります。
・上底・下底は、完全平等線と各国の相対度数の差です。
・高さは階級の幅です。五分位階級の場合は、0.2です。


【注意】
ここで計算したジニ係数と参照データのジニ係数の値は相違します。
相違理由は不明です。
参照データのジニ係数の計算に用いたデータや方法が相違する可能性があります。
【別の計算方法】
完全平等線よりも下の面積は、0.5です。
ローレンツ曲線よりも下の面積(図の白い領域の面積)を求めます。
1の0.5から2の計算結果を引きます。
完全平等線とローレンツ曲線の間の面積が求まります。3の値を2倍するとジニ係数です。
または、3の値を1の値で割ってもジニ係数を求められます。
実践する
ローレンツ曲線を書いてジニ係数を計算してみよう
「五分位階級所得」を掲載する「データブック国際労働比較2022」は「労働政策研究・研修機構」のホームページで公開されています。
「データブック国際労働比較」のページで「データブック国際労働比較2022」のpdfファイルをダウンロードできます。
「第5-15表 五分位階級所得割合」は207ページに掲載されています。
CSVファイルのダウンロード
こちらのリンクから整形後のCSVファイルをダウンロードできます。
Pythonサンプルファイルを利用する方は、このCSVファイルをダウンロードしてください。
出典資料「第5-15表 五分位階級所得割合」の項目を次の順に並べ替えて、単位を%(0~100)から比率(0~1)に変更しました。
【項目順】
国名,略名,年度,第1十分位,第1五分位,第2五分位,第3五分位,第4五分位,第5五分位,第10十分位,ジニ係数,出典
電卓・手作業で作成してみよう!
上述の方法でデータを取得して、または、「知る」の相対度数を利用して、電卓やそろばんをはじいて累積相対度数を計算し、手作業でローレンツ曲線を描き、ジニ係数を計算してみましょう!
一番記憶に残る方法ですし、試験本番の電卓作業のトレーニングにもなります。
きれいな色のペン・色鉛筆でカラフルなグラフを描くと、作業が楽しくなりそうです。
EXCELで作成してみよう!
データ数が多い場合、やはり手作業では非効率になります。
パソコンを利用して、手早く作表できるようになれば、実務活用がしやすくなるでしょう。
ローレンツ曲線のグラフ
ローレンツ曲線専用の機能は見当たりませんでした。
ここでは、相対度数データから累積相対度数を算出の上、5カ国のデータを一度に範囲指定して折れ線グラフを作成します。

■グラフの選択
①累積相対度数の表を列名を含めて範囲指定します。
②メニューの挿入を選択します。
③リボンの「グラフ」の右隅の矢印ボタンを選択します。
④「グラフの挿入」画面が開きます。「すべてのグラフ」タブで折れ線グラフを選択します。
⑤折れ線を選択します。

■グラフの軸の変更
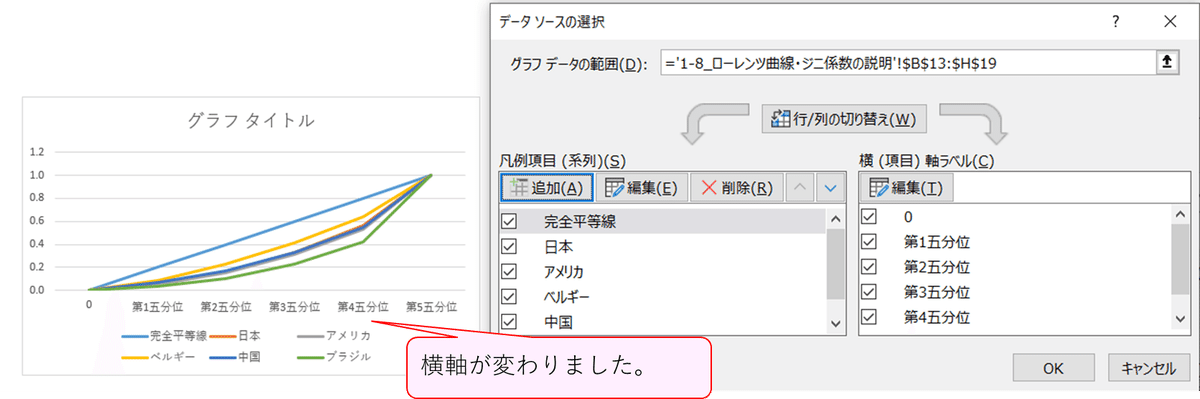
次の図のように横軸が国になってしまった場合の補正方法です。

グラフを右クリックして、メニューの「データの選択」を指定します。

データソースの選択画面で、「行/列の切り替え」ボタンを押します。
これでOKです。

行/列の切り替えを行うと、グラフの横軸が五分位に変わります。
ジニ係数の計算
累積相対度数の表から、台形の面積:(上底+下底)× 高さ ÷2の計算式を設定して、ジニ係数を求めます。
台形の面積の計算に利用する情報は次のように得られます。
・上底:1つ前の五分位の「完全平等線と国の値の差」
・下底:対象の五分位の「完全平等線と国の値の差」
・高さ:完全平等線の対象の五分位と1つ前の五分位の差(0.2です)

EXCELサンプルファイルのダウンロード
こちらのリンクからEXCELサンプルファイルをダウンロードできます。
Pythonで作成してみよう!
プログラムコードを読んで、データを流したりデータを変えてみたりして、データを追いかけることで、作表ロジックを把握する方法も効果的でしょう。
サンプルコードを揃えておけば、類似する作表作業を自動化して素早く結果を得ることができます。
今回は5か国のローレンツ曲線の描画、ジニ係数の計算と25か国比較グラフに取り組んでみましょう。
①ライブラリのインポート
主にpandasとmatplotlibを使用します。
import pandas as pd
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'MS Gothic'
%matplotlib inline②CSVファイルの読み込み
まず、上述のダウンロードリンクより、CSVファイルをダウンロードします。
その後、次のコードを実行して、CSVファイルをpandasのデータフレームに読み込みます。
datafile = './sample_data.csv' # CSVファイルの格納フォルダとファイル名を設定
df = pd.read_csv(datafile)
print(df.shape)
display(df.head())
③累積相対度数の計算
pandasのcumsumを利用して、第1五分位から第5五分位までの累積相対度数を計算して、df_cumsumを作成します。
# 累積相対度数を計算してdf_cumsumに設定
df_cumsum = pd.DataFrame(df.iloc[:, 4:9].cumsum(axis=1))
# df_cumsum.columns = [f'{df.columns[i]}_累積' for i in range(4,9)]
# df_cumsum の列に国名と0を追加、第5五分位を1で置き換え
df_cumsum = pd.concat([df[['国名']], df_cumsum], axis=1)
df_cumsum.insert(1, '0', 0)
df_cumsum['第5五分位'] = 1.0
# 日本の2レコードの削除&index再作成
df_cumsum.drop(index=[1, 2], inplace=True)
df_cumsum = df_cumsum.reset_index(drop=True)
print(df_cumsum.shape)
display(df_cumsum.head())
④ローレンツ曲線の表示
pandasのplotで折れ線グラフをプロットします。
countries_dict(辞書型)に表示対象国と各国の線の色を設定します。
# 表示対象国のリスト(国ごとに線の色を設定)
countries_dict = {'ベルギー': 'orangered',
'日本': 'darkgreen',
'中国': 'red',
'アメリカ': 'navy',
'ブラジル': 'blue',
}
plt.figure(figsize=(6,6))
# 完全平等線のプロット
x = [0, 1, 2, 3, 4, 5]
y = [0.0, 0.2, 0.4, 0.6, 0.8, 1.0]
plt.plot(x, y, lw=0.5, ls='--', c='tomato', label='完全平等線')
# ローレンツ曲線のプロット
for country, color in countries_dict.items():
idx = df_cumsum[(df_cumsum['国名']==country)].index
df_cumsum.iloc[idx[0], 1:len(x)+1].plot(rot=0, lw=0.5, label=country, c=color)
# グラフの修飾
plt.grid(linestyle=':', c='gray', linewidth=0.5)
plt.title('ローレンツ曲線')
plt.xlabel('家計数の累積相対度数(各階級=0.2)')
plt.ylabel('所得の累積相対度数')
plt.legend()
plt.tight_layout()
# plt.savefig('./lorenz_curve.png') # グラフ画像ファイルの保存
plt.show()
⑤ジニ係数の計算
データフレームdf_cumsum(25か国のデータ)の列にジニ係数を追加します。
jini_half(リスト)には、完全平等線と各国のローレンツ曲線との間の「台形(or三角形)」の面積を設定しています。
jini_half = [0] * len(df_cumsum)
for i in range(1, 6):
jini_half += ((y[i-1] - df_cumsum.iloc[:, i]) + (y[i] - df_cumsum.iloc[:, i+1])) \
* (y[i] - y[i-1]) / 2
df_cumsum = pd.concat([df_cumsum, pd.Series(jini_half*2, name='ジニ係数')], axis=1)
print(df_cumsum.shape)
display(df_cumsum.head())
⑥ジニ係数のグラフ表示
pandasのplot.barで各国のジニ係数の棒グラフをプロットします。
ジニ係数の昇順に並び替えしています。
# ジニ係数で昇順ソート
df_sorted = df_cumsum.sort_values('ジニ係数', ascending=True)
# ジニ係数の平均、y軸の最小値・最大値を計算
jini_mean = df_sorted['ジニ係数'].mean()
y_lim_min = int(df_sorted['ジニ係数'].min() / 0.05) * 0.05 - 0.05
y_lim_max = int(df_sorted['ジニ係数'].max() / 0.05) * 0.05 + 0.05
# ジニ係数のプロット
df_sorted.plot.bar(x=df_sorted.columns[0], y=df_sorted.columns[7],
figsize=(10, 5), ylim=[y_lim_min, y_lim_max],
color='seagreen', rot=60, title='ジニ係数の比較')
# グラフの修飾
plt.grid(linestyle=':', c='gray', linewidth=0.5)
plt.axhline(y=jini_mean, xmin=0, xmax=1, lw=0.5, c='tomato')
plt.text(0.5, jini_mean+0.005, f'平均( {jini_mean:.3f} )', color='tomato')
plt.tight_layout()
# plt.savefig('./jini_coef.png') # グラフ画像ファイルの保存
plt.show()
25か国比較をしてみて、日本のジニ係数は高い方に寄っていることが分かりました。
Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。
おわりに
世の中にはいろんな統計情報が公開されているのですね。
この連載を始めてから、さまざまなサイトの統計情報を見る機会が激増しました。
政府系はExcel形式でデータ提供するケースが多い所感です。
ユニークな表現形式も見られます。
つぶやき:プログラムで加工しやすい形式でデータ提供していただけると嬉しい。。。
最後までお読みいただきまして、ありがとうございました。
のんびり統計シリーズの記事
次の記事
前の記事
目次
