
数学とPython 6 ベクトル ~可視化・numpy変換
はじめに
シリーズ数学とPythonのご案内
「シリーズ数学とPython」は、数学の学習中に「解けない、無理~」と焦ったときに、Pythonで数値の動きや可視化を行って、理解の糸口を見つけたときのことを記事にします。
データサイエンス数学ストラテジスト上級公式問題集
この記事は「データサイエンス数学ストラテジスト上級公式問題集」の問題の解読中に見つけたヒントを取り扱います。
今回取り組む問題
問題30「ベクトルの大きさの最小値は?」
Python実装
やりたいこと
解答で得られた3つのベクトルを平面にプロットします。
作戦
ベクトルの演算を SymPy で行ったつもりになります。
その後、numpy で扱える配列に変換して、matplotlib の quiver でベクトルを描画します。
実装の開始
インポート
### インポート
import sympy
import matplotlib.pyplot as plt
sympy.init_printing;ベクトルの定義
ベクトル$${\vec{a},\ \vec{b},\ \vec{p}}$$を sympy の Matrix で定義します。
問題集の問題を解く過程を「おまけ」に記載しました。
ここでは計算結果を定義します。
### ベクトルaの定義
vec_a = sympy.Matrix([[2], [-1]])
vec_a
### ベクトルbの定義
vec_b = sympy.Matrix([[-1], [3]])
vec_b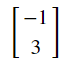
### ベクトルpの定義(解を得た後)
vec_p = sympy.Matrix([[1], [2]])
vec_p
sympyのベクトルをnumpyの配列に変換
sympy の matrix2numpy で sympy で定義したベクトルを numpy配列に変換します。
「おまけ」の解答過程で利用した sympy のベクトルを変換するテイでお送りいたします。
### sympyのベクトルをnumpy配列に変換(あわせてfloat型に変換)
vec_a_np = sympy.matrix2numpy(vec_a).astype(float)
vec_b_np = sympy.matrix2numpy(vec_b).astype(float)
vec_p_np = sympy.matrix2numpy(vec_p).astype(float)ベクトルの描画
matplotlib の quiver で3つのベクトルを描画します。
矢印 が付きます。始点は [0, 0] です。
### プロット
fig, ax = plt.subplots()
ax.set_aspect('equal')
# quiver(始点x(省略時0), 始点y(省略時0)、x成分, y成分)
ax.quiver(vec_a_np[0,0], vec_a_np[1,0], color='red', label='$\\vec{a}$',
angles='xy', scale_units='xy', scale=1)
ax.quiver(vec_b_np[0,0], vec_b_np[1,0], color='blue', label='$\\vec{b}$',
angles='xy', scale_units='xy', scale=1)
ax.quiver(vec_p_np[0,0], vec_p_np[1,0], color='green', label='$\\vec{p},\ k=1$',
angles='xy', scale_units='xy', scale=1)
# 修飾
ax.grid(lw=0.5, ls='--')
ax.axvline(0, lw=0.5, color='black')
ax.axhline(0, lw=0.5, color='black')
ax.set_xlim(-1.5, 3.5), ax.set_ylim(-1.5, 3.5)
ax.legend()
plt.show()
予想通りのグラフでしたか?
今回も可視化できてよかったです!
(数式と比べて優しい温もりを感じます😉)
おまけ
Pythonで問題集の問題を解くコードです。
Jupyter Notebook のセル(計算ステップ)ごとに、計算結果を表示しています。
グラフ描画まで繋がります。
### インポート
import sympy
import matplotlib.pyplot as plt
sympy.init_printing;### 変数の定義 正の実数
k = sympy.Symbol('k', positive=True)### ベクトルaの定義
vec_a = sympy.Matrix([[2], [-1]])
vec_a### ベクトルbの定義
vec_b = sympy.Matrix([[-1], [3]])
vec_b### ベクトルpの定義
vec_p = k * vec_a + vec_b
vec_p### ベクトルpの大きさ(ノルム)をnormメソッドで計算
# expand関数でノルム計算結果を展開する
norm_vec_p = sympy.expand(vec_p.norm())
norm_vec_p### 変数kの区間[-1, 3/2]でベクトルpの大きさの最小値mを計算
# 最小値:sympy.minimum( 関数, 変数k, Interval(変数の区間下端, 上端))
m = sympy.minimum(norm_vec_p, k, sympy.Interval(-1, 3/2))
m### m^2を計算 ★解答
m**2### ベクトルpの変数kに1を代入
vec_p_1 = vec_p.subs(k, 1)
vec_p_1### プロット
fig, ax = plt.subplots()
ax.set_aspect('equal')
# quiver(始点x(省略時0), 始点y(省略時0)、x成分, y成分)
ax.quiver(vec_a_np[0,0], vec_a_np[1,0], color='red', label='$\\vec{a}$',
angles='xy', scale_units='xy', scale=1)
ax.quiver(vec_b_np[0,0], vec_b_np[1,0], color='blue', label='$\\vec{b}$',
angles='xy', scale_units='xy', scale=1)
ax.quiver(vec_p_1_np[0,0], vec_p_1_np[1,0], color='green', label='$\\vec{p},\ k=1$',
angles='xy', scale_units='xy', scale=1)
# 修飾
ax.grid(lw=0.5, ls='--')
ax.axvline(0, lw=0.5, color='black')
ax.axhline(0, lw=0.5, color='black')
ax.set_xlim(-1.5, 3.5), ax.set_ylim(-1.5, 3.5)
ax.legend()
plt.show()おわりに
ベクトルの記号と成分表示と座標表示がいまひとつ繋がらず(特に座標表示)、グラフをプロットすることで、なんとか3者が結びつくといいな、って思っています。
おわり
ブログの紹介
noteで3つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
2.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
3.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
