
5-6 分布形と歪度・尖度 ~ 主要な確率分布の形状と歪度・尖度の可視化
今回の統計トピック
「期待値」「分散」「歪度」「尖度」に迫ります。
さまざまな確率分布の形状をグラフで可視化して、歪み/尖りの指標である歪度と尖度を確認します。
モーメントと「期待値」「分散」「歪度」「尖度」の関係も明らかになります!
公式問題集の準備
「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください!
「知る」「実践する」の章で、のんびり統計をお楽しみください!
問題を解く
📘公式問題集のカテゴリ
確率分布の分野
問6 分布形と歪度・尖度(データなし)
試験実施年月
統計検定2級 2018年11月 問11(回答番号19)
問題
公式問題集をご参照ください。
解き方
題意
歪度・尖度について、分布の形状(グラフの形状)の理解を確認する問題です。
歪度・尖度の指標は、正規分布の歪度=0、正規分布の尖度=0を基準にしています。
実際にグラフの形状を確認しましょう。
今回のグラフは、さまざまな確率密度関数の値をプロットして作成しています。
また歪度・尖度の計算にはデータを母集団として扱う場合の計算式を用いています。
歪度を可視化する
歪度(わいど)は左右の非対称性の度合いを測る指標です。
歪度の異なるグラフを見てみましょう。
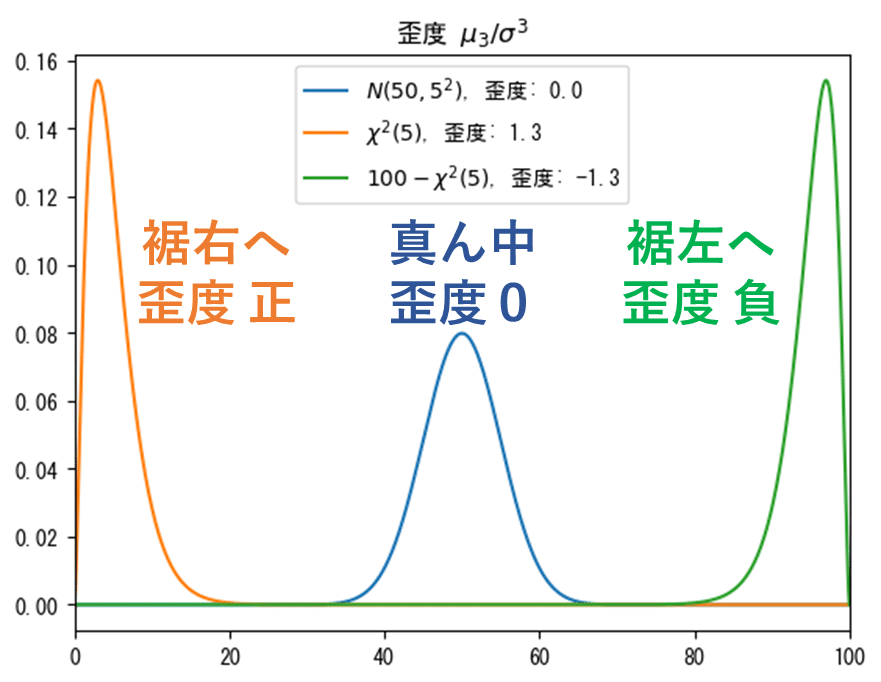
■裾が左右対称=歪度が0
ブルーは「真ん中に峰があって裾が左右対称」の分布です。
歪度は「ゼロ」です。
■右に裾が長い=歪度が正
オレンジは「左に峰が寄っていて右に裾が長い」分布です。
歪度は 1.3 で「正」です。
■左に裾が長い=歪度が負
グリーンは「右に峰が寄っていて左に裾が長い」分布です。
歪度は -1.3 で「負」です。
右に裾が長い分布は歪度が正の値、左に裾が長い分布は歪度が負の値です。
問題文1は誤りです。
尖度を可視化する
尖度(せんど)は平均付近の尖り具合と分布の裾の長さの度合いを測る指標です。
尖度の異なるグラフを見てみましょう。

■尖度が0
ブルーを基準にして他のプロットを見ましょう。
■中心部の尖りが大きく裾が長い=尖度が正
オレンジは「中心部の尖りが大きく裾が長い」分布です。
尖度は 2.4 で「正」です。
■中心部が平坦で裾が短い=尖度が負
グリーンは「中心部が平坦で裾が短い」分布です。
歪度は -1.2で「負」です。
中心部が平坦で裾が短い分布は尖度が負の値、中心部が尖って裾が長い分布は尖度が正の値です。
問題文2は誤りです。
$${\boldsymbol{t}}$$分布を可視化する
自由度 1、4、10、100 の$${t}$$分布のグラフです。

歪度はいずれもゼロです(自由度>3)。
尖度は、自由度が大きいほど絶対値が小さくなっています。
自由度$${v(v>3)}$$の$${t}$$分布の歪度は0になり、自由度$${v(v>4)}$$の$${t}$$分布の尖度は自由度が大きいほど絶対値が小さくなります。
問題文3は誤りです。
解答
⑤ すべて誤り です。
難易度 ふつう
・知識:歪度、尖度、$${t}$$分布
・計算力:なし
・時間目安:1分
知る
おしながき
公式問題集の問題に接近してみましょう!
今回は、さまざまな歪度・尖度を図表と数式で見える化してまいりましょう!
歪度・尖度
📕公式テキスト:2.6 モーメント(70ページ~)
歪度(わいど)と尖度(せんど)は、確率分布の特徴を示す指標であり、期待値$${E[X]=\mu}$$や分散$${V[X]=\sigma^2}$$の仲間(兄弟?)です。
期待値・分散・歪度・尖度の形状
まずは正規分布を例にして、期待値と分散を確認しましょう。
期待値は重心を示し、期待値の変動は横方向( x 軸方向)のズレになります。
図は期待値 $${-1}$$(グリーン)、$${0}$$(ブルー)、$${1}$$(オレンジ) の3種類をプロットしています。
分散はバラツキを示し、分散の変動は峰の高さ、裾の長さ・厚みに変化を与えます。
図は分散 $${1}$$(ブルー)、$${2^2}$$(オレンジ)、$${3^2}$$(グリーン) の3種類をプロットしています。

続いて歪度と尖度を確認しましょう。
歪度は左右非対称の度合いを示し、右に裾が長いと正の値(オレンジの線)、左に裾が長いと負の値(グリーンの線)になる性質を持ちます。
図は歪度 $${1.3}$$ (オレンジ)、$${0}$$(ブルー)、$${-1.3}$$(グリーン) の3種類をプロットしています。
裾がワイド(wide=幅)ですね!

尖度は峰の尖り具合と裾の長さに関連する指標であり、中心部が尖っていて裾が長いと正の値(オレンジの線)、中心部が平坦・裾が短いと負の値(グリーンの線)になる性質を持ちます。
図は歪度 $${2.4}$$ (オレンジ)、$${0}$$(ブルー)、$${-1.2}$$ (グリーン) の3種類をプロットしています。
鮮度が命です!(そんなことはない)
期待値・分散・歪度・尖度の数式
モーメントという概念を取り入れると、この人達は同じお母さんから生み出されることが分かります。
この先、数式が多くなります。
眠気注意です。
飛ばしていただいても大丈夫です。

1番ファースト、期待値です。
■期待値の公式
$${E[X] \equiv \begin{cases} \displaystyle \sum_i x_i f(x_i)=\mu &離散型の確率変数\\ \displaystyle \int^{\infty}_{-\infty} x f(x) dx=\mu &連続型の確率変数 \end{cases} }$$
$${E[X]}$$は$${E[X^1]=\mu}$$です。

2番セカンド、分散です。
■分散の公式
$${V[X] \equiv E[(X - \mu)^2]= \begin{cases} \displaystyle \sum_i (x_i - \mu)^2 f(x_i)=\sigma^2 &離散型の確率変数\\ \displaystyle \int^{\infty}_{-\infty} (x - \mu)^2 f(x) dx=\sigma^2 &連続型の確率変数 \end{cases} }$$
$${V[X]}$$は$${E[(X - \mu)^2]}$$であり2乗です。
かっこをほぐすと$${E[(X - \mu)^2]=E[X^2]-\mu^2}$$になります。

3番サード、歪度です。
■歪度の公式
$${E[(X-\mu)^3]/\sigma^3}$$
歪度には$${E[(X-\mu)^3]}$$が含まれており、3乗です。
かっこをほぐすと$${E[(X-\mu)^3]=E[X^3]-3 \mu E[X^2]+2 \mu^3}$$になります。

4番フォース、尖度です。
■尖度の公式
・$${E[(X-\mu)^4]/\sigma^4-3}$$:正規分布の尖度を0にする場合
・$${E[(X-\mu)^4]/\sigma^4}$$:正規分布の尖度を3にする場合
歪度には$${E[(X-\mu)^4]}$$が含まれており、4乗です。
かっこをほぐすと$${E[(X-\mu)^4]=E[X^4]-4\mu E[X^3]+6\mu^2 E[X^2]-3\mu^4}$$になります。

$${E[X^k]}$$と$${E[(X - \mu)^k]}$$に、たくさんの$${k}$$乗が現れました。
モーメント
$${k}$$乗を$${k}$$次にまとめます。

■$${k}$$次の原点のまわりのモーメント $${E[X^k]}$$
確率変数$${X^k}$$の期待値$${E[X^k]}$$を「$${k}$$次の原点のまわりのモーメント」と呼びます。
1次の原点のまわりのモーメント$${E[X]}$$は確率変数$${X}$$の期待値=平均$${\mu}$$です。
■$${k}$$次の平均のまわりのモーメント $${E[(X-\mu)^k]}$$
確率変数$${(X-\mu)^k}$$の期待値$${E[(X-\mu)^k]}$$を「$${k}$$次の平均のまわりのモーメント」と呼びます。
また、公式テキストでは$${k}$$次の平均のまわりのモーメントの表記に$${\mu_k}$$を用いて、$${\mu_k \equiv E[(X-\mu)^k]}$$と表しています。
平均$${\mu}$$を引いていて「平均のまわり」にしています。
2次の平均のまわりのモーメント$${E[(X-\mu)^2]}$$は確率変数$${X}$$の分散$${V[X]}$$です。
■$${k}$$次の標準化モーメント $${E[\{(X-\mu)/\sigma\}^k]}$$
確率変数$${\{(X-\mu)/\sigma\}^k}$$の期待値$${E[\{(X-\mu)/\sigma\}^k]}$$を「$${k}$$次の標準化モーメント」と呼びます。
3次の標準化モーメント$${E[\{(X-\mu)/\sigma\}^3]}$$は確率変数$${X}$$の歪度です。
4次の標準化モーメント$${E[\{(X-\mu)/\sigma\}^4]}$$は確率変数$${X}$$の尖度です。
モーメントのグラウンドに期待値、分散、歪度、尖度が勢ぞろいしました!

モーメント母関数
お母さんの登場です。
確率変数$${X}$$にかかる$${e^{tX}}$$と確率密度(質量)関数$${f(x)}$$からモーメント母関数$${M_X(t)=E[e^{tX}]}$$を求めます。

■モーメント母関数の公式
$${M_X(t) =E[e^{tX}]= \begin{cases} \displaystyle \sum_i e^{tx_i} f(x_i) &離散型の確率変数\\ \displaystyle \int^{\infty}_{-\infty} e^{tx} f(x) dx &連続型の確率変数 \end{cases} }$$
そしてそして、モーメント母関数を微分することによって、$${k}$$次の原点のまわりのモーメント $${E[X^k]}$$が生み出されます!
具体的には、モーメント母関数$${M_X(t)=E[e^{tX}]}$$を微分してから$${t=0}$$を代入します。
次のように微分を繰り返すことによって、モーメント母関数から「$${k}$$次の原点のまわりのモーメント$${E[X^k]}$$」を導出できるのです!
・$${0}$$階微分$${M_X(0)=E[1]=1}$$
・$${1}$$階微分$${M_X^{'}(0)=E[X]}$$($${1}$$次の原点のまわりのモーメント)
・$${2}$$階微分$${M_X^{''}(0)=E[X^2]}$$($${2}$$次の原点のまわりのモーメント)
・$${3}$$階微分$${M_X^{'''}(0)=E[X^3]}$$($${3}$$次の原点のまわりのモーメント)
・$${k}$$階微分$${M_X^{{k}}(0)=E[X^k]}$$($${k}$$次の原点のまわりのモーメント)
期待値、分散、歪度、尖度に現れる$${E[X^k]}$$をモーメント母関数が生み出すことが分かりました。
母なる関数に感謝です。

そして大事な天王山を最後まで観戦・応援してくださり、ありがとうございます!

【謝辞】
モーメントの記載にあたっては、次の書籍を参考にいたしました。
統計学入門書の名著です。
ありがとうございました!
この書籍には次のような記述があります。
モーメント母関数から、期待値、分散、歪度、尖度など、重要なモーメントが、やっかいな計算をすることなく、比較的簡単な微分の計算から求められる。モーメント母関数は、多くの役に立つ性質を持つが、これもその一つである。
心強いです!
また、参考書籍の読解にあたっては、次のサイトを参考にいたしました。
ありがとうございました!
マクローリン展開など、モーメント母関数導出の数学的な説明が充実しています。
エンディングの雰囲気を醸してみましたが、まだ1テーマ残っています!
$${t}$$分布を覗いてみましょう。
t分布
📕公式テキスト:2.10.2 $${t}$$分布(89ページ~)
$${t}$$分布は区間推定・統計的仮説検定で大活躍する確率分布です。
公式問題集や公式テキストの巻末には$${t}$$分布のパーセント点表(上側確率表)が掲載され、この表は今後度々出現することでしょう。
$${\boldsymbol{t}}$$分布の形状
$${t}$$分布のパラメータは「自由度」です。
自由度 1, 4, 10, 100 の$${t}$$分布をプロットしました。

左右対称の形状です。
自由度の値が大きくなるにつれて峰の尖りが大きくなります。
どんどん自由度を大きくすると、標準正規分布$${N(0,1)}$$の確率密度関数に近づきます。
$${\boldsymbol{t}}$$分布あれこれ
■確率変数$${t}$$
2つの独立な確率変数$${Z}$$と$${W}$$について、$${Z}$$が標準正規分布$${N(0,1)}$$に従い、$${W}$$が自由度$${m}$$の$${\chi^2}$$分布に従うとき、確率変数$${t=\cfrac{Z}{\sqrt{W/m}}}$$が従う分布を自由度$${m}$$の$${t}$$分布と呼び、$${t(m)}$$と表します。
■期待値
$${E[t]=0}$$、ただし自由度$${m>1}$$
■分散
$${V[t]= \begin{cases} \cfrac{m}{m-2} &自由度m>2 \\ \infty & 1 < 自由度 m\leq 2\end{cases}}$$
■歪度
歪度$${=0}$$、ただし自由度$${m>3}$$
■尖度
尖度$${=\cfrac{6}{m-4}}$$、ただし自由度$${m>4}$$
$${t}$$分布に近づいてみました。

実践する
歪度と尖度を体感してみよう!
さまざまなデータの歪度と尖度を計算したり、グラフを描いて形状を確認しましょう!
EXCELを活用して、さまざまなデータのグラフの形状、歪度、尖度をシミュレートしていきましょう!
Pythonコードでサクサク図表化しましょう。
電卓・手作業で作成してみよう!
「EXCELで作成してみよう!」の内容を参照しつつ、気になるデータについて度数分布表とヒストグラムを作成して、歪度・尖度を計算してみましょう。
一番記憶に残る方法ですし、試験本番の電卓作業のトレーニングにもなります。
EXCELで作成してみよう!
データ数が多い場合、やはり手作業では非効率になります。
パソコンを利用して、手早く作表できるようになれば、実務活用がしやすくなるでしょう。
データシートの紹介
100個のデータを持つ「データセット」を7つ作り、それぞれの度数分布表とヒストグラムを作成しました。
データシート(抜粋)は次のような雰囲気です。


【データセット】の数値を変えると、連動してヒストグラムの形状が変わり、歪度・尖度の数値も変わります。
ぜひ、データセットの数値を変えて、データの分布と歪度・尖度の関係を体感してください!
歪度・尖度の計算
EXCELの関数を用いて、データセットの各値に基づく歪度・尖度を算出します。
シートの歪度・尖度は小数第1位で丸めています。
■歪度 SKEW関数
=SKEW( データセットの範囲 )
■尖度 KURT関数
=KURT( データセットの範囲 )
ちなみに情報 ~データは母集団?標本?~
EXCELの歪度と尖度の関数には次のような特徴があります。
・歪度の関数は「SKEW.P関数」と「SKEW関数」の2種類あります。
・尖度の関数は「KURT関数」の1種類です。
2つの違いをざっくりと。
・「.P」がつく関数は与えられたデータを「母集団データ」として扱って計算します。
・「.P」がつかない関数は与えられたデータを「標本データ」として扱い、標本データから母集団の統計量を推定計算します。
今回のデータシートでは、基準を統一する観点から、データを標本データとして扱う「SKEW関数」と「KURT関数」を利用しました。
なお、「問題を解く」「知る」「Pythonで作成してみよう!」では、公式テキスト§2.6に沿って、母集団データとして扱う計算をしています。
EXCELの歪度・尖度と異なりますので、ご注意くださいませ。
計算式の相違内容です。
■歪度「SKEW.P関数」(公式テキスト§2.6の計算式と同じ)
$${\cfrac{E[(X-\mu)^3]}{\sigma^3}=\cfrac{1}{n} \displaystyle \sum ^n_{i=1} \left( \cfrac{x_i-\mu}{\sigma} \right)^3}$$
■歪度「SKEW関数」
$${\bar{x}}$$は標本データの平均、$${s}$$は不偏分散$${s^2}$$の標準偏差です。
$${\cfrac{n}{(n-1)(n-2)} \displaystyle \sum ^n_{i=1} \left( \cfrac{x_i-\bar{x}}{s} \right)^3}$$
■尖度「KURT関数」
$${\cfrac{n(n+1)}{(n-1)(n-2)(n-3)} \displaystyle \sum ^n_{i=1} \left( \cfrac{x_i-\bar{x}}{s} \right)^4 - \cfrac{3(n-1)^2}{(n-2)(n-3)}}$$
■尖度:公式テキスト(§2.6)の計算式
$${\cfrac{E[(X-\mu)^4]}{\sigma^4}-3=\cfrac{1}{n} \displaystyle \sum ^n_{i=1} \left( \cfrac{x_i-\mu}{\sigma} \right)^4-3}$$
それでは各データのヒストグラム、歪度・尖度を見ていきましょう!
データ1:正規分布 $${N(50, 18^2)}$$
きれいな山型です。
正規分布の歪度・尖度はゼロです。

データ2:中央に集中
真ん中の峰が突出しています。尖りが大きいです。
正規分布の形状から大きく乖離しています。
尖度は 4.4 、大きな正の値です。

データセットの値を「値5を1件」「値45を49件」「値55を49件」「値95を1件」に変更してみます。

尖度は 17.5 !
尖りに磨きがかかりました。
ところで、このデータを「値45を50件」「値55を50件」に変更するとどうなるでしょう??

尖度はマイナスになってしまいました。
裾が無くなって、残された中心部が平坦になったからでしょう。
外側のデータが無くなったことで、尖度の値は多く変化しました。
尖度は外れ値に弱いのかもしれません。
データを「値5を1件」「値45を49件」「値55を50件」に変更してみます。

尖度は 17.9。大きな値になります。
どうやら尖度は外れ値の影響を受けやすいようです。
データ3:一様
全ての階級に均等にデータが散らばっています。
この分布は「一様分布」のようです。
尖度は -1.2 。尖りが無くなり、負の値になりました。
ちなみに連続型の一様分布の尖度は - 6/5 です。近似していますね!

データ4:左側に集中
データが左側に偏っていて、右に裾が長い分布です。
歪度は 2.1 。正の値になりました。

データ5:右側に集中
今度は真逆の右側に集中です。
データが右側に偏っていて、左に裾が長い分布です。
歪度は -2.1 。負の値になりました。

データ6、7は$${t}$$分布に関連するデータセットです。
$${t}$$分布に従う乱数を生成して、乱数に一定値を掛けたり足したりしています。
データ6:$${\boldsymbol{t(5)}}$$関連
自由度 5 の$${t}$$分布$${t(5)}$$に従う乱数に対して、10を掛けて5を足したデータセットです。
自由度 5 の$${t}$$分布$${t(5)}$$の理論値は、歪度 0、尖度 6.0 です。

データ7:$${\boldsymbol{t(100)}}$$関連
自由度 100 の$${t}$$分布$${t(100)}$$に従う乱数に対して、10を掛けて5を足したデータセットです。
自由度 100 の$${t}$$分布$${t(100)}$$の理論値は、歪度 0、尖度 0.06 です。

データセットの値をいろいろ変えてみて、グラフの形状、歪度・尖度の変化を楽しんでくださいね。
EXCELサンプルファイルのダウンロード
こちらのリンクからEXCELサンプルファイルをダウンロードできます。
Pythonで作成してみよう!
プログラムコードを読んで、データを流したりデータを変えてみたりして、データを追いかけることで、作表ロジックを把握する方法も効果的でしょう。
サンプルコードを揃えておけば、類似する作表作業を自動化して素早く結果を得ることができます。
今回は、統計検定2級の公式テキスト第2章に登場するさまざまな確率分布の形状と期待値・分散・歪度・尖度を可視化します!
ぜひパラメータを変更して、さまざまな確率分布の形状と数値をご堪能ください!
なお、歪度・尖度の計算にはデータを母集団として扱う場合の計算式を用いています(引数bias=True)。
①インポート
scipy.statsを用いて、確率分布のパラメータに応じた期待値・分散・歪度・尖度を取得したり、確率質量関数、累積分布関数を取得します。
from scipy import stats
from scipy.stats import binom, poisson, geom, uniform, norm, expon, t, chi2, f
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'MS Gothic'
%matplotlib inline②さまざまな確率分布
paramsに各確率分布のパラメータを設定します。
paramsの値を変えてみて、さまざまなパラメータの形状を楽しんでください!
■二項分布 binom
パラメータは [ 試行回数n, 成功確率p ] です。
確率質量関数の値は 確率分布.pmf( xデータ, パラメータ )で取得します。
二項分布の場合は binom.pmf( xデータ, 試行回数n, 成功確率p ) です。
期待値~尖度の値は 確率分布.stats( パラメータ, 取得するモーメントをmvskで指定 )で取得します。
取得するモーメントは、平均:m、分散:v、歪度:s、尖度:kを指定します。
二項分布の場合は binom.stats( 試行回数n, 成功確率p, 取得するモーメント) です。
# 二項分布 binom
params = [[1, 0.1], [5, 0.2], [5, 0.5], [5, 0.8], [10, 0.9]]
x = range(0, 13)
for n, p in params:
y = binom.pmf(x, n, p)
mean, var, skew, kurt = binom.stats(n, p, moments='mvsk')
plt.plot(x, y, label=f'Bin({n},{p}), 期待値:{mean:.2f}, 分散:{var:.2f},'
f'歪度:{skew:.2f}, 尖度:{kurt:.2f}')
plt.title('二項分布')
plt.legend(bbox_to_anchor=(1, -0.1), loc='upper right', borderaxespad=0)
# plt.tight_layout()
# plt.savefig('./binom.png') # グラフ画像ファイルの保存
plt.show()パラメータの組み合わせによって、歪度、尖度はさまざまな値を取ります。
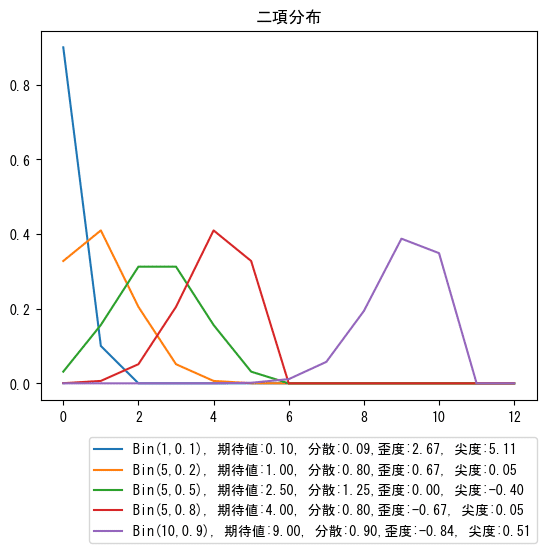
■ポアソン分布 poisson
パラメータは [ 平均 lambda_ ] です。
λの表記 lambda がPythonのlambda関数で使用済みなので _ を付けました。
# ポアソン分布 poisson
params = [1, 3, 5, 10, 20, 30, 50, 80]
x = range(0, 101)
for lambda_ in params:
y = poisson.pmf(x, lambda_)
mean, var, skew, kurt = poisson.stats(lambda_, moments='mvsk')
plt.plot(x, y, label=f'Po({lambda_}), 期待値:{mean}, 分散:{var},'
f'歪度:{skew:.2f}, 尖度:{kurt:.2f}')
plt.title('ポアソン分布')
plt.legend(bbox_to_anchor=(1, -0.1), loc='upper right', borderaxespad=0)
# plt.tight_layout()
# plt.savefig('./poisson.png') # グラフ画像ファイルの保存
plt.show()パラメータ:平均λが大きくなるにつれて、歪度と尖度の値は小さくなっています。

■幾何分布 geom
パラメータは [ 成功確率p ] です。
# 幾何分布 geom : 試行回数xは初めて成功した回数
params = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9]
x = range(0, 21)
for p in params:
y = geom.pmf(x, p)
mean, var, skew, kurt = geom.stats(p, moments='mvsk')
plt.plot(x, y, label=f'Geo({p:.1f}), 期待値:{mean:.1f}, 分散:{var:.1f},'
f'歪度:{skew:.2f}, 尖度:{kurt:.2f}')
plt.title('幾何分布')
plt.legend(bbox_to_anchor=(1, -0.1), loc='upper right', borderaxespad=0)
# plt.tight_layout()
# plt.savefig('./geom.png') # グラフ画像ファイルの保存
plt.show()パラメータ:成功確率pが大きくなるにつれて、グラフの峰が尖り立ち、歪度・尖度の値も大きくなっています。

■連続一様分布 uniform
パラメータは [ 区間下限a, 区間上限b ] です。
確率密度関数の値は 確率分布.pdf( xデータ, パラメータ )で取得します。
連続一様分布の場合は uniform.pdf( xデータ, loc=区間下限a, scale=区間の幅 ) です。
# 連続一様分布 uniform
params = [[-1, 1], [-2, 2], [-3, 3], [-4, 4], [-5, 5], [-6, 6], [-7, 7], [-8, 8]]
x = np.linspace(-10, 10, 1001)
for a, b in params:
y = uniform.pdf(x, loc=a, scale=b-a)
mean, var, skew, kurt = uniform.stats(loc=a, scale=b-a, moments='mvsk')
plt.plot(x, y, label=f'U({a},{b}), 期待値:{mean:.1f}, 分散:{var:.1f},'
f'歪度:{skew:.2f}, 尖度:{kurt:.2f}')
plt.title('連続一様分布')
plt.legend(bbox_to_anchor=(1, -0.1), loc='upper right', borderaxespad=0)
# plt.tight_layout()
# plt.savefig('./uniform.png') # グラフ画像ファイルの保存
plt.show()連続一様分布はパラメータの値にかかわらず、歪度は0、尖度は -6/5 (-1.2)で一定です。

■正規分布 norm
パラメータは [ 平均mu, 標準偏差stddev ] です。
# 正規分布 norm
params = [[0, 1], [1, 2], [2, 3], [4, 5], [5, 10]]
x = np.linspace(-20, 30, 1001)
for mu, stddev in params:
y = norm.pdf(x, loc=mu, scale=stddev)
mean, var, skew, kurt = norm.stats(loc=mu, scale=stddev, moments='mvsk')
plt.plot(x, y, label=f'$N({mu},{stddev}^2)$, 期待値:{mean:.1f}, 分散:{var:.1f},'
f'歪度:{skew:.2f}, 尖度:{kurt:.2f}')
plt.title('正規分布')
plt.legend(bbox_to_anchor=(1, -0.1), loc='upper right', borderaxespad=0)
# plt.tight_layout()
# plt.savefig('./norm.png') # グラフ画像ファイルの保存
plt.show()正規分布の歪度・尖度は0で一定です。
見た目の歪みや尖り具合に騙されてはいけないのです。

■指数分布 expon
パラメータは [ 平均 lambda_ ] です。
scipy.stats.exponでパラメータ:平均λを指定するには、引数 scale=1/λ とします。
# 指数分布 expon
params = [0.1, 0.5, 1, 2, 3, 4, 5]
x = np.linspace(0, 5, 1001)
for lambda_ in params:
y = expon.pdf(x, scale=1/lambda_)
mean, var, skew, kurt = expon.stats(scale=1/lambda_, moments='mvsk')
plt.plot(x, y, label=f'Exp({lambda_:.1f}), 期待値:{mean:.1f}, 分散:{var:.1f},'
f'歪度:{skew:.2f}, 尖度:{kurt:.2f}')
plt.title('指数分布')
plt.legend(bbox_to_anchor=(1, -0.1), loc='upper right', borderaxespad=0)
# plt.tight_layout()
# plt.savefig('./expon.png') # グラフ画像ファイルの保存
plt.show()指数分布はパラメータの値にかかわらず、歪度は2、尖度は 6 で一定です。

■$${t}$$分布 t
パラメータは [ 自由度 df ] です。
# t分布 t
params = [1, 3, 4, 5, 6, 10, 100]
x = np.linspace(-5, 5, 1001)
for df in params:
y = t.pdf(x, df)
mean, var, skew, kurt = t.stats(df, moments='mvsk')
plt.plot(x, y, label=f't({df}), 期待値:{mean:.1f}, 分散:{var:.1f},'
f'歪度:{skew:.2f}, 尖度:{kurt:.2f}')
plt.title('$t$分布')
plt.legend(bbox_to_anchor=(1, -0.1), loc='upper right', borderaxespad=0)
# plt.tight_layout()
# plt.savefig('./t.png') # グラフ画像ファイルの保存
plt.show()きれいなベル型の形状です。歪みがありません。
パラメータ:自由度の値が大きくなるにつれて、尖度の値は小さくなります。正規分布の形状に近づくのです。

■カイ二乗分布 chi2
パラメータは [ 自由度 df ] です。
カイ二乗分布は母分散の区間推定、母分散の検定、適合性の検定、独立性の検定などの場面で大活躍します。
# カイ二乗分布 chi2
params = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
x = np.linspace(0, 30, 1001)
for df in params:
y = chi2.pdf(x, df)
mean, var, skew, kurt = chi2.stats(df, moments='mvsk')
plt.plot(x, y, label=f'$\chi^2$({df}), 期待値:{mean:.1f}, 分散:{var:.1f},'
f'歪度:{skew:.2f}, 尖度:{kurt:.2f}')
plt.title('$\chi^2$分布')
plt.ylim(0, 0.6)
plt.legend(bbox_to_anchor=(1, -0.1), loc='upper right', borderaxespad=0)
# plt.tight_layout()
# plt.savefig('./chi2.png') # グラフ画像ファイルの保存
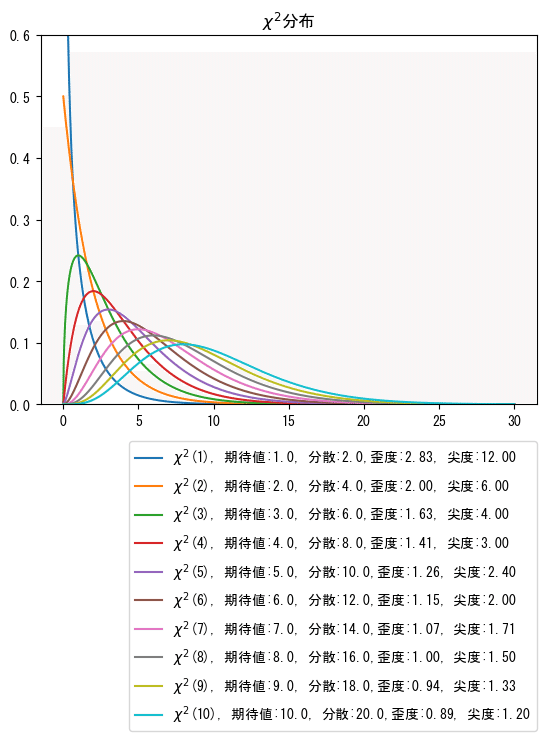
plt.show()パラメータ:自由度の値が大きくなるにつれて、歪度・尖度の値は小さくなります。グラフの形状はなだらかになっています。
■$${F}$$分布 f
自由度$${(\mathrm{df1}, \mathrm{df2})}$$に従う$${F}$$分布$${F(\mathrm{df1}, \mathrm{df2})}$$です。
パラメータは [ 自由度df1, 自由度df2 ] です。
$${F}$$分布は母分散の比の区間推定、母分散の比の検定、分散分析表などで大活躍します。
# F分布 f
params = [[1, 1], [2, 1], [5, 1], [5, 3], [5, 5], [5, 7], [5, 9],
[10, 10], [100, 1000]]
x = np.linspace(0, 3, 1001)
for df1, df2 in params:
y = f.pdf(x, df1, df2)
mean, var, skew, kurt = f.stats(df1, df2, moments='mvsk')
plt.plot(x, y, label=f'$F$({df1},{df2}), 期待値:{mean:.1f}, 分散:{var:.1f},'
f'歪度:{skew:.2f}, 尖度:{kurt:.2f}')
plt.ylim(0, 3)
plt.title('$F$分布')
plt.legend(bbox_to_anchor=(1, -0.1), loc='upper right', borderaxespad=0)
# plt.tight_layout()
# plt.savefig('./f.png') # グラフ画像ファイルの保存
plt.show()
2つのパラメータの相互関係で期待値・分散・歪度・尖度の値は複雑に変わります。
また、$${t}$$分布と同じように、特定の自由度の場合には値なし/無限大になります。
ところで、$${F}$$分布と$${t}$$分布は次のようなつながりを持っています。
$${t}$$が自由度$${n}$$の$${t}$$分布$${t(n)}$$に従うとき、$${t^2}$$は自由度$${(1, n)}$$の$${F}$$分布$${F(1, n)}$$に従います。
③データの歪度・尖度の算出
②のコードでは、歪度・尖度の計算を各確率分布のモーメントから理論値を算出しました。
③のコードでは、EXCELの実践と同じように、scipy.statsのskewとkurtosisを利用して、データセットの各値に基づく歪度・尖度を算出します。
引数bias=Falseを設定すると、EXCELのSKEW.P関数・KURT関数と同等の計算を行います(標本データの扱い)。
引数biasを設定しないと母集団データの扱いで計算します。
# 設定
df = 5 # 自由度
size = 1000 # 乱数の生成数
np.random.seed(5) # 乱数シード
# カイ二乗分布の理論値取得
x = np.linspace(0, 20, 1001)
y = chi2.pdf(x, df=df)
# カイ二乗分布の乱数生成
data = chi2.rvs(df=df, size=size)
# 歪度・尖度の値を取得
y_skew, y_kurt = chi2.stats(df=df, moments='sk') # 理論値
data_skew_pop = stats.skew(data) # 母集団 EXCELの SKEW.P関数と同等
data_kurt_pop = stats.kurtosis(data)
data_skew_sample = stats.skew(data, bias=False) # 標本 EXCELのSKEW関数と同等
data_kurt_sample = stats.kurtosis(data, bias=False) # EXCELのKURT関数と同等
# 歪度・尖度の出力
print(f'自由度 {df}のカイ二乗分布の乱数 {size}件')
print(f'【理論値】 歪度: {y_skew:.5f}, 尖度: {y_kurt:.5f}')
print(f'【母集団】 歪度: {data_skew_pop:.5f}, 尖度: {data_kurt_pop:.5f}')
print(f'【標本】 歪度: {data_skew_sample:.5f}, 尖度: {data_kurt_sample:.5f}')
# プロット
fig, ax = plt.subplots(1, 2, figsize=(8, 4))
# 理論値のプロット
ax[0].plot(x,y)
ax[0].set_title(f'$\chi^2({df})$ 理論値')
# 乱数標本のプロット
bins = np.linspace(0, 20, 21)
freq_num, _, _ = ax[1].hist(data, bins=bins, alpha=0.2)
x2 = bins[:-1] + (bins[1:] - bins[:-1])/2
ax[1].plot(x2, freq_num, c='darkblue')
ax[1].set_title(f'$\chi^2({df})$の乱数の分布')
plt.tight_layout()
# plt.savefig('./chi2_skew_kurt.png') # グラフ画像ファイルの保存
plt.show()

理論値と乱数のグラフの形状はよく似ています。
乱数データに基づいて計算した歪度・尖度は、母集団データ扱い・標本データ扱いの両方が、理論値よりも大きくなっています。
乱数の生成数を増やすと理論値に近づくでしょう。
Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。
おわりに
この記事の執筆時点は、野球の世界大会WBCで日本中が沸いていました。
その影響もあってか、野球のイラストがたくさん出現しました。
じつは今までの記事の中で、この記事の執筆時間が一番長かったです。
書き進めるにつれて取り扱い内容がどんどん膨らみ、結果として、計算式・EXCEL・Pythonの手直し・見直しに多くの時間を割くことになったのです。
時間を使いましたが、書きたいことを盛り込めたので、満足しています。
粘って粘って満塁逆転押し出しフォアボール、みたいな感覚です。

最後までお読みいただきまして、ありがとうございました。
のんびり統計シリーズの記事
次の記事
前の記事
目次
