
シリーズPython⑦ Pythonで体験するベイズ推論 を PyMC Ver.5 で
はじめに
Pythonで体験するベイズ推論の紹介
この記事は書籍「Pythonで体験するベイズ推論: PyMC による MCMC 入門」(森北出版、以下「テキスト」と呼びます)を PyMC Ver.5 で実践したときの留意点を取り扱います。
テキストは、実用的な例題を解いてベイズ推論を実践する素晴らしい書籍です。
例えばメール受信数が時間経過とともに変化したかどうか、などの「例題」が与えられて、例題を解くためのベイズ統計モデリングを行って、MCMC などを用いて解きます。
PyMC によるベイズ統計モデリングの基礎をある程度、学び終えたとき、「ところでベイズって何に使えるんだっけ?」という疑問が浮かび上がることでしょう。
テキストから「こういうことにベイズを使えるんだ!」という答え(実用例)を知ることができます。
ベイズ統計モデリングの基礎を学んでおいて良かった!という幸福感を得られます(個人の意見です)。

■ 注意点は PyMC2 で書かれていること
注意が必要なのは、テキストが PyMC のとても古いバージョン「PyMC2」 を利用している点です。
ありがたいことに、書籍の GitHub に PyMC Ver.5 で動く ipynb の最新コードが掲載(ただし英語)されていて、「ほぼ」最新の PyMC で動かすことができます。
テキストの 「PyMC2 部分のコード」を GitHub の最新コードに読み替えることで、PyMC によるベイズ推論をガッツリ学ぶことができます。
ただし、最新コードの一部にエラーが発生して動かないものがあり、また、最新コードが掲載されていないものがあります。
そこで、この記事では最新コードで問題が生じるケースに焦点をあてて、実際に動く最新コード案の作成にチャレンジいたします。
PyMC の MCMC でガンガン、世の中のパラメータを推論しちゃいましょう!!!

まえがき
この記事は、出典に記載の書籍に掲載された文章及びコードを引用し、適宜、掲載文章とコードを改変して書いています。
PyMC Ver.5 のコードは「見つけることができた範囲内の処理内容」であり、処理の正確性は担保しておりません。
誤りや改善点がありましたら、ぜひ教えてください。
【出典】
「Pythonで体験するベイズ推論: PyMC による MCMC 入門」(第1版第6刷、Cameron Davidson-Pilon 著、玉木徹 訳、森北出版)
■ お品書き
章単位に区切って、コード案と出力イメージを記載いたします。
コード案はできる限り PyMC Ver.5 的な書き方を心がけます。
GitHubに掲載されたファイル名「~PyMC_current.ipynb」のコードを「最新コード」と呼びます。
バージョン情報
・Python : 3.11.5
・PyMC : 5.8.2
・PyTensor : 2.16.2
・Arviz : 0.16.1
では、ベイズ統計と PyMC の新たな旅へ出発しましょう🚀
第1章 ベイズ推論の考え方
■ 対象コード
「付録」の「二つの変化点への拡張」(26~30ページ)のコードを取り扱います。
■ テキストの特徴
1.4.1「例題:メッセージ数に変化はあるか?」では、筆者の毎日の「メッセージ受信数」が時間が経つにつれて変化しているかどうか、および、変化しているならばいつ=$${\tau}$$日目に変化したのかについて、ベイズ推論で明らかにします。
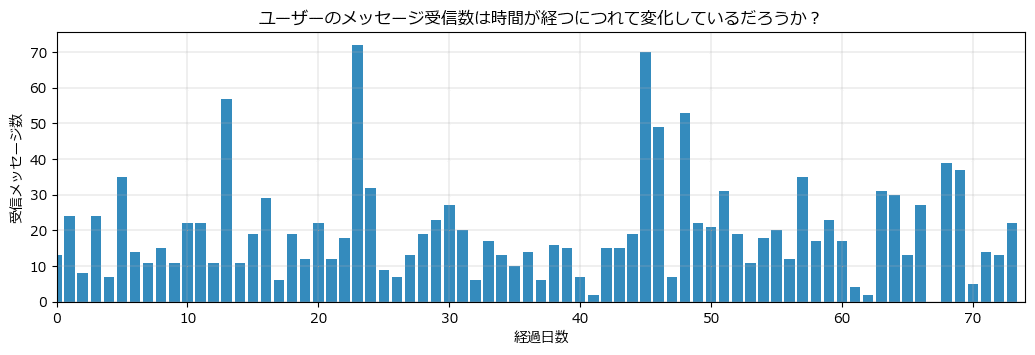
本編では「1つの変化点($${\tau}$$は1つ)」と仮定してモデリングしています。
一方で、付録では「2つの変化点($${\tau}$$は2つ)」をもつように、モデルを拡張しています。
■ 課題
GitHub には、付録の「2つの変化点」モデルの最新コードの掲載がありません。
そこで、この記事にて最新コード案の作成を試みます。

追加インポート
arviz をインポートします。
import arviz as azPyMC のモデル定義
さっそく PyMC のモデルを定義しましょう。
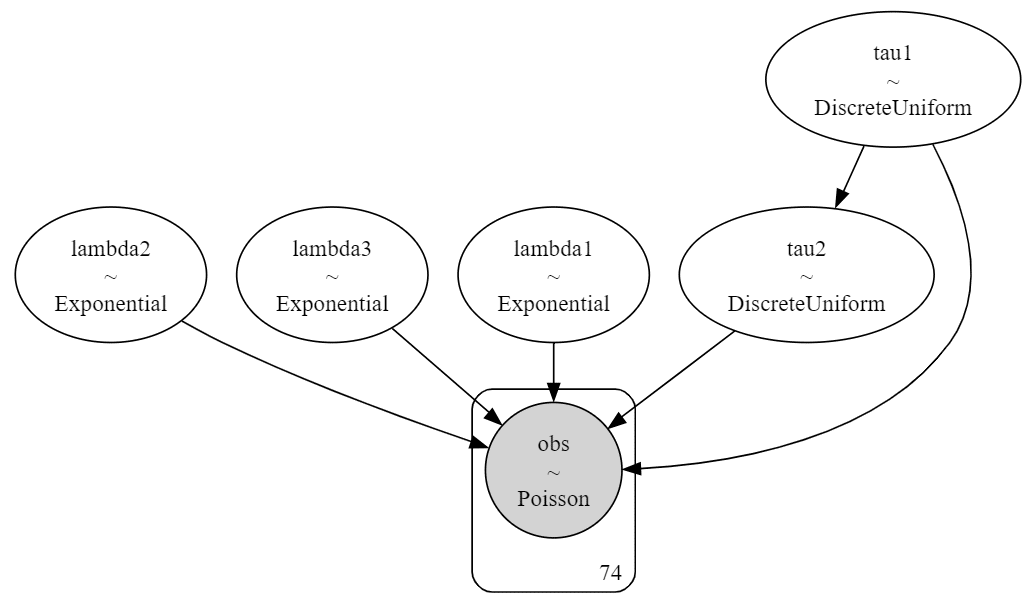
2つの$${\tau}$$で区切られた3つの間隔ごとに、ポアソン分布の平均パラメータ$${\lambda}$$が異なります
$${\lambda}$$は指数分布に従うと想定しています。
テキストの PyMC2 のコードと、付録の前までの箇所の最新コードを参考にして作りました。
なお、変数名に「_」(アンダースコア)を使わないようにしています。
モデルの表示時に KaTeX エラーの発生を回避するためです。
### モデルの定義
with pm.Model() as model:
### 事前分布
alpha = 1.0 / count_data.mean()
lambda1 = pm.Exponential('lambda1',lam=alpha)
lambda2 = pm.Exponential('lambda2',lam=alpha)
lambda3 = pm.Exponential('lambda3',lam=alpha)
tau1 = pm.DiscreteUniform('tau1', lower=0, upper=n_count_data - 1)
tau2 = pm.DiscreteUniform('tau2', lower=tau1, upper=n_count_data)
### lambdaの定義
# index
idx = np.arange(n_count_data)
# tau1より前のλはλ1、tau1からtau2の間はλ2、tau2から後ろのλはλ3
lambda_ = pm.math.switch(idx < tau1 , lambda1,
pm.math.switch(idx < tau2, lambda2, lambda3))
### 尤度
obs = pm.Poisson('obs', lambda_, observed=count_data)モデルの表示
# モデルの表示
model【実行結果】

モデルの可視化
# モデルの可視化
pm.model_to_graphviz(model)【実行結果】
事後分布からのサンプリング
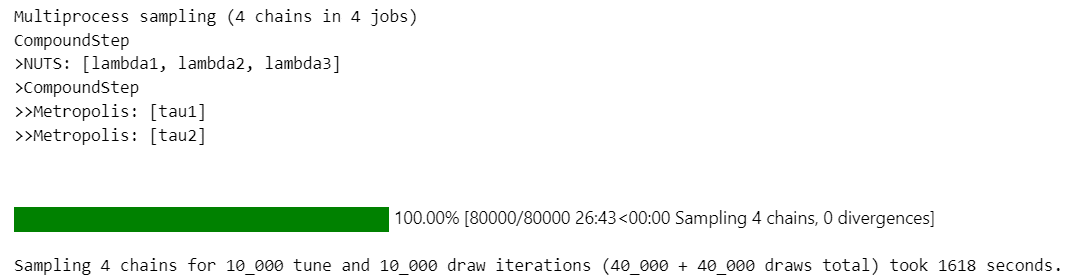
chain:4 ×draw:10000 = 40000 個のサンプリングを行います。
### 事後分布からのサンプリング
with model:
idata = pm.sample(draws=10000, tune=10000, chains=4,
target_accept=0.9, random_seed=123)【実行結果】
26分ほどの時間がかかりました。
また、RuntimeWarning が発生しています(掲載省略)。
推論データの要約統計情報の表示
### 推論データの要約統計情報の表示
pm.summary(idata)【実行結果】
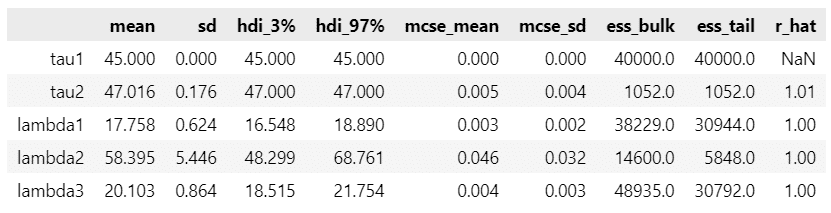
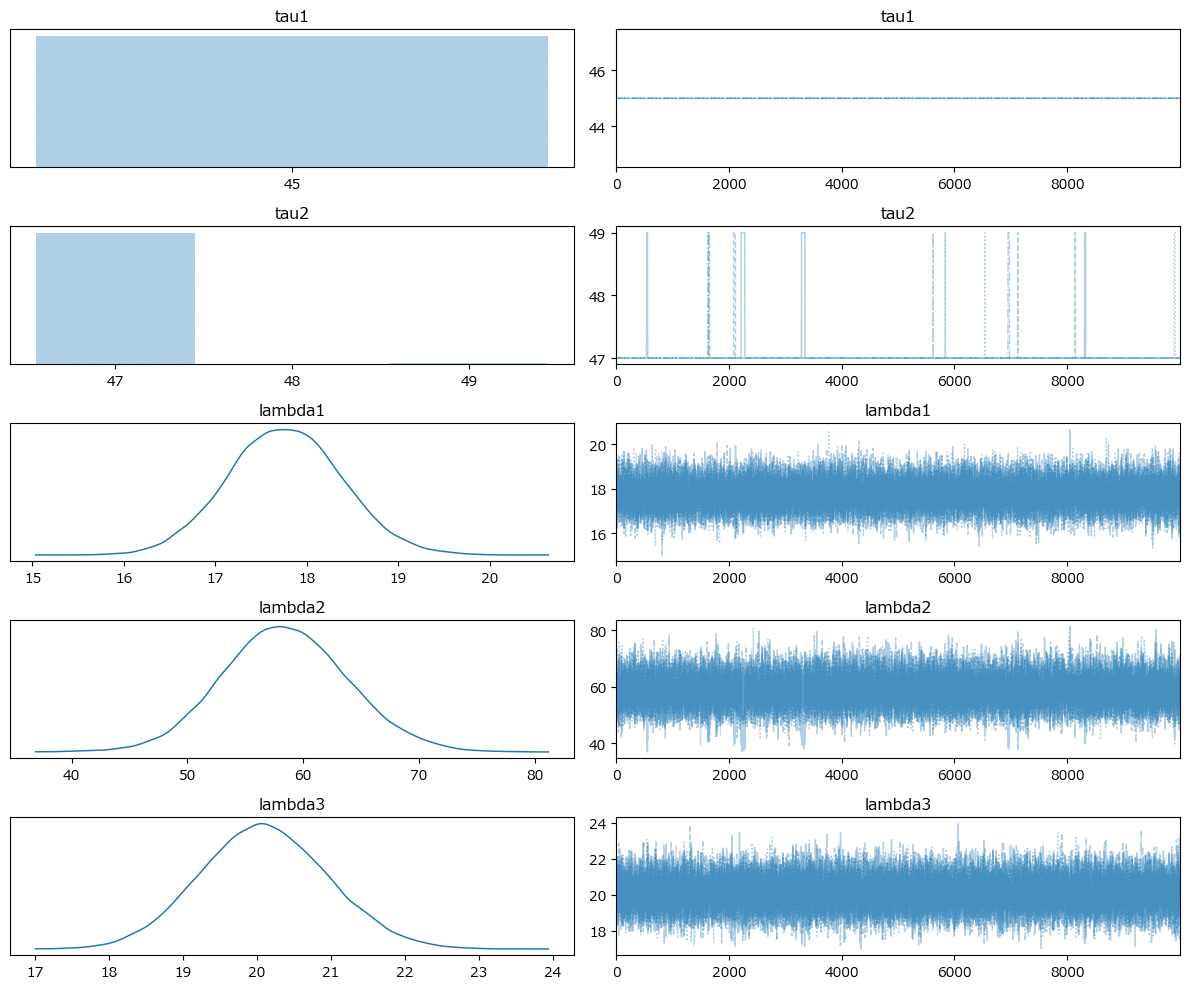
トレースプロットの描画
### トレースプロットの描画
pm.plot_trace(idata, combined=True)
plt.tight_layout();【実行結果】
$${\tau_1, \tau_2}$$はほぼ一定の値が得られたようです。
3つの$${\lambda}$$については、1峰の正規分布のような形状で取得できたようです。
事後分布プロットの描画
### 事後分布プロットの描画
pm.plot_posterior(idata, var_names=['tau1', 'tau2']);
pm.plot_posterior(idata, var_names=['lambda1', 'lambda2','lambda3']);【実行結果】
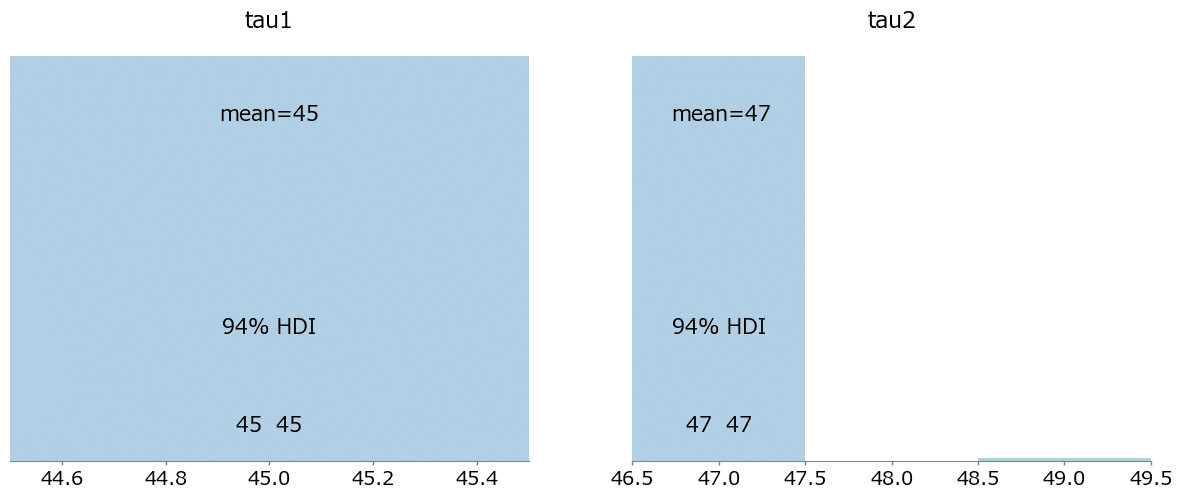
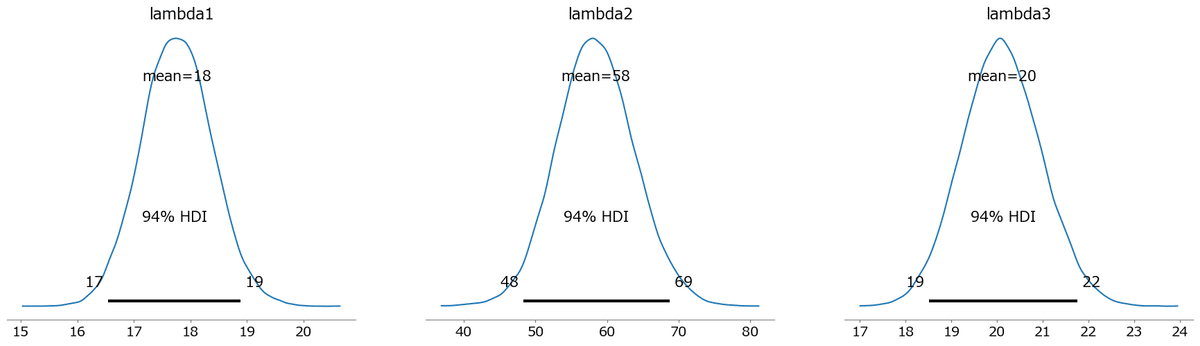
テキストの事後分布プロットの描画
テキストのコードをほぼ踏襲しています。
コード冒頭では、arviz の extract を利用して、推論データ「idata」(テキストでは trace)から posterior グループを抜き出しました。
arviz を利用しない場合は「 idata.posterior.lambda1.data.flatten() 」など、idata の posterior グループにアクセスするコードで対応することになるでしょう。
### プロット
# traceデータをextractする
idata_ext = az.extract(idata)
# パラメータの事後分布のサンプルを各変数に代入
lambda_1_samples = idata_ext.lambda1.values
lambda_2_samples = idata_ext.lambda2.values
lambda_3_samples = idata_ext.lambda3.values
tau_1_samples = idata_ext.tau1.values
tau_2_samples = idata_ext.tau2.values
# プロットの準備
fig, ax = plt.subplots(5, 1, figsize=(10, 15))
# λ1のヒストグラムのプロット
ax[0].hist(lambda_1_samples, histtype='stepfilled', bins=30, alpha=0.85,
color='steelblue', density='normed', label=r'$\lambda_1$の事後確率')
ax[0].set_ylim([0, 1])
ax[0].set_xlabel(r'$\lambda_1$の値')
ax[0].set_ylabel('確率密度')
ax[0].legend(loc='upper left')
# λ2のヒストグラムのプロット
ax[1].hist(lambda_2_samples, histtype='stepfilled', bins=30, alpha=0.85,
color='darkorange', density='normed', label=r'$\lambda_2$の事後確率')
ax[1].set_ylim([0, 1])
ax[1].set_xlabel(r'$\lambda_2$の値')
ax[1].set_ylabel('確率密度')
ax[1].legend(loc='upper left')
# λ3のヒストグラムのプロット
ax[2].hist(lambda_3_samples, histtype='stepfilled', bins=30, alpha=0.85,
color='darkgreen', density='normed', label=r'$\lambda_3$の事後確率')
ax[2].set_ylim([0, 1])
ax[2].set_xlabel(r'$\lambda_3$の値')
ax[2].set_ylabel('確率密度')
ax[2].legend(loc='upper left')
# τ1のヒストグラムのプロット
w = 1.0 / tau_1_samples.shape[0] * np.ones_like(tau_1_samples)
ax[3].hist(tau_1_samples, bins=n_count_data, alpha=1,
color='gray', weights=w, rwidth=2, label=r'$\tau_1$の事後確率')
ax[3].set_xlim([40, 50])
ax[3].set_ylim([0, 1])
ax[3].set_xlabel(r'経過日数')
ax[3].set_ylabel('確率')
ax[3].legend(loc='upper left')
# τ2のヒストグラムのプロット
w = 1.0 / tau_2_samples.shape[0] * np.ones_like(tau_2_samples)
ax[4].hist(tau_2_samples, bins=n_count_data, alpha=1,
color='purple', weights=w, rwidth=2, label=r'$\tau_2$の事後確率')
ax[4].set_xlim([40, 50])
ax[4].set_ylim([0, 1])
ax[4].set_xlabel(r'経過日数')
ax[4].set_ylabel('確率')
ax[4].legend(loc='upper left')
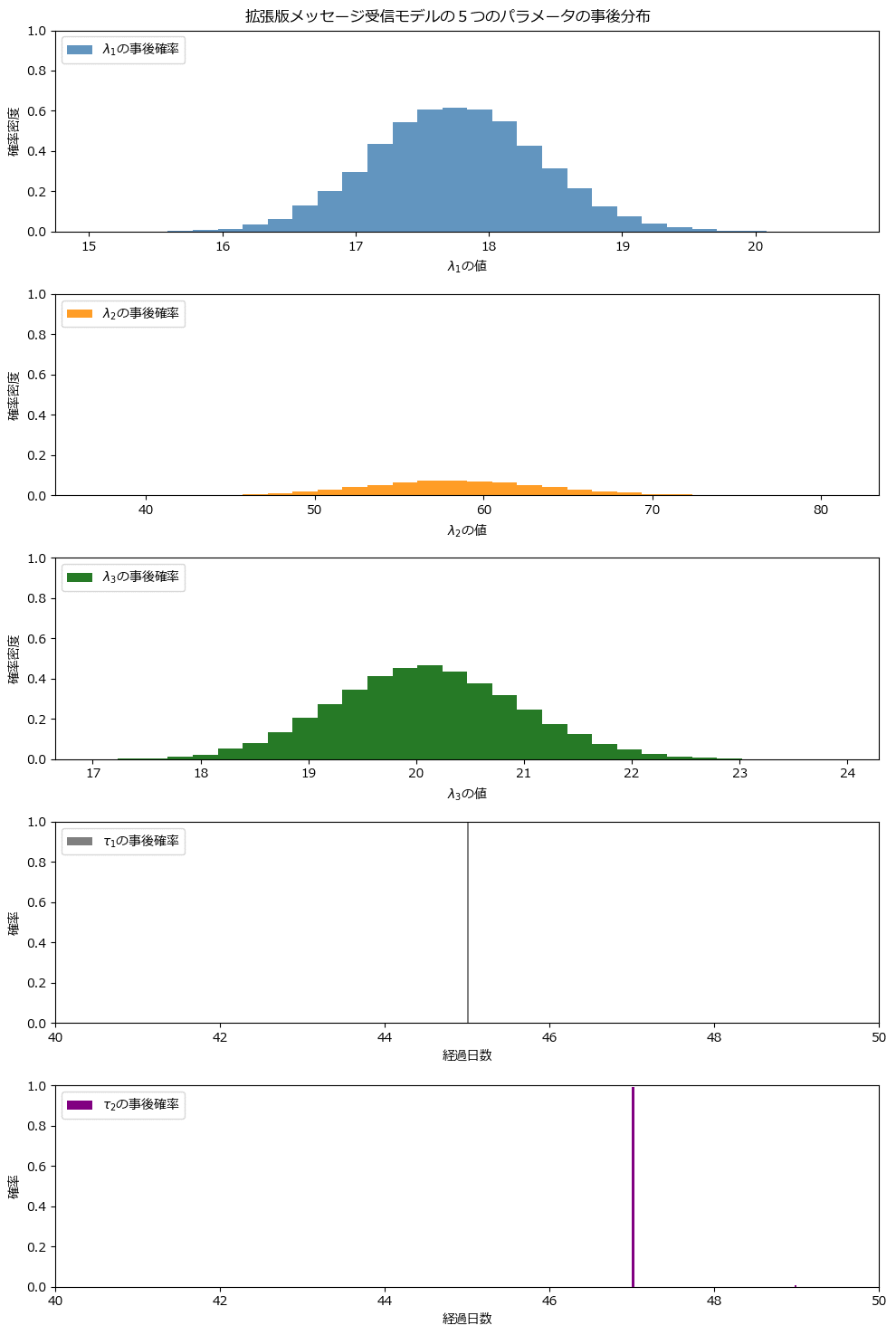
plt.suptitle('拡張版メッセージ受信モデルの5つのパラメータの事後分布')
plt.tight_layout()
plt.show()【実行結果】
トレースプロットの形状とよく似ています(あたりまえ!?)。
変化点($${\tau_i, \tau_2}$$)が 45 日目と 47 日目に現れています。
第4章 偉大な定理、登場
■ 対象コード
「4.3.3 例題:Redditコメントをソートする」~「4.3.5 でも計算が遅すぎる!」(テキスト129~140ページ)のコードを取り扱います。
■ テキストの特徴
アメリカの掲示板サイト「Reddit」に寄せられた「コメント」には「いいね」(upvote)と「わるいね」(downvote)が投票されています。
このコメントと投票のデータを用いて、ベイズ推論で「コメントに対する真のいいね比率」を推定し、ベストなコメントを探ります。
(参考)Reddit 日本語版サイトのリンク

■ 課題
最新コードでは、「praw」ライブラリを用いた Python スクリプト「top_showerthoughts_submissions.py」を利用して、Reddit サイトからコメントデータをダウンロードします。
【最新コード】
%run top_showerthoughts_submissions.py 2
print("Post contents: \n")
print(top_post)しかし私の PC で実行したところ、エラーが発生して、Reddit からコメントデータをダウンロードできませんでした。
エラーの原因は、Python スクリプトによるコメント検索の際に用いる検索ワード「BayesianMethodsForHackers」が Reddit で見つからないことのようです。
ブラウザで Reddit 内の検索をしたところ、たしかに「BayesianMethodsForHackers」は見つかりませんでした。
もしかすると、テキストのコードで利用したいコメントデータが既に Reddit から削除されたのかもしれません。
そこで暫定的な対処として、コメントデータに似せたダミーデータを作成して、PyMC を続行・満喫する作戦に移りました。

ダミーデータの作成
上述の最新コードに代えて、このコードを実行して、ダミーのコメントデータ(正確には投票データ)を作成します。
一様分布$${\text{Uniform}(0, 100)}$$から2次元で50個の整数乱数を、一様分布$${\text{Uniform}(0, 10)}$$から2次元で50個の整数乱数を、それぞれ取得して、合計100個の[いいね数, わるいね数]の組み合わせをもつ NumPy 配列を作成しています。
なお、ダミーデータには「コメント文章」を含めていないので、以降のコードでは、コメント文章を都度都度、作り込んでいます。
# 一様乱数で擬似的に投票データを生成、コメントは生成しない
# 50投票について、いいね、わるいねの数が0~100になるように乱数を取得
votes1 = np.random.randint(0, 100, size=(50, 2))
# 50投票について、いいね、わるいねの数が0~10になるように乱数を取得
votes2 = np.random.randint(0, 10, size=(50, 2))
# 2つの投票を結合
votes = np.concatenate([votes1, votes2])
votes【実行結果】

ランダムに4つのコメントを選んで投票数を表示
このコードで選択した4つのコメントデータが、以降のコードに使われます。
実行結果の[いいね数, わるいね数]が少ないものと多いものを含むように確認をしながら、コード実行を試行してください。
なお、ダミーデータにはコメント文章を含んでいないので、適当なテキストを表示するように最新コードを改造しています。
# 取得した(つもりの)コメントから4つをランダムに選び、投票数を表示する
# コメントの数(100件)
n_submissions = len(votes)
# ランダムに選んだ4つのコメントのINDEX
submissions = np.random.randint(n_submissions, size=4)
print(f'いくつかのコメント(全{n_submissions}件)\n', '-'*30)
for i in submissions:
print(f'No.{i+1} コメント文は省略・・・')
print('いいね/わるいね: ', votes[i, :], '\n')【実行結果】

事後分布からいいね比率をサンプリングする関数の定義
( PyMC のモデル定義を含む)
最新コードをそのまま使えます。
コード説明のコメントを追加しました。
import pymc as pm
# 事後分布からいいね比率をサンプリングする関数の定義
def posterior_upvote_ratio(upvotes, downvotes, samples=15000):
'''
引数
upvotes: ある特定のコメントについてのupvoteの数
downvotes: ある特定のコメントについてのdownvoteの数
samples: 戻り値となる事後分布からのサンプル数(一様事前分布を仮定する)
'''
# 試行回数=いいねの数+わるいねの数
N = upvotes + downvotes
# PyMCのモデルの定義・事後分布からのサンプリング
with pm.Model() as model:
# いいね比率(=p)の事前分布
upvoteRatio = pm.Uniform('upvoteRatio', 0, 1)
# いいね投票数の尤度:二項分布
obs = pm.Binomial('obs', N, upvoteRatio, observed=upvotes)
# いいね比率の事後分布からのサンプリング
idata = pm.sample(draws=samples, tune=5000, chains=1, step=pm.NUTS())
# 戻り値:事後分布からのいいね比率のサンプル
return idata.posterior.upvoteRatio.data.T上記の関数に含まれている model の内容を可視化しましょう。
votes に含む1番目のコメントデータ(votes[0, :])のケースです。
# モデルの表示のためにモデルを定義する
upvotes = votes[0, 0]
downvotes = votes[0, 1]
N = upvotes + downvotes
with pm.Model() as model:
# いいね比率(=p)の事前分布
upvoteRatio = pm.Uniform('upvoteRatio', 0, 1)
# いいね投票数の尤度:二項分布
obs = pm.Binomial('obs', N, upvoteRatio, observed=upvotes)
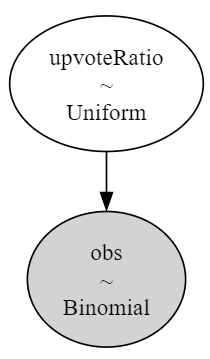
# モデルの表示と可視化
display(model)
pm.model_to_graphviz(model)【実行結果】

事後分布の取得とプロット
先に定義した関数を用いて、事後分布からのサンプリングを実行し、取得できた「いいね比率」をプロットします。
ダミーデータにはコメント文章を含んでいないので、適当なテキストを表示するように最新コードを改造しています。
### 事後分布の取とプロット
# 初期値設定
posteriors = []
colors = ['steelblue', 'tomato', 'darkgreen', 'darkorange']
# 描画
plt.figure(figsize=(12, 8))
for i in range(len(submissions)):
# コメントのINDEXを取得
j = submissions[i]
# j番目のコメントのいいね/わるいねの数を観測値にして事後分布のMCMCサンプルを取得
posteriors.append(posterior_upvote_ratio(votes[j, 0], votes[j, 1]))
# 「いいね比率」の事後分布の描画
plt.hist(posteriors[i], bins=10, density=True, histtype='step',
color=colors[i%5], alpha=0.9, lw=3,
label=f'No.{j} ({votes[j, 0]} いいね :{votes[j, 1]} わるいね)'
'コメント省略...')
plt.hist(posteriors[i], bins=10, density=True, histtype='stepfilled',
color=colors[i], alpha=0.2, lw=3)
plt.xlim(0, 1)
plt.xlabel('いいね比率')
plt.ylabel('確率密度')
plt.title('それぞれのコメントに対するいいね比率の事後分布')
plt.legend()
plt.show()【実行結果】
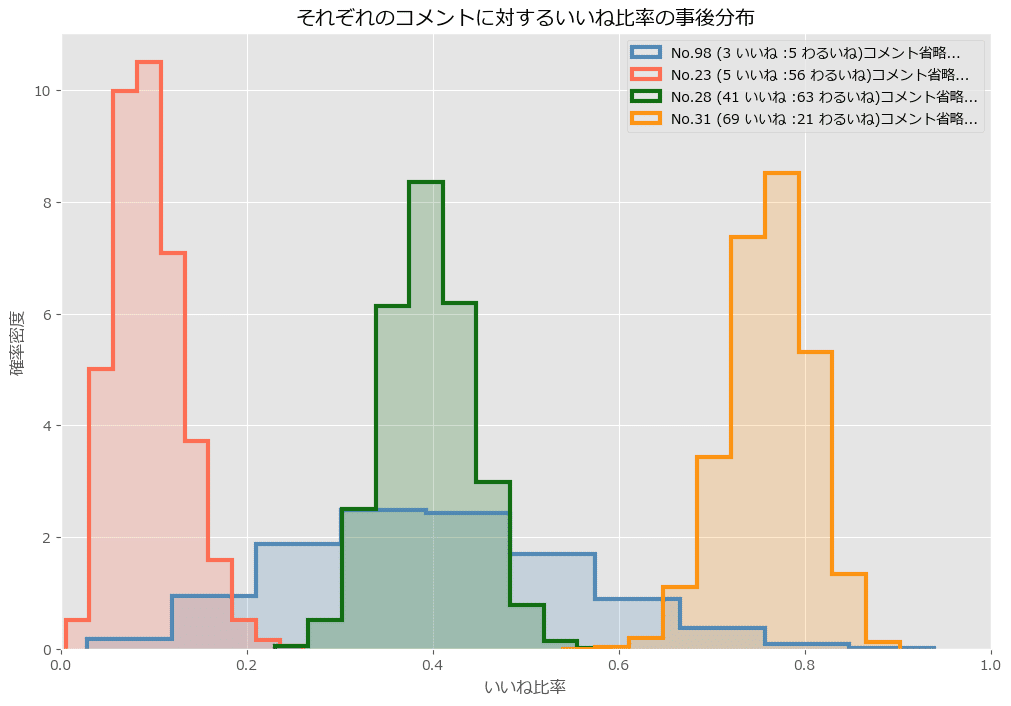
95%信用下限を表示したプロットの描画
ダミーデータにはコメント文章を含んでいないので、適当なテキストを表示するように最新コードを改造しています。
### 95%信用下限を表示したプロットを描画する
# 初期値設定
N = posteriors[0].shape[0] # 事後分布のサンプルの数15000
lower_limits = [] # 4つのいいね比率の95%信用下限を格納するリスト
plt.figure(figsize=(14, 8))
for i in range(len(submissions)):
# コメントのINDEXを取得
j = submissions[i]
# コメントのINDEXに合致する「いいね比率」の事後分布を描画
plt.hist(posteriors[i], bins=20, density=True, histtype='step',
color=colors[i], alpha=0.9, lw=3,
label=f'No.{j} ({votes[j, 0]} いいね :{votes[j, 1]} わるいね)'
'コメント省略...')
plt.hist(posteriors[i], bins=20, density=True, histtype='stepfilled',
color=colors[i], alpha=0.2, lw=3)
# 95%信用下限を計算して垂直線を描画
v = np.sort(posteriors[i])[int(0.05*N)]
plt.vlines(v, 0, 10, color=colors[i], ls='--', lw=3)
# 95%信用下限の値をリストに格納
lower_limits.append(v)
plt.xlabel('いいね比率')
plt.ylabel('確率密度')
plt.title('それぞれのコメントに対するいいね比率の事後分布')
plt.legend(loc='upper left')
order = np.argsort(-np.array(lower_limits))
print(order, lower_limits)
plt.show()【実行結果】

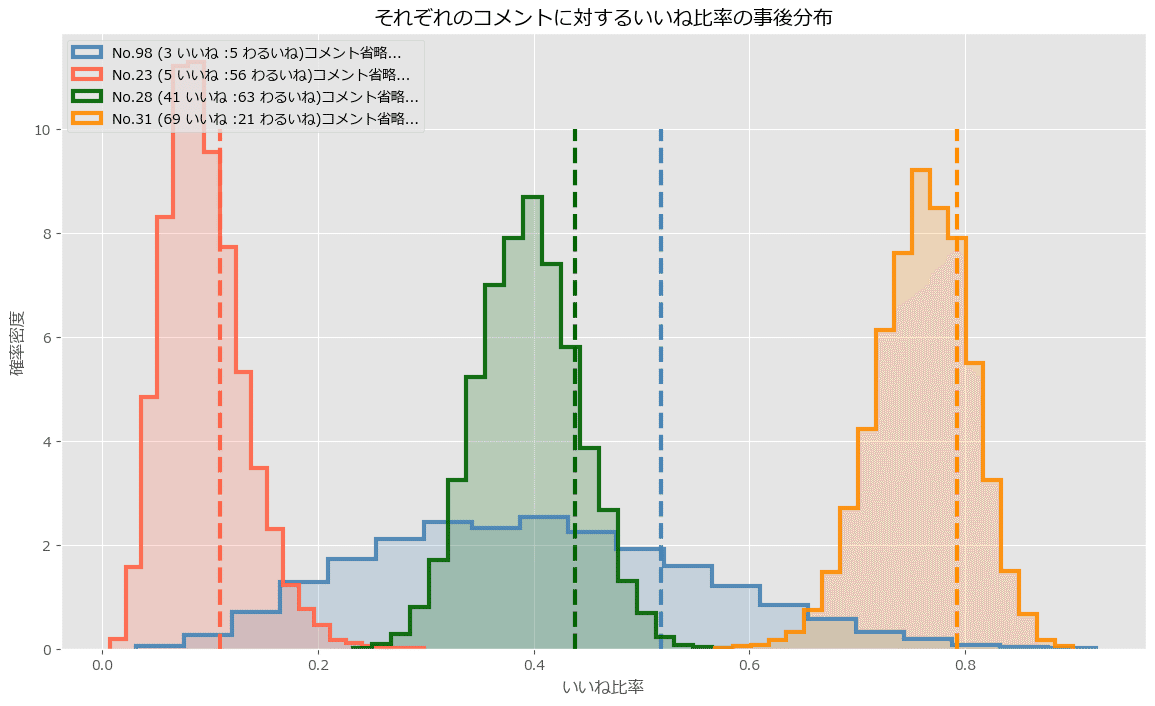
信用下限の近似下界でソートしてトップ40を表示
ダミーデータにはコメント文章を含んでいないので、適当なテキストを表示するように最新コードを改造しています。
### 信用下限の近似下界でソートしてトップ40を表示
# 信用下限の近似下界を求める関数
def intervals(u, d):
a = 1 + u
b = 1 + d
mu = a/(a+b)
std_err = 1.65*np.sqrt((a*b)/((a+b)**2 * (a+b+1)))
return (mu, std_err)
# 近似下界の算出
print('近似的な下界')
posterior_mean, std_err = intervals(votes[:, 0], votes[:, 1])
lb = posterior_mean - std_err
print(lb)
# 近似下界でソートしてトップ40を表示
print('\n近似下界でソートしたトップ40\n')
order = np.argsort(-lb)
ordered_contents = []
# コメント省略に対応した表示コード
for i in order[:40]:
ordered_contents.append(f'No.{i}: コメント省略')
print(votes[i, 0], votes[i, 1], f'No.{i}: コメント省略')
print('-'*20)【実行結果】

コメントトップ40の描画
最新コードをそのまま使えます。
コード説明のコメントを追加しました。
### コメントトップ40の描画
# コメントトップ40データを降順ソートしてリバースオーダーr_orderに格納
r_order = order[::-1][-40:]
# プロットの準備
plt.figure(figsize=(14, 8))
# 近似下界の平均値をドット・標準偏差をエラーバーにして描画
plt.errorbar(posterior_mean[r_order], np.arange(len(r_order)),
xerr=std_err[r_order], capsize=0, fmt='o', color='steelblue')
plt.xlim(0.3, 1)
plt.yticks(np.arange(len(r_order)-1, -1, -1),
map(lambda x: x[:30].replace('\n', ''), ordered_contents));【実行結果】
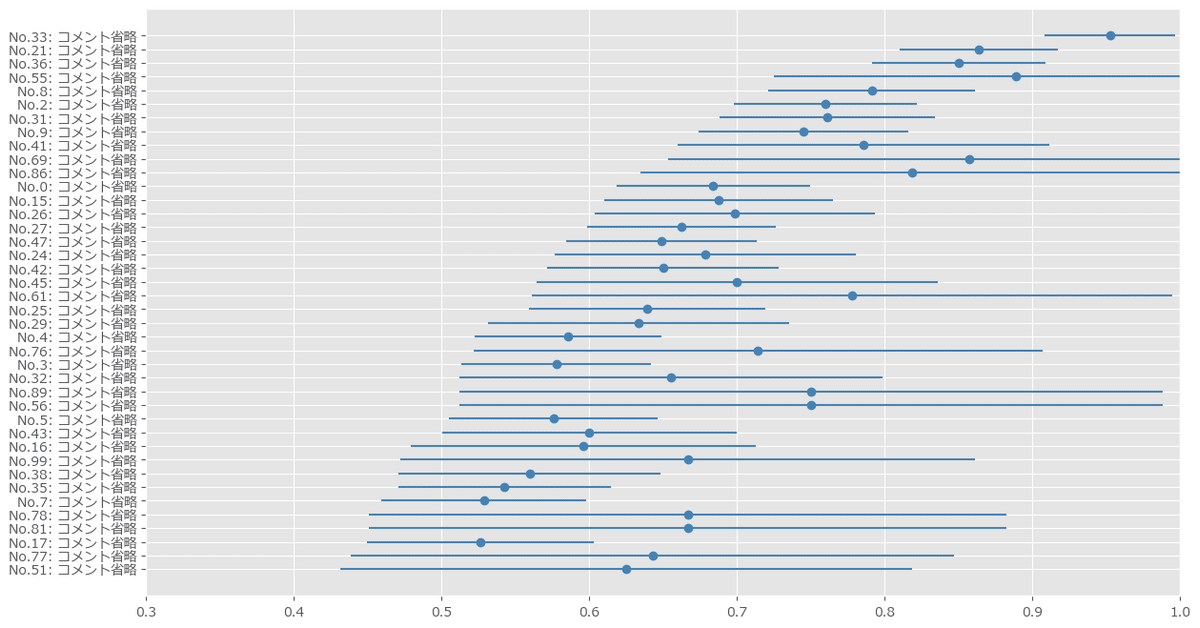
信用下限の近似値でソートすることによって、点推定(平均値、図の点)よりも妥当性が高そうな「いいね比率」の上位を表示できました。
第6章 事前分布をハッキリさせよう
その1:株売買の収益
■ 対象コード
「6.5.2 例題:株売買の収益」(テキスト201~209ページ)の「株価データをダウンロードする」コードを取り扱います。
■ テキストの特徴
アップル(AAPL)、グーグル(GOOG)※、テスラモーターズ(TSLA)、アマゾン(AMZN)の4銘柄の株価を Yahoo! からダウンロードして、期待日次リターンを推測します。
モデリングの精度を上げる方策として、各銘柄のリターンの共分散行列を考慮する目的で、ウィシャート分布を利用します。
※ グーグル社がアルファベット社に変わる前が分析対象期間と思われます。

■ 課題
テキストのコード、および、GitHub の新規コードでは、株価データのダウンロード処理でエラーが発生して、株価データを取得できません。
具体的には、新規コードで利用するデータ取得ライブラリ「pandas_datareader」の「get_data_yahoo」にて Yahoo! にアクセスする処理で、次のエラーが発生します。
TypeError: string indices must be integers, not 'str'
このままでは、株価リターンの推論を動かして学べないです。。。
ということで、pandas_datareader に代わる別のライブラリに置き換えて、株価データを取得します!
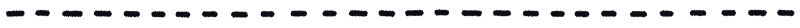
インストール
Yahoo! ファイナンスにアクセスするライブラリ「yfinance」をインストールします。
### yfinance のインストール
# pipの場合
pip install yfinance
# condaの場合
conda install -c conda-forge yfinance インポート
yfinance をインポートします。
pandas_datareader のインポートは不要です。
import pandas as pd
# ★★修正箇所
# import pandas_datareader as pdr
import yfinance as yfin株価データのダウンロード
新規コードのうち、★★印の箇所を変更します。
### 株価データのダウンロード
## 初期値設定
# 過去100日で打ち切る
n_observations = 100
# 銘柄リストの設定:アップル、グーグル、テスラ、アマゾン
stocks = ['AAPL', 'GOOG', 'TSLA', 'AMZN']
# データ取得開始日~終了日の設定
startdate = '2012-09-01'
enddate = '2015-04-27'
# データフレームの初期化
stock_closes = pd.DataFrame()
## 4銘柄の株価終値データ取得処理 by yfinance.download
for stock in stocks:
# ★★修正箇所
# data = pdr.get_data_yahoo(stock, start=startdate, end=enddate)['Close']
data = yfin.download(stock, start=startdate, end=enddate)['Close']
stock_closes[stock] = data
## 株価終値データの整形
# 株価終値データの並び替え
stock_closes = stock_closes[::-1]
# 日次リターン率の算出:pandas.pct_change利用
stock_returns = stock_closes.pct_change()[1:][-n_observations:]
# 日付INDEXの取得
dates = stock_returns.index.to_list()【実行結果】

株価終値データ、日次リターン率データの内容確認
テキストや新規コードには無いですが、データの内容を軽く見ておきます。
以後の処理では日次リターン率データ「stock_returns」をよく使います。
### 株価終値データ、日次リターン率データの表示
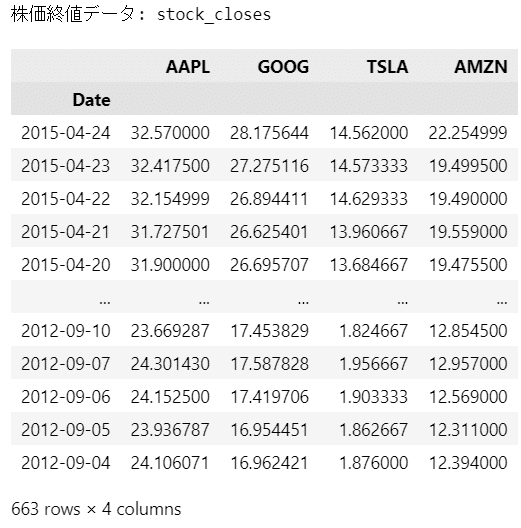
print('株価終値データ: stock_closes')
display(stock_closes)
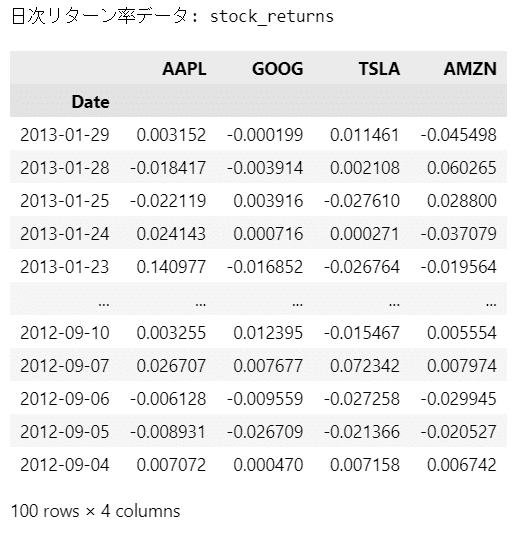
print('日次リターン率データ: stock_returns')
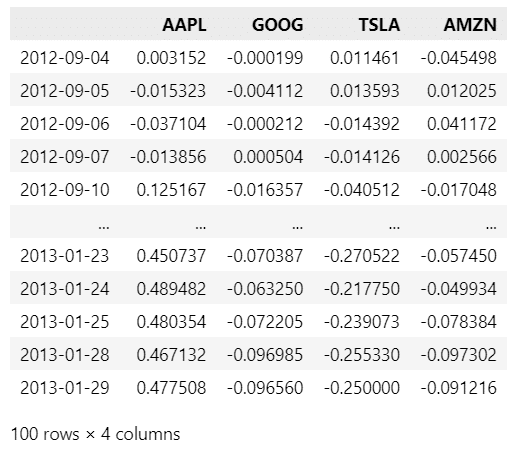
display(stock_returns)【実行結果】
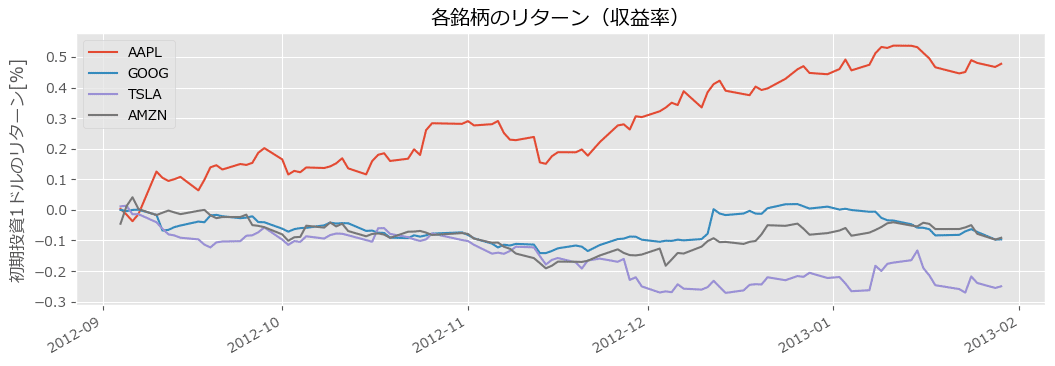
株価終値データの可視化
新規コードからの変更はありません。
グラフの形状が若干、新規コードと異なるのが気になりますが、深追いせず、このまま続けましょう。
# 日次リターン率の累積積dfの作成
cum_returns = np.cumprod(1 + stock_returns) - 1
# 日付INDEXを累積積dfのINDEXにセット
cum_returns.index = dates[::-1]
# 日次リターン率の累積積dfのプロット
cum_returns.plot(figsize=(12.5, 4))
plt.title('各銘柄のリターン(収益率)')
plt.ylabel('初期投資1ドルのリターン[%]')
plt.legend(loc='upper left')
plt.show()【実行結果】
日次リターン率の累積積データの表示
上のコードで作成した日次リターン率の累積積dfを表示します。
### 日次リターン率の累積積dfの表示
display(cum_returns)【実行結果】
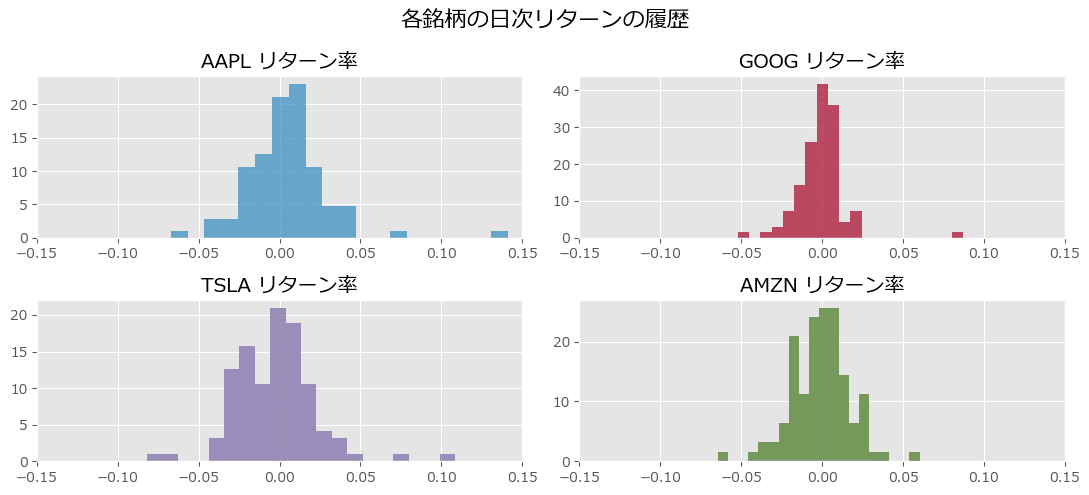
各銘柄の日次リターン率データのヒストグラムの描画
新規コードからの変更はありません。
### 各銘柄の日次リターン率のヒストグラムのプロット
plt.figure(figsize=(11, 5))
for i, _stock in enumerate(stocks):
plt.subplot(2, 2, i+1)
plt.hist(stock_returns[_stock], bins=20, density=True,
histtype='stepfilled', color=colors[i], alpha=0.7)
plt.title(_stock + ' リターン率')
plt.xlim(-0.15, 0.15)
plt.suptitle('各銘柄の日次リターンの履歴', fontsize=16)
plt.tight_layout()
plt.show()【実行結果】
PyMC モデルの定義
新規コードからの変更はほぼありません。
コメントによる説明を付加したり、バラバラの model 定義コードをひとまとめにしたり、graphviz によるモデルの可視化を追加しています。
### インポート
import pymc as pm### 初期値の設定
# 事前分布のパラメータ設定(ファンドマネージャーによるパラメータμ, σ)
prior_mu = np.array([x[0] for x in expert_prior_params.values()])
prior_std = np.array([x[1] for x in expert_prior_params.values()])
# 4銘柄の株価の共分散を取得、ウィシャート分布の初期値に利用
init = stock_returns.cov()### モデルの定義
with pm.Model() as model:
# 事前分布:共分散
covariance = pm.WishartBartlett('covariance', np.diag(prior_std**2), 10,
initval=init)
# 事前分布:平均
returns = pm.Normal('returns', mu=prior_mu, sigma=1, shape=4)
# 尤度
obs = pm.MvNormal('obs', mu=returns, cov=covariance, observed=stock_returns)【実行結果】
「_」付きの PyMC 変数が生成されたので、KaTeX が受け付けてくれず、「model」の表示ができなくなりました(泣)
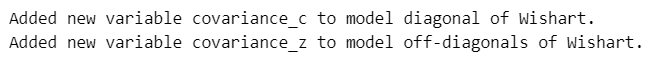
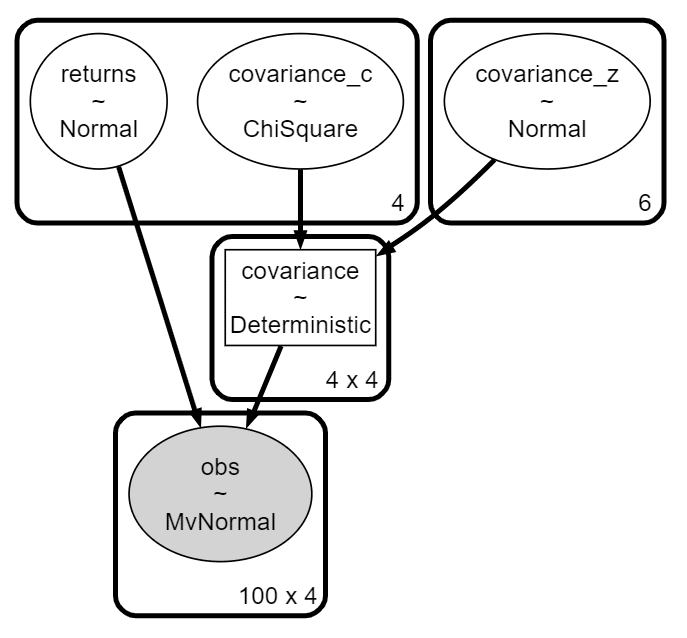
# モデルの可視化
pm.model_to_graphviz(model)【実行結果】
共分散_c が従う分布に「カイ二乗分布」が指定されたようです。
事後分布からのサンプリング
chain が 1本なので、ワーニングがでます。
サンプルデータについて、要約統計情報、トレースプロット、事後分布プロットを確認しましょう。
# 事前分布からのサンプリング
with model:
idata = pm.sample(5000, tune=1000, chains=1, random_seed=123)【実行結果】
そこそこ時間がかかりました。
※後日談:nuts_sampler に numpyro を利用したら噂通り爆速でした!
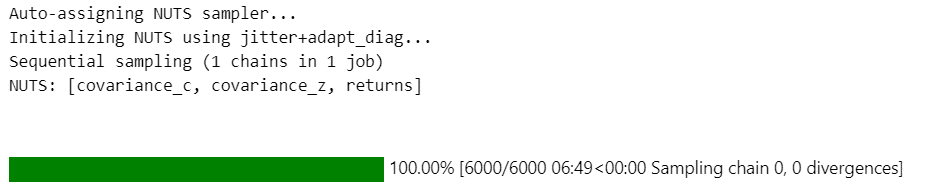
# returnsの要約統計情報の表示
pm.summary(idata, var_names=['returns'])【実行結果】
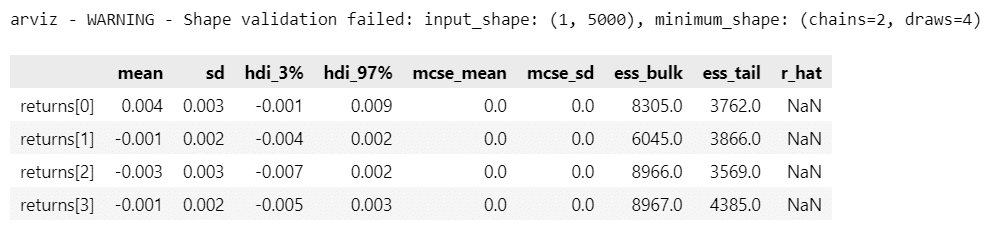
# returnsのトレースプロットの描画
pm.plot_trace(idata, var_names=['returns']);【実行結果】
右のプロットでは収束しているように見えます。
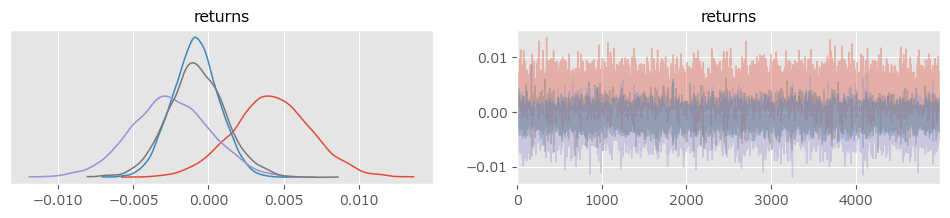
# returnsの事後分布プロットの描画 アップル,グーグル,テスラ,アマゾンの順
pm.plot_posterior(idata, var_names=['returns']);【実行結果】
新規コードの事後分布プロットの描画
日次リターンの$${\mu}$$の事後分布に関する新規コードを実行します。
新規コードからの変更はほぼありません。
# 日次リターンの事後分布の取得
mu_samples = idata.posterior.returns.data[0]
# 4銘柄の日次リターンの事後分布をプロット
plt.figure(figsize=(15, 6))
for i in range(4):
plt.hist(mu_samples[:, i], alpha=0.8-0.05*i, bins=30, histtype='stepfilled',
density=True, label=f'{stock_returns.columns[i]}')
plt.vlines(mu_samples.mean(axis=0), 0, 500, ls='--', lw=0.5)
plt.title('日次リターンの$\mu$の事後分布')
plt.legend()
plt.show()【実行結果】
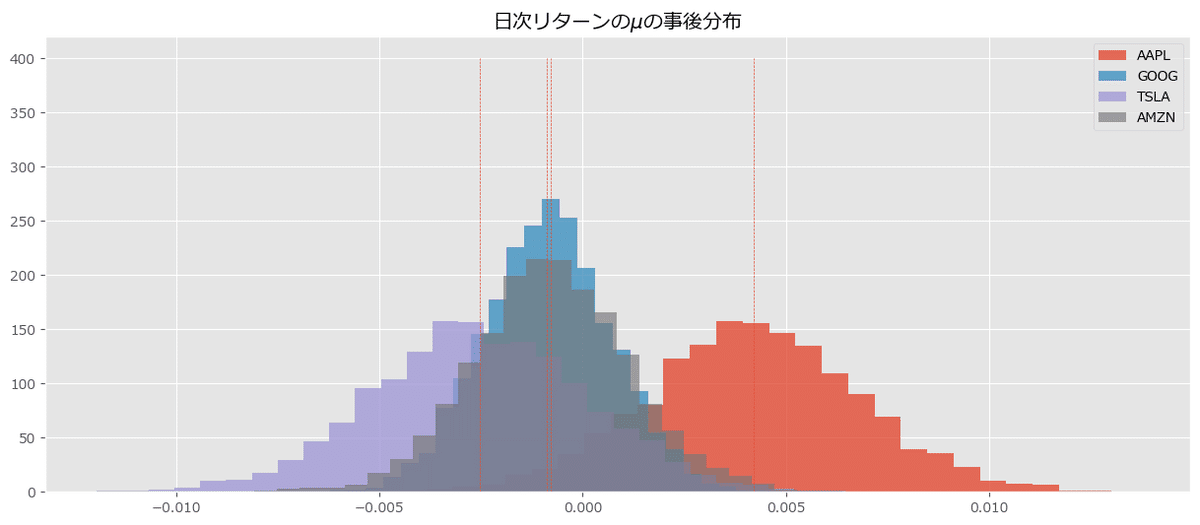
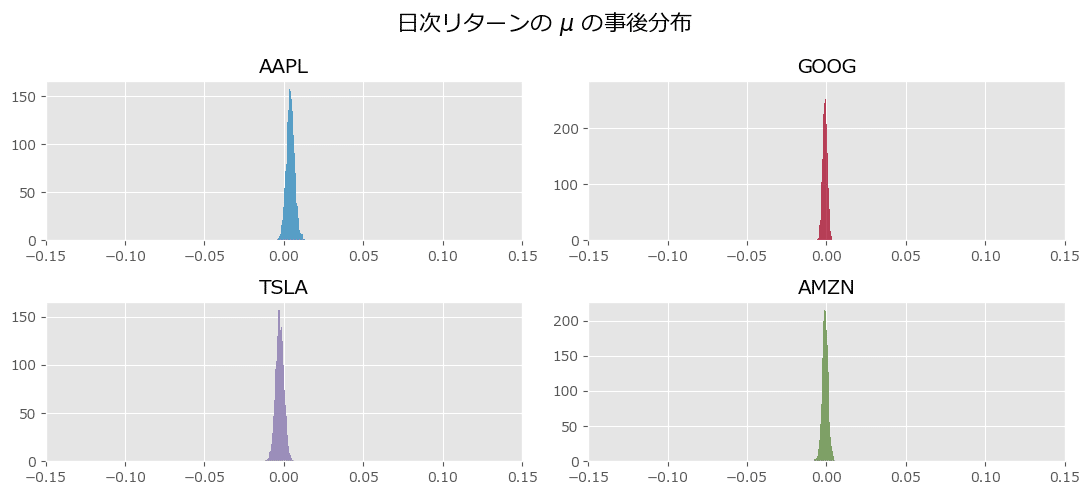
事前分布と同じ横軸の尺度で事後分布をプロットします。
新規コードから変更はほぼありません。
plt.figure(figsize=(11, 5))
for i, _stock in enumerate(stocks):
plt.subplot(2, 2, i+1)
plt.hist(mu_samples[:, i], alpha=0.8-0.05*i, bins=30, histtype='stepfilled',
density=True, color=colors[i], label=f'{stock_returns.columns[i]}')
plt.title(stock_returns.columns[i])
plt.xlim(-0.15, 0.15)
plt.suptitle(r'日次リターンの $\mu$ の事後分布', fontsize=16)
plt.tight_layout()
plt.show()【実行結果】
その2:付録
■ 対象コード
章末の「付録」「事前確率が0の場合」(テキスト218~220ページ)の「事前確率の実験」コードを取り扱います。

■ テキストの特徴
真値が$${0.35}$$であるパラメータ$${p}$$の事前分布を一様分布$${\text{Uniform}(0.5, 1)}$$にする場合、すなわち、分布の範囲に真値が入っていない事前分布を用いる場合について、実験しています。
■ 課題
GitHub には、付録の最新コードの掲載がありません。
そこで、この記事にて最新コード案の作成を試みます。
インポート
### インポート
import numpy as np
import pymc as pm
import matplotlib.pyplot as plt
plt.style.use('ggplot')
plt.rcParams['font.family'] = 'Meiryo'観測データの作成
テキストのコードからの変更はほぼありません。
### 観測データxの作成
# 真のpの値
p_accutual = 0.35
# ベルヌーイ分布 Ber(p)相当の二項分布から100個の乱数を得る
x = np.random.binomial(1, p_accutual, size=100)
# 乱数の先頭10個を表示
print(x[:10])【実行結果】
PyMCのモデル定義
とてもシンプルなモデルです。
### PyMCのモデルの定義
with pm.Model() as model:
# 事前分布
p = pm.Uniform('p', 0.5, 1)
# 尤度
obs = pm.Bernoulli('obs', p, observed=x)### モデルの表示
model【実行結果】

### モデルの可視化
pm.model_to_graphviz(model)【実行結果】
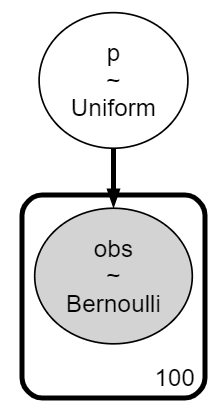
事後分布からのサンプリングと結果の可視化
### 事後分布からのサンプリング
with model:
idata = pm.sample(2500, tune=1000, chains=4, target_accept=0.9,
random_seed=123)【実行結果】

### 要約統計情報の表示
pm.summary(idata)【実行結果】

### トレースプロットの描画
pm.plot_trace(idata, figsize=(10, 3));【実行結果】
$${p}$$の推定値が「 $${0.5}$$ の壁を超えてもっと左側に行きたい!」と言っているように見えます。
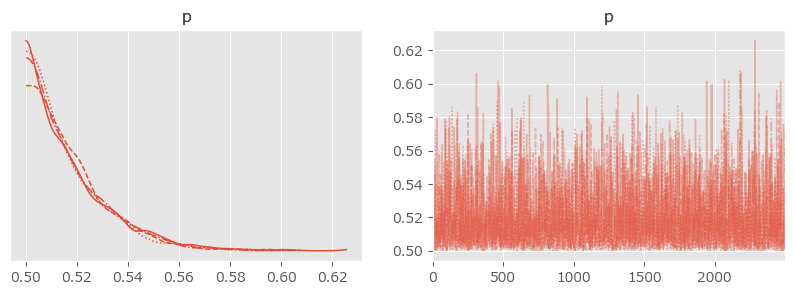
### 事後分布プロットの描画
pm.plot_posterior(idata, figsize=(10, 3));【実行結果】
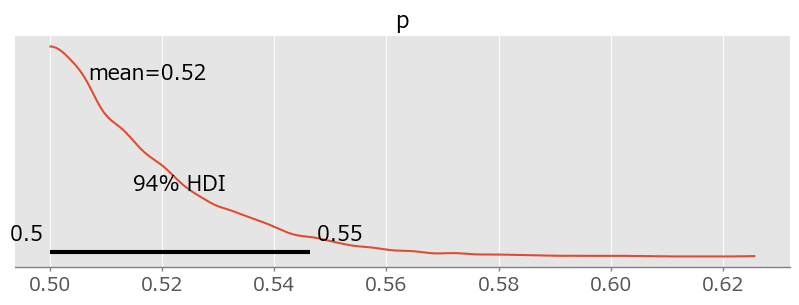
テキストの事後分布プロットの描画
1行目の推論データを取り出すコードを新しく作り、その他のコードはテキストを踏襲しています。
# 推論データの事後分布データからpを取り出して1次元化する
p_trace = idata.posterior.p.data.flatten()
# pの事後確率のヒストグラムをプロット
plt.figure(figsize=(12.5, 4))
plt.hist(p_trace, bins=30, histtype='stepfilled', density=True)
plt.xlabel('値')
plt.ylabel('密度')
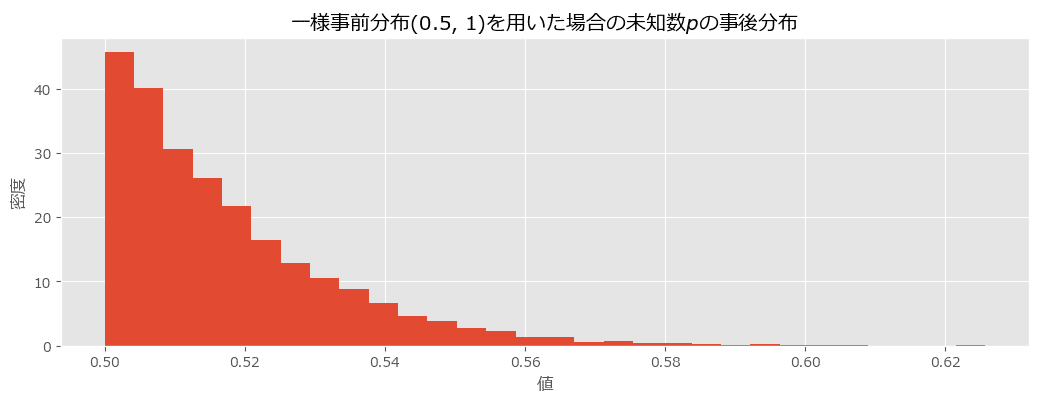
plt.title('一様事前分布(0.5, 1)を用いた場合の未知数$p$の事後分布')
plt.show()【実行結果】
事後分布が左に偏っており、事前分布が適切だったのかどうかの検討が必要そうです。

ここからは、個人的な実験です。
事前分布を一様分布$${\text{Uniform}(0, 1)}$$に変更してみます!
PyMCのモデル定義
### 事前分布を0~1の一様分布にしてみる
with pm.Model() as model:
# 事前分布
p = pm.Uniform('p', 0, 1)
# 尤度
obs = pm.Bernoulli('obs', p, observed=x)### モデルの表示
model【実行結果】

### モデルの可視化
pm.model_to_graphviz(model)【実行結果】
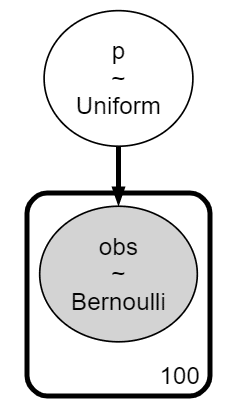
事後分布からのサンプリングと結果の可視化
### 事後分布からのサンプリング
with model:
idata = pm.sample(2500, tune=1000, chains=4, target_accept=0.9,
random_seed=123)【実行結果】

### 要約統計情報の表示
pm.summary(idata)【実行結果】
$${p}$$の平均が$${0.392}$$となり、真値$${0.35}$$に近づいています!
$${0.5}$$の壁を超えたのですね!
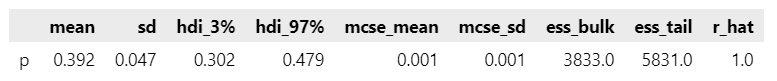
### トレースプロットの描画
pm.plot_trace(idata, figsize=(10, 3));【実行結果】
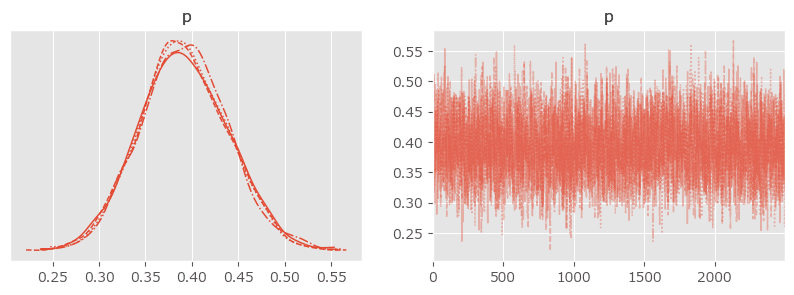
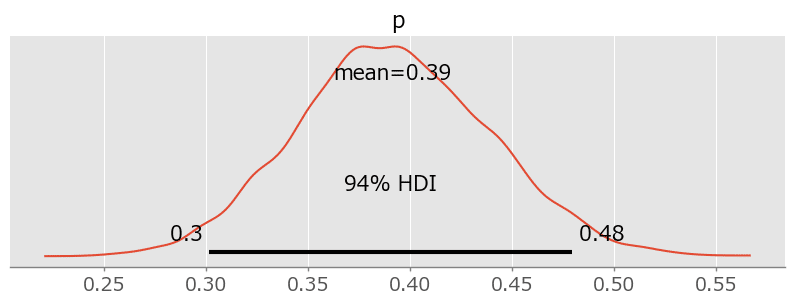
### 事後分布プロットの描画
pm.plot_posterior(idata, figsize=(10, 3));【実行結果】
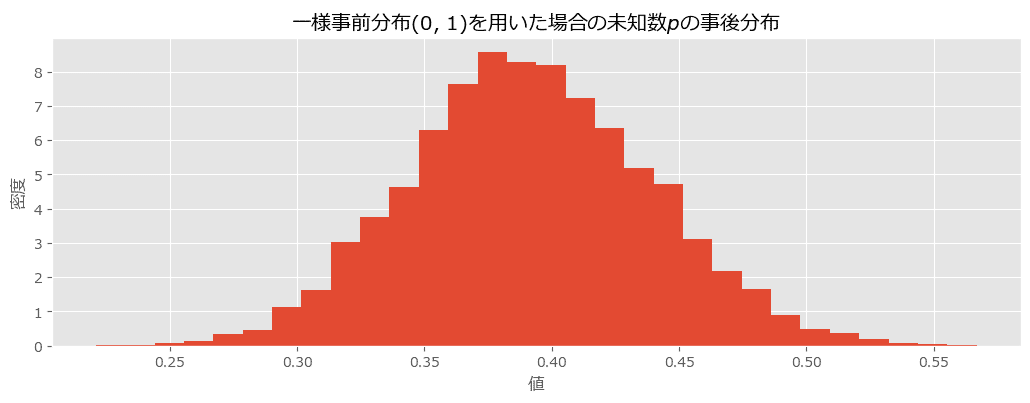
テキストの事後分布プロットの描画
# 推論データの事後分布データからpを取り出して1次元化する
p_trace = idata.posterior.p.data.flatten()
# pの事後確率のヒストグラムをプロット
plt.figure(figsize=(12.5, 4))
plt.hist(p_trace, bins=30, histtype='stepfilled', density=True)
plt.xlabel('値')
plt.ylabel('密度')
plt.title('一様事前分布(0, 1)を用いた場合の未知数$p$の事後分布')
plt.show()【実行結果】
事後分布が真値に近い$${0.39}$$あたりを中心にして1峰に分布しています。
事前分布のパラメータを変えて、めでたし、めでたし、の結果です。
第7章 ベイズ A/B テスト
■ 対象コード
「7.4.1 t検定の手順」(テキスト231~235ページ)の PyMC のモデリングに関連するコードを取り扱います。
■ テキストの特徴
第7章では、A/B テストに焦点をあてて、深い議論を行っています。
PyMC で BEST(ベイズ推定によるt検定)モデルを実装します。
サイト A とサイト B について、ユーザーのページ滞在時間に違いがあるかどうかを、このベイズ流のt検定で検討します。
■ 課題
GitHubには、第7章のコード(PyMC2から最新まで)の掲載が一切ありません。
出版社のサイトによると「権利の関係上、第7章のソースコードは公開しておりません」とのことです。
そこで、この記事にて最新コード案の作成を試みます。
対象範囲は、PyMC Ver.5 に変換の必要な部分に焦点を絞ります。

PyMCのモデル定義:テキスト232ページ後半から234ページ1行目まで
テキストでは、$${\mu_A, \mu_B}$$の事前分布である正規分布のパラメータに$${\tau}$$を利用しています。
【疑問点と対処内容】
テキストの$${\tau}$$の設定では、標準偏差×1000の「平方根」を取っています。
通常、$${\tau=1/\sigma^2}$$(二乗です)であり、なんだかモヤモヤします。
そこで、このコードでは、平方根に左右されること無く、標準偏差×1000を引数 sigma に設定しています。
もしかするとこの部分の影響で、テキストと異なる結果になる可能性があります。
### インポート
import pymc as pm### PyMCのモデル定義
## 初期値の設定
# 平均:データの平均
pooled_mean = np.r_[durarions_A, durarions_B].mean()
# 標準偏差:データの標準偏差の1000倍
pooled_std = np.r_[durarions_A, durarions_B].std()
sigma = pooled_std * 1000
## モデルの定義
with pm.Model() as model:
### パラメータ事前分布
# t分布の平均パラメータμ:正規分布
muA = pm.Normal('muA', mu=pooled_mean, sigma=sigma)
muB = pm.Normal('muB', mu=pooled_mean, sigma=sigma)
# t分布の標準偏差パラメータσ:一様分布
stdA = pm.Uniform('stdA', lower=pooled_std / 1000, upper=pooled_std * 1000)
stdB = pm.Uniform('stdB', lower=pooled_std / 1000, upper=pooled_std * 1000)
# t分布の自由度パラメータν:シフトした指数分布(平均=29、シフト=1)
nu = pm.Deterministic('nu', pm.Exponential('nu*', lam=1/29) + 1)
# 尤度:t分布
obsA = pm.StudentT('obsA', mu=muA, sigma=stdA, nu=nu, observed=durarions_A)
obsB = pm.StudentT('obsB', mu=muB, sigma=stdB, nu=nu, observed=durarions_B)
### モデルの表示
model【実行結果】
モデル定義の前に作成する durarions_A、 durarions_B は乱数シードが固定されていません。
この記事の数値と異なる値となる場合があることを、予めご了承ください。

### モデルの可視化
pm.model_to_graphviz(model)【実行結果】
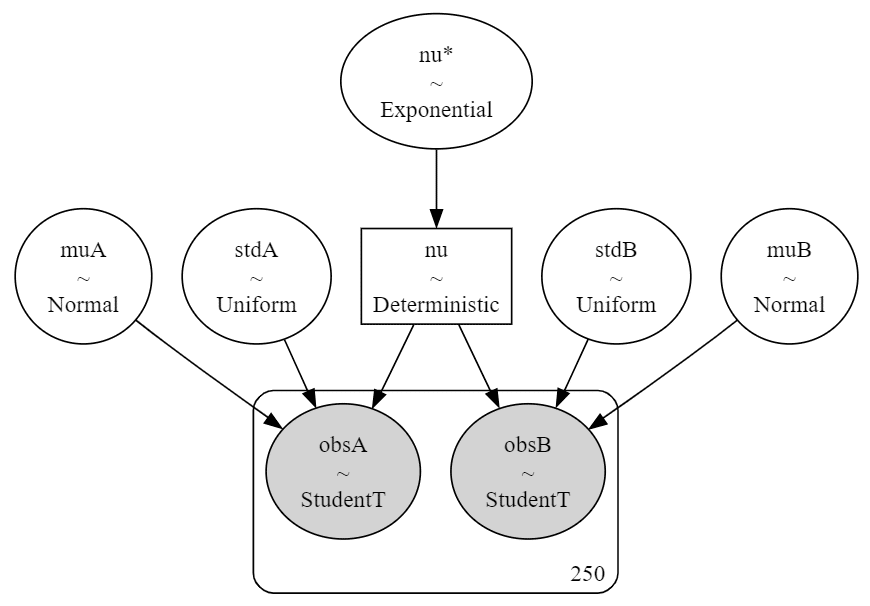
事後分布からのサンプリングと結果の可視化
### 事後分布からのサンプリング
with model:
idata = pm.sample(draws=6250, tune=2500, chains=4, random_seed=123,
target_accept=0.9)【実行結果】省略
### 事後分布からのサンプルの要約統計情報の表示
var_names=['muA', 'muB', 'stdA', 'stdB', 'nu']
pm.summary(idata, var_names=var_names)【実行結果】
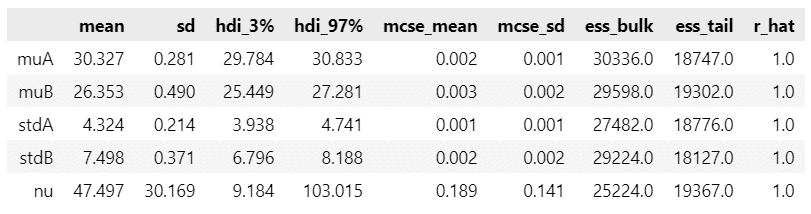
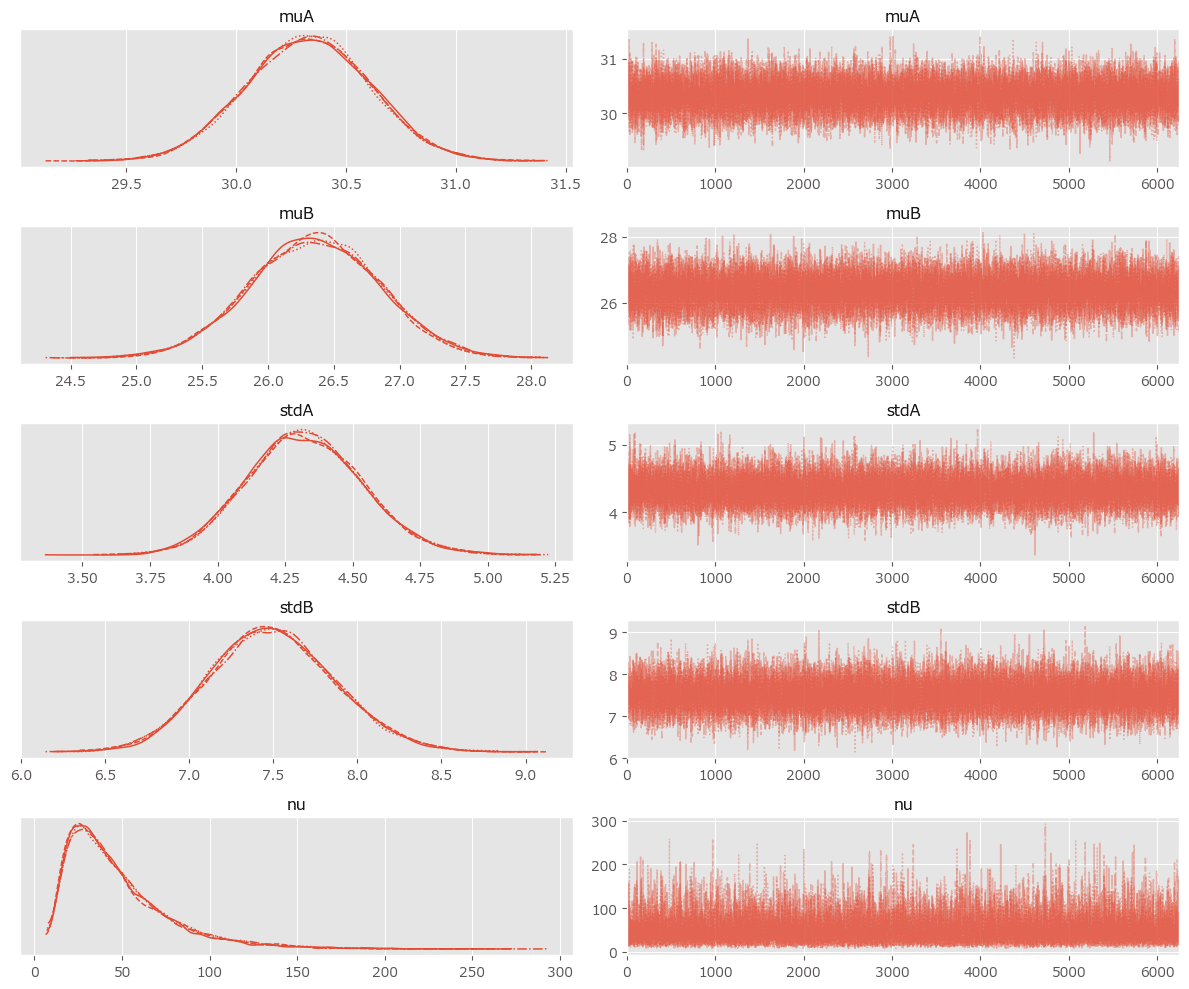
### トレースプロットの描画
pm.plot_trace(idata, var_names=var_names)
plt.tight_layout();【実行結果】
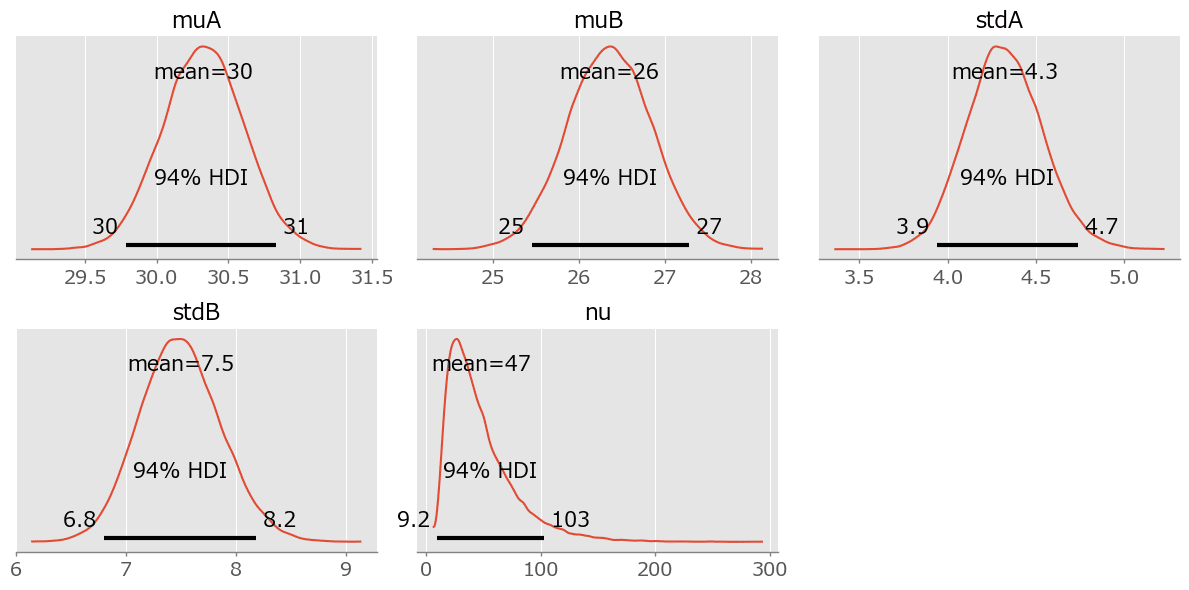
### 事後分布プロットの描画
pm.plot_posterior(idata, var_names=var_names, figsize=(12, 6))
plt.tight_layout();【実行結果】
テキストの事後分布プロットの描画
冒頭の事後分布からのサンプルデータ( idata )を捌く処理を変更しました。
その他はテキストのコードをほぼ踏襲しています。
# 事後分布からのサンプルデータをそれぞれの変数に1次元で格納
mu_A_trace = idata.posterior.muA.data.flatten()
mu_B_trace = idata.posterior.muB.data.flatten()
std_A_trace = idata.posterior.stdA.data.flatten()
std_B_trace = idata.posterior.stdB.data.flatten()
nu_trace = idata.posterior.nu.data.flatten()
# ヒストグラム描画関数の定義
def _hist(data, label, **kwargs):
return plt.hist(data, bins=40, histtype='stepfilled', alpha=0.95,
density=True, label=label, **kwargs)
# プロットの準備
plt.figure(figsize=(12, 8))
# μの事後分布のヒストグラムの描画
ax = plt.subplot(3, 1, 1)
_hist(mu_A_trace, 'A')
_hist(mu_B_trace, 'B')
plt.xlabel('値')
plt.ylabel('密度')
plt.title(r'$\mu$の事後分布')
plt.legend()
# σの事後分布のヒストグラムの描画
ax = plt.subplot(3, 1, 2)
_hist(std_A_trace, 'A')
_hist(std_B_trace, 'B')
plt.xlabel('値')
plt.ylabel('密度')
plt.title(r'$\sigma$の事後分布')
plt.legend()
# νの事後分布のヒストグラムの描画
ax = plt.subplot(3, 1, 3)
_hist(nu_trace, '', color='#7A68A6')
plt.xlabel('値')
plt.ylabel('密度')
plt.title(r'$\nu$の事後分布')
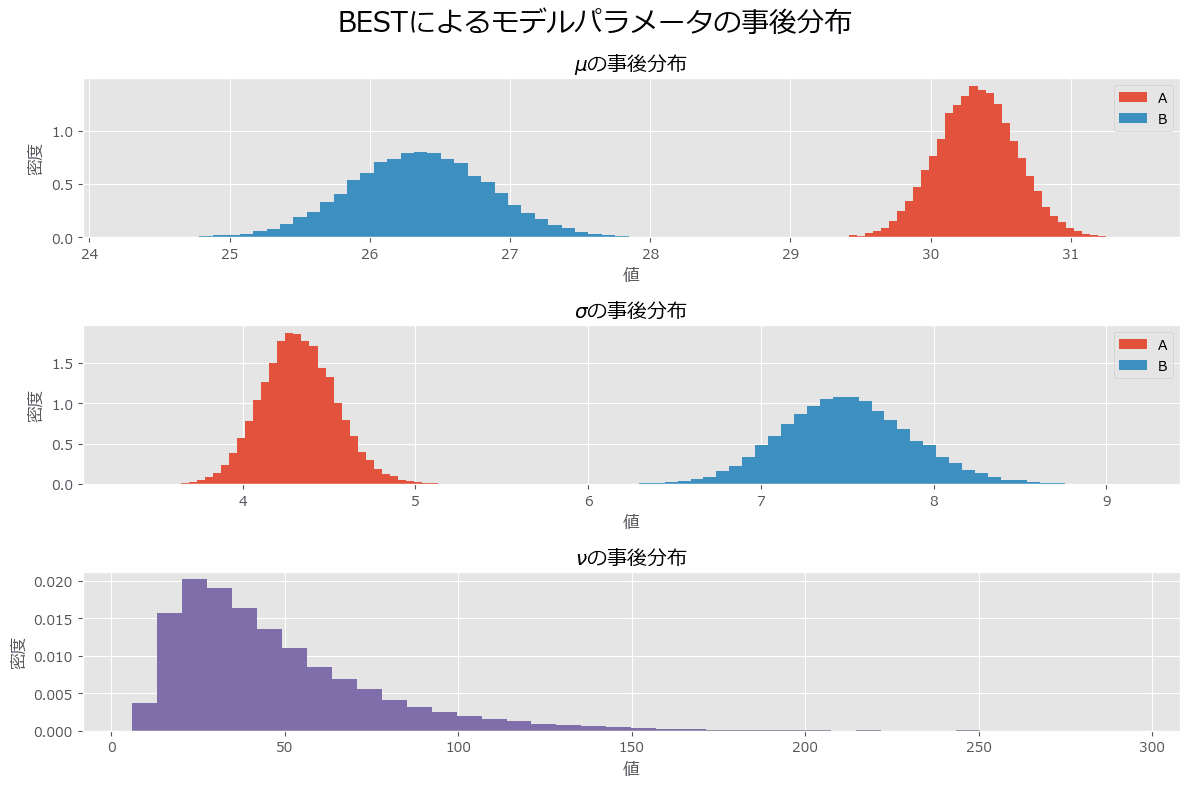
plt.suptitle('BESTによるモデルパラメータの事後分布', fontsize=20)
plt.tight_layout()
plt.show()【実行結果】
サイト B と比べて、サイト A のほうが滞在時間が長く、散らばりも少ないことが分かりました。
以上でテキストのコード検討はおしまいです。
ご清聴ありがとうございました。

結び
テキストの多様な例題の中で、個人的には、第5章のダークマターの位置を推論する例題が面白かったです。
ベイズ推論が Kaggle コンテストで機械学習に打ち勝ったのです。
ベイズと宇宙のWロマンを感じました✨
このようにテキストを円滑に楽しく学べたのは、GitHub に PyMC Ver.5 で動く新規コードが掲示されていたおかげです。
開発スピードが速い PyMC Ver.5 に新規コードが通用しているのが凄いです!
私が学び始めた2023年7月の時点の PyMC は Ver. 5.5.0 、9月現在は Ver. 5.8.2です(いずれも Anaconda 環境用)。
自分がコードの変化に追随できるのか、ちょっと心配です(汗)
はやく Ver.5 対応の PyMC テキストが出版されないかな、、、
話は変わって、PyMC の NUTS サンプラーに「numpyro」を用いたところ、サンプリング処理がものすごく速くなりました!
このテキストにはサンプリング処理に 30 分以上かかるケースがあり、numpyro のおかげで、待ち時間が短縮化され、スピーディーにコードを学ぶことができました。

【 numpyro のご案内】
■ インストール:pip でインストールしました。
※ なぜだか conda でインストールできなかったです。
### numpyro のインストール
pip install numpyro■使用: pm.sample の引数に「nuts_sampler='numpyro'」を指定します。
with model:
idata = pm.sample(10000, ・・・, nuts_sampler='numpyro')ぜひ、高速 MCMC の世界をご堪能ください。

おわり
ブログの紹介
note で3つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
2.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learn と PyTorch の教科書です。
よかったらぜひ、お試しくださいませ。
3.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Python のコラムを不定期に綴っています。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
最後までお読みいただきまして、ありがとうございました。
