9-1-1 適合度検定の基本～カテゴリ集計とカイ二乗検定統計量と電卓テクが交錯する時

ネイピア DS

2023年9月20日 11:14

統計的仮説検定のトピック「適合度の検定」の章に進みます。
観測度数と期待度数から始まる適合度の検定の旅をお楽しみくださいませ。

公式問題集の準備

「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください！
「知る」「実践する」の章で、のんびり統計をお楽しみください！

問題を解いて、知る・実践する

今回の記事の構成

この記事は、通常の記事構成と違う章立てにいたします。
「問題を解く」「知る」「実践する」を１つの章にまとめます。
適合度検定の一連の流れを、手作業・EXCEL・Pythonで実践いたします。

📘公式問題集のカテゴリ

カイ二乗検定の分野　～適合度検定の分野
問1 適合度検定の基本（くじ引きの当りの確率）

試験実施年月
調査中

📕公式テキスト：6.2 適合度の検定（203ページ～）

問題

公式問題集をご参照ください。

解き方

題意
与えられた条件に基づき、適合度の検定に関わる$${\chi^2}$$分布の「自由度」、「検定統計量」、「帰無仮説を棄却できるかどうか」を解答します。

【条件】
・観測度数は、1等：5、2等：12、はずれ：33（標本サイズ50）
・仮定する確率は、1等：20%、2等：30%、はずれ：50%
　（くじは大量に用意されている）
・帰無仮説は「観測データは仮定する確率と一致する」
・有意水準$${5\%}$$で適合度検定を行う

公式問題集の記述を改変

読み解き

条件から統計的仮説検定の主題を読み解きます。

条件より「適合度の検定」を行います。
適合度の検定は「片側検定（上側）」です。
仮定した確率に基づいて期待度数を計算します。
観測度数と期待度数を用いて、検定統計量$${\chi^2}$$を計算します。
検定統計量$${\chi^2}$$が従う$${\chi^2}$$分布の自由度を計算します。
$${\chi^2}$$分布のパーセント点表より、有意水準$${5\%}$$のパーセント点を取得して、帰無仮説を棄却できるかどうか結論づけます。

この問題の統計的仮説検定の概要を図示します。

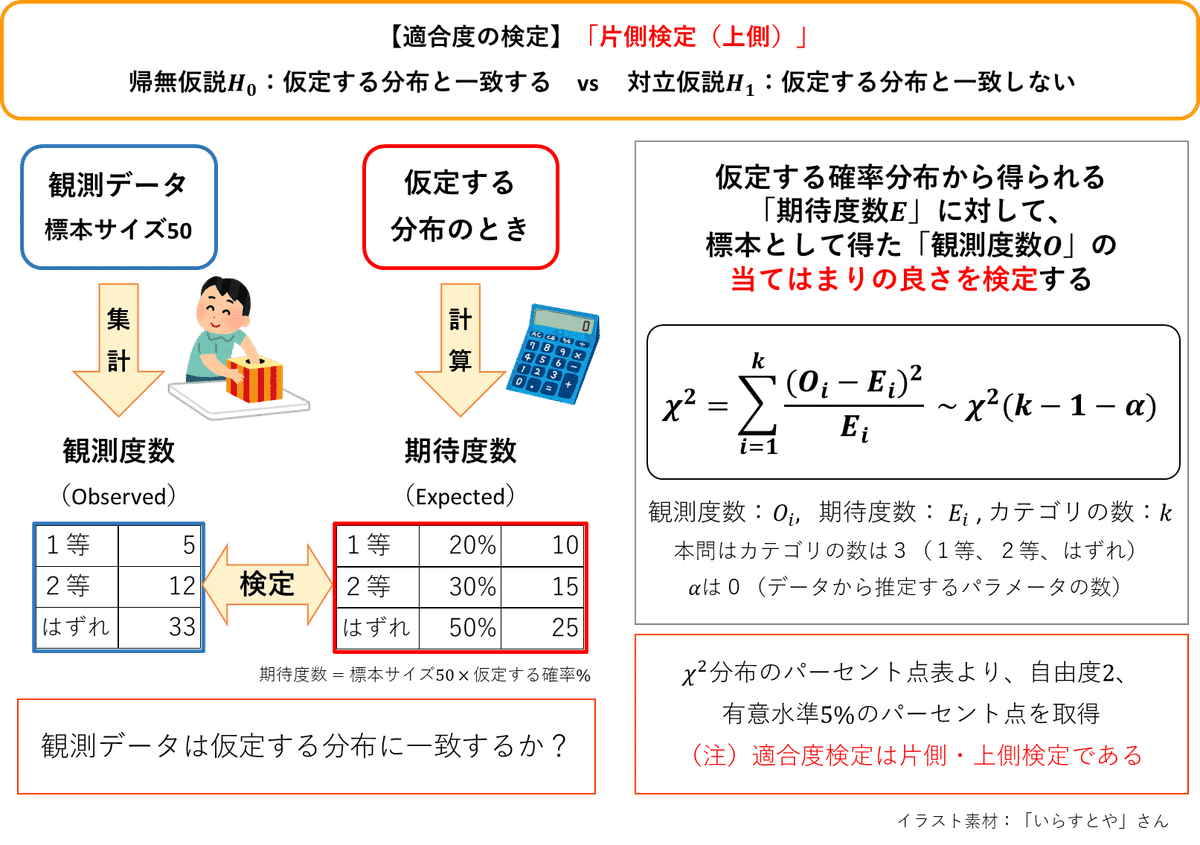
統計的仮説検定の手段

今回は、①手計算、②EXCEL、③Python の３つの手段で検定を実施いたします。

手計算で検定

ステップ１：期待度数を計算する

期待度数は、理論的な確率や想定する確率といった「仮定する分布」の下でカウントされる度数です。

本問の仮定する分布（確率）は次のとおりです。

50人（標本サイズ）について、仮定する分布（確率）を用いて、期待度数を計算します。
$${50 \times 各等の確率}$$で求めます。
・１等：$${50 \times 20\% = 10}$$
・２等：$${50 \times 30\% = 15}$$
・はずれ：$${50 \times 50\% = 25}$$

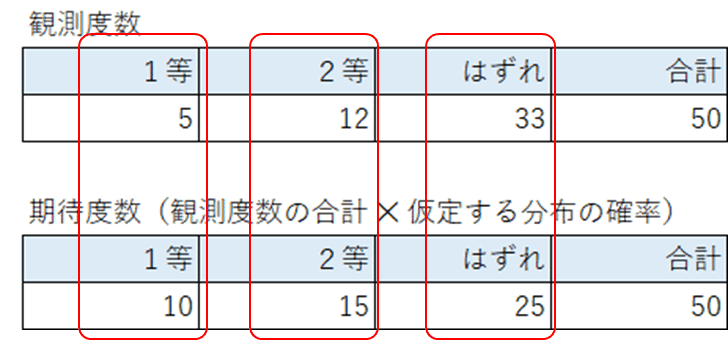
期待度数を表にしましょう。

次の計算で観測度数と期待度数を用いるので、両方の度数をまとめて掲載しましょう。

期待度数と比べて、観測度数の当たり目（実際に１等・２等が出た数）はかなり少ないように思えます。
巷で言われている当たりの確率（仮定する分布）を疑ってしまいますね。。。

ステップ２：検定統計量$${\boldsymbol{\chi^2}}$$を計算する

最初の山場です！
カテゴリ（分類）ごとに「観測度数と期待度数の差の２乗」を「期待度数で割り」、全カテゴリを合計します。

本問のカテゴリは「１等」「２等」「はずれ」の３つです。
検定統計量$${\chi^2}$$は次の計算式を用いて計算します。

先程まとめた観測度数と期待度数の値を当てはめて、検定統計量$${\chi^2}$$を計算しましょう。

検定統計量の計算で得られた$${\chi^2}$$値は$${5.66}$$です。

解答選択肢（イ）の$${\chi^2}$$値は$${5.66}$$です。

【試験ワンポイント】

適合度検定はカテゴリの数が増えるほどに計算量が増大するため、統計検定©の試験のときには電卓の速度と正確性が問われる「大計算問題」になります。
簡単な攻略法を記載します。

まず、計算式を組み立ててメモ用紙に記載します。

メモ用紙を手がかりにして、次のように電卓をひたすら打鍵します。

5-10×=÷10[M+] 12-15×=÷15[M+] 33-25×=÷25[M+] [RM]

電卓画面には$${\chi^2}$$値$${5.66}$$が表示されているはずです。

二乗は「×=」、加算・減算の累積はメモリー機能の「M+」「M-」を活用します。
お手持ちの電卓の操作方法をご確認の上、My電卓術を編み出してください。

ステップ３：検定統計量$${\boldsymbol{\chi^2}}$$が従う$${\boldsymbol{\chi^2}}$$分布の自由度

観測度数が１変数の場合、検定統計量$${\chi^2}$$は自由度$${k-1-\alpha}$$の$${\chi^2}$$分布に従います。
$${k}$$はカテゴリの数です。
$${\alpha}$$は観測データから推定する分布のパラメータの数（補足参照）です。
本問で取り扱う観測度数は「当たりの種類」の１変数であり、カテゴリの数は３（１等、２等、はずれの３つ）、データから推定するパラメータの数は０ですので、自由度は$${k-1-\alpha=3-1-0=2}$$です。

解答選択肢（ア）の自由度は$${2}$$です。

【補足】データから推定するパラメータの数

大半の統計検定２級の問題では、「データから推定するパラメータの数」を意識する必要はありません。
自由度は「カテゴリの数－１」で求めます。

ただし、仮定する分布にポアソン分布を想定する問題では注意が必要です。
観測データからポアソン分布の平均パラメータ$${\lambda}$$の推定値$${\hat{\lambda}}$$を求めて、期待度数を計算するケースがあります。
この場合、観測データから分布のパラメータを１つ推定しているので、$${\chi^2}$$分布の自由度は$${k-1\boldsymbol{-1}}$$のように、推定パラメータ個数を最後に差し引きします。

ステップ４：検定統計量$${\boldsymbol{\chi^2}}$$が従う$${\boldsymbol{\chi^2}}$$分布の上側パーセント点

続いて上側パーセント点を取得して棄却域を確認します。
ここで重要なお知らせ。

【重要ポイント】
・適合度検定は片側・上側検定です。

適合度検定は片側・上側検定ですので、有意水準$${5\%}$$の棄却域を求める際には、自由度$${2}$$の$${\chi^2}$$分布のパーセント点表より上側確率$${5\%}$$点を取得します。

自由度$${2}$$の上側確率$${5\%}$$点は$${5.99}$$です。

$${\chi^2}$$分布の確率密度関数をグラフで確認しましょう。

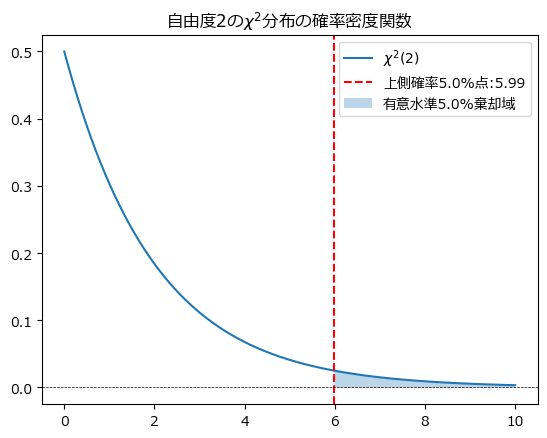
ステップ５：結論を出す

$${\chi^2}$$値$${=5.66}$$と上側確率$${5\%}$$点$${=5.99}$$を比べます。
$${\chi^2}$$値は上側確率$${5\%}$$点より小さいため、棄却域から外れています。
よって、帰無仮説は棄却されません。

解答選択肢（ウ）は棄却「できない」です。

つまり、観測データが巷で言われている当たりの確率「１等20%、２等30%」と異なる、とは言えないのです。
実際に起きたことを記録した観測度数を見る限りでは、１等が20%も出るとは思えないのですが、適合度検定はこの思いを受け止めてくれないようです。

最後にグラフで棄却域と$${\chi^2}$$値の関係を確認しましょう。

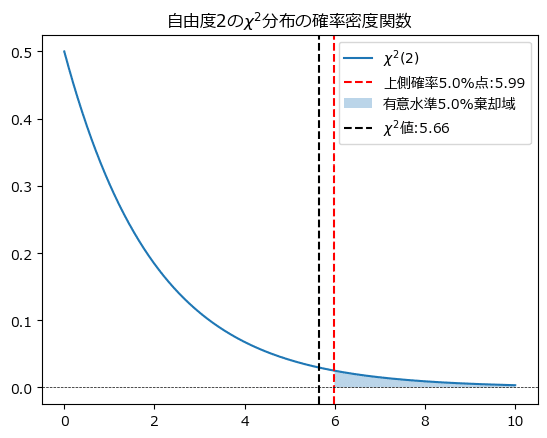
確かに$${\chi^2}$$値は棄却域から外れています。

手計算は以上となります。

EXCELで検定

計算シートを用いて適合度検定を行います。

計算シートの全体像
左側の表には、観測度数と仮定する分布（確率）を登録します。
期待度数を計算して、観測度数・期待度数の両方を整えます。
右側の入力パラメータは「有意水準」です。

観測度数・期待度数・有意水準より、$${\chi^2}$$値、上側確率％点、$${p}$$値を求めて、判定します。

適合度検定の実行

上記の計算シートには既に必要なデータ、パラメータを設定済みです。
計算値によると、自由度は$${2}$$、$${\chi^2}$$値は$${5.66}$$、上側確率$${5\%}$$点は$${5.991}$$です。
$${\chi^2}$$値が上側確率5%点よりも小さいので、帰無仮説は棄却できません。

解答選択肢は（ア）$${2}$$、（イ）$${5.66}$$、（ウ）できない、です。

EXCELの関数

EXCELの CHISQ.TEST 関数を用いて、適合度検定の$${p}$$値を算出できます。
引数は、CHISQ.TEST ( 観測度数のデータ範囲, 期待度数のデータ範囲 ) です。
シンプルなのでぜひ使ってみてください！

EXCELは以上となります。

EXCELサンプルファイルのダウンロード
こちらのリンクからEXCELサンプルファイルをダウンロードできます。

Pythonで検定

scipy.stats の chisquare を用いて適合度検定を実行します。

①インポート

### インポート
import numpy as np
import pandas as pd
from scipy import stats
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Meiryo'

②データとパラメータの設定
問題で与えられた「観測度数」、「仮定する確率」、「有意水準」を設定します。
この３つの情報から、期待度数、自由度、上側確率$${5\%}$$点を算出します。
$${\chi^2}$$分布の上側確率$${5\%}$$点の取得には、scipy.stats の chi2.isf を利用しました。

### データとパラメータの設定

## 設定
# 観測度数 : １等,２等, はずれの順
observed_freq = np.array([5, 12, 33])
# 仮定する確率
expected_prob = np.array([0.2, 0.3, 0.5])
# 有意水準
alpha = 0.05

## 検定に利用する値の計算（設定）
# 期待度数
excepted_freq = expected_prob * observed_freq.sum()
# 自由度
df = observed_freq.shape[0] - 1
# 有効水準のカイ二乗分布の上側パーセント点
critical_value = stats.chi2.isf(alpha, df)

## 観測度数と期待度数の表示
display(pd.DataFrame(data={'観測度数': observed_freq,
                           '期待度数': excepted_freq},
                     index=['1等', '2等', 'はずれ']).T)

③適合度検定の実施
scipy.stats の chisquare を用いて適合度検定を行います。
引数は、chisquare ( 観測度数データ, 期待度数データ ) です。
戻り値は、$${\chi^2}$$値と$${p}$$値です。

### 適合度検定の実施
chi2_value, p_value = stats.chisquare(observed_freq, excepted_freq)
print(f'chi2_value:{chi2_value:.3f}, p_value:{p_value:.3f}')

出力イメージ

④結論の表示
有意水準と$${p}$$値を比較して、帰無仮説を棄却できるかどうかを判定します。

### 結論の表示
if p_value < alpha:  # p値が有意水準より小さい場合：棄却できる
    result = ('棄却される', '言える')
else:                # p値が有意水準以上の場合：棄却できない
    result = ('棄却されない', '言えない')
print(f'結論\n有意水準{alpha:.1%}で帰無仮説は{result[0]}\n'
      f'対立仮説「観測データは仮定する確率分布に一致しない」と{result[1]}')

### 検定統計量の表示
print('\n検定統計量')
print(f'自由度{df}のカイ二乗分布の上側{alpha:.1%}点:{critical_value:.3f}, '
      f'カイ二乗値:{chi2_value:.3f}')
print(f'有意水準{alpha:.3f}, p値:{p_value:.3f}')

解答選択肢は（ア）$${2}$$、（イ）$${5.66}$$、（ウ）できない、です。

Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。

以上で終了です。
お疲れ様でした。

解答

④ です。

難易度　やさしい

・知識：適合度の検定、$${\chi^2}$$分布のパーセント点表
・計算力：数式組み立て（低）、電卓（中）
・時間目安：2分

おわりに

この記事から「適合度の検定」のテーマに進みました。
$${\chi^2}$$を用いた検定は計算パターンさえ押さえれば、統計検定©試験の得点源になります。
ぜひ、「観測度数と期待度数」・「カテゴリ」・「自由度」・「検定統計量$${\chi^2}$$の公式」・「片側・上側検定」「$${\chi^2}$$分布のパーセント点表」を体得してくださいね。

最後までお読みいただきまして、ありがとうございました。

のんびり統計シリーズの記事

次の記事

前の記事