
「数値シミュレーションで読み解く統計のしくみ」をPythonで写経 ~ 第7章7.3「回帰分析における仮定と注意点」
第7章「回帰分析とシミュレーション」
書籍の著者 小杉考司 先生、紀ノ定保礼 先生、清水裕士 先生
この記事は、テキスト「数値シミュレーションで読み解く統計のしくみ」第7章「回帰分析とシミュレーション」の7.3節「回帰分析における仮定と注意点」の Python写経活動 を取り扱います。
第7章は回帰分析を掘り下げます。
今回は回帰分析の2つの仮定のシミュレーションと対処策を実践します。

R の基本的なプログラム記法はざっくり Python の記法と近いです。
コードの文字の細部をなぞって、R と Python の両方に接近してみましょう!
ではテキストを開いてシミュレーションの旅に出発です🚀
はじめに
テキスト「数値シミュレーションで読み解く統計のしくみ」のご紹介
このシリーズは書籍「数値シミュレーションで読み解く統計のしくみ〜Rでためしてわかる心理統計」(技術評論社、「テキスト」と呼びます)の Python写経です。
テキストは、2023年9月に発売され、副題「Rでためしてわかる心理統計」のとおり、統計処理に定評のある R の具体的なコードを用いて、心理統計の理解に役立つ数値シミュレーションを実践する素晴らしい書籍です。
引用表記
この記事は、出典に記載の書籍に掲載された文章及びコードを引用し、適宜、掲載文章とコードを改変して書いています。
【出典】
「数値シミュレーションで読み解く統計のしくみ〜Rでためしてわかる心理統計」初版第1刷、著者 小杉考司・紀ノ定保礼・清水裕士、技術評論社
記事中のイラストは、「かわいいフリー素材集いらすとや」さんのイラストをお借りしています。
ありがとうございます!
7.3 回帰分析における仮定と注意点
この章では以下の2つの仮定を取り扱います
① 残差の等分散性
② 説明変数同士が無相関

この記事は Jupyter Notebook 形式(拡張子 .ipynb)でPythonコードを書きます。
概ね確率分布の特性値算出には scipy.stats を用い、乱数生成には numpy.random.generator を用いるようにしています。
主に利用するライブラリをインポートします。
### インポート
# 数値計算
import numpy as np
# データフレーム
import pandas as pd
# 確率・統計
import scipy.stats as stats
import statsmodels.formula.api as smf # 回帰分析等の統計処理
from statsmodels.stats import sandwich_covariance # サンドイッチ共分散
from statsmodels.stats.outliers_influence import variance_inflation_factor # VIF
import pingouin as pg # 統計便利ツール
import lmdiag # 残差プロット
# 主成分分析
from sklearn.decomposition import PCA
# グラフ描画
from graphviz import Digraph
# 描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'
7.3.1 残差についての仮定
テキストによると「回帰分析は残差の分散が説明変数の値に対して一定と仮定され、残差$${e_i}$$は平均0、残差の分散$${\sigma^2}$$の正規分布に従う」としています。
テキストのシミュレーションで用いる不均一分散を表すモデル数式をお借りします。
説明変数$${x_i}$$の大きさに応じて、影響力$${\tau}$$で残差が大きくなるモデルです。
$$
\begin{array}{ll}
均一の場合 & e_i \sim \text{Normal}\ (0,\ \sigma) \\
不均一の場合 & e_i \sim \text{Normal}\ (0,\ e^{x_i\tau}) \\
\end{array}
$$
テキスト図7.5の不均一分散の残差の散らばりの図を描画します。
影響力$${\tau=1.5}$$です。
### 273ページ 図7.5 残差分散が一様でないときの説明変数と目的変数の散布図
## 設定と準備
n = 500 # サンプルサイズ
beta0 = 0 # 切片
beta1 = 0.5 # 傾き
tau = 1.5 # 残差の大きさの影響力
## データの作成
rng = np.random.default_rng(seed=123)
# x: 範囲[-1, 1)の連続一様分布乱数
x = rng.uniform(size=n, low=-1, high=1)
# 残差e: 平均0, 標準偏差exp(xτ)の正規分布乱数
e_hetero = rng.normal(size=n, loc=0, scale=np.exp(x * tau))
# y: 切片beta0 + 傾きbeta1 * x + 残差
y = beta0 + beta1 * x + e_hetero
## 描画
plt.figure(figsize=(6, 3))
plt.scatter(x, y, s=60, ec='white', alpha=0.7)
plt.xlabel('x')
plt.ylabel('y')
plt.title('残差分散が一様でないときの\n説明変数 $x$ と目的変数 $y$ の散布図');【実行結果】
説明変数$${x}$$の値が大きくなるほど目的変数$${y}$$のバラツキが大きくなっている様子が分かりました。


■ 不均一分散の係数の可視化
均一分散と不均一分散を比較して、不均一分散の特徴を確認します。
まず均一分散と不均一分散のデータ生成と係数の推定値・標準誤差を算出する関数を定義します。
### 273ページ 均一分散と不均一分散の回帰係数・標準誤差を算出する関数
def lm_hetero(n, beta0, beta1, sigma, tau):
# 説明変数の生成
x = rng.uniform(size=n, low=-1, high=1)
# 均一な残差の生成
e_homo = rng.normal(size=n, loc=0, scale=sigma)
# 不均一な残差の生成
e_hetero = rng.normal(size=n, loc=0, scale=np.exp(x * tau))
# 均一分散の目的変数(理論値)
y_homo = beta0 + beta1 * x + e_homo
# 不均一分散の目的変数(理論値)
y_hetero = beta0 + beta1 * x + e_hetero
# おのおの分析
model_homo = smf.ols('y_homo ~ x', data=dict(x=x, y_homo=y_homo)).fit()
model_hetero = smf.ols('y_hetero ~ x', data=dict(x=x, y_hetero=y_hetero)
).fit()
# 結果の格納
results = np.array([
model_homo.params.iloc[0], # 均一分散のbeta0
model_homo.params.iloc[1], # 均一分散のbeta1
model_homo.bse.iloc[0], # 均一分散のbeta0のSE
model_homo.bse.iloc[1], # 均一分散のbeta1のSE
model_hetero.params.iloc[0], # 不均一分散のbeta0
model_hetero.params.iloc[1], # 不均一分散のbeta1
model_hetero.bse.iloc[0], # 不均一分散のbeta0のSE
model_hetero.bse.iloc[1], # 不均一分散のbeta1のSE
])
return results続いてデータ生成・係数の推定を実行します。
シミュレーション回数は 1000 回です。
パラメータは以下のとおりです。
・サンプルサイズ$${n=500}$$
・切片$${\beta_0=1}$$、傾き$${\beta_1=0.5}$$
・残差標準偏差$${\sigma=1}$$
・残差の大きさの影響力$${\tau=1.5}$$
### 274ページ シミュレーションの実行
## 設定と準備
iter = 1000 # シミュレーション回数
n = 500 # サンプルサイズ
beta0 = 1 # 切片
beta1 = 0.5 # 傾き
sigma = 1 # 標準偏差
tau = 1.5 # 残差の大きさの影響力
## 結果を格納するオブジェクト
results = np.zeros((iter, 8))
## シミュレーション
rng = np.random.default_rng(seed=123)
for i in range(iter):
results[i, :] = lm_hetero(n, beta0, beta1, sigma, tau)
## 結果(データフレームに)
df = pd.DataFrame(
results,
columns=['beta0_homo', 'beta1_homo', 'se0_homo', 'se1_homo',
'beta0_hetero', 'beta1_hetero', 'se0_hetero', 'se1_hetero'])
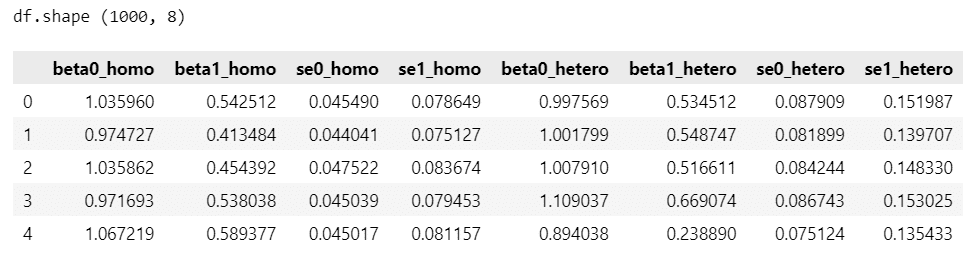
print('df.shape', df.shape)
display(df.head())【実行結果】
homoは均一分散、heteroは不均一分散です。
ここからは不均一分散の係数の可視化です。
まずは切片から。
### 275ページ 分散均一と分散不均一の切片の推定値の分布 図7.6
# 描画領域の設定
fig, ax = plt.subplots(figsize=(6, 3))
# 分散均一の切片の推定値のカーネル密度推定の描画
sns.kdeplot(data=df, x='beta0_homo', label='分散均一', ax=ax)
# 分散不均一の切片の推定値のカーネル密度推定の描画
sns.kdeplot(data=df, x='beta0_hetero', color='tab:red', ls='--',
label='分散不均一', ax = ax)
# 切片の理論値1の垂直線の描画
ax.axvline(1, color='black')
# y軸範囲、x軸ラベル、タイトルの設定
ax.set(ylim=(-0.3, 10), xlabel='beta0', title='density plot of beta0')
# 凡例表示
ax.legend();【実行結果】

続いて傾きです。
### 275ページ 分散均一と分散不均一の傾きの推定値の分布 276ページ図7.7
# 描画領域の設定
fig, ax = plt.subplots(figsize=(6, 3))
# 分散均一の傾きの推定値のカーネル密度推定の描画
sns.kdeplot(data=df, x='beta1_homo', label='分散均一', ax=ax)
# 分散不均一の傾きの推定値のカーネル密度推定の描画
sns.kdeplot(data=df, x='beta1_hetero', color='tab:red', ls='--',
label='分散不均一', ax = ax)
# 傾きの理論値0.5の垂直線の描画
ax.axvline(0.5, color='black')
# y軸範囲、x軸ラベル、タイトルの設定
ax.set(ylim=(-0.3, 8), xlabel='beta1', title='density plot of beta1')
# 凡例表示
ax.legend();【実行結果】

切片も傾きも、不均一分散のほうがバラツキが大きくなっています。
テキストによると「不均一分散の標準誤差は大きくなっていることが確認できます」です。

■ 不均一分散の問題点
不均一分散の問題点についてテキストは、回帰分析結果の係数の標準誤差は均一分散を前提としているため、「不均一分散の係数の散らばり」を過小評価している、と指摘しています。
シミュレーションデータの不均一分散について、①推定した傾きから算出した標準偏差と、②回帰分析による傾きの標準誤差の平均値を比較してみます。
①推定した傾きから算出した標準偏差
### 276ページ 不均一分散データの係数の標準偏差
df['beta1_hetero'].std(ddof=1)【実行結果】

②回帰分析による傾きの標準誤差の平均値
### 276ページ 不均一分散データを回帰分析して推定した標準誤差の推定値
df['se1_hetero'].mean()【実行結果】
確かに回帰分析結果の係数の標準誤差は過小になっています。


■ 残差分析によって確認できる不均一分散
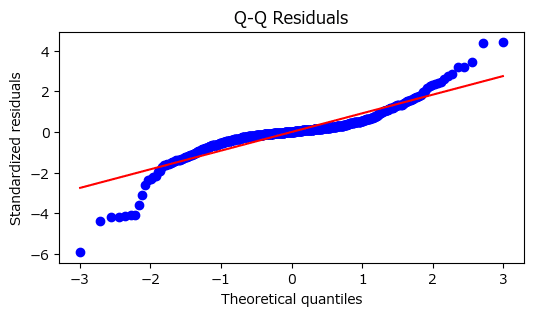
テキストは、回帰分析実行後に残差を確認することが重要と指摘し、「不均一分散の例を確認するとQ-Qプロットの横軸の両端において直線から外れる値が多く存在」することを把握でき「モデルの仮定が満たされていないことがわかります」としています。
Pythonの3つのライブラリでQ-Qプロットを描画します!
① scipy.stats の probplot
### 277ページ Q-Qプロットの描画 図7.8
## 設定と準備
n = 500
beta0 = 1
beta1 = 0.5
gamma = 1.5
## データの作成
rng = np.random.default_rng(seed=123)
# 説明変数x
x = rng.uniform(size=n, low=-1, high=1)
# 分散不均一の残差項
e_hetero = rng.normal(size=n, loc=0, scale=np.exp(x * gamma))
# 目的変数y
y = beta0 + beta1 * x + e_hetero
# 回帰分析の実行 statsmodels
result = smf.ols(formula='y ~ x', data=dict(x=x, y=y)).fit()
## 描画 stats.modelsのprobplotで描画
# 描画領域の設定
plt.figure(figsize=(6, 3))
# Q-Qプロットの描画: 回帰分析結果resultから.residで残差を取り出し、zscoreで標準化
stats.probplot(stats.zscore(result.resid), dist='norm', plot=plt)
# タイトル、x軸ラベル、y軸ラベルの設定
plt.title('Q-Q Residuals')
plt.ylabel('Standardized residuals');【実行結果】
② lmdiag の q_q
### 別解 lmdiagで描画
plt.figure(figsize=(6, 3))
lmdiag.q_q(result);【実行結果】

③ pingouin の qqplot
### 別解 pingouinで描画
plt.figure(figsize=(6, 3))
pg.qqplot(result.resid, dist='norm', square=False);【実行結果】

どのQ-Qプロットからも、横軸の両端で残差が直線から外れていることが確認できました。
不均一分散の問題点が分かったところで、対策に進んでまいります!

■ 均一分散の仮定が満たされていない場合の対応策
テキストによると分散の不均一性に強い(ロバストな)推定方法の1つ「サンドイッチ推定」を使うことで「残差の等分散性の仮定を満たしていなくても、線形回帰の係数の有効な標準誤差を推定できる」そうです!わーい!
テキストにならって傾きに関するタイプⅠエラー確率算出関数を定義します。
係数のタイプⅠエラーは、傾きが0のときに誤って有意であると判定することです。
傾き=0の指定は、関数実行時に傾き$${\beta_1=0}$$を引数で与えます。
有意水準$${\alpha=5\%}$$です。
サンドイッチ推定に関しては、statsmodelsの sandwich_covariance.cov_white_simple() を用いてサンドイッチ共分散(?)を算出することで対応します。
### 278ページ サンドイッチ推定で線形回帰の係数の有効な標準誤差を推定して
# タイプⅠエラー確率(傾きが0であるときに誤って有意であると判定してしまう確率)を
# シミュレーションする
# シミュレーション関数
def lm_sandwich(n, beta0, beta1, sigma, tau):
## データの作成
# 説明変数の生成
x = rng.uniform(size=n, low=-1, high=1)
# 不均一な残差の生成
e_hetero = rng.normal(size=n, loc=0, scale=np.exp(x * tau))
# 不均一分散の目的変数(理論値)
y_hetero = beta0 + beta1 * x + e_hetero
## 回帰分析の実行
model_hetero = smf.ols(formula='y_hetero ~ x',
data=dict(x=x, y_hetero=y_hetero)).fit()
## 結果の格納
# beta0, beta1のSE
SEs_hetero = model_hetero.bse.values
# sandwich共分散からのSE
# サンドイッチ共分散の算出にstatsmodelsを利用(ただしRのxcovHCと異なる値になる)
SEs_sandwich = np.sqrt(np.diag(
sandwich_covariance.cov_white_simple(model_hetero)))
## 信頼区間の算出
beta1_est = model_hetero.params.values[1], # beta1の推定値
upper_ci = beta1_est + 1.96 * SEs_hetero[1] # 95%信頼区間の上端
lower_ci = beta1_est - 1.96 * SEs_hetero[1] # 95%信頼区間の下端
upper_ci_sand = beta1_est + 1.96 * SEs_sandwich[1] # sand:95%信頼区間の上端
lower_ci_sand = beta1_est - 1.96 * SEs_sandwich[1] # sand:95%信頼区間の下端
## 判定: 信頼区間が0を含まない場合=タイプⅠエラーの場合、1を立てる
flg_lm = np.where(lower_ci < 0 < upper_ci, 0, 1)[0]
flg_sand = np.where(lower_ci_sand < 0 < upper_ci_sand, 0, 1)[0]
## 戻り値
result = np.array([flg_lm, flg_sand])
return resultではシミュレーションを実行しましょう。
シミュレーション回数は 1000 回です。
サンプルサイズ$${n=500}$$、切片$${\beta_0=1}$$、傾き$${\beta_1=0}$$、残差標準偏差$${\sigma=1}$$、残差の大きさの影響力$${\tau=1.5}$$です。
### 279ページ シミュレーションの実行
## 設定と準備
iter = 1000 # シミュレーション回数
n = 500 # サンプルサイズ
beta0 = 1 # 切片
beta1 = 0 # 傾き
simga = 1 # 標準偏差
tau = 1.5 # 残差の大きさの影響力
## 結果を格納するオブジェクト
results = np.zeros((iter, 2))
## シミュレーション
rng = np.random.default_rng(seed=5)
for i in range(iter):
results[i, :] = lm_sandwich(n, beta0, beta1, sigma, tau)
## 結果表示
# 補正しないときのタイプⅠエラー確率
print(f'補正しない場合のタイプⅠエラー確率 :{results[:, 0].mean():.4f}')
# sandwich補正をしたときのタイプⅠエラー確率
print(f'sandwitch補正した場合のタイプⅠエラー確率:{results[:, 1].mean():.4f}')【実行結果】
sandwitch補正を行ったことで、有意水準$${5\%}$$に近似しました。
サンドイッチ推定を用いることで、係数の標準誤差が補正され、タイプⅠエラー確率が適切な値になったことが分かりました。


7.3.2 多重共線性の問題
続いて、「説明変数同士が無相関」という仮定を満たさないことで生じる問題「多重共線性」(通称:マルチコ)に話は移ります。
テキストによるとこの問題は「説明変数同士に強い相関があると係数の標準誤差が大きくなり、係数の推定値の信頼性を大きく損なってしまう問題」です。

■ 説明変数同士に強い相関がある場合の問題点を見える化
「説明変数同士に強い相関があると係数の標準誤差が大きくなる」ことをシミュレーションで見える化します。
まずは関数定義から。
説明変数間の相関係数を指定して、重回帰分析の係数と標準誤差を算出する関数を定義します。
### 280ページ データ作成と重回帰分析を実行し係数と標準誤差を算出する関数
def lm_corr(n, beta1, beta2, sigma, cor):
## 相関係数の入力値チェック
if abs(cor) > 1:
print('相関係数は-1.0から1.0の間で指定してください')
return
## 説明変数の分散共分散行列と説明変数の生成
cov_matrix = np.array([[1, cor], [cor, 1]])
x = rng.multivariate_normal(size=n, mean=[0, 0], cov=cov_matrix)
## 残差の生成
e = rng.normal(size=n, loc=0, scale=sigma)
## 目的変数の生成
y = beta1 * x[:, 0] + beta2 * x[:, 1] + e
## 重回帰分析
model = smf.ols(formula='y ~ x1 + x2',
data=dict(x1=x[:, 0], x2=x[:, 1], y=y)).fit()
## 結果の格納
SEs = model.bse.values
## 戻り値の格納
result = np.array([
model.params.values[1], # beta1
model.params.values[2], # beta2
SEs[1], # beta1のSE
SEs[2], # beta2のSE
])
return result関数の動作確認をします。
サンプルサイズ$${n=1000}$$、係数$${\beta_1=1,\ \beta_2=2}$$、残差標準誤差$${\sigma=3}$$、説明変数間の相関係数$${cor=0.5}$$です。
### 280ページ シミュレーションの動作確認
lm_corr(n=1000, beta1=1, beta2=2, sigma=3, cor=0.5)【実行結果】
左から、係数$${\beta_1,\ \beta_2}$$の推定値、$${\beta_1,\ \beta_2}$$の標準誤差の推定値です。

続いてシミュレーションを実行してデータを作成します。
複数の相関係数のパターンを実行します。
サンプルサイズ$${n=100}$$、係数$${\beta_1=0.5,\ \beta_2=0.7}$$、残差標準誤差$${\sigma=1}$$です。
### 281ページ シミュレーションの実行
## 設定と準備
iter = 1000
# 説明変数間の相関パターン
cor_pattern = [0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 0.95,
0.97, 0.99]
## 結果を格納するオブジェクト
Ln = len(cor_pattern)
results = np.zeros((iter, Ln, 4))
beta1 = np.zeros(Ln)
beta2 = np.zeros(Ln)
se1 = np.zeros(Ln)
se2 = np.zeros(Ln)
## シミュレーション
rng = np.random.default_rng(seed=123)
for i in range(Ln):
for j in range(iter):
results[j, i, :] = lm_corr(
n = 100,
beta1 = 0.5,
beta2 = 0.7,
sigma = 1,
cor = cor_pattern[i]
)
beta1[i] = results[:, i, 0].mean()
beta2[i] = results[:, i, 1].mean()
se1[i] = results[:, i, 2].mean()
se2[i] = results[:, i, 3].mean()
## データフレーム化
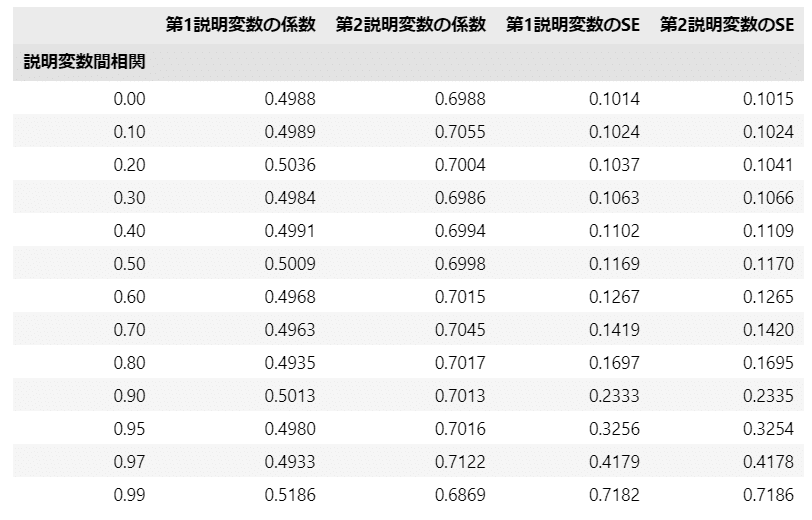
df = pd.DataFrame(results.mean(axis=0),
index=pd.Series(cor_pattern, name='説明変数間相関'),
columns=['第1説明変数の係数', '第2説明変数の係数',
'第1説明変数のSE', '第2説明変数のSE'])
display(df.round(4))【実行結果】
説明変数の係数は$${\beta_1=0.5,\ \beta_2=0.7}$$と近似しているものの、相関係数が大きくなるにつれて係数の標準誤差が大きくなっている様子が分かります。
相関係数の大きさと第1説明変数の係数$${\beta_1}$$の推定値の分布を可視化して確認します。
### 282ページ 図7.9 説明変数間の相関係数と第1説明変数の推定値の分布
# 設定と準備
cors = [0, 0.7, 0.9] # 相関係数のパターン
styles = ['-', '--', ':'] # 相関係数パターンに応じた線種
colors = ['tab:blue', 'tab:green', 'tab:red'] # 相関係数パターンに応じた線色
# 描画領域の設定
fig, ax = plt.subplots(figsize=(6, 3))
# 説明変数1の推定値のカーネル密度推定の描画
for (cor, style, color) in zip(cors, styles, colors) :
# resultsの2次元目の相関係数index値を取得
idx = cor_pattern.index(cor)
# kdeプロットの描画
sns.kdeplot(x=results[:, idx, 0], ls=style, color=color, label=cor, ax=ax)
# 切片の理論値0.5の垂直線の描画
ax.axvline(0.5, color='black')
# x軸範囲、y軸範囲、x軸ラベル、タイトルの設定
ax.set(xlim=(-0.1, 1.1), ylim=(-0.3, 10), xlabel='beta1',
title='density plot of beta1')
# 凡例表示
ax.legend(loc='upper left', title='相関係数');【実行結果】
相関係数が大きくなると係数の標準誤差が大きくなる(平坦になっている)ことが分かります。

テキストでは説明変数間の相関が強くなることで係数の標準誤差が大きくなることの説明が掲載されています。
ぜひテキストをお読みください!

■ VIFによる標準誤差肥大化の程度の診断
VIF(variance inflation factor)を算出して説明変数間の相関の強さを測ってみます。
テキストによると目安は「VIFが 3 、あるいは 10 より大きいと注意が必要です」とのこと。
VIFの式です。$${ r_{12}}$$は2つの説明変数間の相関係数です。
$$
VIF = \cfrac{1}{1 - r^2_{12}}
$$
シミュレーションで用いた相関係数でVIFを算出して、可視化しましょう。
### 284ページ 図7.10 説明変数間の相関係数とVIFの関係
## 設定と準備
r2 = np.array(cor_pattern)**2 # 相関係数の二乗
vif = 1 / (1 - r2) # VIF
## 描画
# 描画領域の設定
plt.figure(figsize=(6, 3))
# 折れ線グラフの描画
plt.plot(r2, vif, '-o', ms=5)
# VIF=10の水平線の描画
plt.axhline(10, color='tab:red', ls='--')
# 修飾
plt.xlabel('説明変数間の相関係数')
plt.ylabel('VIF')
plt.grid(lw=0.5);【実行結果】
$${VIF=10}$$に赤い点線を入れました。
相関係数$${0.9}$$あたりから VIF の値が急激に大きくなる様子が分かります。

シミュレーションデータを用いて、VIF と第1説明変数の係数の標準誤差の関係を可視化します。
### 285ページ 図7.11 VIFと標準誤差の関係
## 設定と準備
r2 = np.array(cor_pattern)**2 # 相関係数の二乗
vif = 1 / (1 - r2) # VIF
## 描画
# 描画領域の設定
plt.figure(figsize=(6, 3))
# 折れ線グラフの描画
plt.plot(vif, se1, '-o', ms=5)
# VIF=10の水平線の描画
plt.axvline(10, color='tab:red', ls='--')
# 修飾
plt.xlabel('VIF')
plt.ylabel('標準誤差')
plt.grid(lw=0.5);【実行結果】
テキストによると「 VIF が標準誤差の増加を反映している指標であることが明らかですね」です。


■ 参考:statsmodels による VIF 計算
statsmodels の variance_inflation_factor() で VIF を計算できます。
この参考コードでは、2つの説明変数と定数項を用いて、VIFを計算しています。
### 参考 statsmodelsでVIF計算
## 設定と準備
# 相関係数のパターンをリスト化
cor_pattern = [0.0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 0.95,
0.97, 0.99]
# 説明変数1のVIF、説明変数2のVIFの計算値を格納する変数
vif_x1 = np.zeros(len(cor_pattern))
vif_x2 = np.zeros(len(cor_pattern))
# 乱数生成器・乱数シード
rng = np.random.default_rng(seed=123)
## 相関係数パターンごとに説明変数を作成してVIFを計算
for i, cor in enumerate(cor_pattern):
## 説明変数の作成
# 分散共分散行列の作成
cov_matrix = np.array([[1, cor], [cor, 1]])
# 説明変数の作成
x = rng.multivariate_normal(size=n, mean=[0, 0], cov=cov_matrix)
# 説明変数に定数項を追加
x_const = np.hstack([x, np.ones(len(x)).reshape(-1, 1)])
## VIFの計算
# 説明変数1のVIF statsmodelsのvariance_inflation_factorを使用
vif_x1[i] = variance_inflation_factor(x_const, 0)
# 説明変数2のVIF
vif_x2[i] = variance_inflation_factor(x_const, 1)
## データフレーム化 2変数のみなので各説明変数のVIFは同値
df = pd.DataFrame(
{'相関係数': cor_pattern, 'VIF_説明変数1': vif_x1, 'VIF_説明変数2': vif_x2,})
display(df)【実行結果】


■ 多重共線性が疑われたときの対応策
テキストは対応策の1つとして「説明変数に主成分分析を行って、説明変数を1つまたは少数の合成変数にまとめること」を取り上げています。
テキスト図7.12を描画してみましょう。
まずは合成関数のないバージョン。
### 286ページ 図7.12上
# 有向グラフオブジェクトの生成 neatoでnodeの位置調整を実施
g = Digraph(engine='neato')
# 基本属性の設定
g.attr('node', shape='box', fontname='Meiryo UI')
g.graph_attr['rankdir'] ='LR'
# 頂点の作成、位置posを設定
g.node('説明変数1', pos='0, 1!')
g.node('説明変数2', pos='0, 0!')
g.node('目的変数', pos='3, 0.5')
# 辺の作成
g.edge('説明変数1', '目的変数')
g.edge('説明変数2', '目的変数')
g.edge('説明変数1', '説明変数2')
g.edge('説明変数2', '説明変数1')
# グラフの描画
g【実行結果】

続いて主成分分析で合成変数を作ったモデルです。
### 286ページ 図7.12下
# 有向グラフオブジェクトの生成
g = Digraph()
# 基本属性の設定
g.attr('node', fontname='Meiryo UI')
g.graph_attr['rankdir'] ='LR'
# 頂点の作成 shapeで形を設定
g.node('説明変数1', shape='box')
g.node('説明変数2', shape='box')
g.node('合成変数', shape='ellipse')
g.node('目的変数', shape='box')
# 辺の作成
g.edge('説明変数1', '合成変数')
g.edge('説明変数2', '合成変数')
g.edge('合成変数', '目的変数')
# グラフの描画
g【実行結果】

主成分分析によって多重共線性の問題を回避する実践に進みましょう。
説明変数間の相関係数は$${-0.9}$$です。強い負の相関です。
### 286ページ 主成分分析によって多重共線性の問題を回避する例
## 設定と準備
rng = np.random.default_rng(seed=0)
n = 100 # サンプルサイズ
beta1 = 0.5 # 回帰係数1
beta2 = 0.7 # 回帰係数2
sigma = 1 # 残差の標準偏差
cor = -0.99 # 説明変数間の相関係数
## データの生成
# 説明変数の分散共分散行列と説明変数の生成
cov_matrix = np.array([[1, cor], [cor, 1]])
x = rng.multivariate_normal(size=n, mean=[0, 0], cov=cov_matrix)
# 残差の生成
err = rng.normal(size=n, loc=0, scale=sigma)
# 目的変数の生成
y = beta1 * x[:, 0] + beta2 * x[:, 1] + err
## 主成分分析による合成関数の作成
# scikit-learnのPCAインスタンスの生成
pca = PCA(n_components=1)
# pcaを実行してxの主成分得点を取得
x_pca = pca.fit_transform(x)
## 回帰分析
# フルモデルで推定した場合
model_full = smf.ols(formula='y ~ x1 + x2',
data=dict(x1=x[:, 0], x2=x[:, 1], y=y)).fit()
# 合成変数で推定した場合
model_pca = smf.ols(formula='y ~ x_pca', data=dict(x_pca = x_pca, y=y)).fit()
## それぞれのモデルの標準誤差
# フルモデル
model_full.bse.to_frame().T【実行結果】
こちらは2つの説明変数が多重共線性を生じさせている(合成変数を使用しない)モデルの係数の標準誤差です。

### 287ページ 続き
# 合成変数モデル
model_pca.bse.to_frame().T【実行結果】
こちらは主成分分析による合成変数を使用したモデルの係数の標準誤差です。
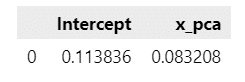
テキストのとおり、係数の標準誤差は「合成変数にすることで」$${0.0832}$$まで下がっています。
合成変数を作ることで、推定値の信頼性が下がる多重共線性の問題を回避しています。
ただし、合成変数のモデルからは、係数の母数$${\beta_1=0.5,\ \beta_2=0.7}$$を推定することはできません…。
今回の写経は以上です。
シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で7つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。
2.実験!たのしいベイズモデリング1&2をPyMC Ver.5で
書籍「たのしいベイズモデリング」・「たのしいベイズモデリング2」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.実験!岩波データサイエンス1のベイズモデリングをPyMC Ver.5で
書籍「実験!岩波データサイエンスvol.1」の4人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう!
4.楽しい写経 ベイズ・Python等
ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀
5.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん!
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。
6.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
7.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
最後までお読みいただきまして、ありがとうございました。
