
10-1-2 重回帰結果の解釈・単回帰予測 ~ 世帯収入と消費支出の回帰モデル
今回の統計トピック
回帰分析テーマの2回目です。
今回は重回帰モデルと単回帰モデルのMIXです。
偏回帰係数の意味、単回帰の予測値に関連する数値の意味を確認します!
引き続き、統計ソフトウェア R に取り組みます!
公式問題集の準備
「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください!
「知る」「実践する」の章で、のんびり統計をお楽しみください!
問題を解く
📘公式問題集のカテゴリ
線形モデルの分野 ~回帰分析の分野
問2 重回帰結果の解釈・単回帰予測(勤労者世帯の1ヶ月の収入・支出)
試験実施年月
統計検定2級 2019年11月 問18(回答番号33,34)
問題
公式問題集をご参照ください。
利用データ
この記事は、問題集が用いる【2017年の都道府県所在市別、2人以上の勤労世帯の1ヶ月の1世帯当たり「世帯収入・支出データ」】を利用しています。
次の図は「世帯収入・支出データ」の抜粋(先頭5行)です。
・単位は「万円」です。
・「世帯主収入合計=定期収入+賞与」です。

【出典記載】
「家計調査(2017年)」(総務省統計局)
(https://www.e-stat.go.jp/stat-search/files?tclass=000000330003&cycle=7&year=20170)
【コンテンツ編集・加工の記載】
記事の記載にあたっては、出典記載の資料を加工して作成しています。

解き方
題意
最小二乗法で推定した2つの回帰モデルについて、次の2問を解答します。
① 重回帰モデルの偏回帰係数の解釈の是非
② 単回帰モデルの予測値に関連する数値の説明の是非
【条件】
■ モデル1:重回帰モデル
・$${消費支出=\alpha_0 + \alpha_1 \times 定期収入 + \alpha_2 \times 賞与 + u}$$
・誤差項$${u}$$は互いに独立に正規分布$${N(0, \sigma^2_u)}$$に従います。
■ モデル2:単回帰モデル
・$${消費支出=\beta_0 + \beta_1 \times 世帯主収入合計 + v}$$
・誤差項$${v}$$は互いに独立に正規分布$${N(0, \sigma^2_v)}$$に従います。
・消費支出$${y}$$の予測値を$${\hat{y}}$$、回帰係数の推定値を$${\hat{\beta_0}, \hat{\beta_1}}$$とするとき、
$${\hat{y}=\hat{\beta_0}+\hat{\beta_1}\times 世帯主収入合計}$$
の平均値$${\bar{\hat{y}}}$$は$${31.3}$$です。
① 重回帰モデル
「世帯収入・支出データ」の重回帰モデルについて、「統計ソフトウェア R の出力結果」は次のようになりました。

設問の1つ目は重回帰モデルの偏回帰係数の意味の出題です。
【回帰式】
上の図の偏回帰係数の推定値「Coefficients - Estimate」から、回帰式を作成しましょう。
$${消費支出=14.58851+0.39461 \times 定期収入 + 0.47247 \times 賞与}$$
【偏回帰係数】
ある説明変数の偏回帰係数は、それ以外の説明変数の値を固定して、ある説明変数の値を1単位増加させたときに、目的変数がどの程度増加するかを示す数値です。
【考察】
定期収入を1万円(1単位)増加させる場合を考えます。
定期収入の偏回帰係数は$${+0.39461}$$です。
定期収入以外の説明変数である賞与の値を固定して、定期収入の値を1万円増加させたときに、目的変数「消費支出」が$${0.39461}$$万円増加するということなのです。

解答選択肢の中で【考察】に合致するのは ① です。
設問1つ目の解答は ① です。
「賞与を一定とすること」と「定期収入が1万円(1単位)増えること」から「消費支出」は定期収入の偏回帰係数、約$${0.39}$$万円(単位)増えるのです。

② 単回帰モデル
「世帯収入・支出データ」の単回帰モデルについて、「統計ソフトウェア R の出力結果」は次のようになりました。

設問の2つ目は単回帰モデルの予測値に関連する3つの問いの是非を解答します。
目的変数である消費支出の予測値の平均値$${\bar{\hat{y}}=31.3}$$にまつわる問題です。
【回帰式】
上の図の回帰係数の推定値「Coefficients - Estimate」から、回帰式を作成しましょう。
$${消費支出=14.3931+0.4121 \times 世帯主収入合計}$$
回帰式をもとにして散布図に回帰直線を描画しましょう。
単回帰モデルは可視化しやすいので、イメージを掴みやすいです!


■ 問Ⅰ:観測データの消費支出の平均$${\bar{y}}$$も$${31.3}$$である。
突然ですが「回帰の主な性質」の降臨です。
「最小二乗法による回帰係数を用いる場合の回帰式の性質 a」をご存知でしょうか?
『a.予測値$${\boldsymbol{\hat{y}_i}}$$の平均値は観測値$${\boldsymbol{y_i}}$$の平均値と等しい』です。
この設問に照らし合わせます。
消費支出の予測値の平均値は$${31.3}$$です。
性質aより、消費支出の予測値の平均値は、消費支出の観測値の平均値と等しいです。
したがって、消費支出の観測値の平均値は$${31.3}$$です。
問Ⅰは適切です。

■ 問Ⅱ:世帯主収入合計の平均は$${41.0}$$である(小数点以下第2位を四捨五入)。
突然ですが「回帰の主な性質」の降臨です。
「最小二乗法による回帰係数を用いる場合の回帰式の性質 c」をご存知でしょうか?
『c.回帰直線は$${\boldsymbol{x,y}}$$の平均点を通る』です。
この設問に照らし合わせます。
問Ⅰの解答より、消費支出の観測値の平均$${\bar{y}}$$は$${31.3}$$です。
回帰式に基づく回帰直線は$${(\bar{x}, 31.3)}$$を通ります。
回帰式に$${\bar{y}=31.3}$$を代入して、世帯主収入合計の平均値$${\bar{x}}$$を求めます。
$$
\begin{align*}
消費支出&=14.3931+0.4121 \times 世帯主収入合計 \\
\bar{y}&=14.3931+0.4121 \times \bar{x} \\
31.3&=14.3931+0.4121 \times \bar{x} \\
0.4121 \times \bar{x} &= 31.3 - 14.3931 \\
0.4121 \times \bar{x} &= 16.9069 \\
\bar{x} &= \cfrac{16.9069}{0.4121} \\
\bar{x} &= 41.02 \cdots \\
\bar{x} &\fallingdotseq 41.0 \cdots
\end{align*}
$$
世帯主収入合計の平均値$${\bar{x}}$$は$${41.0}$$です。
問Ⅱは適切です。

■ 問Ⅲ:各都道府県所在市の予測値$${\hat{y}_i, \quad (i=1, \cdots , 47)}$$に残差を加えると観測データ$${y_i}$$となる。
目的変数の観測値と予測値の差を残差と呼びます。
$${観測値 y_i - 予測値 \hat{y}_i = 残差 e_i}$$です。
この設問に照らし合わせます。
上の式を整理すると、観測値$${y_i}$$は予測値$${\hat{y}_i}$$と残差$${e_i}$$を足した値、になります。
問Ⅲは適切です。
単回帰モデルの問題に関する解答は「ⅠとⅡとⅢはすべて正しい」です。

解答
〔1〕①、〔2〕⑤ です。
難易度 やさしい
・知識:偏回帰係数、回帰の主な性質aとc、予測値と残差
・計算力:数式組み立て(低)、電卓(低)
・時間目安:2問合計 3分
知る
おしながき
公式問題集の問題に接近してみましょう!
今回は「問題を解く」で降臨した謎の「回帰の主な性質」に取り組みます。
単回帰モデル
📕公式テキスト:1.6.4 回帰直線(32ページ~)、5.1.5 線形重回帰モデル(171ページ~)など
特集記事のお知らせ
単回帰モデルの詳しい学習ポイントを「特集記事」にまとめました。
ぜひご覧くださいませ。
回帰の主な性質(4つ)
回帰の主な性質を「世帯収入・支出データ」の重回帰モデルで確認します。
a.予測値の平均値は観測値の平均値と等しい
目的変数の予測値$${\hat{y}}$$の平均値$${\bar{\hat{y}}}$$は、目的変数の観測値$${y}$$の平均値$${\bar{y}}$$と等しいです。
「世帯収入・支出データ」の重回帰モデルに当てはめてみましょう。
すべての説明変数を回帰式「$${消費支出=14.58851+0.39461 \times 定期収入 + 0.47247 \times 賞与}$$」に当てはめて求めた消費支出の予測値の平均値は、消費支出の観測値の平均値と等しい、ということです。
Pythonを電卓代わりにして、このことを確かめましょう!
まず準備です。
次のコードを実行して、消費支出の予測値 result_m.fittedvalues、残差 result_m.resid、回帰係数 result_m.params を取得しておきます。
なお、ライブラリのインポート・データの読み込みの掲載は省略いたします。
### 回帰分析の実行 重回帰モデル:説明変数は定期収入+賞与
result_m = smf.ols('消費支出 ~ 定期収入 + 賞与', data=data).fit()では、消費支出の予測値 result_m.fittedvalues の平均値 y_pred_mean と観測値の平均値 y_mean を計算して、一致するかどうか確かめましょう。
### 回帰の基本的な性質a.目的変数の予測値の平均値は観測値の平均値と等しい
# 予測値の平均値と観測値の平均値の計算
y_pred_mean = result_m.fittedvalues.mean()
y_mean = data["消費支出"].mean()
# 計算結果の表示
print(f'予測値の平均値: {y_pred_mean:.10f}')
print(f'観測値の平均値: {y_mean:.10f}')【実行結果】

予測値の平均値と観測値の平均値は一致しました。
回帰の基本的な性質a「予測値の平均値と観測値の平均値は等しい」を確かめました。
b.残差$${\boldsymbol{e_i=y_i-\hat{y}}}$$の平均は0である
「世帯収入・支出データ」の重回帰モデルに当てはめてみましょう。
すべての説明変数を回帰式「$${消費支出=14.58851+0.39461 \times 定期収入 + 0.47247 \times 賞与}$$」に当てはめて求めた消費支出の予測値と、対応する消費支出の観測値の差「残差=観測値-予測値」の平均値は0、ということです。
Pythonを電卓代わりにして、このことを確かめましょう!
残差 result_m.resid の平均値を計算して0になることを確かめます。
### 回帰の基本的な性質b.残差の平均値は0である
# 残差の平均値の計算
resid_mean = result_m.resid.mean()
# 計算結果の表示
print(f'残差の平均値: {resid_mean:.10f}')【実行結果】

残差の平均値は0になりました!
(コンピュータ計算における小数端数処理の関係で、完全な0にはなりません)
回帰の基本的な性質b「残差の平均値は0である」を確かめました。
c.回帰式は$${\boldsymbol{x_1, \cdots, x_p,y}}$$の平均点を通る
「世帯収入・支出データ」の重回帰モデルに当てはめてみましょう。
回帰式「$${消費支出=14.58851+0.39461 \times 定期収入 + 0.47247 \times 賞与}$$」に消費支出の平均値、定期収入の平均値、賞与の平均値を当てはめた求めた「$${消費支出の平均値=14.58851+0.39461 \times 定期収入の平均値 + 0.47247 \times 賞与の平均値}$$」が成り立つ、ということです。
Pythonを電卓代わりにして、このことを確かめましょう!
回帰式に定期収入の平均値と賞与の平均値を当てはめて求めた消費支出の予測値が、消費支出の平均値と一致することを確かめます。
2段目の回帰式に含む result_m.params[0] 等は、回帰係数です。
### 回帰の基本的な性質c.回帰式は説明変数と目的変数の平均値の点を通る
# 説明変数の平均値の算出
x1_mean = data['定期収入'].mean()
x2_mean = data['賞与'].mean()
# 回帰式に説明変数の平均値を当てはめて目的変数を予測する
y_calc_mean = result_m.params[0] + result_m.params[1]*x1_mean \
+ result_m.params[2]*x2_mean
# 計算結果の表示
print(f'消費支出の予測値: {y_calc_mean:.10f}')
print(f'消費支出の平均値: {y_mean:.10f}')【実行結果】

消費支出の予測値は消費支出の平均値と一致しました。
回帰の基本的な性質c「回帰式は説明変数と目的変数の平均点を通る」を確かめました。
ちなみに、説明変数が2つの重回帰モデルの回帰式は「回帰平面」(2次元)になります。
説明変数が1つの単回帰モデルの場合の「回帰直線」(1次元)ですので、説明変数が2つになると2次元になるのです!
次の図は消費支出の重回帰モデルのグラフです。

薄赤色の平面が回帰平面、赤い点が観測値です。
中央付近の青い星印は平均点です。
d.予測値$${\boldsymbol{\hat{y_i}}}$$と残差$${\boldsymbol{e_i}}$$の相関係数は0である
「世帯収入・支出データ」の重回帰モデルに当てはめてみましょう。
回帰式「$${消費支出=14.58851+0.39461 \times 定期収入 + 0.47247 \times 賞与}$$」で求めた消費支出の「予測値」と、消費支出の観測値と予測値の差である「残差」との間の相関係数は0、ということです。
Pythonを電卓代わりにして、このことを確かめましょう!
予測値 result_m.fittedvalues と残差 result_m.resid の相関係数を計算します。
相関係数の計算には、numpy の corrcoef 関数を用いています。
### 回帰の基本的な性質d.目的変数の予測値と残差の相関係数は0である
# 相関係数の計算
r_yp_e = np.corrcoef(result_m.fittedvalues, result_m.resid)
# データフレーム形式で計算結果を表示
names = ['予測値', '残差']
pd.DataFrame(r_yp_e, index=names, columns=names).round(10)【実行結果】

予測値と残差の相関行列が表示されました。
予測値と残差が交差するセルは「0.0」です。
つまり、予測値と残差の相関係数は0ということです!
(コンピュータ計算における小数端数処理の関係で、完全な0にはなりません)
回帰の基本的な性質d「予測値と残差の相関係数は0である」を確かめました。
以上で4つの性質を確認しました。
統計検定2級の公式テキスト173ページに重回帰モデルの場合の性質が証明付きで掲載されています。
ぜひ、読んでくださいね!
実践する
世帯収入・支出データの2つの回帰分析を実践する
世帯収入・支出データを用いて2つの回帰分析を実践しましょう!
EXCEL、R、Pythonの3つの手段でトライします。
先頭バッターのEXCELの出力結果を用いて、2つのモデルを比較したり、回帰式の考察をしたいと思います!
特集記事のお知らせ
EXCEL、R、Pythonの単回帰分析の実践を「特集記事」にまとめました。
ぜひご覧くださいませ。
CSVファイルのダウンロード
こちらのリンクから「世帯収入・支出データ」のCSVファイルをダウンロードできます。
EXCELで作成してみよう!
データ分析アドインを利用する
EXCELの「データ分析」アドインを用いて回帰分析を実践します。
「データ」メニューに「データ分析」が無い場合は、データ分析のアドインを有効にしましょう。
メニューより、「ファイル」>「オプション」を選びます。
「Excelのオプション」画面の左メニュー「アドイン」を指定します。
「Excelのオプション」画面の下部の「管理」で「Excelアドイン」を選び、「設定」ボタンをクリックします。
「アドイン」画面で「分析ツール」をチェックして、OKボタンをクリックします。
操作概要
■ メニューで「データ分析」を指定します。
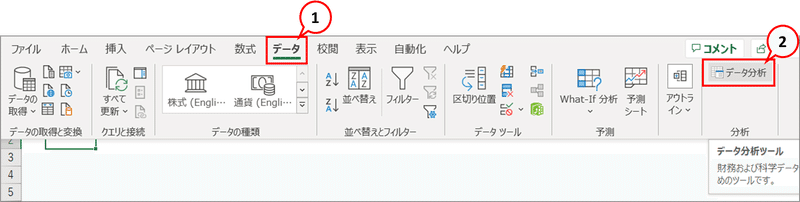
■ 「データ分析」画面で「回帰分析」を選びます。

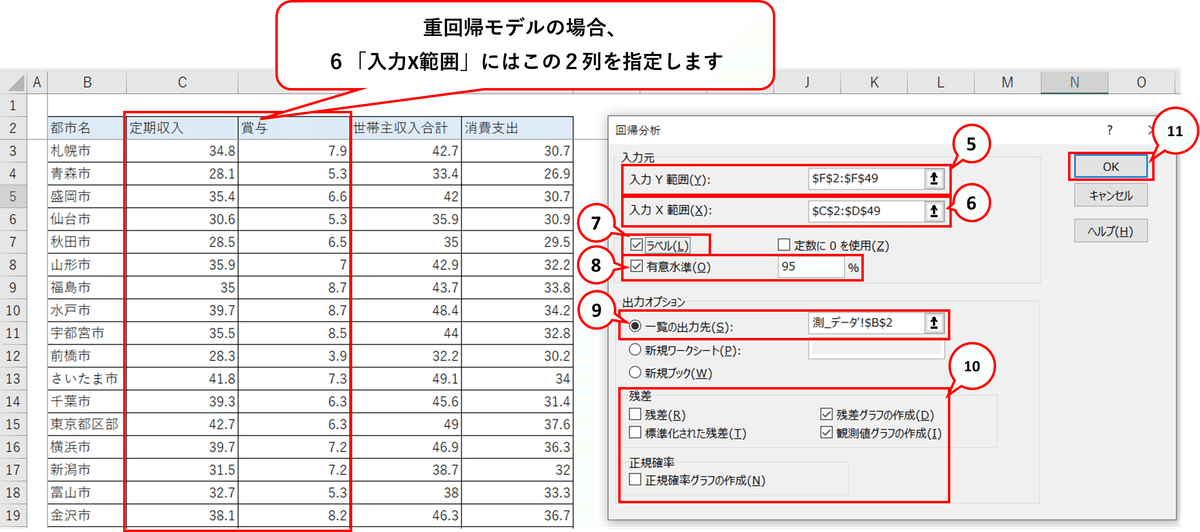
■ 「回帰分析」画面でx、yデータの指定等を行います。
この操作を終えると、分析結果が表示されます。
重回帰モデルの出力結果

回帰式は次のようになりました。
$${消費支出=14.5885 + 0.3946 \times 定期収入 + 0.4725 \times 賞与}$$
単回帰モデルの出力結果

回帰式は次のようになりました。
$${消費支出=14.3931 + 0.4121 \times 世帯主収入合計}$$
2つのモデルの比較
$$
\begin{array}{c|c:c:c}
モデル & 回帰の有意性検定のp値 & 回帰係数の検定のp値& R^{*2} \\
\hline
重回帰 & 0.0000 &定期収入:0.0001 & 0.5161 \\
& & 賞与:0.0590 & \\
& & 切片:0.0000 & \\
\hdashline
単回帰 & 0.0000 & 世帯主収入合計:0.0000 & 0.5261 \\
& & 切片:0.0000 & \\
\end{array}
$$
両方のモデルは$${F}$$値の$${p}$$値が極小であり、有意水準$${5\%}$$で、このモデルに含まれる説明変数の中に目的変数の説明に役立つ変数がある、と言えるでしょう。
回帰係数に関しては、重回帰モデルの賞与の回帰係数の$${p}$$値が$${5\%}$$を超えており、有意水準$${5\%}$$で、賞与は回帰係数が0であるという帰無仮説を棄却できないです。
自由度調整済み決定係数$${R^{*2}}$$は単回帰モデルの方がやや大きい値を取っています。
自由度調整済み決定係数でモデルを選択する場合には、値の大きい単回帰モデルが選択されるでしょう。
「世帯収入・支出データ」の収入と支出の関係の考察
今回の世帯収入・支出データは、定期収入も賞与も支出も「1ヶ月あたり」に平均化されています。
例えばデータが12月の収入・支出に限定されていれば、12月賞与が支出に与える影響はかなり多いでしょう。
しかし、データの収入・支出は1ヶ月に「均されて」います。
つまり、「賞与が出たから支出を増やそう」という行動がデータに反映されにくくなっていることでしょう。
だから、単回帰モデルのように「収入合計」にまとめるほうが、収入と支出の回帰の関係を明確に示せるような気がします。
EXCELサンプルファイルのダウンロード
こちらのリンクからEXCELサンプルファイルをダウンロードできます。
サンプルファイルには「世帯収入・支出データ」が含まれています。
R で作成してみよう!
R スクリプトで回帰分析を実践します。
手順③④で、問題文中に使用される「統計ソフトウェアの出力結果」を作成しています。
数値の解釈は「EXCELで作成してみよう!」の「2つのモデルの比較」を参考にしてください。
① データの読み込み
### データの読み込み
data <- read.csv("sampledata.csv")
# データの要約表示
str(data)
summary(data)【出力結果】
世帯収入・支出データの概要を表示しました。
> str(data)
'data.frame': 47 obs. of 5 variables:
$ 都市名 : chr "札幌市" "青森市" "盛岡市" "仙台市" ...
$ 定期収入 : num 34.8 28.1 35.4 30.6 28.5 35.9 35 39.7 35.5 28.3 ...
$ 賞与 : num 7.9 5.3 6.6 5.3 6.5 7 8.7 8.7 8.5 3.9 ...
$ 世帯主収入合計: num 42.7 33.4 42 35.9 35 42.9 43.7 48.4 44 32.2 ...
$ 消費支出 : num 30.7 26.9 30.7 30.9 29.5 32.2 33.8 34.2 32.8 30.2 ...
> summary(data)
都市名 定期収入 賞与 世帯主収入合計
Length:47 Min. :27.60 Min. :2.800 Min. :32.00
Class :character 1st Qu.:31.60 1st Qu.:5.750 1st Qu.:38.00
Mode :character Median :34.70 Median :6.500 Median :41.20
Mean :34.27 Mean :6.657 Mean :40.93
3rd Qu.:36.20 3rd Qu.:7.800 3rd Qu.:43.85
Max. :42.70 Max. :9.200 Max. :51.20
消費支出
Min. :24.60
1st Qu.:29.80
Median :31.40
Mean :31.26
3rd Qu.:32.80
Max. :37.60② 相関係数の表示
### 相関係数の計算
cor(data[, seq(2,5)])【出力結果】
定期収入 賞与 世帯主収入合計 消費支出
定期収入 1.0000000 0.5895499 0.9715618 0.7053814
賞与 0.5895499 1.0000000 0.7640439 0.5764775
世帯主収入合計 0.9715618 0.7640439 1.0000000 0.7324073
消費支出 0.7053814 0.5764775 0.7324073 1.0000000③ 回帰分析の実行 重回帰モデル
lm 関数を用いて、回帰モデルのformula(式)を組み立てて、回帰分析を実行します。
formula(式)は「目的変数 ~ 説明変数」の形式で記述します。
### 回帰分析の実施と結果表示 モデル1
data.lm1 <- lm(消費支出 ~ 定期収入+賞与, data=data)
summary(data.lm1)【実行結果】
出ました!「統計ソフトウェアの出力結果」です。
Call:
lm(formula = 消費支出 ~ 定期収入 + 賞与, data = data)
Residuals:
Min 1Q Median 3Q Max
-4.6362 -1.1512 0.0681 1.2958 3.3035
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 14.58851 2.49814 5.840 5.80e-07 ***
定期収入 0.39461 0.08944 4.412 6.54e-05 ***
賞与 0.47247 0.24370 1.939 0.059 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.898 on 44 degrees of freedom
Multiple R-squared: 0.5371, Adjusted R-squared: 0.5161
F-statistic: 25.53 on 2 and 44 DF, p-value: 4.371e-08④ 回帰分析の実行 単回帰モデル
### 回帰分析の実施と結果表示 モデル2
data.lm2 <- lm(消費支出 ~ 世帯主収入合計, data=data)
summary(data.lm2)【実行結果】
Call:
lm(formula = 消費支出 ~ 世帯主収入合計, data = data)
Residuals:
Min 1Q Median 3Q Max
-4.589 -1.119 0.066 1.345 3.249
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 14.3931 2.3531 6.117 2.09e-07 ***
世帯主収入合計 0.4121 0.0571 7.216 4.88e-09 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 1.878 on 45 degrees of freedom
Multiple R-squared: 0.5364, Adjusted R-squared: 0.5261
F-statistic: 52.07 on 1 and 45 DF, p-value: 4.879e-09⑤ 散布図の描画
パッケージ psych を用いて、各変数の組み合わせ一式で散布図を表示します。
インストールする場合は、次のコードの2行目の # を取って実行してみてください。
### 散布図行列の描画 by psych
# install.packages("psych")
library(psych)
psych::pairs.panels(data[, seq(2,5)])【実行結果】

⑥ 分散分析の実行 重回帰モデル
### 分散分析の実施と結果表示 モデル1
anova(data.lm1)【出力結果】
Analysis of Variance Table
Response: 消費支出
Df Sum Sq Mean Sq F value Pr(>F)
定期収入 1 170.423 170.423 47.2954 1.731e-08 ***
賞与 1 13.544 13.544 3.7587 0.05897 .
Residuals 44 158.548 3.603
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1⑦ 分散分析の実行 単回帰モデル
### 分散分析の実施と結果表示 モデル2
anova(data.lm2)【出力結果】
Analysis of Variance Table
Response: 消費支出
Df Sum Sq Mean Sq F value Pr(>F)
世帯主収入合計 1 183.73 183.732 52.071 4.879e-09 ***
Residuals 45 158.78 3.529
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Rサンプルファイルのダウンロード
こちらのリンクからRスクリプト形式のサンプルファイルをダウンロードできます。
Pythonで作成してみよう!
statsmodels を用いて回帰分析を実践します。
手順⑤⑥で、問題文中に使用される「統計ソフトウェアの出力結果」に近いアウトプットを作成しています。
数値の解釈は「EXCELで作成してみよう!」の「2つのモデルの比較」を参考にしてください。
① インポート
### インポート
# 数値計算
import numpy as np
import pandas as pd
# 統計処理
import statsmodels.api as sm
import statsmodels.formula.api as smf
# 可視化
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'② データの読み込み
世帯収入・支出データをpandasのデータフレームに読み込み、データの形状と先頭5行を表示します。
### データの読み込み
data = pd.read_csv(r'sampledata.csv', index_col=0)
print('data.shape', data.shape)
display(data.head())【実行結果】

「都市名」はインデックスです。
③ 要約統計量の表示
pandas の describe で最小値・最大値・平均値・四分位数等を表示します。
なお、数値の小数点以下の丸めは「.round()」で指定します。
### 要約統計量の表示
data.describe().round(2)【実行結果】

④ 相関係数の表示
pandas の corr で日本小売価格と世界総生産量の相関係数を計算します。
### 相関行列の表示
data.corr().round(3)【出力結果】

最下行の消費支出を見ましょう。
目的変数である消費支出と、説明変数である収入項目の相関係数を確認できます。
世帯主収入収入合計との相関係数の値が最も大きく、$${0.732}$$です。
⑤ 回帰分析の実行 重回帰モデル
smf.ols でモデル model1 を定義します。
R スクリプトと同様に、formula(数式)形式で「目的変数 ~ 説明変数」を定義します(クォーテーションでくくる点が R と異なります)。
model1 に対して fit を実行することで回帰分析が行なえます。
### 回帰モデルの定義と実行 モデル1:定期収入+賞与
# モデルの定義
model1 = smf.ols('消費支出 ~ 定期収入 + 賞与', data=data)
# 回帰分析の実行
result1 = model1.fit()
# 回帰分析の結果を表示
result1.summary()【実行結果】

⑥ 回帰分析の実行 単回帰モデル
### 回帰モデルの定義と実行 モデル2:世帯主収入合計
# モデルの定義
model2 = smf.ols('消費支出 ~ 世帯主収入合計', data=data)
# 回帰分析の実行
result2 = model2.fit()
# 回帰分析の結果を表示
result2.summary()【実行結果】
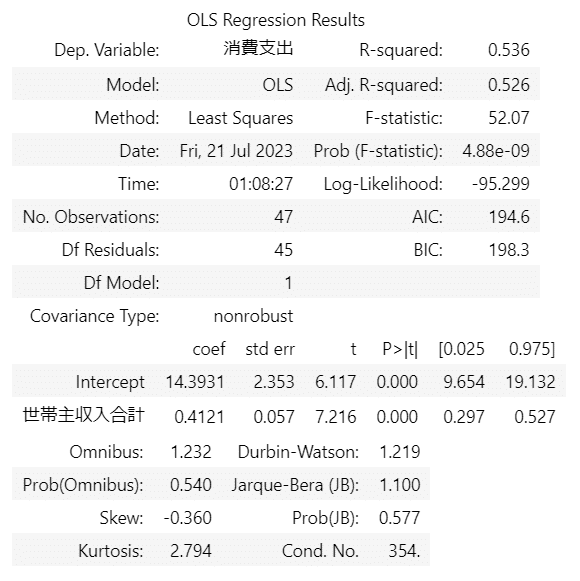
⑦ 散布図と回帰直線の描画
seaborn の pairplot を利用して、散布図行列を作成します。
### 散布図行列の描画
sns.pairplot(data, kind='reg', height=2, corner=True, # corner:右上を非表示
# 散布図の設定
plot_kws={'ci': False, # 信頼区間を非表示
'scatter_kws': {'alpha': 0.4}, # 色の透過性
'line_kws': {'color': 'red', # 線:赤色、幅1
'lw': 1}},
# ヒストグラムの設定
diag_kws={'alpha': 0.7, # 色の透過性
'ec': 'white'}); # 枠線:白色【実行結果】

定期収入のヒストグラムは中央の柱と左右の裾のギャップが大きい印象です。
⑧ 分散分析の実行 重回帰モデル
分散分析の関数 sm.stats.anova_lm を用いて回帰分析結果の分散分析を行います。
anova_lm に与えるデータは、回帰分析の結果 result1 です。
分散分析の実行の下の数行は合計行を表示するコードです。
### 分散分析表の表示 モデル1
# 分散分析の実行
anova1 = sm.stats.anova_lm(result1, typ=1)
# 合計行の作成
anova1_sum = anova1.sum(axis=0).to_frame(name='合計').T
anova1_sum.iloc[0, 2:] = np.nan
# 合計行をデータフレームに結合
anova1 = pd.concat([anova1, anova1_sum], axis=0)
# 分散分析表の表示
anova1.round(4)【実行結果】

⑨ 分散分析の実行 単回帰モデル
### 分散分析表の表示 モデル2
# 分散分析の実行
anova2 = sm.stats.anova_lm(result2, typ=1)
# 合計行の作成
anova2_sum = anova2.sum(axis=0).to_frame(name='合計').T
anova2_sum.iloc[0, 2:] = np.nan
# 合計行をデータフレームに結合
anova2 = pd.concat([anova2, anova2_sum], axis=0)
# 分散分析表の表示
anova2.round(4)【実行結果】

Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。
おわりに
今回は2変数の重回帰モデルと単回帰モデルの2つに取り組みました。
世帯収入・支出データのもととなる家計調査(2017年)のダウンロードデータ(.xlsファイル)には、「貯蓄純増(平均貯蓄率)(%)」という項目があります、
最大値は福井市 33.9%、最小値は秋田市 12.8%でした。
最後までお読みいただきまして、ありがとうございました。
のんびり統計シリーズの記事
次の記事
前の記事
目次
