
「数値シミュレーションで読み解く統計のしくみ」をPythonで写経 ~ 第6章6.3「サンプルサイズ設計の実践」
第6章「適切な検定のためのサンプルサイズ設計」
書籍の著者 小杉考司 先生、紀ノ定保礼 先生、清水裕士 先生
この記事は、テキスト「数値シミュレーションで読み解く統計のしくみ」第6章「適切な検定のためのサンプルサイズ設計」の6.3節「サンプルサイズ設計の実践」の Python写経活動 を取り扱います。
第6章はシミュレーションを通じて、調査・実験の事前段階でサンプルサイズを設計する方法を学びます。
今回は2つのt検定のサンプルサイズ設計を学びます。
非心t分布と仲良しになります!

R の基本的なプログラム記法はざっくり Python の記法と近いです。
コードの文字の細部をなぞって、R と Python の両方に接近してみましょう!
ではテキストを開いてシミュレーションの旅に出発です🚀
はじめに
テキスト「数値シミュレーションで読み解く統計のしくみ」のご紹介
このシリーズは書籍「数値シミュレーションで読み解く統計のしくみ〜Rでためしてわかる心理統計」(技術評論社、「テキスト」と呼びます)の Python写経です。
テキストは、2023年9月に発売され、副題「Rでためしてわかる心理統計」のとおり、統計処理に定評のある R の具体的なコードを用いて、心理統計の理解に役立つ数値シミュレーションを実践する素晴らしい書籍です。
引用表記
この記事は、出典に記載の書籍に掲載された文章及びコードを引用し、適宜、掲載文章とコードを改変して書いています。
【出典】
「数値シミュレーションで読み解く統計のしくみ〜Rでためしてわかる心理統計」初版第1刷、著者 小杉考司・紀ノ定保礼・清水裕士、技術評論社
記事中のイラストは、「かわいいフリー素材集いらすとや」さんのイラストをお借りしています。
ありがとうございます!
6.3 サンプルサイズ設計の実践
1標本のt検定と、対応のない2標本のt検定のサンプルサイズ設計を実践します。
Pythonで必要サンプルサイズを計算する際には、ぜひ、pingouin ライブラリをご利用ください!
記事では「アディショナルタイム」で pingouin を用いたサンプルサイズ設計のコードを掲載しています。

この記事は Jupyter Notebook 形式(拡張子 .ipynb)でPythonコードを書きます。
概ね確率分布の特性値算出には scipy.stats を用い、乱数生成には numpy.random.generator を用いるようにしています。
主に利用するライブラリをインポートします。
### インポート
# 数値計算
import numpy as np
# 確率・統計
import scipy.stats as stats
from statsmodels.stats import power # サンプルサイズ
import pingouin as pg # 統計便利ツール
# 描画
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Meiryo'タイプⅠエラー確率とタイプⅡエラー確率の描画関数を定義します。
### タイプⅠエラー確率とタイプⅡエラー確率の描画関数
def plot_statistical_error(lambda_, df, alpha, i, n=None):
# 描画領域の設定
plt.figure(figsize=(6, 3))
# t分布の描画
x = np.linspace(-3, 7, 1001)
plt.plot(x, stats.t.pdf(x, df=df), color='tab:orange', linestyle='--')
# 帰無分布の描画
# 臨界値から8までの値を200区切りで用意
xx = np.linspace(stats.t.ppf(q=1 - alpha / 2, df=df), 7, i)
yy = stats.t.pdf(xx, df=df) # xxに対応したt分布の密度を得る
# タイプⅠエラー確率を色付け
plt.fill_between(xx, yy, color='tab:orange', ec='gray', alpha=0.2,
label='タイプⅠエラー確率')
# 非心分布の描画
plt.plot(x, stats.nct.pdf(x, df=df, nc=lambda_), color='tab:blue')
# -3から臨界値までの値を200区切りで用意
xx = np.linspace(-3, stats.t.ppf(q=1 - alpha / 2, df=df), i)
yy = stats.nct.pdf(xx, df=df, nc=lambda_) # xxに対応した非心t分布の密度を得る
# タイプⅡエラー確率を色付け
plt.fill_between(xx, yy, color='tab:blue', ec='gray', alpha=0.2,
label='タイプⅡエラー確率')
# タイトルの設定
if n is None:
title = f'非心度={lambda_}のときの\nタイプⅠエラー確率とタイプⅡエラー確率'
else:
title = f'n={n}のときのタイプⅡエラー確率'
plt.title(title)
# x軸ラベル、y軸ラベル、凡例の設定
plt.xlabel('x')
plt.ylabel('Density')
plt.legend()
plt.show()
6.3.1 1標本のt検定のサンプルサイズ設計
1標本のt検定のサンプルサイズ設計に取り組みます!
テキストにならって、非心t分布でタイプⅡエラー確率を計算して、あらかじめ設定したタイプⅡエラー確率の許容値$${\beta}$$未満になるように、非心度を調整して、サンプルサイズを設計します。
テキストに掲載の5つのステップを踏んで進めてまいります。
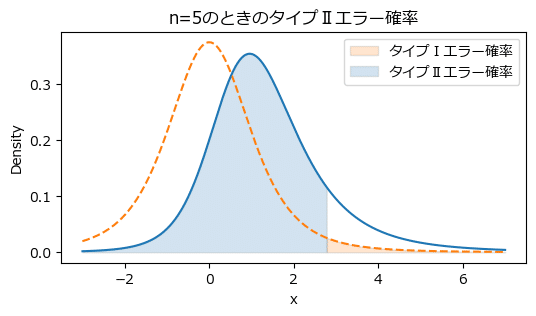
■ サンプルサイズ$${n=5}$$のタイプⅡエラー確率
有意水準$${\alpha=5\%}$$、タイプⅡエラー確率の閾値$${\beta=20\%}$$、効果量$${\delta_0=0.5}$$でタイプⅡエラー確率を計算します。
### 239ページ 1標本のt検定のサンプルサイズ設計
## 設定と準備
alpha = 0.05 # 有意水準
beta = 0.20 # タイプⅡエラー確率の閾値(この値未満に抑えたい)
delta = 0.5 # 見積もった効果量
# 1.最初に定めたサンプルサイズ
n = 5
# 2.非心度λの計算
lambda_ = delta * np.sqrt(n)
# 3.1.自由度の計算
df = n -1
# 3.2.臨界値の計算: t分布のパーセント点
cv = stats.t.ppf(q=1 - alpha/2, df=df)
# 4.タイプⅡエラー確率の計算: 非心t分布の累積分布関数
type2_error = stats.nct.cdf(x=cv, df=df, nc=lambda_)
# タイプⅡエラー確率の出力
type2_error【実行結果】

タイプⅡエラー確率は$${86\%}$$となり、$${\beta=20\%}$$を大きく上回っています。
可視化してタイプⅠエラー確率、タイプⅡエラー確率を確認してみます。
# 240ページ 図6.6
# 帰無分布(点線)の臨界値が非心分布(青い線)のエラー確率の上端になる
plot_statistical_error(lambda_, df, alpha, 200, n)【実行結果】
テキストに合わせて、1標本のt検定のタイプⅡエラー確率計算を関数化します。
### 240ページ 1標本のt検定のタイプⅡエラー確率算出関数
def t2e_ttest(alpha, delta, n):
# 2.非心度λの計算
lambda_ = delta * np.sqrt(n)
# 3.1.自由度の計算
df = n -1
# 3.2.臨界値の計算: t分布のパーセント点
cv = stats.t.ppf(q=1 - alpha/2, df=df)
# 4.タイプⅡエラー確率の計算: 非心t分布の累積分布関数
type2_error = stats.nct.cdf(x=cv, df=df, nc=lambda_)
# 戻り値: タイプⅡエラー確率、描画のため非心度と自由度も返す
return type2_error, lambda_, df
■ サンプルサイズ$${n=10, 15, 20}$$のタイプⅡエラー確率
サンプルサイズを少しづつ増やして、タイプⅡエラー確率の変化を確認します。
徐々にタイプⅡエラー確率の値が小さくなります。
$${n=10}$$のケースです。
### 240ページ 1標本のt検定のサンプルサイズ設計 n=10
## 設定と準備
alpha = 0.05 # 有意水準
beta = 0.20 # タイプⅡエラー確率の閾値(この値未満に抑えたい)
delta = 0.5 # 見積もった効果量
# n=10の場合
n = 10
type2_error, lambda_, df = t2e_ttest(alpha, delta, n)
type2_error【実行結果】

# 描画
plot_statistical_error(lambda_, df, alpha, 200, n)【実行結果】

$${n=15}$$のケースです。
### 241ページ n=15の場合
n = 15
type2_error, lambda_, df = t2e_ttest(alpha, delta, n)
type2_error【実行結果】

# 描画
plot_statistical_error(lambda_, df, alpha, 200, n)【実行結果】

$${n=20}$$のケースです。
### 241ページ n=20の場合
n = 20
type2_error, lambda_, df = t2e_ttest(alpha, delta, n)
type2_error【実行結果】

# 描画
plot_statistical_error(lambda_, df, alpha, 200, n)【実行結果】


■ 閾値$${\beta = 20\%}$$になるまでfor文でサンプルサイズを増やす
for文でサンプルサイズを増やして(上限 10000)、タイプⅡエラー確率の閾値$${\beta = 20\%}$$以下になるサンプルサイズを探索します。
### 241ページ 1標本のt分布のサンプルサイズ・シミュレーション
## 設定と準備
alpha = 0.05 # 有意水準
beta = 0.20 # タイプⅡエラー確率の閾値(この値未満に抑えたい)
delta = 0.5 # 見積もった効果量
iter = 10000 # シミュレーション回数
## シミュレーション
# タイプⅡエラー確率が閾値β以下になるまでサンプルサイズを増やす(上限10000)
for n in range(5, iter+1):
# サンプルサイズnのときのタイプⅡエラー確率を算出
type2_error, lambda_, df = t2e_ttest(alpha, delta, n)
# タイプⅡエラー確率が閾値β以下になったらシミュレーションを終了
if type2_error <= beta:
break
## 結果
# 条件を満たすn
print(f'必要サンプルサイズ: {n}')
# タイプⅡエラー確率
print(f'タイプⅡエラー確率: {type2_error:.7f}')【実行結果】
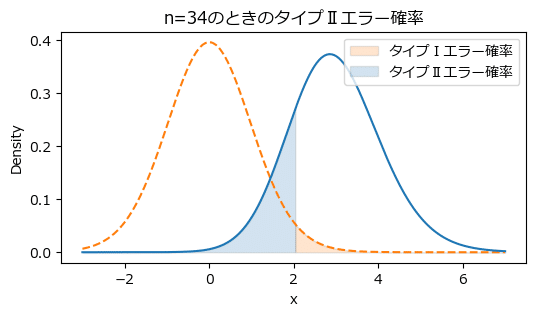
サンプルサイズ$${n=34}$$のとき、タイプⅡエラー確率は$${19.2\%}$$になりました!

サンプルサイズ$${n=34}$$のときのタイプⅠエラー確率とタイプⅡエラー確率を可視化しましょう。
# 描画
plot_statistical_error(lambda_, df, alpha, 200, n)【実行結果】

アディショナルタイム1
テキストから少々離れて、ここからはアディショナルタイムに突入です!
Pythonのライブラリを用いてサンプルサイズ計算を行います。
■ アディショナルタイム①「pingouinのpower_ttest」
pingouin ライブラリを用いて必要サンプルサイズを計算します。
### 別解 pingouinのpower_ttestで必要サンプルサイズを算出
## 設定と準備
alpha = 0.05 # 有意水準
beta = 0.20 # タイプⅡエラー確率の閾値
delta = 0.5 # 見積もった効果量
## 算出
n = np.ceil(pg.power_ttest(d=delta, power=1 - beta, alpha=alpha,
contrast='one-sample', alternative='two-sided'))
n【実行結果】
テキストの計算結果と同じになりました!

サンプルサイズ$${n=34}$$のときのタイプⅡエラー確率を計算します。
### 別解 続き pingouinのpower_ttestで必要サンプルサイズのタイプⅡエラー確率を算出
1 - pg.power_ttest(d=delta, n=n, alpha=alpha, contrast='one-sample',
alternative='two-sided')【実行結果】
テキストの計算結果とほぼほぼ同じになりました!

■ アディショナルタイム②「statsmodelsのtt_solve_power」
statsmodels ライブラリを用いて必要サンプルサイズを計算します。
### 別解 statsmodelsのtt_solve_powerで必要サンプルサイズを算出
## 設定と準備
alpha = 0.05 # 有意水準
beta = 0.20 # タイプⅡエラー確率の閾値
delta = 0.5 # 見積もった効果量
## 算出
n = np.ceil(power.tt_solve_power(effect_size=delta, alpha=alpha, power=1-beta,
alternative='two-sided'))
n【実行結果】
テキストの計算結果と同じになりました!

サンプルサイズ$${n=34}$$のときのタイプⅡエラー確率を計算します。
### 別解 続き statsmodelsのtt_solve_powerで必要サンプルサイズのタイプⅡエラー確率算出
1- power.tt_solve_power(effect_size=delta, nobs=n, alpha=alpha,
alternative='two-sided')【実行結果】
テキストの計算結果とほぼほぼ同じになりました!


6.3.2 対応のないt検定
続いて対応のない2標本のt検定のサンプルサイズ設計に取り組みます!
対応のない2標本のt検定の場合の非心度について、テキストの数式をお借りします。
$$
\lambda = \delta_0 \sqrt{\ \left( \cfrac{n_1 n_2}{n_1 + x}\right)\ }
$$
テキストに合わせて、対応のない2標本のt検定のタイプⅡエラー確率計算を関数化します。
### 243ページ 対応のない2標本のt検定のタイプⅡエラー確率算出関数の定義
def t2e_ttest_ind(alpha, delta, n1, n2):
# 自由度の計算
df = n1 + n2 - 2
# 非心度の計算
lambda_ = delta * np.sqrt((n1 * n2) / (n1 + n2))
# 臨界値の計算
cv = stats.t.ppf(q=1 - alpha / 2, df=df)
# タイプⅡエラー確率の計算
type2_error = stats.nct.cdf(x=cv, df=df, nc=lambda_)
return type2_error
■ 閾値$${\beta = 20\%}$$になるまでfor文でサンプルサイズを増やす
for文でサンプルサイズを増やして(上限 10000)、タイプⅡエラー確率の閾値$${\beta = 20\%}$$以下になるサンプルサイズを探索します。
2群のサンプルサイズの決め方は、テキストにならって、$${n_1}$$に対する$${n_2}$$の比率を決める方法を採用します。
このシミュレーションでは比率 ratio = 1 です。
### 243ページ 対応のない2標本のt検定のサンプルサイズ・シミュレーション
## 設定と準備
alpha = 0.05 # 有意水準
beta = 0.20 # タイプⅡエラー確率の閾値(この値未満に抑えたい)
delta = 0.5 # 見積もった効果量
ratio = 1 # n1に対するn2の大きさを表す比率
iter = 10000 # シミュレーション回数
## シミュレーション
# タイプⅡエラー確率が閾値β以下になるまでサンプルサイズを増やす(上限10000)
for n1 in range(5, iter+1):
# n2の算出
n2 = np.ceil(n1 * ratio) # np.ceil()は正の無限大への切り上げ
# サンプルサイズn1, n2のときのタイプⅡエラー確率を算出
type2_error = t2e_ttest_ind(alpha, delta, n1, n2)
# タイプⅡエラー確率が閾値β以下になったらシミュレーションを終了
if type2_error <= beta:
break
## 結果
# 必要サンプルサイズ
print(f'必要サンプルサイズ: {n1 + n2:.0f}')
# タイプⅡエラー確率
print(f'タイプⅡエラー確率: {type2_error:.7f}')【実行結果】
テキストの必要サンプルサイズとタイプⅡエラー確率と一致しています。
テキスト曰く「128人という意外に大きいサンプルが必要であることがわかります」です。


アディショナルタイム2
またまたテキストから少々離れて、ここからはアディショナルタイムに突入です!
Pythonのライブラリを用いて、対応のない2標本のt検定に関するサンプルサイズ計算を行います。
■ アディショナルタイム①「pingouinのpower_ttest」
pingouin ライブラリを用いて必要サンプルサイズを計算します。
1標本のときとの違いは、contrast 引数に two-samples (2標本)を与える点です。
### 別解 pingouinのpower_ttestで必要サンプルサイズを算出
# サンプルサイズが異なるケースでは必要サンプルサイズを算出できない感じ
## 設定と準備
alpha = 0.05 # 有意水準
beta = 0.20 # タイプⅡエラー確率の閾値
delta = 0.5 # 見積もった効果量
## 必要サンプルサイズの算出
n = np.ceil(pg.power_ttest(d=delta, power=1 - beta, alpha=alpha,
contrast='two-samples', alternative='two-sided'))
n * 2【実行結果】
テキストの計算結果と同じになりました!

サンプルサイズ$${n=128}$$のときのタイプⅡエラー確率を計算します。
### 別解 続き pingouinのpower_ttestで必要サンプルサイズのタイプⅡエラー確率
1 - pg.power_ttest(d=delta, n=n, alpha=alpha, contrast='two-samples',
alternative='two-sided')【実行結果】
テキストの計算結果とほぼほぼ同じになりました!

■ アディショナルタイム②「statsmodelsのtt_ind_solve_power」
statsmodels ライブラリを用いて必要サンプルサイズを計算します。
1標本のときとの違いは、tt_ind_solve_power 関数を用いる点です。
### 別解 statsmodelsのtt_ind_solve_powerで必要サンプルサイズを算出
## 設定と準備
alpha = 0.05 # 有意水準
beta = 0.20 # タイプⅡエラー確率の閾値(この値未満に抑えたい)
delta = 0.5 # 見積もった効果量
ratio = 1 # n1に対するn2の大きさを表す比率
## 算出
n = np.ceil(power.tt_ind_solve_power(effect_size=delta, alpha=alpha, ratio=ratio,
power=1-beta, alternative='two-sided'))
n * 2【実行結果】
テキストの計算結果と同じになりました!

サンプルサイズ$${n=128}$$のときのタイプⅡエラー確率を計算します。
### 別解 続き statsmodelsのtt_ind_solve_powerで
# 必要サンプルサイズのタイプⅡエラー確率を算出
1- power.tt_ind_solve_power(effect_size=delta, nobs1=n, alpha=alpha, ratio=ratio,
alternative='two-sided')【実行結果】
テキストの計算結果とほぼほぼ同じになりました!

今回の写経は以上です。
シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で7つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。
2.実験!たのしいベイズモデリング1&2をPyMC Ver.5で
書籍「たのしいベイズモデリング」・「たのしいベイズモデリング2」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.実験!岩波データサイエンス1のベイズモデリングをPyMC Ver.5で
書籍「実験!岩波データサイエンスvol.1」の4人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう!
4.楽しい写経 ベイズ・Python等
ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀
5.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん!
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。
6.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
7.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
最後までお読みいただきまして、ありがとうございました。
