
時系列分析入門【第4章 その2】レベル・トレンド・季節成分を持つ状態空間モデルをPythonとPyMC Ver.5 で実践する
この記事は、テキスト「RとStanではじめる 心理学のための時系列分析入門」の第4章「RStanによる状態空間モデル」のRスクリプト・Stanコードをお借りして、PythonとPyMC Ver.5 で「実験的」に実装する様子を描いた統計ドキュメンタリーです。
取り扱いテーマは3つの状態空間モデルです。
レベルの変化のみを考慮したローカルレベルモデル
レベルの変化に加えて傾きの変化も考慮したローカル線形トレンドモデル
季節成分を考慮したローカルレベルモデル
PyMCのGaussianRandomWalk(ランダムウォーク)とAR(自己回帰モデル)、および、pymc_experimental.statespaceの状態空間モデルを適宜組み合わせてモデリングします。
【おことわり】
生成する乱数データがテキストと一致しないため、この記事で利用するデータや推論結果がテキストと一致しないことを予めお断りいたします。
テキストの紹介、引用表記、シリーズまえがきは、このリンクの記事をご参照ください。
テキストで使用するデータは、R・Stan等のサンプルスクリプトで指定されています。
サンプルスクリプトは著者GitHubサイトからダウンロードして取得できます。
第4章 RStanによる状態空間モデル
この記事は「4.2 観測値が連続量の場合」の4.2.1~4.2.2を実践いたします。
インポート(+環境準備)
この記事で用いるライブラリをインポートします。
### インポート
# 基本
import numpy as np
import pandas as pd
# PyMC
import pymc as pm
import pytensor.tensor as pt
from pymc_experimental.statespace import structural as st
import arviz as az
# グラフ描画
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Meiryo'
# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')【補足】PyMC環境の構築
AnacondaでPyMC環境を構築する方法を次のリンクの「pymc環境の構築」の箇所に記載しています。
ご参考まで。
【補足】pymc_experimentalのインストール
pymc_experimentalの公式サイトに掲載のインストール方法は、Gitリポジトリからインストールする方法です。
そこで、まずGitアプリをインストールして、次にpymc_experimentalをインストールします。
■ Gitアプリのインストール
私はこちらのサイトからGitアプリをダウンロードしました。
Windows版のインストールの手順は、こちらのサイトの情報を参考にしました。
■pymc_experimentalのインストール
pymc_experimental公式サイトのインストールコードをそのまま実行しました。
pip install git+https://github.com/pymc-devs/pymc-experimental.git
状態空間モデルを構成する要素
テキストによる状態空間モデル検討の要点を以下に引用いたします。
「真の状態」を表すシステムモデル(状態方程式)と観測された観測値に関する観測モデル(観測方程式)を組み合わせることで直接観測できないパラメータを推定します。
システムモデル検討で大切なことは、時系列データの成分の捉え方です。
時系列データ=レベル成分+トレンド成分+季節成分+外因性成分+誤差
飛行機乗客数データセット「AirPassengers」の季節分解データを用いて、レベル成分・トレンド成分・季節成分を図にしてみました。

この記事では、レベル成分、トレンド成分、季節成分を考慮してモデリングを行い、100か月の観測値から20か月先の予測を実施します。
データの準備
テキストの仮想データを作成します。
12ヶ月周期の季節性を持つ100か月のデータです。
### 仮想データの作成 ※図4.10に相当
# 初期値設定
np.random.seed(1111)
N = 100 # 期間
mu_0 = 0 # 状態初期値
mu_T = 0 # トレンドの平均値
sigma_O = 0.1 # 観測ノイズの標準偏差
sigma_W = 0.1 # システムノイズの標準偏差
sigma_T = 0.1 # トレンドの標準偏差
mu = np.zeros(N)
## muの算出
# muの初期値
mu[0] = mu_0
# 傾きtrend
trend = np.random.normal(loc=mu_T, scale=sigma_T, size=N-1)
# muの算出
for i in range(1, N):
mu[i] = np.random.normal(loc=mu[i-1]+trend[i-1], scale=sigma_W, size=1)
# 周期性pの算出
# 周期成分を適当に作成し、これを季節成分とする
# 12か月周期のフーリエ級数の第2調和まで考慮している
# 100か月分の周期成分を作成
p = np.zeros(N)
t = np.arange(1, 13)
for i in range(1, 3):
p = np.tile((np.random.random()*2-1) * np.cos(i*t) \
+ (np.random.random()*2-1) * np.sin(i*t), N//len(t)+1
)[:N] + p
# 目的変数の算出
y = np.random.normal(loc=mu+p, scale=sigma_O, size=N)
# データフレーム化
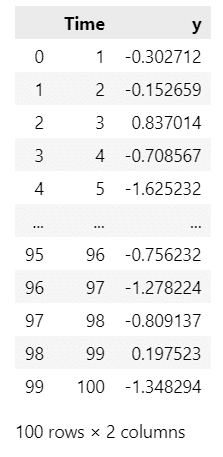
df_ss = pd.DataFrame({'Time': range(1, N+1), 'y': y})
display(df_ss)【実行結果】
グラフ描画します。
### 描画
plt.figure(figsize=(10, 3))
plt.plot(df_ss['Time'], df_ss['y'])
plt.xlabel('Time')
plt.ylabel('y')
plt.show()【実行結果】
おおきなうねりと小刻みな12か月周期を持つデータになりました。

20期先予測に用いるデータを作成します。
先に作成した仮想データの後ろに欠損値を配置しています。
### 将来予測用データの作成(予測期間を考慮)
# 予測期間
pred_period = 20
# 観測データ+予測期間データの生成
y_fore = np.concatenate([df_ss['y'].values, np.repeat(np.nan, pred_period)])
idx_fore = np.concatenate(
[df_ss.index, np.arange(df_ss.index[-1]+1, df_ss.index[-1]+pred_period+1)])
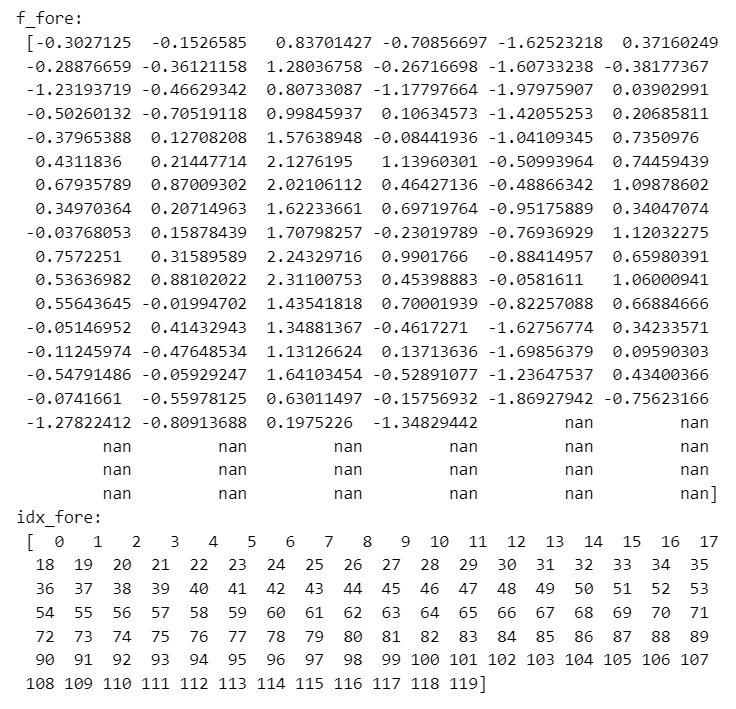
print('f_fore:\n', y_fore)
print('idx_fore:\n', idx_fore)【実行結果】

レベル変化のみを考慮したローカルレベルモデル
真の状態$${\mu_t}$$と観測値$${y_t}$$のシンプルな関係です。
$$
\begin{align*}
\mu_t &= \mu_{t-1} + \varepsilon_t, \quad \varepsilon_t \sim \text{Normal}\ (0,\ \sigma^2_{\varepsilon}) \cdots システムモデル\\
y_t &= \mu_t + \xi_t, \quad \xi_t \sim \text{Normal}\ (0,\ \sigma^2_{\xi}) \cdots 観測モデル\\
\end{align*}
$$
このローカルレベルモデルでは、次の3つのモデルを試みます。
システムモデル(状態方程式)にガウスランダムウォークを適用
システムモデル(状態方程式)に自己回帰モデルAR(1)を適用
状態空間モデル専用のモデルを適用
1.ガウスランダムウォーク
状態方程式にpymcのGaussianRandomWalkを用いるモデルです。
次のリンクでPyMC公式サイトのGaussianRandomWalkのページを開けます。
① モデルの定義
状態「mu」 に pm.GaussianRandomWalk()を用います。
観測値+予測に用いるデータには欠損値が含まれるため、ConstantDataでの読み込みが(私の知るところでは)エラーになります。
尤度関数のobservedで観測値+予測用の欠損値データを読み込みます。
### モデルの定義
# モデルの定義
with pm.Model() as model_rw1:
### データ関連定義
# coordの定義
model_rw1.add_coord('data', values=idx_fore, mutable=True)
# # dataの定義 ※欠損値を含んだデータは定義できない
# y = pm.ConstantData('y', value=y_fore, dims='data')
### 事前分布
sigmaS = pm.HalfCauchy('sigmaS', beta=5)
sigmaO = pm.HalfCauchy('sigmaO', beta=5)
### muの計算
init_dist = pm.Normal.dist(mu=0, sigma=100)
mu = pm.GaussianRandomWalk('mu', sigma=sigmaS, init_dist=init_dist,
dims='data')
### 尤度
likelihood = pm.Normal('likelihood', mu=mu, sigma=sigmaO, observed=y_fore,
dims='data')【実行結果】出力なし
② モデルの可視化
# モデルの可視化
pm.model_to_graphviz(model_rw1)【実行結果】
100か月の観測値「observed」と20ヶ月の予測対象「unobserved」が尤度や$${\mu}$$の120か月のdataと関係している様子が分かります。

③ 事後分布からのサンプリング
MCMCを実行します。
データに欠損値を含むため、PyMC標準のサンプラーを使用します。
実行時間はおよそ7分35秒でした。
### 事後分布からのサンプリング ※欠損値を含む→PyMC標準のサンプラー 7分35秒
with model_rw1:
idata_rw1 = pm.sample(draws=2000, tune=2000, chains=4, target_accept=0.9,
random_seed=1234)【実行結果】

④ サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.1}$$としています。
### r_hat>1.1の確認
# 設定
idata_in = idata_rw1 # idata名
threshold = 1.1 # しきい値
# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in).to_dataframe() > threshold).sum())【実行結果】
$${\hat{R}>1.1}$$のパラメータは「0」件です。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

パラメータ等の事後分布の要約統計量です。
### 推論データの要約統計情報の表示
pm.summary(idata_rw1, hdi_prob=0.95)【実行結果】
一部抜粋となります。

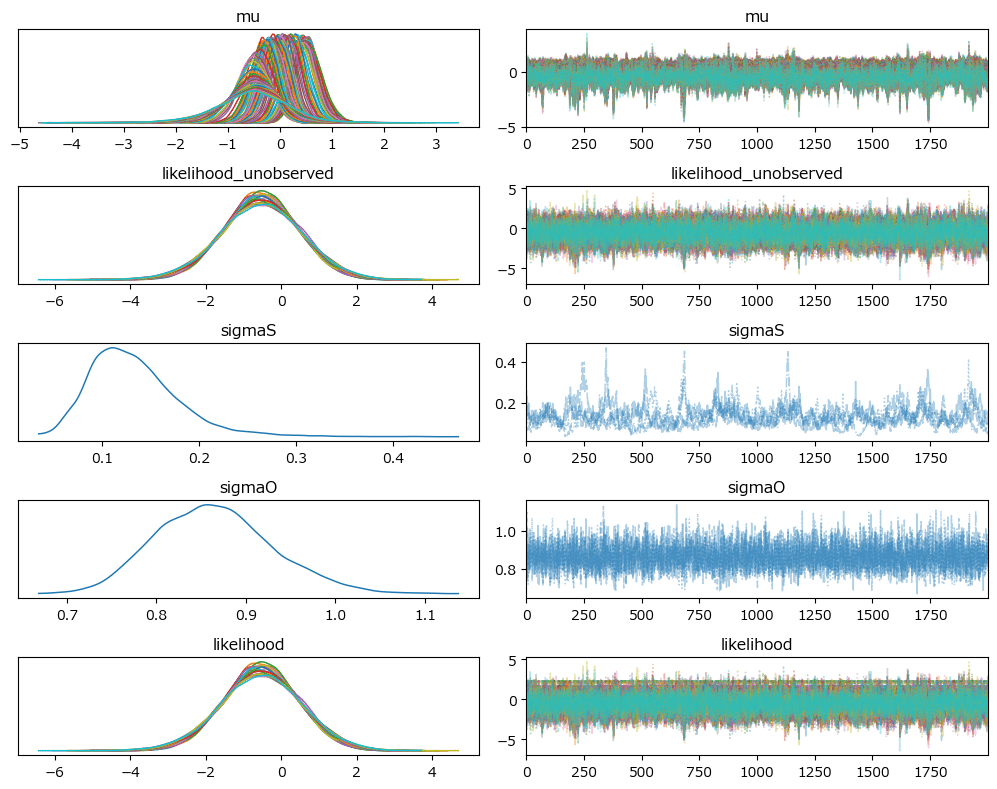
トレースプロットを確認しましょう。
### トレースプロットの表示
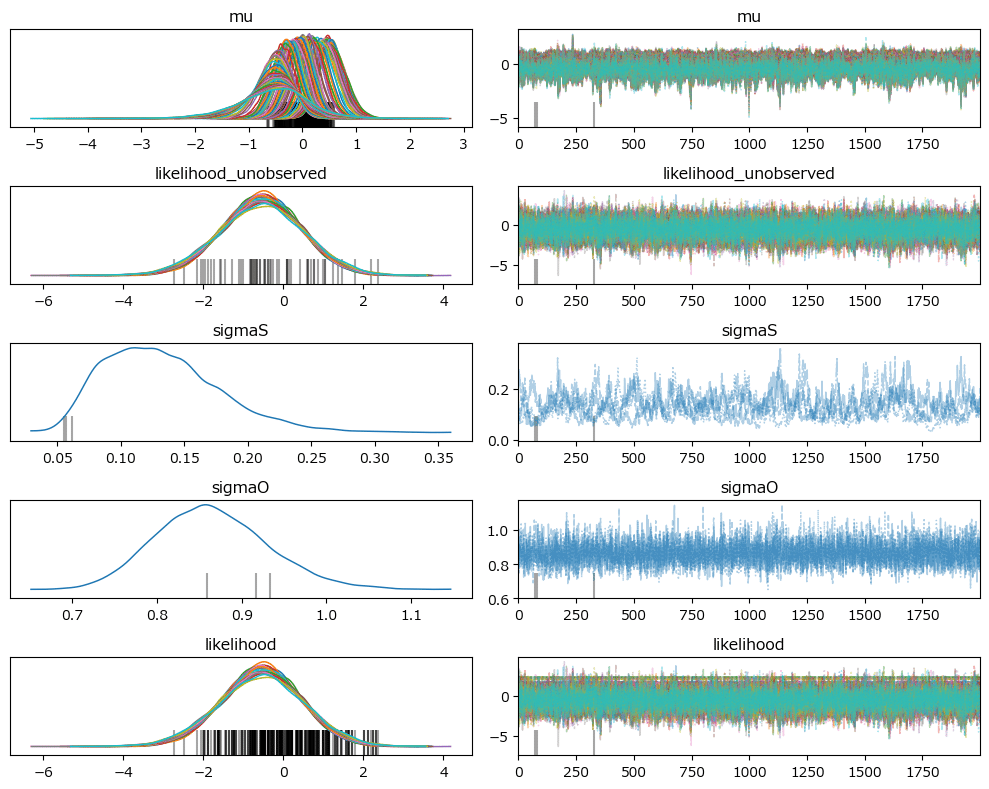
pm.plot_trace(idata_rw1, combined=True, figsize=(10, 8))
plt.tight_layout();【実行結果】
収束している感じがします。
発散のバーコードが見られます。
⑤ 真の状態$${\boldsymbol{\mu}}$$を描画
状態「mu」の事後平均値と80%HDI・50%HDI区間を描画します。
テキストの図4.11上に相当します。
同じ処理を何度か実行しますので、描画処理を関数化いたします。
### muの事後分布の平均値、50%・80%HDI区間の描画関数の定義
def plot_mu_posterior(idata):
## 事後平均・80%HDI・50%HDIの算出
tmp = idata.posterior
mean = tmp.mu.stack(sample=('chain', 'draw')).mean(axis=1).data
hdi80 = az.hdi(tmp, hdi_prob=0.80).mu.data
hdi50 = az.hdi(tmp, hdi_prob=0.50).mu.data
## 描画
fig, ax = plt.subplots(figsize=(10, 3))
# 100日の垂直線の描画
ax.axvline(100, color='black', lw=0.8, ls='--')
# 観測値の描画
ax.scatter(df_ss['Time'], df_ss['y'], color='blue', s=8, label='観測値')
## 観測期間
# 事後平均の描画
ax.plot(df_ss['Time'], mean[:len(df_ss)], color='tab:blue',
label='事後平均')
# 80%HDI区間の描画
ax.fill_between(df_ss['Time'], hdi80[:len(df_ss), 0], hdi80[:len(df_ss), 1],
color='tab:blue', alpha=0.15, label='HDI 80%')
# 50%HDI区間の描画
ax.fill_between(df_ss['Time'], hdi50[:len(df_ss), 0], hdi50[:len(df_ss), 1],
color='tab:blue', alpha=0.4, label='HDI 50%')
## 予測期間
# 予測平均の描画
ax.plot(idx_fore[len(df_ss)-1:]+1, mean[len(df_ss)-1:], color='red',
label='予測平均')
# 80%HDI区間の描画:予測期間
ax.fill_between(idx_fore[len(df_ss)-1:]+1, hdi80[len(df_ss)-1:, 0],
hdi80[len(df_ss)-1:, 1], color='tomato', alpha=0.15,
label='HDI 80%')
# 50%HDI区間の描画:予測期間
ax.fill_between(idx_fore[len(df_ss)-1:]+1, hdi50[len(df_ss)-1:, 0],
hdi50[len(df_ss)-1:, 1], color='tomato', alpha=0.4,
label='HDI 50%')
# 修飾
ax.set(xlabel='Time', ylabel='$\mu$ EAP')
ax.grid(lw=0.3)
ax.legend(bbox_to_anchor=(1.18, 1))
plt.show()描画処理を実行します。
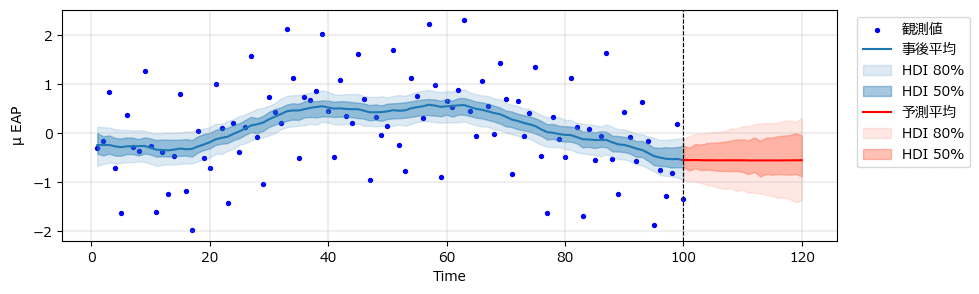
### muの事後分布のプロット ★図4.11に相当
plot_mu_posterior(idata_rw1)【実行結果】
0付近をゆったりと漂う感じです。
レベル成分のみ考慮するモデルであり、赤い予測は単純な横ばいになっています。
⑥ 観測される$${\boldsymbol{y}}$$の事後予測を描画
目的変数「y」の事後予測を行って描画します。
### 事後予測のサンプリングの実施
with model_rw1:
idata_rw1.extend(pm.sample_posterior_predictive(idata_rw1))【処理結果】省略
「y」の事後予測サンプリングデータを描画します。
描画処理を関数化します。
### yの事後予測の平均値、50%・80%HDI区間の描画関数の定義
def plot_posterior_pred(idata):
## 事後平均・80%HDI・50%HDIの算出
tmp = idata.posterior_predictive
mean = tmp.likelihood.stack(sample=('chain', 'draw')).mean(axis=1).data
hdi80 = az.hdi(tmp, hdi_prob=0.80).likelihood.data
hdi50 = az.hdi(tmp, hdi_prob=0.50).likelihood.data
## 描画
fig, ax = plt.subplots(figsize=(10, 3))
# 100日の垂直線の描画
ax.axvline(100, color='black', lw=0.8, ls='--')
# 観測値の描画
ax.scatter(df_ss['Time'], df_ss['y'], color='blue', s=8, label='観測値')
## 観測期間
# 事後平均の描画
ax.plot(df_ss['Time'], mean[:len(df_ss)], color='tab:blue',
label='事後平均')
# 80%HDI区間の描画
ax.fill_between(df_ss['Time'], hdi80[:len(df_ss), 0], hdi80[:len(df_ss), 1],
color='tab:blue', alpha=0.15, label='HDI 80%')
# 50%HDI区間の描画
ax.fill_between(df_ss['Time'], hdi50[:len(df_ss), 0], hdi50[:len(df_ss), 1],
color='tab:blue', alpha=0.4, label='HDI 50%')
## 予測期間
# 予測平均の描画
ax.plot(idx_fore[len(df_ss)-1:]+1, mean[len(df_ss)-1:], color='red',
label='予測平均')
# 80%HDI区間の描画:予測期間
ax.fill_between(idx_fore[len(df_ss)-1:]+1, hdi80[len(df_ss)-1:, 0],
hdi80[len(df_ss)-1:, 1], color='tomato', alpha=0.15,
label='HDI 80%')
# 50%HDI区間の描画:予測期間
ax.fill_between(idx_fore[len(df_ss)-1:]+1, hdi50[len(df_ss)-1:, 0],
hdi50[len(df_ss)-1:, 1], color='tomato', alpha=0.4,
label='HDI 50%')
# 修飾
ax.set(xlabel='Time', ylabel='$y$')
ax.grid(lw=0.3)
ax.legend(bbox_to_anchor=(1.18, 1))
plt.show()描画処理を実行します。
### yの事後予測のプロット
plot_posterior_pred(idata_rw1)【実行結果】


2.自己回帰AR(1)
状態方程式にpymcのARを用いるモデルです。
ランダムウォークは、次数1・切片$${\rho_0=0}$$・自己回帰係数$${\rho_1=1}$$の自己回帰モデル「AR(1)過程」です。
次のリンクでPyMC公式サイトのARのページを開けます。
① モデルの定義
状態「mu」 に pm.AR()を用います。
「constant=False」で切片$${\rho_0}$$が無いことを指定します。
「rho=1」で次数分の自己回帰係数を指定します。
今回は次数1ですので係数は1個であり、自己回帰係数の値$${\rho_1=1}$$を指定します。
### モデルの定義
# モデルの定義
with pm.Model() as model_ar1:
### データ関連定義
# coordの定義
model_ar1.add_coord('data', values=idx_fore, mutable=True)
# # dataの定義 ※欠損値を含んだデータは定義できない
# y = pm.ConstantData('y', value=df_ss['y'].values, dims='data')
### 事前分布
sigmaS = pm.HalfCauchy('sigmaS', beta=5)
sigmaO = pm.HalfCauchy('sigmaO', beta=5)
### muの計算
init_dist = pm.Normal.dist(mu=0, sigma=100)
mu = pm.AR('mu', rho=1, sigma=sigmaS, constant=False, init_dist=init_dist,
ar_order=1, dims='data')
### 尤度
likelihood = pm.Normal('likelihood', mu=mu, sigma=sigmaO, observed=y_fore,
dims='data')【実行結果】出力なし
② モデルの可視化
# モデルの可視化
pm.model_to_graphviz(model_ar1)【実行結果】
ガウスランダムウォークを用いたモデルと類似しています。

③ 事後分布からのサンプリング
MCMCを実行します。
データに欠損値を含むため、PyMC標準のサンプラーを使用します。
実行時間はおよそ6分10秒でした。
### 事後分布からのサンプリング ※欠損値を含む→PyMC標準のサンプラー 6分10秒
with model_ar1:
idata_ar1 = pm.sample(draws=2000, tune=2000, chains=4, target_accept=0.9,
random_seed=1234)【実行結果】

④ サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.1}$$としています。
### r_hat>1.1の確認
# 設定
idata_in = idata_ar1 # idata名
threshold = 1.1 # しきい値
# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in).to_dataframe() > threshold).sum())【実行結果】
$${\hat{R}>1.1}$$のパラメータは「0」件です。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

パラメータ等の事後分布の要約統計量です。
### 推論データの要約統計情報の表示
pm.summary(idata_ar1, hdi_prob=0.95)【実行結果】

トレースプロットを確認しましょう。
### トレースプロットの表示
pm.plot_trace(idata_ar1, combined=True, figsize=(10, 8))
plt.tight_layout();【実行結果】
収束している感じがします。
ガウスランダムウォークとは異なって、発散のバーコードが見られなくなりました。
⑤ 真の状態$${\boldsymbol{\mu}}$$を描画
状態「mu」の事後平均値と80%HDI・50%HDI区間を描画します。
テキストの図4.11中に相当します。
### muの事後分布のプロット ★図4.11に相当
plot_mu_posterior(idata_ar1)【実行結果】
ぱっと見では、ガウスランダムウォークとほぼ同様に見えます。

⑥ 観測される$${\boldsymbol{y}}$$の事後予測を描画
目的変数「y」の事後予測を行って描画します。
### 事後予測のサンプリングの実施
with model_ar1:
idata_ar1.extend(pm.sample_posterior_predictive(idata_ar1))【処理結果】省略
描画処理を実行します。
### yの事後予測のプロット
plot_posterior_pred(idata_ar1)【実行結果】
ぱっと見では、ガウスランダムウォークとほぼ同様に見えます。


3.状態空間モデル
pymc_experimental.statespaceを用いるモデルです。
pymc_experimentalは、正式なpymc機能になる前の「実験段階のモジュール」を扱うパッケージです。
次のリンクでpymc_experimental公式サイトの状態空間モデルのページを開けます。
状態空間モデルでは将来予測用の機能があります。
そこで、欠損値を含む予測用データを用いず、100か月分の観測値(実測値)データでモデルを構築します。
構築したモデルで目的変数$${y}$$の20か月将来予測(forecast)を実施します。
この方法を実践することにより、図4.11に相当する真の状態$${\mu}$$の将来予測の描画を省略いたします。
① モデルの定義
2段階でモデルを定義します。
1段階目は状態空間モデルの定義です。
pymc_experimental.statespaceを用いています。
### 状態空間モデルの定義
# レベル・トレンド成分の定義
# μt = μt-1 + εt, εt ~ Normal(0, σε²)
trend = st.LevelTrendComponent(order=1, innovations_order=1)
# 測定ノイズの定義 分散パラメータσv²
error = st.MeasurementError(name='obs')
# レベル・トレンド成分と観測ノイズで状態空間モデルを構築
ss_model1 = (trend + error).build(name='local1')【補足】
■ LevelTrendComponent
ローカルレベルモデルは、状態方程式が「レベル成分」に相当します。
LevelTrendComponent=レベル・トレンド成分で状態方程式を定義します。
引数のorder、innovations_orderの意味合いはややこしいのですが、公式サイトのガウスランダムウォーク事例に従って、それぞれ1を設定します。
時系列変数が1個かつ1次であること(order=1)、状態のノイズが1個であること(innovations_order=1)のようです。
■ MeasurementError
観測方程式の観測ノイズです。
■ (trend + error).build()
前半のカッコ内は、状態方程式を定義した trend と観測ノイズを定義した error を足して、観測方程式を完成させています。
build()は、状態空間モデルを構築するおまじないです。
【実行結果】
PyMCモデルの定義で設定の必要な「パラメータ」を指示してくれます。
指示通りのパラメータ名を用いて、形状、制約(正の数など)、次元を設定します。

では2段階目のPyMCモデルを定義しましょう。
### PyMCモデルの定義
with pm.Model(coords=ss_model1.coords) as model_ss1:
## パラメータの事前分布
# 初期値の標準偏差
P0 = pm.HalfCauchy('P0', beta=5, dims=['state', 'state_aux'])
# レベル・トレンド成分の初期値
intitial_trend = pm.Normal('initial_trend', mu=0, sigma=100,
dims=['trend_state'])
# 状態変数の標準偏差
sigma_trend = pm.HalfCauchy('sigma_trend', beta=5, dims=['trend_shock'])
sigma_obs = pm.HalfCauchy('sigma_obs', beta=5)
## 状態空間モデルの計算グラフ構築
ss_model1.build_statespace_graph(data=df_ss['y'], mode='JAX')【実行結果】出力なし
【補足】
P0、initial_trend、sigma_trend、sigma_obsは状態空間モデルの定義時に指示のあったパラメータです。
P0:(おそらく)何かの初期値の標準偏差に使われる模様です(推測)。
適切な設定値(お作法)がわからないので、ひとまず半コーシー分布にしました。initial_trend:レベル・トレンド成分の初期値と思われます。
ガウスランダムウォークや自己回帰モデルの状態「mu」の初期分布と同じ内容にしました。sigma_trend:状態のノイズ(システムノイズ)です。ガウスランダムウォークや自己回帰モデルのsigmaUの事前分布と同じ内容にしました。
sigma_obs:観測ノイズです。ガウスランダムウォークや自己回帰モデルのsigmaVの事前分布と同じ内容にしました。
「状態空間モデルの計算グラフ構築」の「ss_mod.build_statespace_graph」では、PyMCモデルの諸パラメータを使って状態空間モデル ss_mod の状態空間モデルの計算グラフ(pymcの内部構造)を生成する、こんな感じのことをしていると想像いたします。
② モデルの表示・可視化
パラメータ(変数)の名前に「_」(アンダースコア)を含むため、自環境ではTeXのエラーが発生してしまいます。
そこで、__getstate__()で内部構造を赤裸々にします!
### モデルの表示()
model_ss1.__getstate__()【実行結果】
途中省略されたモデル内部の情報です。
読み解けません(泣)

図による可視化ならば読み解きしやすいかもです。
# モデルの可視化
pm.model_to_graphviz(model_ss1)【実行結果】
読み解けません(泣)
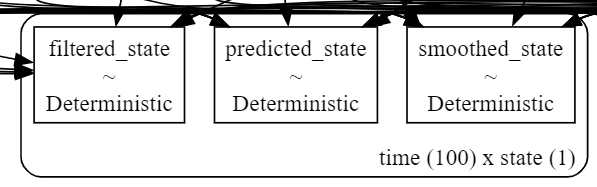
四角ボックスの決定論的変数がおそらく、数学的な状態空間モデルに現れる各種変数と思われます。

ちなみに次の部分が「状態」です。
たぶん、状態空間モデルの「予測」predicted、「フィルタ」filtered、「平滑化」smoothedだと思われます。
③ 事後分布からのサンプリング
ここからは通常のPyMCモデルと同様の処理になります。
ではMCMCを実行しましょう!
NUTSサンプラーにnumpyroを使用するので爆速です(のはずです)。
実行時間は約1分15秒でした。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 1分15秒
with model_ss1:
idata_ss1 = pm.sample(draws=2000, tune=2000, chains=4, target_accept=0.9,
nuts_sampler='numpyro', random_seed=1234)【実行結果(一部分)】

④ サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.1}$$としています。
### r_hat>1.1の確認
# 設定
idata_in = idata_ss1 # idata名
threshold = 1.1 # しきい値
# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in).to_dataframe() > threshold).sum())【実行結果】
$${\hat{R}>1.1}$$のパラメータは「0」件です。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

平滑化後の「状態」smoothed_state、状態のノイズ sigma_trend、観測ノイズ sigma_obs の事後分布の要約統計量です。
### 推論データの要約統計情報の表示(一部)
var_names = ['smoothed_state', 'sigma_trend', 'sigma_obs']
pm.summary(idata_ss1, hdi_prob=0.95, var_names=var_names)【実行結果】
期間数が多いため抜粋となりました(汗)

トレースプロットを確認しましょう。
PyMCモデル定義で追加した4つのパラメータを見ます。
### トレースプロットの表示
pm.plot_trace(idata_ss1, combined=True, var_names=ss_model1.param_names,
figsize=(10, 8))
plt.tight_layout();【実行結果】
収束している感じがします。
P0は一様分布の0~1の区間を幅広く漂っており、何となく良い結果とは言えない予感がします。

⑤ 状態smoothed_stateを描画
状態smoothed_stateの事後平均値と80%HDI・50%HDI区間を描画してみます。
正直なところ、このsmoothed_stateが状態「mu」を示しているのか不安です。
繰り返し利用するので描画関数を定義します。
### smooth_stateの事後分布の平均値、50%・80%HDI区間の描画関数の定義
def ss_state_plot(idata):
## 事後平均・80%HDI・50%HDIの算出
tmp = idata.posterior
mean = (tmp.smoothed_state.stack(sample=('chain', 'draw'))
.squeeze().mean(axis=1).data)
hdi80 = az.hdi(tmp, hdi_prob=0.80).smoothed_state.squeeze().data
hdi50 = az.hdi(tmp, hdi_prob=0.50).smoothed_state.squeeze().data
## 描画
fig, ax = plt.subplots(figsize=(10, 3))
# 100日の垂直線の描画
ax.axvline(100, color='black', lw=0.8, ls='--')
# 観測値の描画
ax.scatter(df_ss['Time'], df_ss['y'], color='blue', s=8, label='観測値')
## 観測期間
# 事後平均の描画
ax.plot(df_ss['Time'], mean, color='tab:blue', label='事後平均')
# 80%HDI区間の描画
ax.fill_between(df_ss['Time'], hdi80[:, 0], hdi80[:, 1], color='tab:blue',
alpha=0.15, label='HDI 80%')
# 50%HDI区間の描画
ax.fill_between(df_ss['Time'], hdi50[:, 0], hdi50[:, 1], color='tab:blue',
alpha=0.4, label='HDI 50%')
# 修飾
ax.set(xlabel='Time', ylabel='$state$ EAP')
ax.grid(lw=0.3)
ax.legend(bbox_to_anchor=(1.18, 1))
plt.show()描画します。
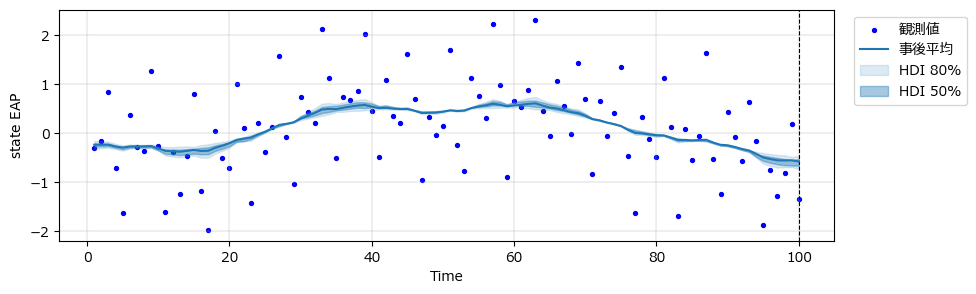
### smoothed_stateの事後分布のプロット ★図4.11(ただし20期先予測なし)に相当
ss_state_plot(idata_ss1)【実行結果】
HDI区間の幅がキュッと狭くなりました。
状態空間モデルの実力値なのか、私の実装ミスなのか、、、。
⑥ 状態変数の事後分布と将来予測
sample_conditional_posterior()を用いて、状態変数の事後分布のサンプリングを実行します。
### 状態変数の事後予測のサンプリングの実行
post_ss1 = ss_model1.sample_conditional_posterior(idata_ss1, random_seed=1234)【実行結果】

続いて将来予測を実施します。
### 将来予測のサンプリングの実行
# 初期値設定:予測期間
n_periods = 21
# 将来予測のサンプリングの実行
forecasts_ss1 = ss_model1.forecast(idata_ss1, start=df_ss.index[-1],
periods=n_periods, random_seed=1234)【実行結果】

目的変数「y」の事後分布および将来予測データを描画します。
恒例の描画関数の定義です。
### 描画関数の定義
def ss_forecast_plot(post, forecast):
### 事後予測・将来予測の平均・HDIの算出
# 事後予測
mean_post = (post.stack(sample=('chain', 'draw'))
.smoothed_posterior_observed.squeeze().mean(axis=1))
hdi_post80 = (az.hdi(post, hdi_prob=0.80).smoothed_posterior_observed
.squeeze())
hdi_post50 = (az.hdi(post, hdi_prob=0.50).smoothed_posterior_observed
.squeeze())
# 将来予測
mean_fore = (forecast.stack(sample=('chain', 'draw'))
.forecast_observed.squeeze().mean(axis=1))
hdi_fore80 = az.hdi(forecast, hdi_prob=0.80).forecast_observed.squeeze()
hdi_fore50 = az.hdi(forecast, hdi_prob=0.50).forecast_observed.squeeze()
### 描画
fig, ax = plt.subplots(figsize=(10, 3))
## 観測値の描画
ax.scatter(df_ss['Time'], df_ss['y'], color='blue', s=8, label='観測値')
## 事後予測の描画
# 事後平均の描画
ax.plot(df_ss['Time'], mean_post, color='tab:blue', label='事後平均')
# 80%HDI区間の描画
ax.fill_between(df_ss['Time'], hdi_post80[:, 0], hdi_post80[:, 1],
color='tab:blue', alpha=0.15, label='HDI 80%')
# 50%HDI区間の描画
ax.fill_between(df_ss['Time'], hdi_post50[:, 0], hdi_post50[:, 1],
color='tab:blue', alpha=0.4, label='HDI 50%')
## 将来予測の描画
# x軸の作成
x_add = list(range(df_ss['Time'].max(), df_ss['Time'].max()+21))
# 平均の描画
ax.plot(x_add, mean_fore, color='red', label='将来予測')
# 80%HDI区間の描画
ax.fill_between(x_add, hdi_fore80[:, 0], hdi_fore80[:, 1], color='tomato',
alpha=0.15, label='HDI 80%')
# 50%HDI区間の描画
ax.fill_between(x_add, hdi_fore50[:, 0], hdi_fore50[:, 1], color='tomato',
alpha=0.4, label='HDI 50%')
## 修飾
ax.set(xlabel='Time', ylabel='y, EAP')
ax.grid()
ax.legend(bbox_to_anchor=(1.18, 1))
plt.show()描画します。
### yの事後予測・将来予測のプロット
ss_forecast_plot(post_ss1, forecasts_ss1)【実行結果】
ランダムウォークやAR(1)を用いたモデルと大差ない感じです。


レベルの変化に加えて傾きの変化も考慮したローカル線形トレンドモデル
$${\mu_t}$$にトレンド$${v_t}$$が加わる「ローカル線形トレンドモデル」に挑戦します!
トレンドは「傾き」・「ドリフト」とも呼ばれるそうです。
$$
\begin{align*}
\mu_t &= \mu_{t-1} + v_t + \varepsilon_t, \quad \varepsilon_t \sim \text{Normal}\ (0,\ \sigma^2_{\varepsilon}) \cdots システムモデル※\\
v_t &= v_{t-1} + \zeta_t, \quad \zeta_t \sim \text{Normal}\ (0,\ \sigma^2_{\zeta}) \cdots システムモデル※\\
y_t &= \mu_t + \xi_t, \quad \xi_t \sim \text{Normal}\ (0,\ \sigma^2_{\xi}) \cdots 観測モデル\\
\end{align*}
$$
$${\mu_t}$$はレベルに関するシステムモデル、$${v_t}$$はトレンドに関するシステムモデルです。
ギリシア文字の読みは、$${\varepsilon}$$は「イプシロン」、$${\zeta}$$は「ゼータ」、$${\xi}$$は「クサイ」です。

このローカル線形トレンドモデルでは、次の2つのモデルを試みます。
システムモデル(状態方程式)にガウスランダムウォークを適用
状態空間モデル専用のモデルを適用
PyMCのARモデルは(おそらく・私の知るところでは)、傾き・トレンド項を含められないので、断念しました。
1.ガウスランダムウォーク
① モデルの定義
状態「mu」 とトレンド「v」に pm.GaussianRandomWalk()を用います。
「mu」の引数で「mu=v」と指定することで、「v」が入れ子の関係になり、「v」の形状(shape)が全期間の120か月から1か月短い「119」か月になります。
### モデルの定義
# モデルの定義
with pm.Model() as model_rw2:
### データ関連定義
# coordの定義
model_rw2.add_coord('data', values=idx_fore, mutable=True)
# # dataの定義 ※欠損値を含んだデータは定義できない
# y = pm.ConstantData('y', value=y_fore, dims='data')
### 事前分布
sigmaS = pm.HalfCauchy('sigmaS', beta=5) # レベルの標準偏差
sigmaV = pm.HalfCauchy('sigmaV', beta=5) # トレンドの標準偏差
sigmaO = pm.HalfCauchy('sigmaO', beta=5) # 観測モデルの標準偏差
### muの計算
# v:トレンド(ドリフト)
init_dist_v = pm.Normal.dist(mu=0, sigma=100)
v = pm.GaussianRandomWalk('v', sigma=sigmaV, init_dist=init_dist_v,
shape=len(y_fore)-1) # 注意:shapeはmuのshape-1
# dims='data')
# mu:レベル
init_dist_mu = pm.Normal.dist(mu=0, sigma=100)
mu = pm.GaussianRandomWalk('mu', mu=v, sigma=sigmaS, init_dist=init_dist_mu,
dims='data')
### 尤度
likelihood = pm.Normal('likelihood', mu=mu, sigma=sigmaO, observed=y_fore,
dims='data')【実行結果】出力なし
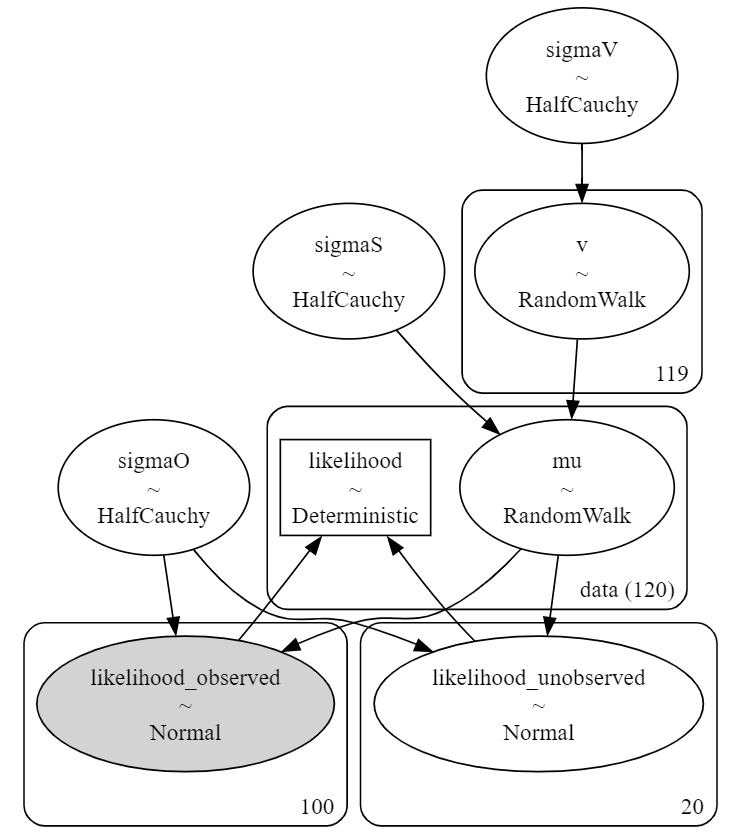
② モデルの可視化
# モデルの可視化
pm.model_to_graphviz(model_rw2)【実行結果】
トレンド項が一層増えた様子がよく分かります。
③ 事後分布からのサンプリング
MCMCを実行します。
データに欠損値を含むため、PyMC標準のサンプラーを使用します。
実行時間はおよそ33分30秒でした。
### 事後分布からのサンプリング ※欠損値を含む→PyMC標準のサンプラー 33分30秒
with model_rw2:
idata_rw2 = pm.sample(draws=2000, tune=2000, chains=4, target_accept=0.9,
random_seed=1234)【実行結果】

④ サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.1}$$としています。
### r_hat>1.1の確認
# 設定
idata_in = idata_rw2 # idata名
threshold = 1.1 # しきい値
# しきい値を超えるR_hatの個数を表示
(az.rhat(idata_in) > threshold).sum().data_vars【実行結果】
sigmaS(muのノイズ)とsigmaV(トレンドのノイズ)が$${\hat{R}>1.1}$$となり、収束しませんでした(汗)


この2つのパラメータの要約統計情報を確認します。
### sigmaS、sigmaVの要約統計情報の表示
pm.summary(idata_rw2, hdi_prob=0.95, var_names=['sigmaS', 'sigmaV'])【実行結果】
確かにr_hatは1.1を超えています。残念。。。

【作戦会議】
収束していない状態のデータを使うので、以降のコード・実行結果は、データ内容の吟味は避けて、コード実装の確認用の目的で描きます。
欠損値を含まない観測値データを用いたモデリングでは、$${\hat{R} \leq 1.1}$$となり、収束します。
では続行します。
パラメータ等の事後分布の要約統計量です。
### 推論データの要約統計情報の表示
pm.summary(idata_rw2, hdi_prob=0.95)【実行結果】
一部抜粋となります。

トレースプロットを確認しましょう。
### トレースプロットの表示
pm.plot_trace(idata_rw2, combined=True, figsize=(10, 10))
plt.tight_layout();【実行結果】
発散のバーコードが見られます。

⑤ 真の状態$${\boldsymbol{\mu}}$$を描画
状態「mu」の事後平均値と80%HDI・50%HDI区間を描画します。
テキストの図4.11中に相当します。
### muの事後分布のプロット ★図4.11に相当
plot_mu_posterior(idata_rw2)【実行結果】
ローカルレベルモデルよりもHDI区間の幅が狭くなっている感じです。
赤い将来予測は下降トレンドを示しているようです。

⑥ 観測される$${\boldsymbol{y}}$$の事後予測を描画
目的変数「y」の事後予測を行って描画します。
### 事後予測のサンプリングの実施
with model_rw2:
idata_rw2.extend(pm.sample_posterior_predictive(idata_rw2))【処理結果】

「y」の事後予測サンプリングデータを描画します。
### yの事後予測のプロット
plot_posterior_pred(idata_rw2)【実行結果】


2.状態空間モデル
① モデルの定義
2段階でモデルを定義します。
1段階目は状態空間モデルの定義です。
### 状態空間モデルの定義
# レベル・トレンド成分の定義
# μt = μt-1 + vt+ εt, εt ~ Normal(0, σε²)
# vt = vt-1 + ζt, ζt ~ Normal(0, σζ²)
trend = st.LevelTrendComponent(order=2, innovations_order=2)
# 測定ノイズの定義 分散パラメータσξ²
error = st.MeasurementError(name='obs')
# レベル・トレンド成分と観測ノイズで状態空間モデルを構築
ss_model2 = (trend + error).build(name='local2')【補足】
■ LevelTrendComponent
時系列変数が2個あること(order=2)、状態のノイズが2個であること(innovations_order=2)のようです。
【実行結果】
PyMCモデルの定義で設定の必要な「パラメータ」を指示してくれます。
指示通りのパラメータ名を用いて、形状、制約(正の数など)、次元を設定します。

では2段階目のPyMCモデルを定義しましょう。
### PyMCモデルの定義
with pm.Model(coords=ss_model2.coords) as model_ss2:
## パラメータの事前分布
# 初期値の標準偏差
P0_diag = pm.Gamma('P0_diag', alpha=2, beta=1, dims=['state'])
P0 = pm.Deterministic('P0', pt.diag(P0_diag), dims=['state', 'state_aux'])
# レベル・トレンド成分の初期値
initial_trend = pm.Normal('initial_trend', mu=0, sigma=100,
dims=['trend_state'])
# 状態変数の標準偏差
sigma_trend = pm.HalfCauchy('sigma_trend', beta=5, dims=['trend_shock'])
sigma_obs = pm.HalfCauchy('sigma_obs', beta=5)
## 状態空間モデルの計算グラフ構築
ss_model2.build_statespace_graph(data=df_ss['y'], mode='JAX')【実行結果】出力なし
【補足】
P0、initial_trend、sigma_trend、sigma_obsは状態空間モデルの定義時に指示のあったパラメータです。
P0:(おそらく)何かの初期値の標準偏差に使われる模様です(推測)。
適切な設定値(お作法)がわからないので、ひとまずガンマ分布にして、「pt.diag()」で2×2の対角行列にしています(していると思っています)。その他のパラメータはローカルレベルモデルと同様の考え方で設定しました。
② モデルの表示・可視化
### モデルの表示()
model_ss2.__getstate__()【実行結果】

可視化します。
# モデルの可視化
pm.model_to_graphviz(model_ss2)【実行結果】
潜水艦みたいになりました。
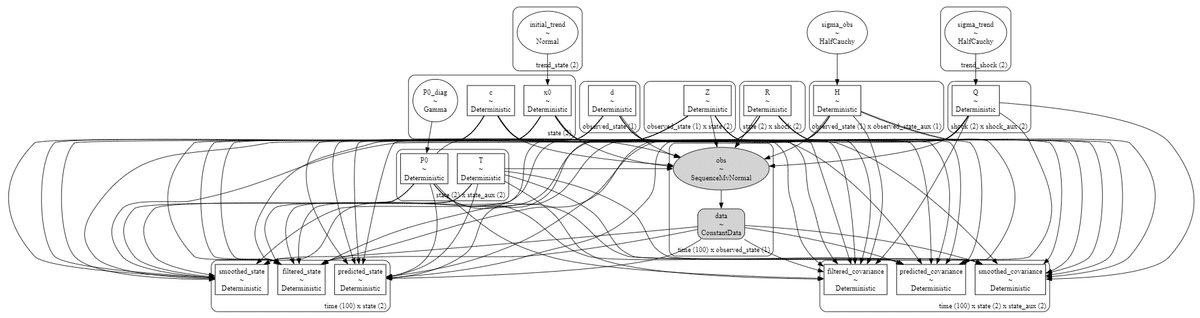
③ 事後分布からのサンプリング
ここからは通常のPyMCモデルと同様の処理になります。
ではMCMCを実行しましょう!
NUTSサンプラーにnumpyroを使用するので爆速です(のはずです)。
実行時間は約1分15秒でした。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 1分15秒
with model_ss2:
idata_ss2 = pm.sample(draws=2000, tune=2000, chains=4, target_accept=0.9,
nuts_sampler='numpyro', random_seed=1234)【実行結果】

④ サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.1}$$としています。
### r_hat>1.1の確認
# 設定
idata_in = idata_ss2 # idata名
threshold = 1.1 # しきい値
# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in).to_dataframe() > threshold).sum())【実行結果】
$${\hat{R}>1.1}$$のパラメータは「0」件です。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

平滑化後の「状態」smoothed_state、状態のノイズ sigma_trend、観測ノイズ sigma_obs の事後分布の要約統計量です。
### 推論データの要約統計情報の表示
var_names = ['smoothed_state', 'sigma_trend', 'sigma_obs']
pm.summary(idata_ss2, hdi_prob=0.95, var_names=var_names)【実行結果】
期間数が多いため抜粋となりました(汗)

トレースプロットを確認しましょう。
PyMCモデル定義で追加した4つのパラメータを見ます。
### トレースプロットの表示
pm.plot_trace(idata_ss2, combined=True, var_names=ss_model2.param_names,
figsize=(10, 8))
plt.tight_layout();【実行結果】
収束している感じがします。
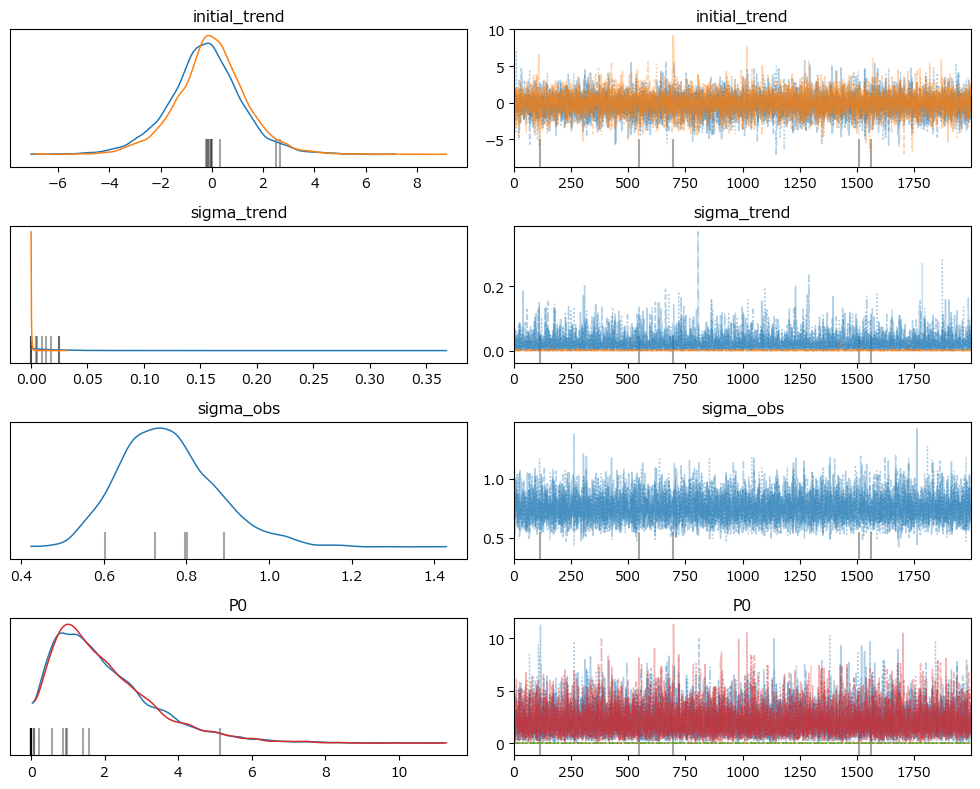
⑤ 状態smoothed_stateを描画
状態smoothed_stateの事後平均値と80%HDI・50%HDI区間を描画してみます。
正直なところ、このsmoothed_stateが状態「mu」を示しているのか不安です。
smoothed_stateデータの次元に「state」が加わったので、改めて描画関数を定義します。
### smooth_stateの事後分布の平均値、50%・80%HDI区間の描画関数2の定義
def ss_state_plot2(idata):
## 事後平均・80%HDI・50%HDIの算出
mean = (idata.posterior.smoothed_state.stack(sample=('chain', 'draw'))
.sum(axis=1).mean(axis=1))
tmp = (idata.posterior.smoothed_state.stack(sample=('chain', 'draw'))
.sum(axis=1).data.T)
hdi80 = az.hdi(tmp, hdi_prob=0.80)
hdi50 = az.hdi(tmp, hdi_prob=0.50)
## 描画
fig, ax = plt.subplots(figsize=(10, 3))
# 100日の垂直線の描画
ax.axvline(100, color='black', lw=0.8, ls='--')
# 観測値の描画
ax.scatter(df_ss['Time'], df_ss['y'], color='blue', s=8, label='観測値')
## 観測期間
# 事後平均の描画
ax.plot(df_ss['Time'], mean, color='tab:blue',
label='事後平均')
# 80%HDI区間の描画
ax.fill_between(df_ss['Time'], hdi80[:, 0], hdi80[:, 1],
color='tab:blue', alpha=0.15, label='HDI 80%')
# 50%HDI区間の描画
ax.fill_between(df_ss['Time'], hdi50[:, 0], hdi50[:, 1],
color='tab:blue', alpha=0.4, label='HDI 50%')
# 修飾
ax.set(xlabel='Time', ylabel='$state$ EAP')
ax.grid(lw=0.3)
ax.legend(bbox_to_anchor=(1.18, 1))
plt.show()描画します。
### smoothed_stateの事後分布のプロット ★図4.11(ただし20期先予測なし)に相当
ss_state_plot2(idata_ss2)【実行結果】
ローカルレベルモデルよりもHDI区間の幅が狭くなりました。
トレンドを考慮したからでしょうか。

⑥ 状態変数の事後分布と将来予測
sample_conditional_posterior()を用いて、状態変数の事後分布のサンプリングを実行します。
### 状態変数の事後予測のサンプリングの実行
post_ss2 = ss_model2.sample_conditional_posterior(idata_ss2, random_seed=1234)【実行結果】

続いて将来予測を実施します。
### 将来予測のサンプリングの実行
# 初期値設定:予測期間
n_periods = 21
# 将来予測のサンプリングの実行
forecasts_ss2 = ss_model2.forecast(idata_ss2, start=df_ss.index[-1],
periods=n_periods, random_seed=1234)【実行結果】

目的変数「y」の事後分布および将来予測データを描画します。
### yの事後予測・将来予測のプロット
ss_forecast_plot(post_ss2, forecasts_ss2)【実行結果】
赤い将来予測部分は下降トレンドを示しており、また、HDI区間の幅が、期間が大きくなるにつれて広くなっています。
下のローカルレベルモデルの描画と比べてみましょう。

(参考:ローカルレベルモデルの y の事後分布・将来予測の描画)


季節成分を考慮したローカルレベルモデル
目的変数$${y}$$に「周期$${S}$$の季節成分を表す$${\gamma}$$」を加えたローカルレベルモデルです。
$$
\begin{align*}
\mu_t &= \mu_{t-1} + \varepsilon_t, \quad \varepsilon_t \sim \text{Normal}\ (0,\ \sigma^2_{\varepsilon}) \cdots システムモデル※\\
\gamma_t &= -\sum^{S-1}_{j=1} \gamma_{t-j} + \omega_t, \quad \omega_t \sim \text{Normal}\ (0,\ \sigma^2_{\omega}) \cdots システムモデル※\\
y_t &= \mu_t + \gamma_t + \xi_t, \quad \xi_t \sim \text{Normal}\ (0,\ \sigma^2_{\xi}) \cdots 観測モデル\\
\end{align*}
$$
$${\mu_t}$$はレベルに関するシステムモデル、$${\gamma_t}$$は周期$${S}$$の季節成分に関するシステムモデルです。
ギリシア文字の読みは、$${\varepsilon}$$は「イプシロン」、$${\omega}$$は「オメガ」、$${\xi}$$は「クサイ」です。

このローカルレベルモデルでは、次の2つのモデルを試みます。
システムモデル(状態方程式)に自己回帰モデルAR(1)を適用
状態空間モデル専用のモデルを適用
今回のモデルの季節成分は11次の自己回帰過程ですので、PyMCのGaussianRandomWalkモデルは(おそらく・私の知るところでは)、適用できないです。
1.自己回帰AR(1)
① モデルの定義
状態「mu」 に相当するレベル(・トレンド)成分「trend」と、季節成分「season」に pm.AR()を用います。
なお、3つのノイズの事前分布はテキストと異なっています。
テキストでは事前分布を明示的に指定していないので、おそらく範囲の広い一様分布を仮定していると思われます。
この記事のモデルでは、ローカルレベルモデル、ローカル線形トレンドモデルと同じ事前分布にしました。
### モデルの定義
# ARパラメータの設定
period = 12 # 季節成分の周期
order = period - 1 # ARの次数
rhos = np.ones(order) * -1 # ARのρパラメータ
# モデルの定義
with pm.Model() as model_ar3:
### データ関連定義
# coordの定義
model_ar3.add_coord('data', values=idx_fore, mutable=True)
# # dataの定義 ※欠損値を含んだデータは定義できない
# y = pm.ConstantData('y', value=y_fore, dims='data')
### 事前分布
# テキストは事前分布を定義していない(おそらく一様分布)
# 本モデルは他のモデルと平仄をとって半コーシー分布を仮定した
sigmaW = pm.HalfCauchy('sigmaW', beta=5) # システムノイズ
sigmaS = pm.HalfCauchy('sigmaS', beta=5) # 季節調整項の合計のばらつき
sigmaO = pm.HalfCauchy('sigmaO', beta=5) # 観測ノイズ
### レベル・トレンド成分
init_dist_trend = pm.Normal.dist(mu=0, sigma=100)
trend = pm.AR('trend', rho=1, sigma=sigmaW, constant=False,
init_dist=init_dist_trend, ar_order=1, dims='data')
### 季節成分
init_dist_season = pm.Normal.dist(mu=0, sigma=100)
season = pm.AR('season', rho=rhos, sigma=sigmaS, constant=False,
init_dist=init_dist_season, ar_order=order, dims='data')
### 尤度
likelihood = pm.Normal('likelihood', mu=trend+season, sigma=sigmaO,
observed=y_fore, dims='data')
### 計算値
mu = pm.Deterministic('mu', trend + season)【実行結果】出力なし
【補足】
「trend」の記述はローカルレベルモデルと同じです。
季節成分は周期12($${S=12}$$)を設定します。
「season」の記述は、次数orderが$${S-1=12-1=11}$$、自己回帰係数 rhoが $${\rho_1, \cdots, \rho_{11}=-1}$$です。また mu を描画する目的で、計算値「mu」を設定しました。
② モデルの可視化
# モデルの可視化
pm.model_to_graphviz(model_ar3)【実行結果】
trendとseasonの名称、なかなか良きです。

③ 事後分布からのサンプリング
MCMCを実行します。
データに欠損値を含むため、PyMC標準のサンプラーを使用します。
実行時間はおよそ26分30秒でした。
### 事後分布からのサンプリング ※欠損値を含む→PyMC標準のサンプラー 26分30秒
with model_ar3:
idata_ar3 = pm.sample(draws=2000, tune=2000, chains=4, target_accept=0.9,
random_seed=1234)【実行結果】

④ サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.1}$$としています。
### r_hat>1.1の確認
# 設定
idata_in = idata_ar3 # idata名
threshold = 1.1 # しきい値
# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in) > threshold).sum().data_vars)【実行結果】
$${\hat{R}>1.1}$$のパラメータは「0」件です。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

パラメータ等の事後分布の要約統計量です。
### 推論データの要約統計情報の表示
pm.summary(idata_ar3, hdi_prob=0.95)【実行結果】
一部抜粋となります。

トレースプロットを確認しましょう。
### トレースプロットの表示
pm.plot_trace(idata_ar3, combined=True, figsize=(10, 12))
plt.tight_layout();【実行結果】
発散のバーコードが見られます。
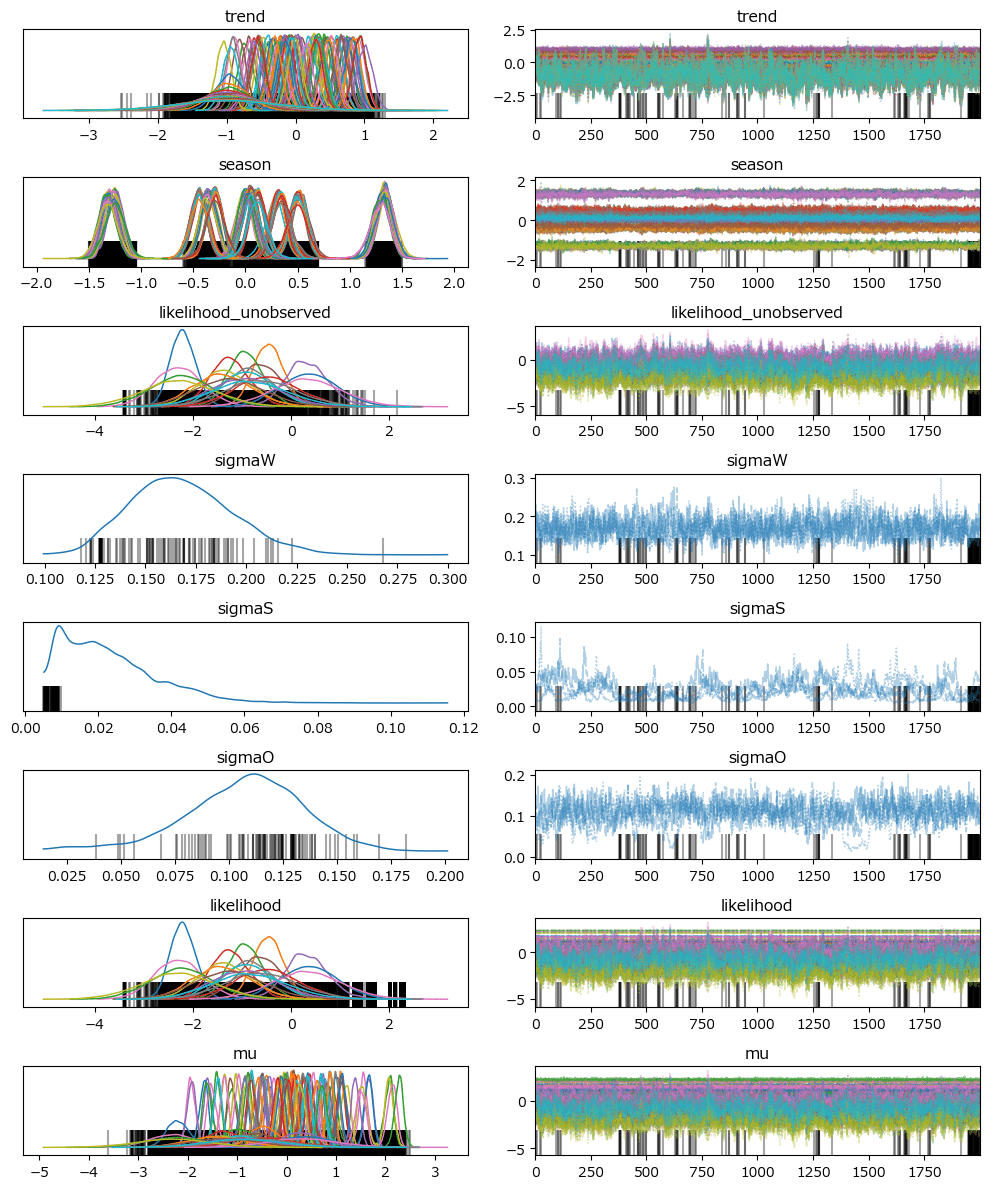
⑤ 真の状態$${\boldsymbol{\mu}}$$を描画
状態「mu」の事後平均値と80%HDI・50%HDI区間を描画します。
テキストの図4.11下に相当します。
### muの事後分布のプロット ★図4.11に相当
plot_mu_posterior(idata_ar3)【実行結果】
観測値にピタッとはまった結果になりました。
周期12の季節成分を考慮した結果、観測期間はHDI区間の幅がほぼ無く、赤色の予測期間も幅が狭まっています。
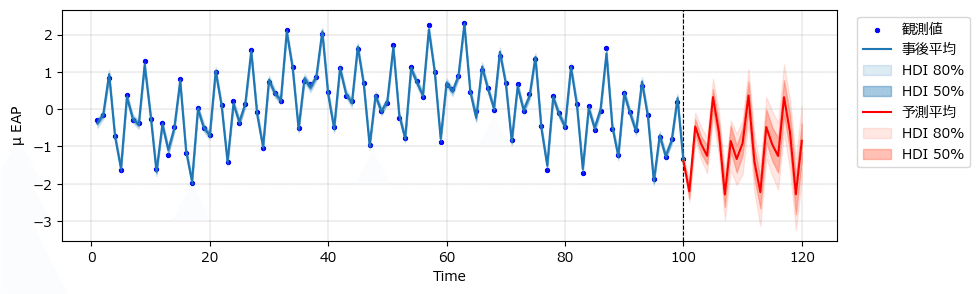
レベル(・トレンド)成分の平均値と、レベル(・トレンド)成分+季節成分の平均値をおなじ図内に描画しましょう。
### トレンド成分, 季節成分の推論データをプロット
## 描画データの準備
# x軸:期間1~120
x = idx_fore + 1
# trendデータ
y1 = idata_ar3.posterior.trend.stack(sample=('chain', 'draw')).mean(axis=1).data
# trend+seasonデータ
y2 = idata_ar3.posterior.trend.stack(sample=('chain', 'draw')).mean(axis=1).data \
+ idata_ar3.posterior.season.stack(sample=('chain', 'draw')).mean(axis=1).data
## 描画
plt.figure(figsize=(10, 4))
# trendデータの描画
plt.plot(x, y1, color='tab:orange', label='trend')
# trend+seasonデータの描画
plt.plot(x, y2, color='tab:blue', label='trend+season')
# 観測データの描画
plt.plot(df_ss['Time'], df_ss['y'], ls=':', color='tab:red',
label='観測データ')
# 期間100の垂直線の描画
plt.axvline(100, color='black', lw=0.5, ls='--')
# 修飾
plt.xlabel('Time')
plt.legend()
plt.show()【実行結果】
100か月以後の将来期間では、レベル(・トレンド)成分はほぼ水平になっており、季節成分が6か月の周期で上下している様子がよく分かります。

⑥ 観測される$${\boldsymbol{y}}$$の事後予測を描画
目的変数「y」の事後予測を行って描画します。
### 事後予測のサンプリングの実施
with model_ar3:
idata_ar3.extend(pm.sample_posterior_predictive(idata_ar3))【処理結果】

「y」の事後予測サンプリングデータを描画します。
### yの事後予測のプロット
plot_posterior_pred(idata_ar3)【実行結果】
目的変数 y の事後分布・将来予測値もピタッとはまった結果になりました。
下の図は(収束していないので申し訳ないですが)、ガウスランダムウォークを用いたローカル線形トレンドモデルのときの同じ描画です。

(参考:ローカル線形トレンドモデルの y の事後分布・将来予測の描画)


2.状態空間モデル
① モデルの定義
2段階でモデルを定義します。
1段階目は状態空間モデルの定義です。
### 状態空間モデルの定義
# レベル・トレンド成分の定義
# μt = μt-1 + εt, εt ~ Normal(0, σε²)
trend = st.LevelTrendComponent(order=1, innovations_order=1)
# 季節成分の定義
# γt = -Σ^{S-1}_{j=1} (γt-1 + ωt), ωt ~ Normal(0, σω²)
season = st.FrequencySeasonality(season_length=12, innovations=True, name='season')
# 観測ノイズの定義 観測誤差ξt
error = st.MeasurementError(name='obs')
# レベル・トレンド成分+季節成分+観測ノイズで状態空間モデルを構築
ss_model3 = (trend + season + error).build(name='local3')【補足】
■ FrequencySeasonality
季節成分を「頻度」(Frequency)で指定するコンポーネントです。
周期 season_length=12、ノイズあり innovations=True です。
【注記】
季節成分のコンポーネントにはもう1つ「TimeSeasonality」があります。
こちらの方が柔軟性の高い設定ができるようなのですが、このモデル構築では何故か(原因不明なのは私の限界です(泣))エラーになり、利用を断念しました、、、。
【実行結果】
PyMCモデルの定義で設定の必要な「パラメータ」を指示してくれます。
指示通りのパラメータ名を用いて、形状、制約(正の数など)、次元を設定します。
季節成分関連のパラメータが増えました。

では2段階目のPyMCモデルを定義しましょう。
### PyMCモデルの定義
with pm.Model(coords=ss_model3.coords) as model_ss3:
## パラメータの事前分布
# 初期値の標準偏差
P0_diag = pm.Gamma('P0_diag', alpha=2, beta=1, dims=['state'])
P0 = pm.Deterministic('P0', pt.diag(P0_diag), dims=['state', 'state_aux'])
# レベル・トレンド成分の初期値
initial_trend = pm.Normal('initial_trend', mu=0, sigma=100,
dims=['trend_state'])
# 季節成分の係数の初期値
season = pm.Normal('season', mu=0, sigma=100, dims=['season_initial_state'])
# 状態変数の標準偏差
sigma_trend = pm.HalfCauchy('sigma_trend', beta=5, dims=['trend_shock'])
sigma_season = pm.HalfCauchy('sigma_season', beta=5)
sigma_obs = pm.HalfCauchy('sigma_obs', beta=5)
## 状態空間モデルの計算グラフ構築
ss_model3.build_statespace_graph(data=df_ss['y'], mode='JAX')【実行結果】出力なし
【補足】
P0、initial_trend、sigma_trend、sigma_obsは状態空間モデルの定義時に指示のあったパラメータです。
P0:(おそらく)何かの初期値の標準偏差に使われる模様です(推測)。
適切な設定値(お作法)がわからないので、ひとまずガンマ分布にして、「pt.diag()」で2×2の対角行列にしています(していると思っています)。その他のパラメータはローカルレベルモデルと同様の考え方で設定しました。
② モデルの表示・可視化
### モデルの表示()
model_ss3.__getstate__()【実行結果】

可視化します。
# モデルの可視化
pm.model_to_graphviz(model_ss3)【実行結果】
巨大な潜水艦みたいになりました。

③ 事後分布からのサンプリング
ここからは通常のPyMCモデルと同様の処理になります。
ではMCMCを実行しましょう!
NUTSサンプラーにnumpyroを使用するので爆速です(のはずです)。
実行時間は約44分30秒でした。
なぜこんなに時間がかかったのか不明です(???)
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 44分30秒
with model_ss3:
idata_ss3 = pm.sample(draws=2000, tune=2000, chains=4, target_accept=0.9,
nuts_sampler='numpyro', random_seed=1234)【実行結果】
④ サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認はテキストにならって$${\hat{R} \leq 1.1}$$としています。
### r_hat>1.1の確認
# 設定
idata_in = idata_ss3 # idata名
threshold = 1.1 # しきい値
# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in).to_dataframe() > threshold).sum())【実行結果】
$${\hat{R}>1.1}$$のパラメータは「0」件です。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

平滑化後の「状態」smoothed_state、状態のノイズ sigma_trend、観測ノイズ sigma_obs の事後分布の要約統計量です。
### 推論データの要約統計情報の表示
var_names = ['smoothed_state', 'sigma_trend', 'sigma_obs']
pm.summary(idata_ss3, hdi_prob=0.95, var_names=var_names)【実行結果】
1302行!
抜粋となりました(汗)

トレースプロットを確認しましょう。
PyMCモデル定義で追加した4つのパラメータを見ます。
### トレースプロットの表示
pm.plot_trace(idata_ss3, combined=True, var_names=ss_model3.param_names,
figsize=(10, 12))
plt.tight_layout();【実行結果】
収束している感じがします。
発散を示すバーコードが気になります。

⑤ 状態smoothed_stateを描画
状態smoothed_stateの事後平均値と80%HDI・50%HDI区間を描画してみます。
正直なところ、このsmoothed_stateが状態「mu」を示しているのか不安です。
### smoothed_stateの事後分布のプロット ★図4.11(ただし20期先予測なし)に相当
ss_state_plot2(idata_ss3)【実行結果】
事後平均とそのHDI区間は「線」のように細いです!
状態「state」は観測ノイズを含まないため、観測値「y」とは乖離するのでしょう。

⑥ 状態変数の事後分布と将来予測
sample_conditional_posterior()を用いて、状態変数の事後分布のサンプリングを実行します。
### 状態変数の事後予測のサンプリングの実行
post_ss3 = ss_model3.sample_conditional_posterior(idata_ss3, random_seed=1234)【実行結果】

続いて将来予測を実施します。
### 将来予測のサンプリングの実行
# 初期値設定:予測期間
n_periods = 21
# 将来予測のサンプリングの実行
forecasts_ss3 = ss_model3.forecast(idata_ss3, start=df_ss.index[-1],
periods=n_periods, random_seed=1234)【実行結果】

目的変数「y」の事後分布および将来予測データを描画します。
### yの事後予測・将来予測のプロット
ss_forecast_plot(post_ss3, forecasts_ss3)【実行結果】
季節成分の威力はすごいですね!
下の2つのモデルの描画と比べてみましょう。
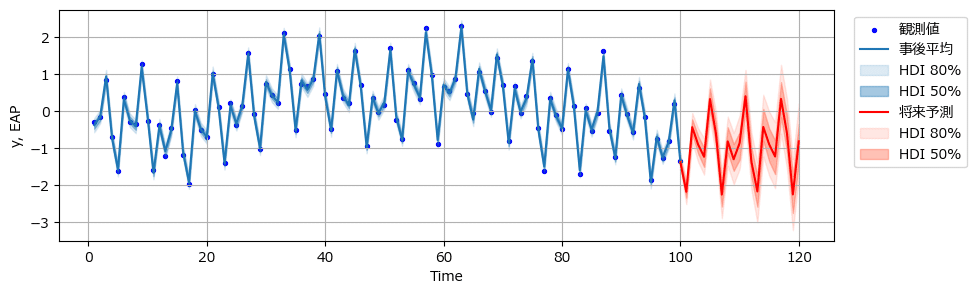
(参考:ローカル線形トレンドモデルの y の事後分布・将来予測の描画)

(参考:ローカルレベルモデルの y の事後分布・将来予測の描画)

以上で終了です。
お疲れ様でした。

まとめ
レベル成分、トレンド成分、季節成分で構成する状態空間モデルを学びました。
レベル成分とトレンド成分は階層(入れ子)になるのでガウスランダムウォークで表現できることが分かりました。
季節成分は「周期-1」の次数をもつ自己回帰モデルで表現できることが分かりました。
将来予測のための欠損値を含むデータを用いて、ガウスランダムウォークや自己回帰モデルを構築する際には、次の点を考慮するのが良さそうです。
PyMC標準のサンプラーを用いるのでMCMCに時間がかかる(回避策はあるかもですが、現時点で把握していません)。
収束しない可能性が高まる。
「pymc_experimental.statespace」の状態空間モデルに慣れれば、ガウスランダムウォークや自己回帰モデルを用いるモデルに比べて、いっそう柔軟なモデリングができそうです。
そうそう、推論データ(idata)を保存いたしましょう。
pickle形式で保存します。
### idataの保存 pickle
import pickle
file = r'ch04_02_idata_rw1.pkl'
with open(file, 'wb') as f:
pickle.dump(idata_rw1, f)
file = r'ch04_02_idata_ar1.pkl'
with open(file, 'wb') as f:
pickle.dump(idata_ar1, f)
file = r'ch04_02_idata_ss1.pkl'
with open(file, 'wb') as f:
pickle.dump(idata_ss1, f)
file = r'ch04_02_idata_rw2.pkl'
with open(file, 'wb') as f:
pickle.dump(idata_rw2, f)
file = r'ch04_02_idata_ss2.pkl'
with open(file, 'wb') as f:
pickle.dump(idata_ss2, f)
file = r'ch04_02_idata_ar3.pkl'
with open(file, 'wb') as f:
pickle.dump(idata_ar3, f)
file = r'ch04_02_idata_ss3.pkl'
with open(file, 'wb') as f:
pickle.dump(idata_ss3, f)読み込みコードは次のとおりです。
「file」のパス&ファイル名と「idata_rw1_load」を適宜変更してお使い下さい。
### idataの読み込み(例)
file = r'./save/ch04_02_idata_rw1.pkl'
with open(file, 'rb') as f:
idata_rw1_load = pickle.load(f)
第4章 その3 へ続く
■次回の取り組みテーマ
引き続き、状態空間モデルを学びます。
1.パネルデータの分析
・ランダム切片モデル
・潜在成長曲線モデル
2.多変量時系列の解析
・Correlated Random Walk (CRW) モデル
次の記事
前の記事
目次
ブログの紹介
note で4つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
2.実験!たのしいベイズモデリングをPyMC Ver.5で
書籍「たのしいベイズモデリング」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learn と PyTorch の教科書です。
よかったらぜひ、お試しくださいませ。
4.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Python のコラムを不定期に綴っています。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
最後までお読みいただきまして、ありがとうございました。
