
「数値シミュレーションで読み解く統計のしくみ」をPythonで写経 ~ 第3章3.4「任意の相関係数を持つ変数が従う確率分布」
第3章「乱数生成シミュレーションの基礎」
書籍の著者 小杉考司 先生、紀ノ定保礼 先生、清水裕士 先生
この記事は、テキスト「数値シミュレーションで読み解く統計のしくみ」第3章「乱数生成シミュレーションの基礎」3.4節「任意の相関係数を持つ変数が従う確率分布」の Python写経活動 を取り扱います。
今回は相関係数と多変量正規分布の結びつきを確認します。
R の基本的なプログラム記法はざっくり Python の記法と近いです。
コードの文字の細部をなぞって、R と Python の両方に接近してみましょう!
ではテキストを開いてシミュレーションの旅に出発です🚀

はじめに
テキスト「数値シミュレーションで読み解く統計のしくみ」のご紹介
このシリーズは書籍「数値シミュレーションで読み解く統計のしくみ〜Rでためしてわかる心理統計」(技術評論社、「テキスト」と呼びます)の Python写経です。
テキストは、2023年9月に発売され、副題「Rでためしてわかる心理統計」のとおり、統計処理に定評のある R の具体的なコードを用いて、心理統計の理解に役立つ数値シミュレーションを実践する素晴らしい書籍です。
引用表記
この記事は、出典に記載の書籍に掲載された文章及びコードを引用し、適宜、掲載文章とコードを改変して書いています。
【出典】
「数値シミュレーションで読み解く統計のしくみ〜Rでためしてわかる心理統計」初版第1刷、著者 小杉考司・紀ノ定保礼・清水裕士、技術評論社
記事中のイラストは、「かわいいフリー素材集いらすとや」さんのイラストをお借りしています。
ありがとうございます!
3.4 任意の相関係数を持つ変数が従う確率分布
相関係数の値を指定して乱数生成するには・・・
この要件の答えが3.4節の実践で見つかるかもです。
この記事は Jupyter Notebook 形式(拡張子 .ipynb)でPythonコードを書きます。
概ね確率分布の特性値算出には scipy.stats を用い、乱数生成には numpy.random.generator を用いるようにしています。
主に利用するライブラリをインポートします。
### インポート
# 数値計算
import numpy as np
# データフレーム
import pandas as pd
# 確率・統計
import scipy.stats as stats
# 描画
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Meiryo'
3.4.1 相関係数と2変量正規分布
■ 2つの正規分布乱数とピアソンの積率相関係数
2つの正規分布乱数列を作成して、ピアソンの積率相関係数を算出します。
2つの変数は「数学テストの得点」と「身長」です。
### 106ページ 正規分布に従う2つの乱数の相関係数を算出
rng = np.random.default_rng(seed=123) # 乱数シードを指定
n = 100 # 標本サイズ
# 数学の点数が従う正規分布の平均
math_mu = 50
# 数学の点数が従う正規分布の標準偏差
math_sigma = 10
# 正規分布に従う、数学テストの得点の実現値
math = rng.normal(size=n, loc=math_mu, scale=math_sigma)
# 身長が従う正規分布の平均
height_mu = 160
# 身長が従う正規分布の標準偏差
height_sigma = 15
# 正規分布に従う、身長の実現値
height = rng.normal(size=n, loc=height_mu, scale=height_sigma)
# 相関係数の実現値
np.corrcoef(math, height)[0, 1]【実行結果】
相関係数はおよそ 0.06 。非常に小さな値です。
独立に生成した乱数なので相関係数が小さな値になることは当然のことなのかもです。

2つの乱数列の散布図を描画して相関関係を可視化しましょう。
### 106ページ 散布図の描画 107ページ図3.30
plt.figure(figsize=(6, 3))
plt.scatter(math, height, s=100, ec='royalblue', alpha=0.5)
plt.xlabel('math')
plt.ylabel('height');【実行結果】
相関関係が無さ気な散布図です。


■ 特定の相関係数の値の乱数を生成する
先の例では相関係数を定めず、ある意味乱数に任せて2変数の関係が生み出されました。
ここからは、特定の相関係数になるように乱数をコントロールします。
テキストの手順にしたがって、相関係数$${\rho=0.4}$$の乱数生成に取り組みます。
2変量正規分布を使用します。
2変量正規分布のパラメータは平均ベクトルと分散共分散行列です。
まず平均ベクトルを作成します。
### 108ページ 平均ベクトルの作成
# それぞれ、数学テストの得点と身長が従う正規分布の平均
mu_vec = np.array([math_mu, height_mu])【実行結果】なし
続いて分散共分散行列を作成します。
このコードにおいて、相関係数$${\rho=0.4}$$を織り込みます。
### 108ページ 分散共分散行列の作成
rho = 0.4 # 数学と身長が従う2変量正規分布の相関パラメータ
tau = rho * math_sigma * height_sigma # 数学得点と身長の共分散
# 分散共分散行列
cov_matrix = np.array([[math_sigma**2, tau],
[tau, height_sigma**2]])
cov_matrix【実行結果】

分散共分散行列から相関係数行列に変換します。
statsmodels の cov2corr 関数を利用します。
### 共分散行列を相関係数に変換するライブラリのインポート
from statsmodels.stats.moment_helpers import cov2corr### 109ページ 分散共分散行列から相関係数を復元
cov2corr(cov_matrix)【実行結果】
相関係数$${0.4}$$を導出できました。

乱数生成に進みます。
numpy random generator の multivariate_normal で多変量正規分布に従う乱数を2列、それぞれ2000個ずつ生成します。
引数は mean:平均ベクトル、cov:分散共分散行列です。
### 109ページ 平均ベクトルと分散共分散行列から任意の相関係数の実現値を持つ乱数を生成
rng = np.random.default_rng(seed=123)
dat_2norm = rng.multivariate_normal(mean=mu_vec, cov=cov_matrix, size=2000)
# 各変数に名前をつける。説明のために命名しているので、実用上は必須ではない
# pandasのデータフレーム化
colnames = ('math', 'height')
dat_2norm_df = pd.DataFrame(dat_2norm, columns=colnames)
dat_2norm_df.head()【実行結果】

生成した乱数の相関係数を算出します。
### 110ページ 相関係数の算出
dat_2norm_df.corr()【実行結果】
相関係数は$${0.40}$$です!ほぼ想定通りの値になりました!

生成した乱数の散布図を描画しましょう。
pandas の plot 機能を使ってみます。
### 110ページ 散布図の描画 図3.33
dat_2norm_df.plot.scatter(x='height', y='math', s=50, ec='white', alpha=0.5,
figsize=(6, 3));【実行結果】
ぼんやりと右肩上がりの傾向(弱い正の相関関係)が見られます。


3.4.2 3変量以上の多変量正規分布
3変量正規分布乱数を生成します。
3つの変数は「年齢」「数学テストの得点」「身長」です。
平均ベクトルと標準偏差ベクトルを作成します。
### 111ページ 3変量正規分布のパラメータの設定
age_mu = 15 # 年齢の平均
age_sigma = 2 # 年齢の標準偏差
# それぞれ、数学テストの得点、身長、年齢が従う正規分布の平均
mu_vec = np.array([math_mu, height_mu, age_mu])
# それぞれ、数学テストの得点、身長、年齢が従う正規分布の標準偏差
sigma_vec = np.array([math_sigma, height_sigma, age_sigma])【実行結果】なし
相関係数行列を作成します。
### 111ページ 相関係数マトリクスの作成
rho_matrix = np.array([[1, 0.4, 0.5],
[0.4, 1, 0.8],
[0.5, 0.8, 1]])
# 行名をつける。説明のために命名しているので、実用上は必須ではない
# pandasのデータフレーム化
names = ['math', 'height', 'age']
rho_matrix_df = pd.DataFrame(rho_matrix, index=names, columns=names)
rho_matrix_df【実行結果】
今回の乱数に織り込みたい相関係数です。

線形代数のテクを用いて、標準偏差ベクトルと相関係数行列から分散共分散行列を作成します。
@ は行列積(ドット積、内積)の演算子です。
### 112ページ 線形代数で分散共分散行列を作成
np.diag(sigma_vec) @ rho_matrix @ np.diag(sigma_vec)【実行結果】

平均ベクトルと分散共分散行列が揃いました。
3変量正規分布に従う乱数を2000個生成します。
### 112ページ 3変量正規分布に従う乱数の生成
rng = np.random.default_rng(seed=2)
dat_3norm = rng.multivariate_normal(
mean=mu_vec, cov=np.diag(sigma_vec) @ rho_matrix @ np.diag(sigma_vec),
size=2000)
colnames = ('math', 'height', 'age')
dat_3norm_df = pd.DataFrame(dat_3norm, columns=colnames)
dat_3norm_df.head()【実行結果】

3変数の相関係数を算出します。
### 113ページ 相関係数の算出
dat_3norm_df.corr()【実行結果】
相関係数の理論値とほぼ同じになりました!
相関係数を指定した乱数生成~シミュレーション~ができるようになりました!

(参考:相関係数の理論値)

3変数間の散布図を描画します。
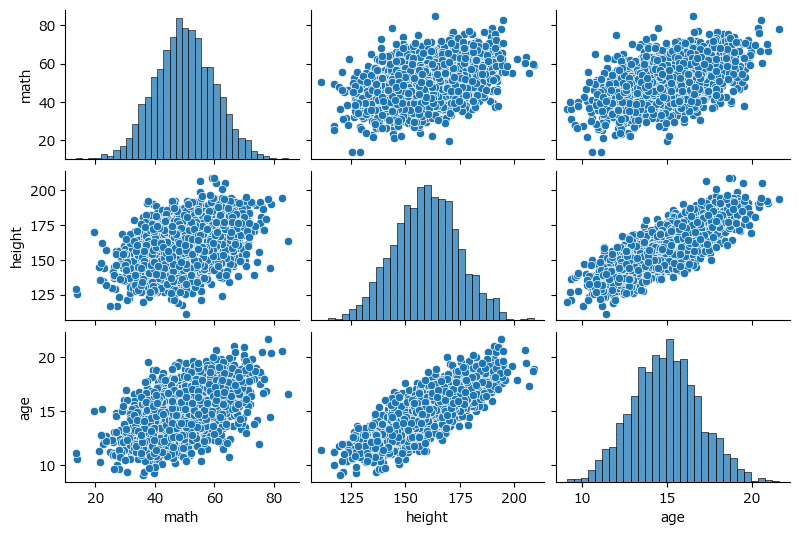
seaborn ライブラリの pairplot で散布図行列を描画します。
### 散布図行列を描画するライブラリのインポート
import seaborn as sns### 113ページ 散布図行列の描画
sns.pairplot(data=dat_3norm_df, height=1.8, aspect=1.5);【実行結果】
変数間の相関関係が一目瞭然ですね!

3.4.3 偏相関係数
■ 偏相関係数と共変数
「数学テストの得点」と「身長」の間の相関関係は、2つの変数の背後に「年齢」が影響しているかもしれません。
このような背後で影響する変数を「共変量」と呼ぶそうです。
そして共変量の影響を統制した(除いた)相関係数を「偏相関係数」と呼ぶそうです。
3つの変数の関係図を描画してみましょう。
テキストの図3.35に相当します。
グラフ描画に定評のある graphviz ライブラリを使用します。
### DAGを描画するライブラリのインポート
from graphviz import Digraph### 114ページ 共変量のイメージ 図3.35
## 設定
# 有向グラフオブジェクトの生成
g = Digraph()
# グラフのレイアウトの方向
g.graph_attr['rankdir'] ='UD'
# nodeの基本属性の設定
g.attr('node', shape='circle', fontname='Meiryo')
## node:頂点の作成、色面の塗り指定
g.node('年齢Z', fillcolor='moccasin', style='filled')
g.node('数学X', fillcolor='azure', style='filled')
g.node('身長Y', fillcolor='mistyrose', style='filled')
## edge:辺の作成
g.edge('年齢Z', '数学X')
g.edge('年齢Z', '身長Y')
## グラフの表示
g【実行結果】
年齢が共変量です。
数学と身長の間に矢印付きの関係性は無いのです。


■ 偏相関係数の計算例
年齢の影響を統制した数学テストの得点と身長の偏相関係数を算出します。
テキストにならって pcor3 関数を作成して、偏相関係数を求めます。
### 114ページ 共変量:年齢Zの影響を統制した数学Xと身長Yの偏相関係数の算出
# 3変数の偏相関係数を算出する関数
def pcor3(x, y, covariate):
# 偏相関係数の計算における分子
pcor_top = (
np.corrcoef(x, y)[0, 1]
- (np.corrcoef(x, covariate)[0, 1] * np.corrcoef(y, covariate)[0, 1]))
# 偏相関係数の計算における分母
pcor_bottom = (np.sqrt(1 - np.corrcoef(x, covariate)[0, 1]**2)
* np.sqrt(1 - np.corrcoef(y, covariate)[0, 1]**2))
return pcor_top / pcor_bottom
# 数学テスト得点と身長の偏相関係数の算出
pcor3(x=dat_3norm_df.math, y=dat_3norm_df.height, covariate=dat_3norm_df.age)【実行結果】
偏相関係数の実現値はほぼ0です。
年齢の影響を統制すると数学力と身長の間には直線的な関係がほとんど無い、と考えられます。

回帰分析を用いて偏相関係数を算出できるそうです。
テキストにならってトライしてみます!
statsmodels の ols で回帰分析を実行します。
残差の相関を見ます。
### 回帰分析をformula構文で実行するライブラリのインポート
import statsmodels.formula.api as smf### 115ページ 回帰分析を用いて偏相関係数を計算する方法
# 数学が目的変数、年齢が説明変数の回帰分析。残差を取得
residual_math = smf.ols('math ~ age', data=dat_3norm_df).fit().resid
# 身長が目的変数、年齢が説明変数の回帰分析。残差を取得
residual_height = smf.ols('height ~ age', data=dat_3norm_df).fit().resid
# 偏相関係数の算出 残差同士の相関係数
np.corrcoef(residual_math, residual_height)[0, 1]【実行結果】
pcor3 関数の計算結果とほぼ同じになりました!

pingouin ライブラリに偏相関係数を算出する関数があります。
試してみましょう。
### 偏相関係数を算出するライブラリのインポート
import pingouin as pg### 偏相関係数の算出
dat_3norm_df.pcorr()【実行結果】
1行目・2列目に数学の得点と身長の偏相関係数$${0.022068}$$が表示されました!
Pythonで偏相関係数を求める際は pingouin を活用しましょう。


■ 偏相関係数のシミュレーション
共変量「年齢」と「身長」の相関係数の変化によって、「数学テストの得点」と「身長」の偏相関係数がどのように変化するかをシミュレーションします。
### 116ページ 共変量とYの相関係数を変化させてXとYの偏相関係数の変化を確認
# 年齢と身長の相関係数(0~0.9)
rho_age_height = np.round(np.arange(0, 0.91, 0.3), 1)
rng = np.random.default_rng(seed=123)
for i in range(len(rho_age_height)):
rho_matrix = np.array([[1, 0.4, 0.5],
[0.4, 1, rho_age_height[i]],
[0.5, rho_age_height[i], 1]])
dat_3norm = rng.multivariate_normal(size=2000,
mean=mu_vec, cov=np.diag(sigma_vec) @ rho_matrix @ np.diag(sigma_vec))
pcorr = pcor3(dat_3norm[:, 0], dat_3norm[:, 1], dat_3norm[:, 2])
print(f'年齢(共変量)と身長のρ = {rho_age_height[i]}, ',
f'数学と身長の偏相関係数 = {pcorr:.4f}')【実行結果】
共変量・年齢と身長の相関係数 ρ が大きくなるにつれて、数学と身長の偏相関係数が小さくなることが分かります。
共変量の存在によって、本来弱い相関関係のはずの変数間の相関係数が強く見えることがあるそうです。


3.5 演習問題
3.5.1 演習問題1
自由度5のt分布に従う確率変数が2以上の値を取る確率です。
### 117ページ 3.5.1 演習問題 自由度5のt分布に従う確率変数Tが2≦T<∞の値をとる確率
1 - stats.t.cdf(x=2, df=5)【実行結果】

別解です。
### 117ページ 3.5.1 演習問題 別解
stats.t.sf(x=2, df=5)【実行結果】

3.5.2 演習問題2
自由度(10,30)のF分布乱数を2000個生成してヒストグラムを描画します。
### 117ページ 3.5.2 演習問題2
# 自由度(10,30)のF分布に従う乱数を2000個生成してヒストグラムを描画
## 乱数の生成
rnf = np.random.default_rng(seed=123)
f_rand = rng.f(dfnum=10, dfden=30, size=2000)
## ヒストグラムの描画
# 描画領域の設定
fig, ax = plt.subplots(figsize=(6, 3))
# f分布乱数のヒストグラムの描画
ax.hist(f_rand, bins=35, density=True, ec='white', alpha=0.7)
# 修飾
ax.set(xlabel='f', ylabel='Density', title='Histogram of f')
plt.tight_layout();【実行結果】

3.5.3 演習問題3
共変量ZとXの相関係数を変化させてXとYの偏相関係数の変化を確認します。
### 117ページ 3.5.3 演習問題
# 共変量ZとXの相関係数を変化させてXとYの偏相関係数の変化を確認
# rho=0.9のときmultivariate_normalの処理でワーニングが発生する
# 年齢と身長の相関係数(0~0.9)
rho_age_math = np.round(np.arange(0, 0.91, 0.3), 1)
rng = np.random.default_rng(seed=123)
for i in range(len(rho_age_math)):
rho_matrix = np.array([[1, 0.4, rho_age_math[i]],
[0.4, 1, 0.8],
[rho_age_math[i], 0.8, 1]])
dat_3norm = rng.multivariate_normal(size=2000,
mean=mu_vec, cov=np.diag(sigma_vec) @ rho_matrix @ np.diag(sigma_vec))
pcorr = pcor3(dat_3norm[:, 0], dat_3norm[:, 1], dat_3norm[:, 2])
print(f'年齢(共変量)と数学の得点のρ = {rho_age_height[i]}, ',
f'数学と身長の偏相関係数 = {pcorr:.4f}')【実行結果】

今回の写経は以上です。
シリーズの記事
次の記事
前の記事
目次
ブログの紹介
note で7つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。
2.実験!たのしいベイズモデリング1&2をPyMC Ver.5で
書籍「たのしいベイズモデリング」・「たのしいベイズモデリング2」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.実験!岩波データサイエンス1のベイズモデリングをPyMC Ver.5で
書籍「実験!岩波データサイエンスvol.1」の4人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう!
4.楽しい写経 ベイズ・Python等
ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀
5.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん!
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。
6.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
7.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
最後までお読みいただきまして、ありがとうございました。
