12章 Irisデータセットの訓練でエラー発生！！

はじめに

シリーズ「Python機械学習プログラミング」の紹介

本シリーズは書籍「Python機械学習プログラミング PyTorch & scikit-learn編」（初版第1刷）に関する記事を取り扱います。
この書籍のよいところは、Pythonのコードを動かしたり、アルゴリズムの説明を読み、ときに数式を確認して、包括的に機械学習を学ぶことができることです。
Pythonで機械学習を学びたい方におすすめです！
この記事では、この書籍のことを「テキスト」と呼びます。

Python機械学習プログラミング［PyTorch＆scikit-learn編］ (impress top gear)

記事の内容

この記事は「第12章 ニューラルネットワークの訓練をPyTorchで並列化する」の「12.4.4 Irisデータセットの花の品種を分類する多層パーセプトロンを構築する」の中程で、エポック数を100に指定して分類モデルを構築するコードを実行する際に発生するエラー対処方法を取り上げています。

12章のダイジェスト

12章からPyTorchにチャレンジします。
PyTorchはディープラーニングツールです。いよいよ機械学習の核心に近づいてまいりました！
まずはPyTorchをインストールして、PyTorch特有のデータ型であるテンソル（torch.Tensor）の簡単な操作を行います。
次に、torchvision.datasetsライブラリの画像データセットを操作する練習を行います。
さらには、PyTochの「torch.nn」と「torch.optim」を用いてディープラーニングアーキテクチャに触れたり、活性化関数の選択に関する話題を検討します。
Pytorchによる多クラス分類タスクの構築で使用するのが、MNISTのIrisデータセットです。機械学習のさまざまなテキストで用いられている、あのアヤメが3種類に分類されたデータセットです。

---

PyTorchでアヤメ分類の訓練を実行できるようにする

エラー発生の原因の特定

Irisデータセットの分類タスクにおいて、テキストに記載された訓練コードの実行時にエラーが発生しました。エラー 発生箇所は、loss_fn です。

# エラー発生箇所
loss = loss_fn(pred, y_batch)

loss_fn は torch.nn の交差エントロピー損失関数  nn.CrossEntropyLoss() のインスタンスです。
つまり、loss_fn は損失関数です。

# loss_fnは交差エントロピー損失関数
loss_fn = nn.CrossEntropyLoss() 

次のエラーメッセージが表示されました。

損失関数の実行エラー

RuntimeError: expected scalar type Long but found Int
スカラーのlong型を期待しましたが、int型が見つかりました。

エラーの原因は、どうやら型が合わないことのようです。
torch.Tensor のデータ型dtypeでは、long 型とinit 型は次のように異なるようです。
- torch.long 型 : 64ビット符号あり整数
- torch.int 型 : 32ビット符号あり整数

エラーが生じた loss_fn 損失関数の引数 pred と y_batch のどちらのデータ型に問題があるか、よくわからなかったので、ここでは奥の手の・・・
「GitHubからダウンロードしたサンプルコードを確かめる」
を実施します。
ひとまず、GitHubのサンプルコードを実行すると、なんと正常終了するのです。
そこで、ソースコードを確認しました。
驚愕の事実の発覚です！！！

驚愕の事実の発覚

GitHubのサンプルコードでは y_batch 引数を long 型に変換 していたのです。
問題はあっさり解決です。
ただ・・・
テキストとGitHubのサンプルコードが違っているのって、もやもやします。
最後に、正常に動いたサンプルコードを添えておきます。

# Irisデータセットの分類モデルを訓練するコード
num_epochs = 100
loss_hist = [0] * num_epochs
accuracy_hist = [0] * num_epochs

for epoch in range(num_epochs):

    for x_batch, y_batch in train_dl:        # モデルの訓練
        pred = model(x_batch)                # 1.予測値を生成
        loss = loss_fn(pred, y_batch.long()) # 2.損失値を計算
        loss.backward()                      # 3.勾配を計算
        optimizer.step()                     # 4.勾配を使ってパラメータを更新
        optimizer.zero_grad()                # 5.勾配を0にリセット

        loss_hist[epoch] += loss.item()*y_batch.size(0)
        is_correct = (torch.argmax(pred, dim=1) == y_batch).float()
        accuracy_hist[epoch] += is_correct.sum()

    loss_hist[epoch] /= len(train_dl.dataset)
    accuracy_hist[epoch] /= len(train_dl.dataset)

無事に次の作業に進むことができました。
この 12.4.5 節の最後に作成した訓練モデルの学習曲線（損失率、正解率）のグラフを若干アレンジしたものは次のようになりました。

各エポックの損失値と正解率

---

まとめ

今回は、PyTorchのデータ型に関するエラーの解消に取り組みました。
PyTorchのテンソルに慣れるにはまだまだ時間がかかりそうです。

追伸：　テキストの正誤
12章最後に記載の「表 12-2: 本書で取り上げる活性化関数」の計算式に誤りがある感じなので、その部分の正誤（案）を記載して締めようと思います。

活性化関数：区分線形の方程式

【誤りと思われる式】

$$
\sigma(z)=
\begin{cases}
0, &z\leq \mathbf{\frac{1}{2}} \\
z+\frac{1}{2}, & -\frac{1}{2} \leq z \leq \frac{1}{2} \\
1, & z\geq \mathbf{-\frac{1}{2}} \\
\end{cases}
$$

【おそらく正しい式】

$$
\sigma(z)=
\begin{cases}
0, &z\leq \mathbf{-\frac{1}{2}} \\
z+\frac{1}{2}, & -\frac{1}{2} \leq z \leq \frac{1}{2} \\
1, & z\geq \mathbf{\frac{1}{2}} \\
\end{cases}
$$

GitHubからダウンロードしたサンプルコードに添付の表が正しいと思われます。

活性化関数：区分線形の場合
（サンプルコードより転載）

書籍の編集作業の大変さを噛み締めました。

# 今日の一句
print('原書のサンプルコードの正解率は高そうである')

楽しくPython機械学習プログラミングを学びましょう！

おまけ数式

noteでは数式記法を利用できます。
今回はニューラルネットワークの活性化関数として用いられるReLU関数の式を紹介します。

$$
\sigma (z) = \mathrm{max(0, z)}
$$

シンプルですが、勾配消失問題に対して強みのある活性化関数だそうです。
グラフはこんな感じになります。はみ出しました。

活性化関数のプロット：tanh, logistic, ReLU

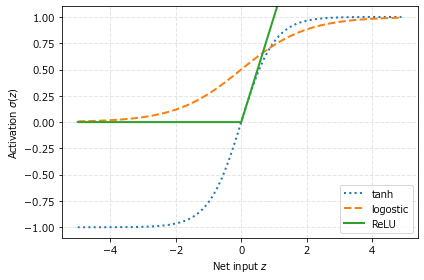
グラフ作成のサンプルコードを添えておきます。
「図12-9 : tanh関数とlogistic関数の比較」のコードを改造しました。

# 3種類の活性化関数プロット　logistic、tanh、ReLU
import numpy as np
import matplotlib.pyplot as plt

def logistic(z):
    return 1.0 / (1.0 + np.exp(-z))
def tanh(z):
    e_p = np.exp(z)
    e_m = np.exp(-z)
    return (e_p - e_m) / (e_p + e_m)
def relu(z):
    return z * (z > 0.0)

z = np.arange(-5, 5, 0.1)
log_act = logistic(z)
tanh_act = tanh(z)
relu_act = relu(z)

plt.ylim([-1.1, 1.1])
plt.xlabel('Net input $z$')
plt.ylabel('Activation $\sigma(z)$')  # sigmaの前に\を付ける
plt.grid(linestyle='--', lw=1, alpha=0.6, color='lightgray')
plt.plot(z, tanh_act, linewidth=2, linestyle=':', label='tanh')
plt.plot(z, log_act, linewidth=2, linestyle='--', label='logostic')
plt.plot(z, relu_act, linewidth=2, linestyle='-',label='ReLU')
plt.legend(loc='lower right')
plt.tight_layout()
plt.show()

---

おわりに

AI・機械学習の学習でおすすめの書籍を紹介いたします。
「日本統計学会公式認定　統計検定２級　公式問題集［CBT対応版］」

日本統計学会公式認定　統計検定　2級　公式問題集［CBT対応版］

データサイエンスの基礎を補強する上で、確率・統計の知識は欠かせないものになっています。
統計分野の資格の代表格が「統計検定」。
そして、統計検定２級の公式問題集がCBT対応になって新発売です！
CBT方式とは、コンピュータを利用して実施する試験方式です。
これまでの公式問題集は紙ベースのPBT方式試験時代の問題を掲載していました。紙の時代の問題はとても味わい深いのですが、CBT方式の問題と整合していないこともあり、CBT試験の訓練としてはいまひとつ、手応えを感じにくい面がありました。
試験対策がしやすくなった今が、統計検定２級にチャレンジするいいタイミングではないでしょうか。
いずれは、このnoteで統計検定２級のCBT試験解読の記事を書いてみたいです（時間がほしいです）。

最後まで読んでくださり、ありがとうございました。