1-1 相対度数の計算〜都道府県別大学・大学院数の可視化

ネイピア DS

2023年2月25日 21:01

今回の統計トピック

度数分布表、ヒストグラム、箱ひげ図を作成します！

公式問題集の準備

「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください！
「知る」「実践する」の章で、のんびり統計をお楽しみください！

問題を解く

📘公式問題集のカテゴリ

1変数記述統計の分野
問1 相対度数の計算（都道府県別の大学数）

試験実施年月
統計検定2級 2018年11月問1（回答番号1）

問題

公式問題集をご参照ください。

解き方

相対度数分布表は、度数分布表の各階級の度数を全度数の合計で割った割合を記載します。
したがって、相対度数分布表の縦合計は1.0または100%になります。
この問題は単位が%であり、縦合計は100%です。

1985年では、明かされている相対度数が85.1と2.1で合計は87.2です。
（ア）を埋めて縦合計が100%になるように、「100－87.2＝12.8」を計算します。
（ア）は12.8です。
2017年では、明かされている相対度数が76.6、17.0、2.1で合計は95.7です。
（イ）を埋めて縦合計が100%になるように、「100－95.7＝4.3」を計算します。
（イ）は4.3です。

解答

⑤（ア）12.8、（イ）4.3です。

難易度　やさしい

・知識：度数分布表
・計算力：電卓（低）
・時間目安：1分

知る

おしながき

公式問題集の問題に接近してみましょう！
ここでは「2022年の都道府県別大学・大学院数データ」を利用します。
大学本部所在地の都道府県にカウントされています。
記事では大学・大学院をまとめて「学校」と呼びます。

【出典記載】
出典：「学校基本調査」（文部科学省）
【コンテンツ編集・加工の記載】
記事の記載にあたっては、「学校基本調査」（文部科学省）を加工して作成しています。

度数分布表

📕公式テキスト：1.2.1 ヒストグラムの作成（6ページ）、1.2.2 その他の図表の作成（10ページ～）

度数分布表は「1変数」を要約記述する表です。
次の図は度数分布表のサンプルです。
各項目の内容は脚注をご覧ください。

この度数分布表は、各都道府県別学校数データに基づいて、０～19校設置する都道府県、20～39校設置する都道府県といった一定の範囲（階級）に層別して、都道府県数をカウントしたものです。
学校を0～19校を設置するのは35都道府県、20～39校設置は9都道府県、というように読みます。
値の低い階級に偏っているように見えます。
相対度数を見ると、75%の都道府県は19校以下、93%の都道府県は39校以下、ということを読み取れます。

元データ（1変数の真意）
次の表は度数分布表の元になる「2022年の都道府県別大学・大学院数データ」です。

度数分布表のカウント対象のデータ項目は「学校数」です。
カウント対象のデータが1項目「学校数」だけなので、「1変数」の記述ということになります。
つまり、このデータから都道府県を取り除き、学校数の１項目だけのデータにしても、度数分布表を作成することができます。
たとえば、学校数が40～59のデータ数は2個、というように階級ごとに学校数項目を数え上げればいいのです。

ヒストグラム

📕公式テキスト：1.2.1 ヒストグラムの作成（6ページ～）

「ヒストグラム」は度数分布表と表裏一体のグラフです。
次の図はヒストグラムのサンプルです。

度数分布表を基にしてヒストグラムを作成します。
x軸（横軸）に階級（学校数）、y軸（縦軸）に度数（都道府県数）をプロットします。
全体的に左側に偏っていること、1都道府県（東京都）だけ140～160校の階級にポツリと存在することが分かります。
なお、階級の幅を広くしたり、狭くしたりすることで、グラフ表現が変わります。
都道府県の設置状況・傾向がもっと違って見えてくるかもしれません。
度数分布表のような数字表現は具体的な値を知るのに役立ち、ヒストグラムのような図による表現は概観を直感的に把握するのに役立ちます。

箱ひげ図

📕公式テキスト：1.4.2 箱ひげ図（22ページ～）
箱ひげ図も1変数データの表現の仲間です。
次の図は箱ひげ図のサンプルです。
各項目の内容は図中の説明をご覧ください。

箱ひげ図は都道府県別大学・大学院数データを要約しています。
特徴的なのは四分位関連の数値をグラフ表現して、データ分布の特徴を大まかに把握できることです。
第1四分位数、第2四分位数（中央値）、第3四分位数を求めて青色部分の「箱」を表現します。
また、データの最小値・最大値を求めて縦棒の「ひげ」を表現します。
ひげの下辺・上辺に対して下限値、上限値を定めることもあります。
上の図では、最大値が上限値を超えるため、ひげの上辺を上限値にしています。
下限値・上限値の範囲外のデータ点は「外れ値」と呼ばれます。
箱の大きさ、ひげの長さ、外れ値の点在を把握して、データの傾向を読み取ります。
箱ひげ図では、データの下方の偏りと飛び抜けて学校が多い都道府県があることが一目瞭然です。

実践する

度数分布表、ヒストグラム、箱ひげ図を作成してみよう

2022年度の都道府県別大学・大学院数は、政府統計の総合窓口「e-Stat」で公開されています。

次のリンクで2022年度の都道府県別大学・大学院数のダウンロードサイトを開くことができます。

学校基本調査－令和４年度高等教育機関《報告書掲載集計》学校調査大学・大学院

2022年都道府県別大学・大学院数CSVファイルのダウンロード
こちらのリンクから整形後のCSVファイルをダウンロードできます。
Pythonサンプルファイルを利用する方は、このCSVファイルをダウンロードしてください。

電卓・手作業で作成してみよう！

上述の方法でデータを取得して、電卓やそろばんをはじいて、手作業で度数集計表、ヒストグラム、箱ひげ図を書いてみましょう！
一番記憶に残る方法ですし、試験本番の電卓作業のトレーニングにもなります。

EXCELで作成してみよう！

データ数が多い場合、やはり手作業では非効率になります。
パソコンを利用して、手早く作表できるようになれば、実務活用がしやすくなるでしょう。

度数分布表

度数を計算する「FREQUENCY」関数を使います。

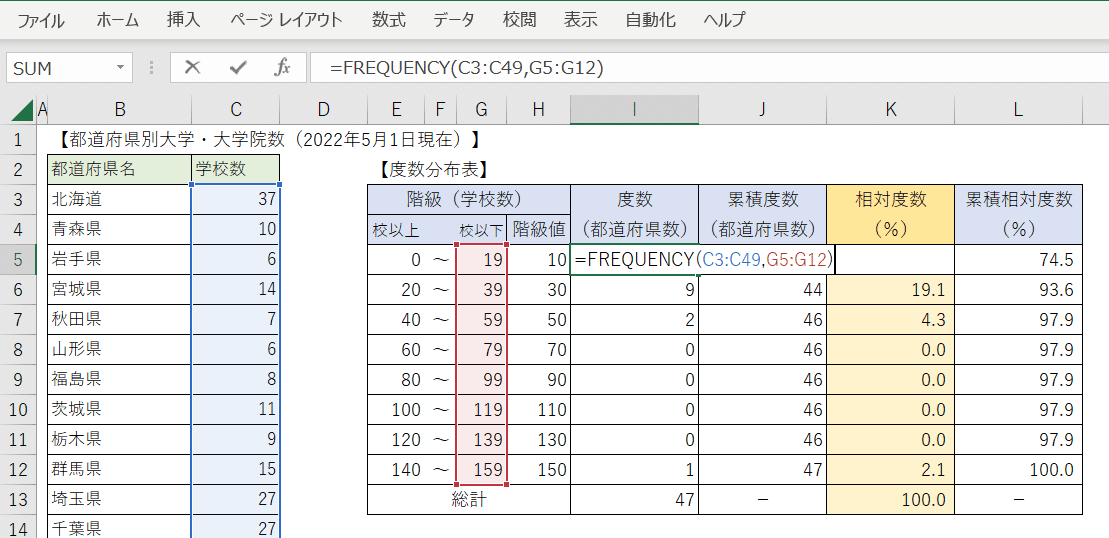
=FREQUENCY( 「カウントするデータの範囲＝都道府県別学校数, 「階級の上限値＝階級の校以下」 )を引数指定します。

累積度数、相対度数、累積相対度数は、EXCELの足し算、割り算で計算できます。

ヒストグラム

①メニュー選択
度数分布表の階級の上限値（校以下）と度数を範囲指定してから、「メニュー」→「挿入」→「グラフ」の右下の矢印をクリックします。

②グラフの作成
縦棒グラフを選びます。
画面に現れたグラフ（案）に対して、タイトルなどの変更をします。

箱ひげ図

都道府県別学校数の表の「学校数」を範囲指定してから、「メニュー」→「挿入」→「グラフ」→右下の矢印をクリックします。
グラフの挿入画面で箱ひげ図を選んで「OK」をクリックします。
画面に現れた箱ひげ図（案）に対して、タイトルや大きさなどの変更を行います。

EXCELサンプルファイルのダウンロード
こちらのリンクからEXCELサンプルファイルをダウンロードできます。

Pythonで作成してみよう！

プログラムコードを読んで、データを流したりデータを変えてみたりして、データを追いかけることで、作表ロジックを把握する方法も効果的でしょう。
サンプルコードを揃えておけば、類似する作表作業を自動化して素早く結果を得ることができます。

【謝辞】
度数分布表のコードについては、次のサイトを参考にしました。
ありがとうございました！

①ライブラリのインポート
主にpandasを使用します。

import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
%matplotlib inline
plt.rcParams['font.family'] = 'MS Gothic'

②CSVファイルの読み込み
まず、上述のダウンロードリンクより、CSVファイルをダウンロードします。
その後、次のコードを実行して、CSVファイルをpandasのデータフレームに読み込みます。

datafile = './sample_data.csv'  # 格納フォルダとCSVファイル名を設定してください。
df = pd.read_csv(datafile)
df.head()

③要約統計量の表示
pandasのdescribeで平均、標準偏差、四分位関連数値を表示します。

df.describe()

次のような要約統計量が表示されます。

④度数分布表の作成
階級、度数、階級値、相対度数、累積度数、累積相対度数をそれぞれ計算してから、pandasのデータフレームで度数分布表データを作成します。

bins = np.linspace(0, 160, 9)                        # 階級
freq = df['num'].value_counts(bins=bins, sort=False) # 度数
class_value = (bins[:-1] + bins[1:]) / 2             # 階級値
rel_freq = round(freq / df['num'].count() * 100, 1)  # 相対度数
cum_freq = freq.cumsum()                             # 累積度数
cum_rel_freq = rel_freq.cumsum()                     # 累積相対度数
df_freq = pd.DataFrame({'階級超': bins[:-1], '階級以下': bins[1:],
                        '階級値': class_value,
                        '度数': freq, '累積度数': cum_freq,
                        '相対度数': rel_freq, '累積相対度数': cum_rel_freq},
                       index=freq.index)
df_freq

補足：かっこによる範囲表記
( 20.0, 40.0 ] のかっこの表記は、20超40以下を示しています。
( ) 丸かっこは範囲の端を含まず、[ ] 角かっこは範囲の端を含みます。
( 0, 10 ) は 0 超 10 未満、[ 0, 10 ]は 0 以上 10 以下、[ 0, 10 ) は 0 以上 10 未満をそれぞれ表します。

⑤ヒストグラムの作成
度数分布表データフレームからpandasのplotを利用してヒストグラムを作成します。
下から2行目のコメントを外すと、ヒストグラムの画像ファイルを指定したフォルダに保存できます。

df_freq.plot.bar(
    figsize=(4, 4), fontsize=8, width=1,
    color='royalblue', edgecolor='lightgray', linewidth=0.8,
    x='階級値', y='度数', title='ヒストグラム',
    label='都道府県数',
    xlabel='大学・大学院数 （階級値）',
    ylabel='都道府県数（度数）')
    plt.xticks(rotation=30)     # x軸目盛り：階級値を回転
plt.tight_layout()
# plt.savefig('./hist.png') # ヒストグラム画像ファイルの保存
plt.show()                  # ヒストグラムの表示

⑥箱ひげ図の作成
CSVファイルを読み込んだデータフレームを基にして、pandasで箱ひげ図を作成します。シンプルなコードで作成できます。

df['num'].plot.box(figsize=(1, 4), showmeans=True)
plt.show()

⑦（参考）度数分布表データフレームをCSVファイルに保存
次のコードで度数分布表データフレームをCSVファイルにして保存できます。
保存フォルダとファイル名を適宜変更してください。

df_freq.to_csv('./df_freq.csv', encoding='utf_8_sig') # 保存フォルダ・ファイル名を設定

Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。

おわりに

最初の投稿ということで、気合を入れてさまざまな情報発信に取り組みました。
情報過多な面もありそうですし、主要論点の抜け漏れがあるかもしれません。
また、表現のよしあしもありそうです。
逐次的に改善を重ねてよりより情報発信を目指していきます！
ご要望やご感想がありましたら、コメントをしていただけると嬉しいです。
今後もよろしくお願いいたします。

最後までお読みいただきまして、ありがとうございました。

のんびり統計シリーズの記事

次の記事

いいなと思ったら応援しよう！

この記事が参加している募集

#新生活をたのしく

47,053件

1-1 相対度数の計算 〜 都道府県別大学・大学院数の可視化

今回の統計トピック

問題を解く

知る

おしながき

度数分布表

ヒストグラム

箱ひげ図

実践する

度数分布表、ヒストグラム、箱ひげ図を作成してみよう

電卓・手作業で作成してみよう！

EXCELで作成してみよう！

Pythonで作成してみよう！

おわりに

のんびり統計シリーズの記事

いいなと思ったら応援しよう！

この記事が参加している募集

1-1 相対度数の計算〜都道府県別大学・大学院数の可視化