
時系列分析入門【第4章 その6】WAIC算出・交差検証のための時系列分割をPythonとPyMC Ver.5 で実践する
この記事は、テキスト「RとStanではじめる 心理学のための時系列分析入門」の第4章「RStanによる状態空間モデル」のRスクリプト・Stanコードをお借りして、PythonとPyMC Ver.5 で「実験的」に実装する様子を描いた統計ドキュメンタリーです。
取り扱いテーマは時系列データのベイズモデル選択で利用する「WAIC」「時系列データの交差検証」を実践します。
今回はPyMCでモデリングします。
まぁまぁ、諸々はさておいて、時系列分析とベイズモデリングを楽しんでいきましょう!
テキストの紹介、引用表記、シリーズまえがきは、このリンクの記事をご参照ください。
テキストで使用するデータは、R・Stan等のサンプルスクリプトで指定されています。
サンプルスクリプトは著者GitHubサイトからダウンロードして取得できます。
第4章 RStanによる状態空間モデル
この記事は「4.5 モデル選択」を実践いたします。
インポート(+環境準備)
この記事で用いるライブラリをインポートします。
### インポート
# 基本
import numpy as np
import pandas as pd
# Rデータセット・一般化線形モデル・時系列分析
import statsmodels.api as sm
# PyMC
import pymc as pm
import arviz as az
# 時系列CV
from sklearn.model_selection import TimeSeriesSplit
# グラフ描画
import matplotlib.pyplot as plt
# import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'
# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')【補足】PyMC環境の構築
AnacondaでPyMC環境を構築する方法を次のリンクの「pymc環境の構築」の箇所に記載しています。
ご参考まで。

WAIC
ベイズモデルのモデル選択の際に利用される指標「WAIC」を算出します。
テキストは「時系列データはデータの独立性がないためWAICなどの情報量規準を適用できないという指摘があります」との注釈を掲載しています。
① データの作成・前処理
ランダムウォークの時系列データを作成します。
なお、生成する乱数がテキストと異なるため、出来上がったデータ&WAICの値もテキストと異なる結果になることを予めご了承くださいませ。
### データの作成
# 初期値設定
N = 100 # 期間
np.random.seed(123)
# ランダムウォークの時系列を作成
Y = np.cumsum(np.random.randn(N))
# データフレーム化
df_waic = pd.DataFrame({'Time': range(1, N+1), 'Y': Y})
# 描画
df_waic['Y'].plot(figsize=(10, 3), xlabel='Time', ylabel='Y');【実行結果】
期間100のランダムウォークデータです。

② モデルの定義
システムモデル(レベル成分)の記述には「pm.GaussianRandomWalk()」を利用しました。
### モデルの定義
# モデルの定義
with pm.Model() as model_rw:
### データ関連定義
# coordの定義
model_rw.add_coord('data', values=df_waic.index, mutable=True)
model_rw.add_coord('time', values=df_waic['Time'].values, mutable=True)
# dataの定義
y = pm.ConstantData('y', value=df_waic['Y'].values, dims='time')
### 事前分布
# muのシステムノイズ
sigmaS = pm.Uniform('sigmaS', lower=0, upper=100)
# 観測ノイズ
sigmaO = pm.Uniform('sigmaO', lower=0, upper=100)
### mu:システムモデル
init_dist = pm.Normal.dist(mu=0, sigma=sigmaS)
mu = pm.GaussianRandomWalk('mu', sigma=sigmaS, # init_dist=init_dist,
dims='time')
### 尤度:観測モデル
likelihood = pm.Normal('likelihood', mu=mu, sigma=sigmaO, observed=y,
dims='time')【実行結果】出力なし
③ モデルの表示・可視化
モデルの数式を表示します。
### モデルの表示
model_rw【実行結果】

モデルを図にして可視化しましょう。
# モデルの可視化
pm.model_to_graphviz(model_rw)【実行結果】

④ 事後分布からのサンプリング
MCMCを実行します。
WAICの計算に使用する対数尤度データをサンプリング実行時に同時生成します。
pm.sample()の引数で次をコードを指定します。
idata_kwargs={'log_likelihood': True}
NUTSサンプラーにnumpyroを利用します。
実行時間はおよそ20秒でした。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 20秒
with model_rw:
idata_rw = pm.sample(draws=2000, tune=10000, chains=4, target_accept=0.95,
idata_kwargs={'log_likelihood': True},
nuts_sampler='numpyro', random_seed=1234)【実行結果(一部)】

⑤ サンプリングデータの確認
$${\hat{R}}$$、事後分布の要約統計量、トレースプロットを確認します。
事後分布の収束確認は$${\hat{R} \leq 1.1}$$としています。
### r_hat>1.1の確認
# 設定
idata_in = idata_rw # idata名
threshold = 1.1 # しきい値
# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in) > threshold).sum().data_vars)【実行結果】
$${\hat{R}>1.1}$$のパラメータは「0」件です。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

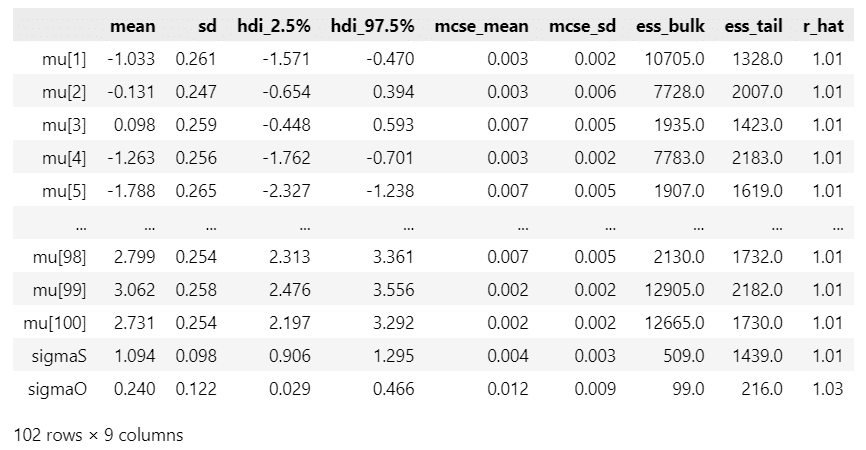
パラメータ等の事後分布の要約統計量です。
### 推論データの要約統計情報の表示
pm.summary(idata_rw, hdi_prob=0.95)【実行結果】
トレースプロットを確認しましょう。
### トレースプロットの表示
pm.plot_trace(idata_rw, combined=True, figsize=(10, 5))
plt.tight_layout();【実行結果】
収束している感じがします。

⑥ WAICの算出
arvizのwaic()を利用します。
構文はシンプルです。
az.waic( idata )
テキストに付属のRコードの出力結果の形式に真似て作ってみました。
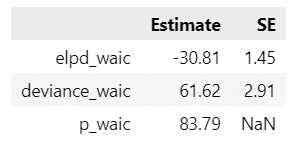
### WAICの算出
# log-score
waic_rw_log = az.waic(idata_rw, scale='log')
# -2*log-score
waic_rw_dev = az.waic(idata_rw, scale='deviance')
# データフレーム化
waic_df = pd.DataFrame({'Estimate': [waic_rw_log.elpd_waic,
waic_rw_dev.elpd_waic, waic_rw_log.p_waic],
'SE': [waic_rw_log.se, waic_rw_dev.se, np.nan]},
index=['elpd_waic', 'deviance_waic', 'p_waic'])
display(waic_df.round(2))【実行結果】
az.waic()のscale引数で「log」(elpd表示)と「deviance」を指定しました。
waicの詳細はarviz公式サイトで確認しましょう。
WAICとともによく用いられる指標「LOO」の計算を行ってみましょう。
### LOOの計算
az.loo(idata_rw)【実行結果】
パレートk診断の結果は良くないようです(0.7を超えるとモデルの指定が不十分とのこと)。

LOOに関する詳細もarviz公式サイトで確認しましょう。
なんとなく後味が悪いので、ここはひとつ、事後予測を楽しみましょう。
目的変数の事後予測サンプリングを行います。
### 事後予測のサンプリングの実施
with model_rw:
idata_rw.extend(pm.sample_posterior_predictive(idata_rw))【実行結果】省略
続いて事後予測をプロットします。
plot_ppc()を利用します。
### 事後予測プロット
fig, ax = plt.subplots(figsize=(10, 4))
pm.plot_ppc(idata_rw, num_pp_samples=100, random_seed=1234, ax=ax)
ax.set(title='事後予測プロット', xlabel='Y', ylabel='density');【実行結果】
黒線の観測データとオレンジ点線の事後予測平均データは重なって見えます。
目的変数の予測値はいい感じですね。


時系列データの交差検証
モデルの予測性能を高めたり、予測性能の高いモデルを選択するために交差検証を行うことがあります。
詳しい内容はテキストをご覧ください。
ポイントは、時系列データの場合、未知である未来データで学習して過去データで検証するのはよくないので、時系列の順序に沿って学習データと検証データを分割しよう、ということです。
① データの読み込み
Rの標準データセット「AirPassengers」を statsmodels(sm)を利用して pandas のデータフレイムに読み込みます。
### データセットの読み込み
# Rデータセットの読み込み:第1引数:Item, 第2引数:Package
df_air = sm.datasets.get_rdataset('AirPassengers', 'datasets').data
# 月インデックスの設定, time列の削除
df_air.index = pd.period_range(f'{int(df_air.iloc[0, 0])}-01-01',
periods=len(df_air), freq='m')
df_air = df_air.drop(columns='time')
# データフレームの表示
display(df_air)【実行結果】
12年間の月別飛行機乗客数データです。

グラフにしてみましょう。
### 描画
df_air.plot(figsize=(10, 3), xlabel='Time', ylabel='乗客数', legend=False);【実行結果】
右肩上がりのトレンドとおそらく12か月の周期性が見られます。

② 時系列を考慮した交差検証のデータ分割:学習データを徐々に追加
scikit-learnのTimeSeriesSplit()を利用して分割します。
この関数は学習データと検証データの「インデックス」を取得するまでを行うので、別途、データそのものを取得する処理を行う必要があります。
また、データセットが時系列順に並んでいる必要があります。
### 時系列を考慮した交差検証のデータ分割 (1)学習データを徐々に追加する方法
# 時系列CVのインスタンス生成 10分割、検証データ12か月、学習データを徐々に追加
tscv = TimeSeriesSplit(n_splits=10, test_size=12, max_train_size=None)
# 学習データtrain、検証データvalidの分割
train, valid = [], []
for i, (train_idx, valid_idx) in enumerate(tscv.split(df_air['value'].values)):
# Fold番号と学習データ・検証データのインデックスの表示
print(f'Fold {i}')
print(f' Train: index={train_idx}')
print(f' Test : index={valid_idx}')
# trainにFoldごとの学習データを格納
train.append(df_air.iloc[train_idx])
# validにFoldごとの検証データを格納
valid.append(df_air.iloc[valid_idx])
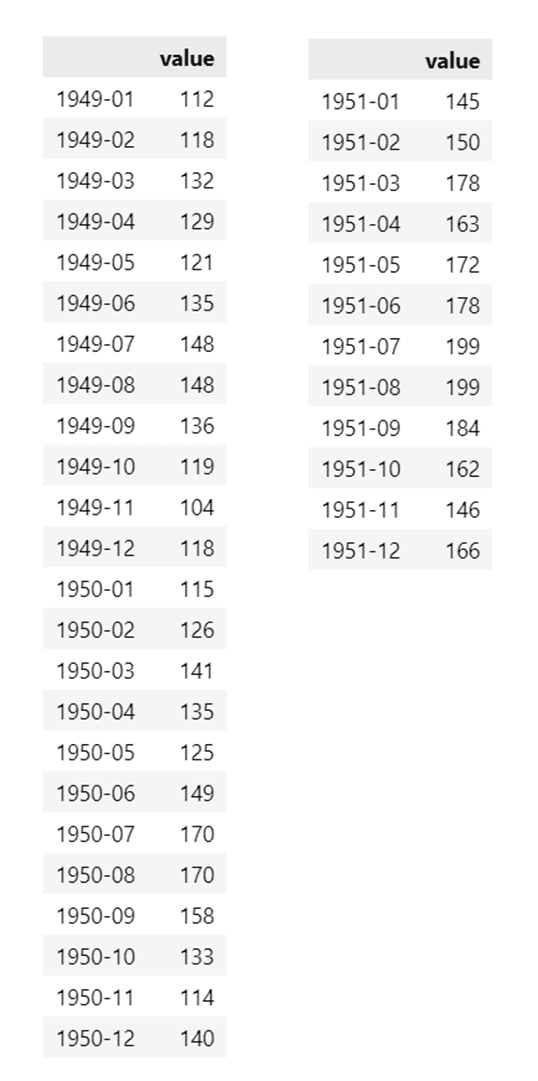
# Fold0の学習データ・検証データを表示
n_fold = 0
display(train[n_fold])
display(valid[n_fold])【補足】TimeSeriesSplit()の引数
n_splits=10
10分割します。test_size=12
検証データに含める期間は12です。max_train_size=None
学習データは期間制限を付けないで、徐々に追加します。
【実行結果】
分割単位=Foldごとの学習データのインデックスと検証データのインデックスを表示しました。
インデックスの順番が保たれていて、検証データに学習データよりも前の期間が設定されていないことが分かります。

続いてFold0(最初のFold)の学習データ(左)と検証データ(右)です。
③ 時系列を考慮した交差検証のデータ分割:学習データを24か月固定にする
TimeSeriesSplit()の引数max_train_size=24とし、学習データの期間を24か月固定にします。
### 時系列を考慮した交差検証のデータ分割 (2)学習データを24か月固定にする方法
# 時系列CVのインスタンス生成 10分割、検証データ12か月、学習データ24か月
tscv = TimeSeriesSplit(n_splits=10, test_size=12, max_train_size=24)
# 学習データtrain、検証データvalidの分割
train, valid = [], []
for i, (train_idx, valid_idx) in enumerate(tscv.split(df_air['value'].values)):
# Fold番号と学習データ・検証データのインデックスの表示
print(f'Fold {i}')
print(f' Train: index={train_idx}')
print(f' Test : index={valid_idx}')
# trainにFoldごとの学習データを格納
train.append(df_air.iloc[train_idx])
# validにFoldごとの検証データを格納
valid.append(df_air.iloc[valid_idx])
# Fold9の学習データ・検証データを表示
n_fold = 9
display(train[n_fold])
display(valid[n_fold])【実行結果】
分割単位=Foldごとの学習データのインデックスと検証データのインデックスを表示しました。
学習データのインデックスはどのFoldも「24」個であることが分かります。

続いてFold9(最終Fold)の学習データ(左)と検証データ(右)です。
検証データは、データセットの最後の12か月を利用していることが分かります。

以上で終了です。
お疲れ様でした。

第5章 へ続く
■次回の取り組みテーマ
2つの時系列データの類似度指標である「相互相関」「移動相関」「動的時間伸縮」(DTW)を実践します。
次の記事
前の記事
目次
ブログの紹介
note で4つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
2.実験!たのしいベイズモデリングをPyMC Ver.5で
書籍「たのしいベイズモデリング」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learn と PyTorch の教科書です。
よかったらぜひ、お試しくださいませ。
4.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Python のコラムを不定期に綴っています。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
最後までお読みいただきまして、ありがとうございました。
この記事が参加している募集
この記事が気に入ったらサポートをしてみませんか?
