「数値シミュレーションで読み解く統計のしくみ」をPythonで写経～第２章2.3「関数を作る」

2024年6月29日 11:52

第２章「プログラミングの基礎」

書籍の著者　小杉考司先生、紀ノ定保礼先生、清水裕士先生

この記事は、テキスト「数値シミュレーションで読み解く統計のしくみ」第２章「プログラミングの基礎」2.3節「関数を作る」の Python写経活動 を取り扱います。

前回からの３記事はシミュレーションの準備体操にあたります。
R の基本的なプログラム記法はざっくり Python の記法と近いです。
コードの文字の細部をなぞって、R と Python の両方に接近してみましょう！
ではテキストを開いて準備体操の旅に出発です🚀

はじめに

テキスト「数値シミュレーションで読み解く統計のしくみ」のご紹介

このシリーズは書籍「数値シミュレーションで読み解く統計のしくみ〜Rでためしてわかる心理統計」（技術評論社、「テキスト」と呼びます）の Python写経です。

テキストは、2023年9月に発売され、副題「Rでためしてわかる心理統計」のとおり、統計処理に定評のある R の具体的なコードを用いて、心理統計の理解に役立つ数値シミュレーションを実践する素晴らしい書籍です。

引用表記

この記事は、出典に記載の書籍に掲載された文章及びコードを引用し、適宜、掲載文章とコードを改変して書いています。
【出典】
「数値シミュレーションで読み解く統計のしくみ〜Rでためしてわかる心理統計」初版第１刷、著者小杉考司・紀ノ定保礼・清水裕士、技術評論社

記事中のイラストは、「かわいいフリー素材集いらすとや」さんのイラストをお借りしています。
ありがとうございます！

2.3 関数を作る

テキストはシミュレーションの基礎になる「Rによるプログラミング」に慣れることを目標にして、初歩的なコードを R で書いています。

この記事は Jupyter Notebook 形式（拡張子 .ipynb）でPythonコードを書きます。
今回取り組む R のコード・構文は Python とよく似ています。

直近で利用するライブラリをインポートします。

### インポート

# 数値計算
import numpy as np

# 確率・統計
import scipy.stats as stats

# 回帰分析
import statsmodels.formula.api as smf

2.3.1 関数とは

関数は「①INPUT → ②処理→ ③OUTPUT」の②処理を一言で使えるようにするプログラムの１形態であり、「①INPUT：引数 → ②処理：関数本体→ ③OUTPUT：戻り値等」となるようにコードを作る感じです。

便利な関数は、Python 本体またはライブラリで提供されています。

テキストにならって平方根の計算をします。
numpyのsqrt関数を使って、16の平方根を計算します。
引数は「16」、関数本体はsqrt()、戻り値は16の平方根となるでしょう。

### 28ページ 平方根
np.sqrt(16)

【実行結果】
戻り値 4 が表示されました。

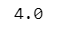
「sqrt()」の内側には平方根を計算するロジックが書かれていると思います。

続いてテキストと類似する回帰分析です。
statsmodelsライブラリの最小二乗法olsを使います。

あやめデータセットをirisに読み込んでおきます。

### 26ページ statamodelsをインポートしてirisデータを取得
from statsmodels.datasets import get_rdataset
iris = get_rdataset(dataname='iris', package='datasets').data
iris = iris.set_axis([x.replace('.', '_') for x in iris.columns], axis=1)

回帰分析を実行します。

### 28ページ 回帰分析
smf.ols('Sepal_Length ~ Petal_Length', data=iris).fit().params

【実行結果】

実はstatsmodelsのolsは関数ではなさそうです。

Pythonで回帰分析を行える関数には scipy.statsライブラリの linregress があります。
単回帰を行う関数です。

### 28ページ scipyで回帰分析

# 説明変数、目的変数の準備
x = iris['Petal_Length'].values
y = iris['Sepal_Length'].values

# 回帰分析の実施 scipy.statsのlinregress関数を利用
result = stats.linregress(x=x, y=y)

# 切片と傾きの表示
print('intercept: ', result.intercept)
print('slope    : ', result.slope)

【実行結果】

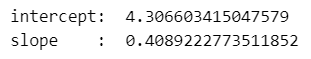
次のコードに注目します。

result = stats.linregress(x=x, y=y)

linregress が関数名、カッコ内の引数には説明変数 x と目的変数 y を与えています。
この計算結果＝戻り値は result に格納されます。
「linregress()」の内側には最小二乗法で単回帰を実施するロジックが書かれていることでしょう。

2.3.2 自作関数を作ってみよう

先程までは「既製服」の関数を「使って」みました。
テキストは関数を「作って」みるフェーズに突入します。

テキストにならって与えられた変数の値に＋２して返す関数を作成します。

### 29ページ def 関数名(引数): で始まり、字下げ（インデント）で処理を書く
def add2(x):
    tmp = x + 2
    return tmp

【実行結果】なし

「def 関数名( 引数1, … ):」ではじまります。
２行目以降は、インデント（字下げ）をして処理コードを書きます。
結果の値を返す（戻り値がある）場合には、「return 戻り値」を書きます。

add2関数を「使って」みましょう。

### 30ページ add2関数の実行
add2(x=4)

【実行結果】
引数で与えた 4 に＋２をして、6 が返ってきました。

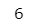
関数の外からadd関数内の変数 tmp にアクセスしてみます。

### 30ページ 関数内の変数の表示を試みる
tmp

【実行結果】
add関数のtmpにアクセスできませんでした。

続いてテキストは addX 関数を作成して「関数外の変数の読み込み」と「関数内の同名変数の更新」に取り組みます。
私が知らないだけかもしれませんが、pythonでは簡単に実装できない感じです。

### 31ページ addX関数の定義
tmp2 = 3
def addX(x):
    tmp = x + 2 + tmp2    # 関数の外の変数の値を読み込むことはできる
    tmp2 = tmp2 + 7       # 関数の外の変数を更新できない この行を実行するとエラー
    return tmp

【実行結果】なし

addX関数を使ってみます。

### 31ページ addX関数の実行
addX(1)

【実行結果】
エラーになりました。

ちなみに関数の外の変数に更新アクセスできるようにする方法はあります。
「global 外の変数名」とします。

### 31ページ addX関数の定義 関数の外の変数にアクセス
tmp2 = 3
def addX(x):
    global tmp2         # 関数の外の変数tmp2を更新可能にする
    tmp = x + 2 + tmp2
    tmp2 = tmp2 + 7     # 関数の外のtmp2を上書きする
    return tmp

【実行結果】なし

addX関数を実行します。

### 31ページ addX関数の実行
addX(1)

【実行結果】
エラーは発生せず、$${1+2+3}$$の計算結果を表示できました。

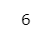
関数の外のtmp2を確認します。

### 31ページ ※関数内のtmp2 = ...で上書きされてしまった
tmp2

【実行結果】
上書きされてしまいました。

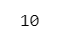
2.3.3 デフォルトの値

関数の引数にデフォルト値、つまり、関数利用時に「引数の値を指定しない」場合に補完する値を設定できます。
テキストの例は、引数 y にデフォルト値 2 を設定しています。

### 32ページ addX2関数の定義と実行
def addX2(x, y=2):
    tmp = x + y
    return tmp

addX2(2, 4)

【実行結果】なし

引数 y に値を設定しないで、addX2関数を実行します。

### 32ページ addX2関数の実行
addX2(2)

【実行結果】
yのデフォルトの値 2 が使われました。

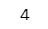
2.3.4 複数の戻り値

return に複数の変数を設定すると、複数の計算結果を戻すことができます。
引数で受けた２つの変数の四則演算結果を返します。

### 33ページ 四則演算関数の定義
def calcs(x, y):
    tmp1 = x + y
    tmp2 = x - y
    tmp3 = x * y
    tmp4 = x / y
    return dict(plus=tmp1, minus=tmp2, multiply=tmp3, divide=tmp4)

【実行結果】なし

関数を実行します。
戻り値を変数「result」で受けて、掛け算結果だけを表示します。

### 34ページ 四則演算関数の実行
## 結果全体をオブジェクトで受け取る
result = calcs(2, 4)
## 掛け算の結果だけ表示
result['multiply']

【実行結果】

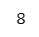
pythonでよく見かける関数の戻り値の方法でcalcs2関数を作ってみました。

### 四則演算関数の定義, 戻り値は辞書はない
def calcs2(x, y):
    tmp1 = x + y
    tmp2 = x - y
    tmp3 = x * y
    tmp4 = x / y
    return tmp1, tmp2, tmp3, tmp4  # 変数を並べる

cals2関数の戻り値の型を確認します。

### 関数の戻り値の型を確認
result = calcs2(2, 4)
type(result)

【実行結果】
タプル型に４つの変数が格納されて戻り値が構成されています。

関数使用の際、次のコードのように戻り値を個々の変数に展開して受け取ることもできます。
アンパックと呼ばれます。
足し算、引き算、掛け算、割り算の４つの変数で受け取って、掛け算のみを表示します。

### 戻り値をアンパックで受け取る
tasu, hiku, kakeru, waru = calcs2(2, 4)
kakeru

【実行結果】

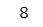
コラム Rによるプロット

テキスト掲載のプロットのケースを python の matplotlib.pyplot で実施してみます。

追加インポートです。

### 追加インポート
import matplotlib.pyplot as plt

■ ２次元データによる直線の描画
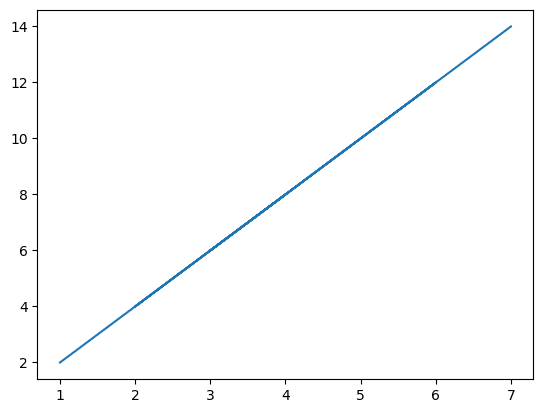
横軸 x と縦軸 y （xの2倍）の値を作成して、線グラフを描画します。
「plt.plot(横軸の値, 縦軸の値)」でプロットできます。

### 34ページ 横軸x, 縦軸y
x = np.array([1, 3, 6, 2, 4, 3, 7])   # 掛け算が可能なnumpy配列を使用
y = x * 2
plt.plot(x, y);

【実行例】

■ １つの変数だけを描画
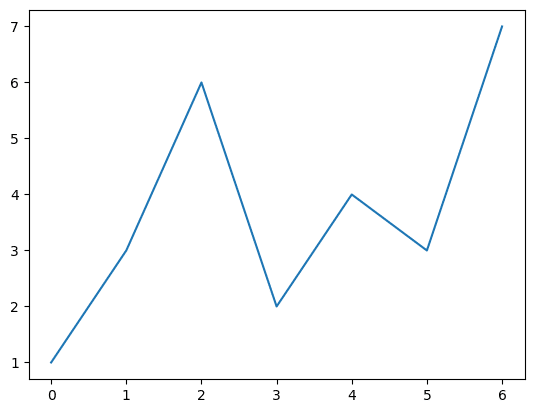
続いて、x だけを指定しての描画です。
x の値は縦軸に反映されます。
横軸には x のインデックス相当（ 0 からの連番）が設定されます。

### 34ページ xのみ
plt.plot(x);

【実行結果】

テキストは続いて、R のオプション type で６種類のグラフを描画しています。
matplotlib には type オプションに相当する単一の指定はなさそうです。
別の設定で６種類のグラフを描きましょう。

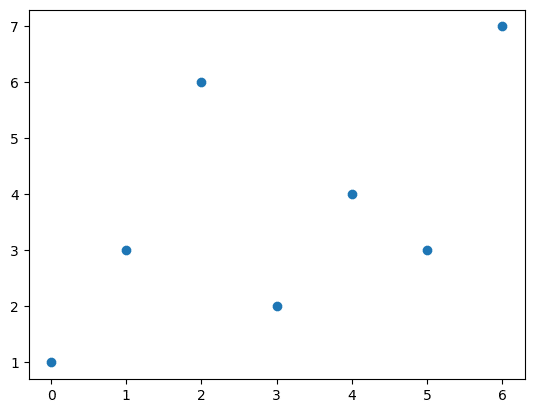
■ １種類目 type='p'相当

### 35ページ type='p'相当
plt.plot(x, 'o');

【実行結果】

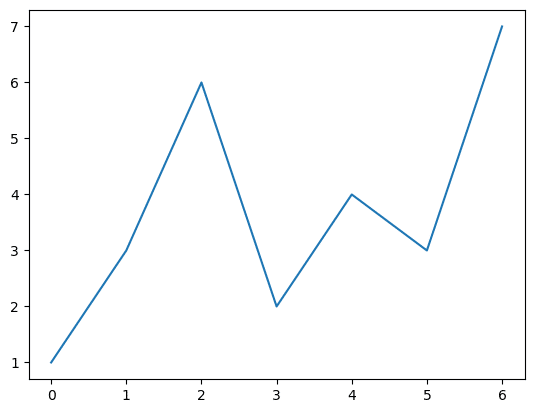
■ ２種類目 type='l'相当

### 35ページ type='l'相当
plt.plot(x);

【実行結果】

■ ３種類目 type='b'相当

### 35ページ type='b'相当
plt.plot(x, '-o');

【実行結果】

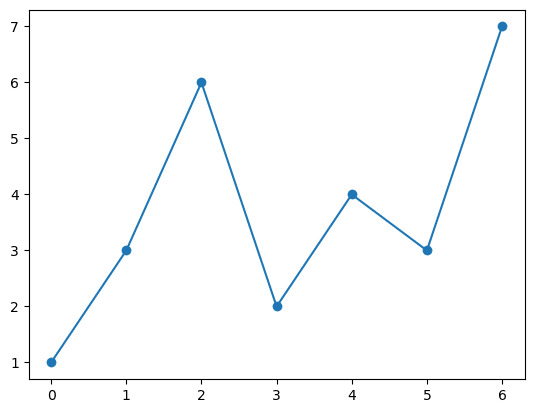
■ ４種類目 type='c'相当

### 35ページ type='c'相当
plt.plot(x, '-o', mfc='white', mec='white');

【実行結果】

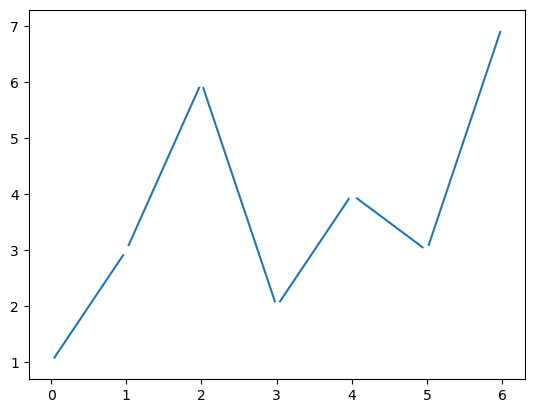
■ ５種類目 type='h'相当
matplotlib の hist を使ってヒストグラムを描画します。

### 35ページ type='h'相当
plt.hist(x);

【実行結果】

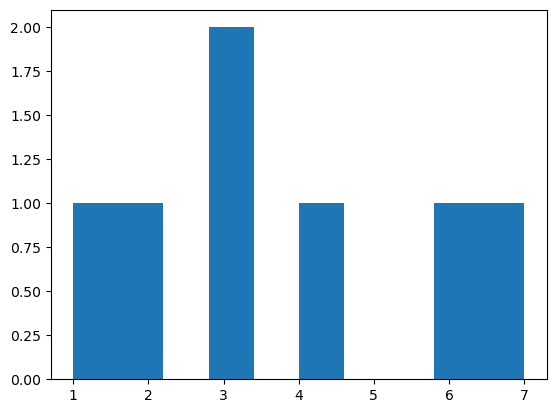
■ ６種類目 type='s'相当
同じく matplotlib の hist を使ってヒストグラムを描画します。

### 35ページ type='s'相当
plt.hist(x, histtype='step');

【実行結果】

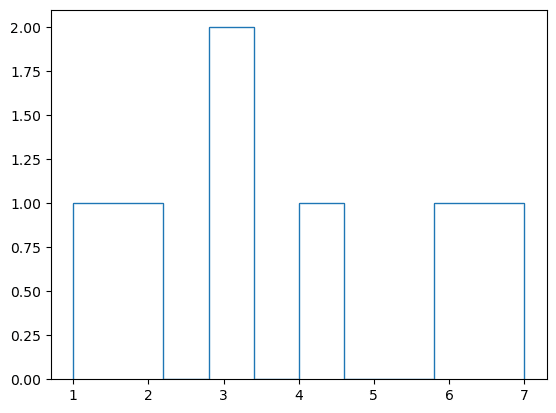
■ 点の形
R の pch オプションのように点の形を変えてみます。
（他にも方法があると思います）

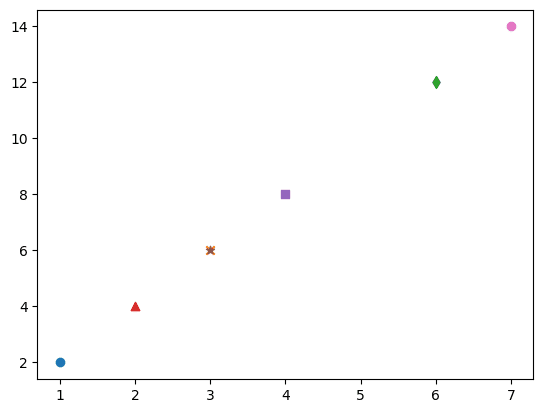
### 35ページ pch=5 相当
markers = np.tile(['o', 'x', 'd', '^', 's', '*'], len(x))
for xval, yval, marker in zip(x, y, markers):
    plt.scatter(xval, yval, marker=marker);

【実行結果】
点の色も変わりました。

■ 点の色
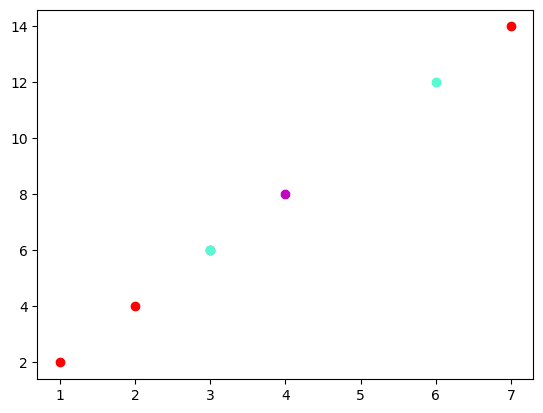
R の col オプションのように点の色を変えてみます。
（他にも方法があると思います）

### 35ページ col= 相当
colors = np.tile(['red', 'm', '#58FAD0'], len(x))
for xval, yval, color in zip(x, y, colors):
    plt.scatter(xval, yval, color=color);

【実行結果】

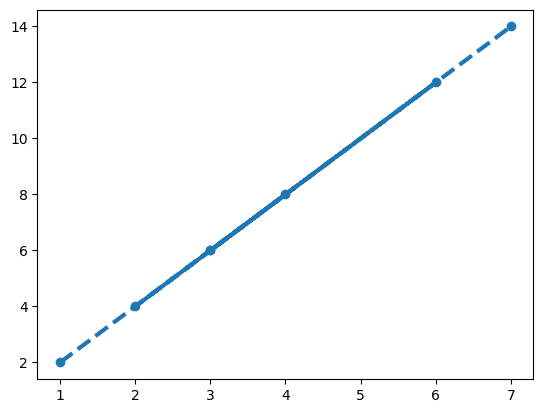
■ 線の種類、太さ
点、線の種類を '--o' でまとめて指定しました。
線の太さは linewidth （省略形 lw）で指定します。

### 35ページ type='b', ity='2', lwd='3'相当
plt.plot(x, y, '--o', linewidth=3);

【実行結果】

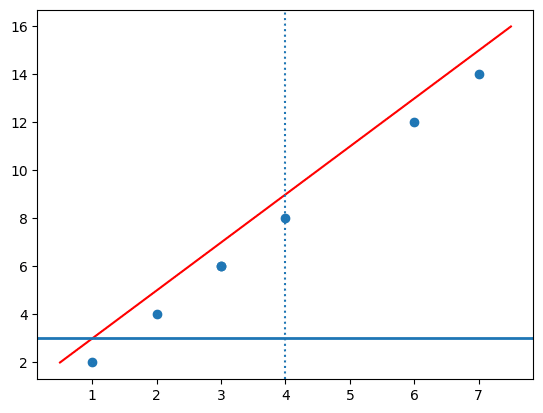
■ さまざまな直線
直線を書き足します。
水平線、垂直線は axhline、axvline で割と簡単に引けます。
切片と傾きを指定する直線描画方法は分からなかったので、xval にx軸の値を設定し、「1 + 2 * x_val」で切片 1 、傾き 2 （x_valの値に対する傾き）を指定しました。

### 35ページ 直線を書き足す

# 点を描画
plt.plot(x, y, 'o');
# 切片1・傾き2の直線を描画
xval = np.linspace(x.min()-0.5, x.max()+0.5, 2)
plt.plot(xval, 1 + 2*xval, color='red')
# 水平線を描画
plt.axhline(3, linewidth=2)
# 垂直点線を描画
plt.axvline(4, linestyle=':');

【実行結果】

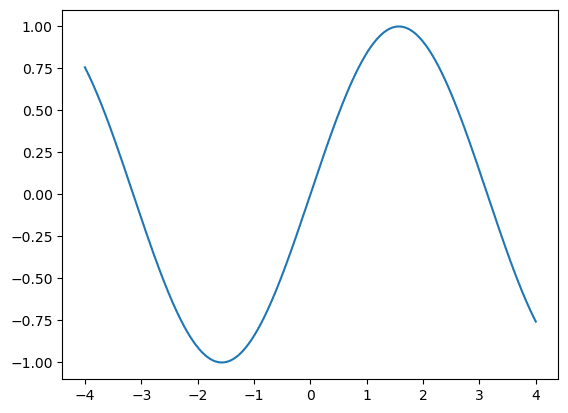
■ 曲線：sin 関数
曲線の引き方はよく分かっていません。
x 軸の値の間隔をとても小さくすることで、ギザギザ感の少ない滑らかな疑似曲線を描画します。
次のコードでは、x 軸の値の間隔をほぼ 0.008 にし、x 軸の値に対応する y 軸の sin関数を値を描画します。

### 35ページ 曲線　三角関数
# x軸の値の設定
xval = np.linspace(-4, 4, 1001)
# 描画
plt.plot(xval, np.sin(xval));

【実行結果】

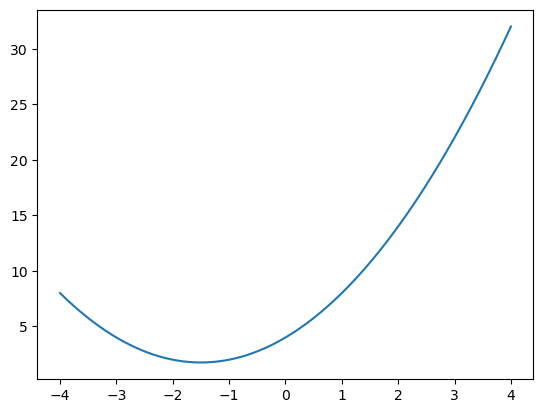
■ 曲線：２次関数
自作関数で定義した２次関数の描画も、上記の sin関数と同様の描画指定をしています。

### 35ページ 曲線　自作関数 xvalはx軸の値

# 自作関数の定義
def myFunc(x):
    return x**2 + 3*x + 4

# x軸の値の設定
xval = np.linspace(-4, 4, 1001)
# 描画
plt.plot(xval, myFunc(xval));

【実行結果】

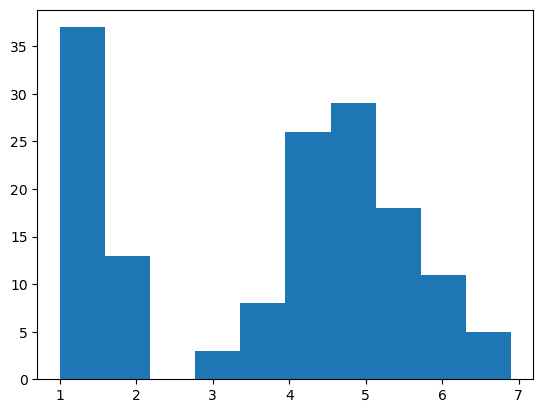
■ あやめデータセットのヒストグラム１
2.3.1 節で読み込んだあやめデータセット iris を用いて、変数 Petal_Length のヒストグラムを描画します。

### 36ページ ヒストグラムの描画
plt.hist(iris['Petal_Length']);

【実行結果】

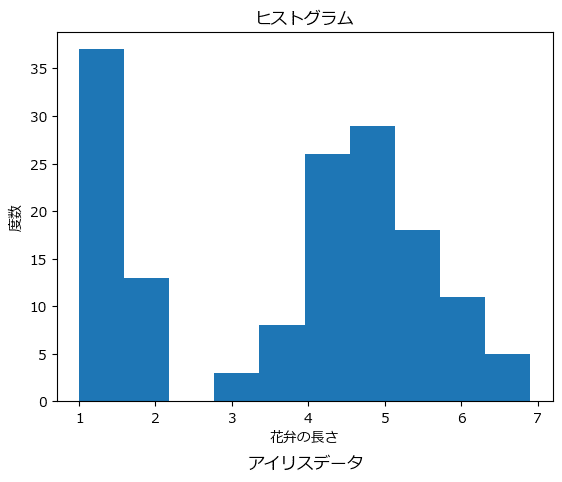
■ あやめデータセットのヒストグラム２
グラフにタイトル、ｘ軸ラベル、ｙ軸ラベルを表示します。
タイトルの指定は plt.title()、ｘ軸ラベルの指定は plt.xlabel()、ｙ軸ラベルの指定はplt.ylabel() で行っています。

### 36ページ ヒストグラムの描画

# 日本語フォントの設定
plt.rcParams['font.family'] = 'Meiryo'

# ヒストグラムの描画
plt.hist(iris['Petal_Length'])
# タイトル、x軸ラベル、y軸ラベルの設定 # subは無い
plt.title('ヒストグラム')
plt.xlabel('花弁の長さ')
plt.ylabel('度数')

# subライクな表示の再現
plt.text(x=3.2, y=-7, s='アイリスデータ', fontsize=12);

【実行結果】

今回の写経は以上です。

シリーズの記事

次の記事

前の記事

ブログの紹介

note で７つのシリーズ記事を書いています。
ぜひ覗いていってくださいね！

１．のんびり統計

統計検定２級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定２級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。

２．実験！たのしいベイズモデリング１＆２をPyMC Ver.5で

書籍「たのしいベイズモデリング」・「たのしいベイズモデリング２」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルはＲ言語＋Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう！

３．実験！岩波データサイエンス1のベイズモデリングをPyMC Ver.5で

書籍「実験！岩波データサイエンスvol.1」の４人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう！

４．楽しい写経ベイズ・Python等

ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀

５．RとStanではじめる心理学のための時系列分析入門を PythonとPyMC Ver.5 で

書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん！
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。

６．データサイエンスっぽいことを綴る

統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。

７．Python機械学習プログラミング実践記

書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。

最後までお読みいただきまして、ありがとうございました。

「数値シミュレーションで読み解く統計のしくみ」をPythonで写経 ～ 第２章2.3「関数を作る」

第２章「プログラミングの基礎」

はじめに

テキスト「数値シミュレーションで読み解く統計のしくみ」のご紹介

引用表記

2.3 関数を作る

2.3.1 関数とは

2.3.2 自作関数を作ってみよう

2.3.3 デフォルトの値

2.3.4 複数の戻り値

コラム Rによるプロット

シリーズの記事

ブログの紹介

いいなと思ったら応援しよう！

「数値シミュレーションで読み解く統計のしくみ」をPythonで写経～第２章2.3「関数を作る」