
4-3 条件付き期待値 ~ 確率変数・期待値・幾何分布を巡る
今回の統計トピック
幾何分布を利用して、当たりが出るまでのくじ引き回数の期待値を計算します。
確率分布と期待値の概念に触れてから、幾何分布を眺めますよっ!
公式問題集の準備
「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください!
「知る」「実践する」の章で、のんびり統計をお楽しみください!
問題を解く
📘公式問題集のカテゴリ
確率の分野
問3 条件付き期待値(くじ引き)
試験実施年月
調査中
問題
公式問題集をご参照ください。
解き方
題意
成功確率$${1/10}$$の幾何分布の期待値を求めます。
幾何分布
当たりの確率$${p}$$のくじを初めて当たりが出るまで引き続けるとき、くじを引く回数$${X}$$の確率分布が幾何分布です。
引いたくじを戻すので当たりの確率は一定です。

幾何分布の期待値$${E[X]}$$は$${1/p}$$です。
問題文より、当たりの確率は$${p=1/10}$$です。
期待値$${E[X]=1/p=1/(1/10)=10}$$なので、答えは 10回 です。
幾何分布には無記憶性の性質があるので、すでに5回連続で外れているという過去の結果は、将来の結果に影響を及ぼしません。
リセットなのです。
毎回、いまから当たりが出るまでにくじを引く回数の期待値は 10回 です。

解答
② 10回 です。
難易度 ふつう
・知識:幾何分布
・計算力:数式組み立て(低)
・時間目安:1分
知る
おしながき
公式問題集の問題に接近してみましょう!
今回は、確率変数、期待値に寄り道してから幾何分布を進みます!
期待値
📕公式テキスト:2.5 期待値と分散(67ページ~)
確率変数と確率
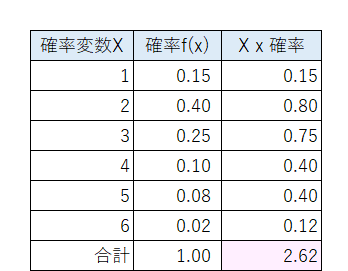
確率変数$${X}$$が1のときの確率が0.15、2のときの確率が0.40・・・のように、確率変数と確率の対応関係を「確率分布」と呼びます。
グラフに表すと、横軸が確率変数$${X}$$、縦軸が確率$${P(X)}$$です。
この例は、確率変数$${X}$$の値が1~6までの飛び飛びの値を取るので、離散型です。

離散型の確率変数$${X}$$の値が$${x_i}$$のとき、確率は$${P(X=x_1)=f(x_i)}$$と表すことができます。
$${P(X=x_1)}$$は確率、$${f(x_i)}$$は確率質量関数です。
離散型の確率変数$${X}$$が1のときの確率は$${P(X=1)=f(1)}$$であり、0.15なので、$${P(X=1)=f(1)=0.15}$$です。
確率変数$${X}$$が$${x_i}$$以下のときの確率は$${P(X \leq x_i)=F(x_i)}$$と表すことができます。
$${F(x_i)}$$は累積分布関数です。
確率変数$${X}$$が4以下のときの確率は$${P(X \leq 4)=F(4)}$$と表し、0.9なので、$${P(X \leq 4)=F(4)=0.9}$$です。
期待値
次の式は、離散型の確率変数$${X}$$の期待値$${E[X]}$$の定義です。
期待値は平均値$${\mu}$$のことです。
$$
E[X]=\displaystyle \sum_i x_i f(x_i)=\mu
$$
確率変数$${X}$$の値$${x_i}$$と確率質量関数$${f(x_i)}$$を掛けて合計します。
上の図表の期待値$${E[X]}$$は 2.62 です。
各行の確率変数$${X}$$と確率$${f(x)}$$を掛けた値の縦計です。
コインの表/裏の期待値
表が1、裏が0の値を持つ確率変数$${X}$$があります。
確率$${P(X=1:表)=P(X=0:裏)=0.5}$$です。
期待値$${E[X]}$$は$${1\times0.5+0\times0.5=0.5}$$です。

サイコロの目の期待値
サイコロの目1から6の値を持つ確率変数$${X}$$があります。
確率$${P(X=1)=P(X=2)=P(X=3)=P(X=4)=P(X=5)=P(X=6)=1/6}$$です。
期待値$${E[X]}$$は$${1\times1/6+2\times1/6+3\times1/6+4\times1/6+5\times1/6+6\times1/6=3.5}$$です。

幾何分布
📕公式テキスト:2.7.4 幾何分布(75ページ~)
成功の確率が$${p}$$であるベルヌーイ試行を初めて成功するまで繰り返した時の試行回数$${X}$$の確率分布を幾何分布(geometric distribution)という。
概要
コインの表が出るまで何回かかるか、サイコロの1の目が出るまで何回かかるか、などの確率を取り扱うのが「幾何分布」です。
確率を考える
初めて成功する回数を$${x}$$回とすると、それまでの失敗回数は$${x-1}$$回です。
成功の確率を$${p}$$とすると、失敗の確率は$${1-p}$$です。
$${x-1}$$回連続で失敗する確率は$${(1-p)^{x-1}}$$です。
初めて成功する確率は$${p^1=p}$$です。
$${x-1}$$回連続で失敗してその次の回で成功する確率は$${p \times(1-p)^{x-1}}$$です。
幾何分布の確率 $${P(X)}$$
$$
P(X=x) \equiv f(x) = p(1-p)^{x-1}\qquad (x=1,2,\cdots)
$$
幾何分布の分布のイメージ
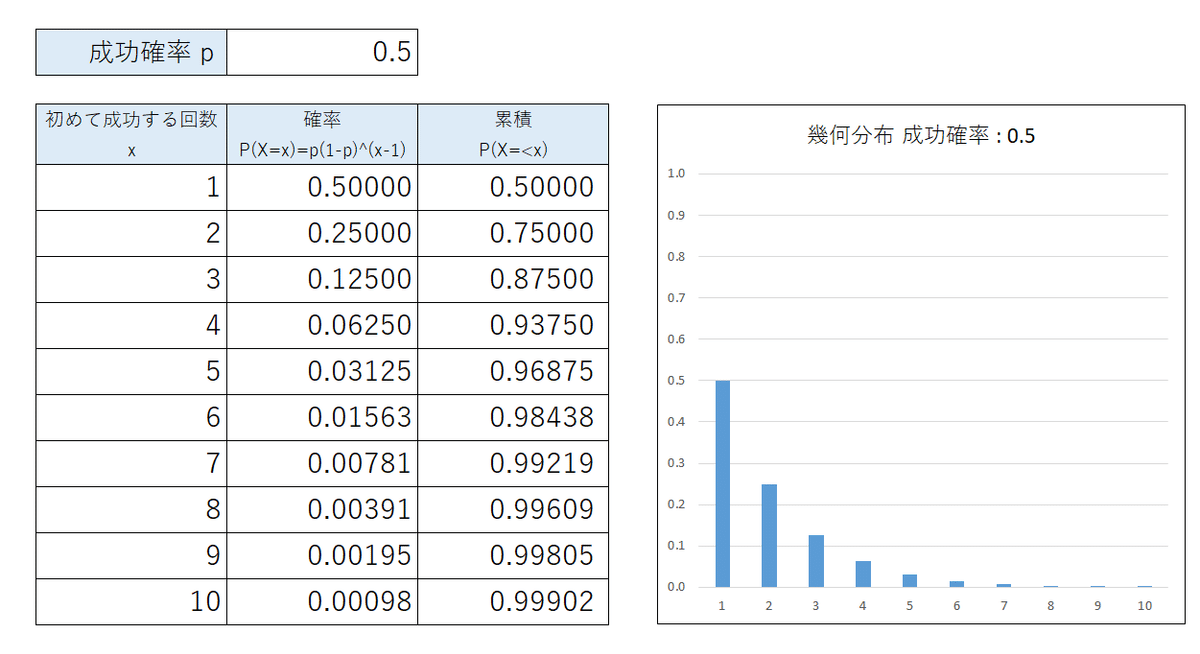
成功確率$${p=0,1, 0.5, 0.9}$$のパターンで分布の様子を確認します。
成功確率が高くなるほど、初めて成功する回数$${X}$$の小さな値の確率が高くなります。


幾何分布の期待値 $${E[X]}$$
幾何分布の期待値の式です。
$$
E[X]=\cfrac{1}{p}
$$
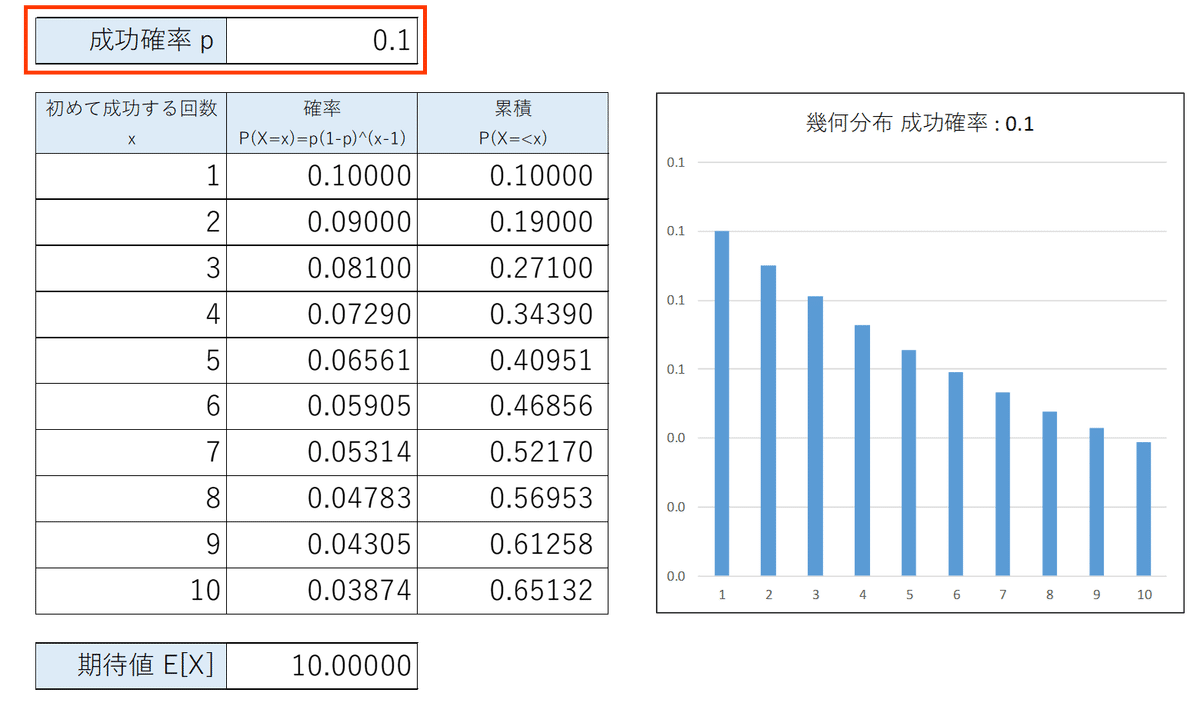
成功確率$${p=1/10}$$の幾何分布の期待値を求めてみましょう。
離散型の確率変数の期待値$${E[X]= \sum_i x_i f(x_i)}$$の公式に、$${i=1, 2, \cdots, 200}$$に限定して確率変数$${X=x_i}$$を当てはめて、期待値の近似値を計算しました。
期待値は 10回 になりました。

コインの表が初めて出るまでにかかる回数(期待値)
コインの表(確率$${p=0.5}$$)が初めて出るまでの試行回数$${X}$$は幾何分布に従います。
幾何分布の期待値は$${E[X]=1/p=1/0.5=2}$$で、2回です。

サイコロの1が初めて出るまでにかかる回数(期待値)
サイコロの1(確率$${p=1/6}$$)が初めて出るまでの試行回数$${X}$$は幾何分布に従います。
幾何分布の期待値は$${E[X]=1/p=1/(1/6)=6}$$で、6回です。

コインの表が初めて出る回数の期待値が2回、サイコロの1が初めて出る回数の期待値が6回。
表裏の2面、サイコロの6面のことを思い出すと、なんだか、当たり前といえば当たり前の結果になりました。
幾何分布の無記憶性
いままで連続で$${n}$$回失敗が続いたときに、さらに、当たりが出るまで$${k}$$回を超える回数がかかるとします。
$${n}$$回失敗した場合に最初の当たりが出るまでの回数が通算$${n+k}$$回を超える確率と、いまからくじ引きを開始して最初の当たりが出るまでの回数が$${k}$$回を超える確率が等しいのです。
つまり、今までに失敗した$${n}$$回の経験に関係なく確率が決まるのです。
式で示すと次のようになります。
$$
P(X>n+k \mid X>n) = P(X>k)
$$

以上、確率変数、確率、期待値、幾何分布を眺めました。
公式のまとめ
離散型の確率変数$${\boldsymbol{X}}$$の期待値
$${E[X]=\displaystyle \sum_i x_i f(x_i)=\mu}$$
幾何分布の確率質量関数
$${P(X=x) \equiv f(x) = p(1-p)^{x-1}\qquad (x=1,2,\cdots)}$$
幾何分布の期待値
$${E[X]=\cfrac{1}{p}}$$
実践する
幾何分布を可視化して特徴を確認してみよう
「知る」の「幾何分布の分布のイメージ」の表とグラフを利用して、さまざまな成功確率を設定して、幾何分布の形状を確認しましょう。
EXCELファイルをダウンロードして、「成功確率p」に $${ 0 < p < 1 }$$の値を設定して、シミュレーションを実施します。
EXCELファイルのダウンロード
こちらのリンクからEXCELファイルをダウンロードできます。
電卓・手作業で作成してみよう!
今回はお休みです。
EXCELで作成してみよう!
上述の「幾何分布を可視化して特徴を確認してみよう」をEXCELを用いて実践しましょう!
ちなみに情報です。
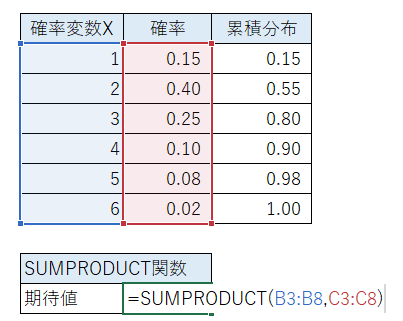
■期待値を計算できる関数
期待値は「確率変数 × 確率」の合計でした。
SUMPRODUCT関数を利用して期待値の計算ができます。
この関数は、引数の「範囲1:確率変数」と「範囲2:確率」のペアを掛け算して、合計値を返してくれます。
ですので、期待値の計算に使えるのです!
EXCELサンプルファイルのダウンロード
上述の「EXCELファイルのダウンロード」よりダウンロードしてください。
Pythonで作成してみよう!
プログラムコードを読んで、データを流したりデータを変えてみたりして、データを追いかけることで、作表ロジックを把握する方法も効果的でしょう。
サンプルコードを揃えておけば、類似する作表作業を自動化して素早く結果を得ることができます。
今回は、幾何分布の図表の作成に取り組みます。
計算過程を明示する目的で、scipy.stats.geom の幾何分布機能を利用せず、計算式を定義しています。
(Pythonのサンプルファイルにscipy.stats.geomの使用例を含めています)
①ライブラリのインポート
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'MS Gothic'
%matplotlib inline②幾何分布の期待値・分散・標準偏差を計算する関数
成功確率$${p}$$と小数点丸め位置$${r}$$を引数で受け取り、次の計算を行ってリストで返します。
期待値$${E[X]=\cfrac{1}{p}}$$
分散$${V[X]=\cfrac{1-p}{p^2}}$$
標準偏差$${\sqrt{V[X]}=\cfrac{\sqrt{1-p}}{p}}$$
def geometric_dist_summary(p, r=5):
exp_val = round(1/p, r) # 期待値
var_val = round((1-p)/p**2, r) # 分散
std_val = round((1-p)**(1/2)/p, r) # 標準偏差
return [exp_val, var_val, std_val]③幾何分布の確率を計算する関数
成功確率$${p}$$と試行回数$${x}$$を引数で受け取り、次の計算を行って確率$${P}$$を返します。
確率$${P(X=x)=p(1-p)^{x-1}}$$
def geometric_dist_prob(p, x):
return p*(1-p)**(x-1)④幾何分布の期待値、分散、標準偏差の表示
成功確率$${p}$$の値を設定して実行します。
$${p}$$の値にいろいろな成功確率$${ (0 < p < 1) }$$を設定して、期待値等を確認しましょう。
p = 0.1 # 成功確率
print('期待値 : ', geometric_dist_summary(p)[0])
print('分散 : ', geometric_dist_summary(p)[1])
print('標準偏差: ', geometric_dist_summary(p)[2])
⑤幾何分布のグラフ表示
成功確率$${p}$$と試行回数の最大値$${n}$$を設定して、棒グラフを表示します。
$${p}$$の値にいろいろな成功確率$${ (0 < p < 1) }$$を設定して、また、試行回数の最大値$${n}$$を変えてみて、さまざまな成功確率の幾何分布を可視化しましょう。
# 設定 p:成功確率, n:試行回数Xの最大値
p = 0.1
n = 50
# 幾何分布のプロット
x = np.arange(1, n+1) # 試行回数X
y = geometric_dist_prob(p, x) # 幾何分布の確率P
plt.bar(x, y)
# 期待値のプロット
exp = geometric_dist_summary(p)[0] # 期待値
if exp <= n:
prob = geometric_dist_prob(p, exp) # 期待値の確率
plt.scatter(exp, prob, marker='*', c='red', s=200)
plt.text(exp+n*0.03, prob, f'$E\ [X]$ = {exp:.1f}')
# 修飾
plt.title('幾何分布')
plt.xlabel('初めて成功する回数 $X$')
plt.ylabel('確率 $P(X)$')
# plt.savefig('./bar.png') # グラフ画像ファイルの保存
plt.show()
Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。
おわりに
初めて確率分布に正面から挑みました。
しかもその確率分布は、二項分布や正規分布を飛び越して、幾何分布だったのです!
ちょっと驚き。。。
確率分布は図表、数式、EXCEL、Pythonの話題をバランスよく配置できるテーマなので、書きやすいです。
最後までお読みいただきまして、ありがとうございました。
のんびり統計シリーズの記事
次の記事
前の記事
目次
