8-1 母平均の検定の考え方～統計的仮説検定の流れに身をまかせ～♪

2023年8月16日 11:37

今回の統計トピック

いよいよ統計的仮説検定のテーマに入ります！
統計らしさを感じるテーマだと思います。
今回は、「１標本の母平均の検定」を「母分散既知」と「母分散未知」の２ケースで実施します。
「知る」の章で統計的仮説検定の流れをじっくり味わいましょう！
「実践する」の章で例題を使って統計的仮説検定を実践しましょう！
いざ、統計的仮説検定の旅へ（長丁場になります）。

公式問題集の準備

「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください！
「知る」「実践する」の章で、のんびり統計をお楽しみください！

問題を解く

📘公式問題集のカテゴリ

検定の分野
問1 母平均の検定の考え方（金融資産の日次収益率）

試験実施年月
調査中

問題

公式問題集をご参照ください。

解き方

題意
母平均の検定の際に、母分散$${\sigma^2}$$の既知／未知に応じて定まる「検定統計量の棄却域」を導き出す問題です。

【条件】
・母平均$${=0}$$を帰無仮説とする。
・確率変数$${X_t\ (t=1,2, \cdots ,n)}$$は独立に同一の正規分布$${N(0, \sigma^2)}$$に従うと仮定する。
・標本平均$${\bar{X}=\frac{1}{n} \sum^n_{t=1}X_t}$$は正規分布$${N(0, \sigma^2/n)}$$に従う。
・標本サイズは$${n=21}$$である。

公式問題集の記述を改変

図示します。

記号は、標本平均$${\bar{X}}$$、母分散$${\sigma^2}$$、標本不偏分散$${\hat{\sigma}^2}$$です。

帰無仮説は「母平均＝０」、対立仮説は「母平均≠０」です。

【ケース①母分散既知】

■検定統計量$${Z}$$が従う分布

標本平均$${\bar{X}}$$は、帰無仮説「母平均＝０」の下で「平均０、分散$${\sigma^2/n}$$の正規分布に従う」と仮定されます。
標本平均$${\bar{X}}$$を標準化した$${Z=\bar{X}/\sqrt{\sigma^2/n}}$$は「標準正規分布」に従います。

■有意水準$${5\%}$$の両側検定の棄却域

有意水準$${5\%}$$の両側検定では、検定統計量$${Z}$$が標準正規分布に従うとして、$${Z}$$の絶対値が$${1.96}$$より大きいときに帰無仮説を棄却します。

標準正規分布の確率密度関数を確認しましょう。

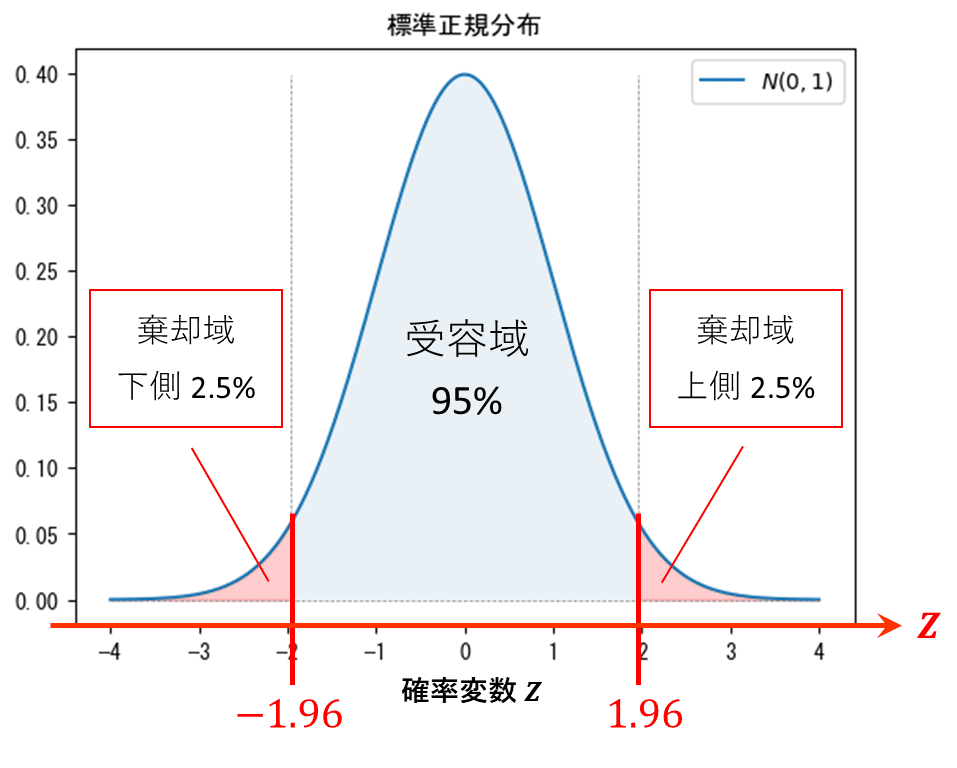
観測値より求めた確率変数$${Z}$$の実現値が$${-1.96}$$以下または$${1.96}$$以上のとき、面積＝確率が合計$${5\%}$$になります。
下の図の赤い棄却域は合計$${5\%}$$です。
これが有意水準$${5\%}$$の棄却域なのです。

選択肢から選ぶ（ア）の解答は$${|Z|>1.96}$$です。

$${1.96}$$の値は、標準正規分布の上側確率表より、有意水準$${5\%}$$の半分に当たる$${2.5\%}$$点の値を取得します。

【ケース②母分散未知】

■検定統計量$${T}$$が従う分布

標本平均$${\bar{X}}$$は、帰無仮説「母平均＝０」の下で「平均０、分散$${\sigma^2/n}$$の正規分布に従う」と仮定されます。
標本平均$${\bar{X}}$$を標準化した$${Z=\bar{X}/\sqrt{\sigma^2/n}}$$は「標準正規分布」に従います。

しかし、母分散$${\sigma^2}$$が未知であるため、検定統計量$${Z}$$の$${\sigma^2}$$を標本不偏分散$${\hat{\sigma}^2}$$に置き換えます。
この置き換え後の検定統計量$${T=\bar{X}/\sqrt{\hat{\sigma}^2/n}}$$は、標本サイズ$${n}$$を用いて、「自由度$${n-1}$$の$${t}$$分布」に従います。

問題では標本サイズが$${21}$$なので、「自由度$${\boldsymbol{20}}$$の$${\boldsymbol{t}}$$分布」に従うことになります。

■有意水準$${5\%}$$の両側検定の棄却域

有意水準$${5\%}$$の両側検定では、検定統計量$${T}$$が自由度$${20}$$の$${t}$$分布に従うとして、$${T}$$の絶対値が$${2.086}$$より大きいときに帰無仮説を棄却します。

自由度$${20}$$の$${t}$$分布の確率密度関数を確認しましょう。

観測値より求めた確率変数$${T}$$の実現値が$${-2.086}$$以下または$${2.086}$$以上のとき、面積＝確率が合計$${5\%}$$になります。
下の図の赤い棄却域は合計$${5\%}$$です。
これが有意水準$${5\%}$$の棄却域なのです。

選択肢から選ぶ（イ）の解答は$${|T|>2.086}$$です。

$${2.086}$$の値は、$${t}$$分布のパーセント点表より、有意水準$${5\%}$$の半分に当たる$${2.5\%}$$点の値を取得します。

【ケース③母分散未知、正規分布近似】

■検定統計量$${T}$$が従う分布

検定統計量$${T=\bar{X}/\sqrt{\hat{\sigma}^2/n}}$$は、標本サイズ$${n}$$を用いて、自由度$${n-1}$$の$${t}$$分布に従います。
ただし、問題文章より、正規分布近似を用いることとしているため、検定統計量$${T}$$は「標準正規分布」に近似的に従うことになります。

■有意水準$${5\%}$$の両側検定の棄却域

ケース①と同様です。
検定統計量$${T}$$が標準正規分布に従うとして、$${T}$$の絶対値が$${1.96}$$より大きいときに帰無仮説を棄却します。

選択肢から選ぶ（ウ）の解答は$${|T|>1.96}$$です。

解答

① です。

難易度　やさしい

・知識：母平均の検定（母分散既知・未知）、標準正規分布の上側確率表、$${t}$$分布のパーセント点表
・計算力：不要
・時間目安：1分

知る

おしながき

公式問題集の問題に接近してみましょう！
今回は、例題に沿って統計的仮説検定の流れを見ていきましょう。

統計的仮説検定

📕公式テキスト：4.2.1 帰無仮説・対立仮説と有意水準（137ページ～）

統計的仮説検定って？

統計的仮説検定でやりたいことは、ざっくり次のような感じです。

実験や調査をした結果、仮説では起きにくい「レアなことが起きた」ので、仮説がおかしいと判断して、仮説を採用しない。

ポイントは、「仮説」「レア度の水準」「起きたことの定量化」「判断」です。

５つのステップ

次の５つのステップで統計的仮説検定をイメージしやすくなると思います！
（個人の感想です）

仮説を設定する～「仮説」
有意水準を設定する～「レア度の水準」
検定統計量・確率分布・棄却域を明確にする
～「起きたことの定量化」（計画）
検定統計量を計算する
～「起きたことの定量化」（実績）
判断する～「判断」

では、例題を手がかりにして統計的仮説検定の体験ツアーに出発です！

例題で統計的仮説検定を体感する

例題
今年の新入社員64人を対象にプログラミングスキルの試験を実施したところ、平均点は75点でした。
昨年までに実施した試験の結果から、この試験の得点は平均70点、標準偏差16点の正規分布に従うことが明らかになっています。
さて、今年の状況を踏まえて、平均点は過去の平均点から変わってしまったのでしょうか？
有意水準5%で検定しましょう。

ステップ１：仮説を設定する

■帰無仮説
まず、反論したい仮説を定めます。
この仮説のことを「帰無仮説」と呼びます。記号$${H_0}$$で表します。
$${H}$$は「仮説：hypothesis」の頭文字です。
例題の帰無仮説は「平均点は過去の平均点70点から変わっていない」です。

■対立仮説
そして、帰無仮説の反対の仮説を設定します。
この反対の仮説を「対立仮説」と呼びます。記号$${H_1}$$で表します。
例題の対立仮説は「平均点は過去の平均点70点から変わっている」です。
気持ち的には対立仮説を応援したい（こちらの仮説を支持したい）ところなのです！

■仮説の定量化
「起きたことの定量化」をしたいので、帰無仮説、対立仮説も定量化します。
例題は「平均」を論点にする「母平均の検定」を取り扱っています。
母平均を$${\mu}$$と表記するとき、帰無仮説と対立仮説は

帰無仮説 $${H_0: \mu=70}$$、対立仮説 $${H_1: \mu \neq 70}$$

となります。

■対立仮説のバリエーション
例題は「平均点が変わっている」ことを対立仮説にするので「$${H_1: \mu \neq 70}$$」としました。
このほかに「平均点が上がっている」「平均点が下がっている」のバリエーションが考えられます。
次のように対立仮説を立てます。

■対立仮説：３つのバリエーション
・平均点が変わっていない　→　$${H_1: \mu \neq 70}$$
・平均点が上がっている　　→　$${H_1: \mu > 70}$$
・平均点が下がっている　　→　$${H_1: \mu < 70}$$

実は対立仮説に現れる$${\neq, >, <}$$の記号は大切です！
記号によって「両側検定」「片側検定」が決まるからです。
詳細はステップ３で。

ステップ２：有意水準を設定する

■有意水準とは？
有意水準は「レア度の水準」です。
統計検定２級では問題文で有意水準１０％、５％、１％等の値を設定しています。
例題では「平均点が70点から変わっていないと主張しようにも、今年の平均点はかけ離れている（レアなことが起きている）ので、主張できない」と判断する有意水準を「５％」にしています。

■レアなことが起きているとは？
では、「かけ離れている５％」ってなんでしょう。
それは、何らかの確率分布に照らして、中心部から外れたところに位置することなのです。

次の図を見てみましょう。
起きたことを定量化した「検定統計量」が従う確率分布を想定します。
検定統計量の計算値が外側の５％に入る場合が「レアなことが起きた」なのです。
滅多に起きない５％のことが起きたのです。

太い赤矢印の線が検定統計量の数直線です。
検定統計量の計算値をこの数直線にプロットするとしましょう。
この計算値がレアの５％に収まるかどうかを、数直線の上に描いた確率分布の「確率」（％）を利用して判断する。こんなイメージです。

■有意水準とリスク：第１種の過誤
ちなみに、有意水準の％を小さくすると、レアはどんどん外側にずれるので、帰無仮説をなかなか不採用にできなくなります。
その分「本当は帰無仮説が正しいのに誤って不採用にするリスク」は減少します。
逆に、有意水準の％を大きくすると、レアはどんどん内側に広がるので、帰無仮説を不採用にしやすくなります。
しかし「本当は帰無仮説が正しいのに誤って不採用にするリスク」が増加します。
「本当は帰無仮説が正しいのに誤って不採用にする（棄却する）リスク」のことを「第１種の過誤」と呼びます。
有意水準は第１種の過誤の確率を表します。
（第１種の過誤は次回記事で取り扱います！）

ステップ３：検定統計量・確率分布・棄却域を明確にする

■明確にすること
標本を得て、標本から「起きたことを定量化」することが、統計的仮説検定の醍醐味でしょう。
標本が従う確率分布と検定の種類（パターン）によって、起きたことを定量化する検定統計量と確率分布が定まり、有意水準を用いて棄却域が定まります。
棄却域は先程の「レア」の領域にあたり、帰無仮説を不採用にする（棄却する）範囲のことです。

例題では次のように設定しています。

・標本が従う確率分布は「平均70、標準偏差16の正規分布」
・検定の種類は「母平均の検定（母分散既知）」
・検定統計量は「$${Z}$$」。$${Z}$$は「標準正規分布」に従います。

■標準正規分布と棄却域
検定統計量$${Z}$$が従う「標準正規分布の確率密度関数」を可視化して「棄却域」を確認します。
棄却域は、赤塗りの部分に該当する横軸の値です。

両側検定を行う場合、分布の「両端」が棄却域になります。
有意水準$${5\%}$$の場合、両端の確率の合計が$${5\%}$$になります。
正規分布は左右対称なので、左側（下側）の$${2.5\%}$$と右側（上側）の$${2.5\%}$$が棄却域です。

■棄却限界値
グラフの赤い垂直点線が「棄却限界値」を示しています。
棄却限界値の外側が棄却域というわけです。
棄却限界値の絶対値は、標準正規分布の上側確率表の上側確率$${2.5\%}$$点で確認します。
棄却限界値の絶対値は$${1.96}$$です。

■検定統計量$${Z}$$と棄却域のまとめ
検定統計量$${Z}$$の計算値と棄却域の関係を整理します。

【棄却域】
次のように棄却域に$${Z}$$の計算値を含む場合、帰無仮説を棄却します。
・棄却限界値$${-1.96}$$よりも小さい場合：$${Z<-1.96}$$
・棄却限界値$${1.96}$$よりも大きい場合：$${Z>1.96}$$

【受容域】
次のように受容域に$${Z}$$の計算値を含む場合、帰無仮説を棄却しません。
・棄却限界値$${-1.96}$$と$${1.96}$$の間の場合：$${-1.96\leq Z \leq 1.96}$$

■両側検定と片側検定
対立仮説の記号（不等号など）によって、両側検定・片側検定における棄却域が定まります。
対立仮説の３つのバリエーションを再掲します。

■対立仮説：３つのバリエーション
①平均点が変わっていない　→　$${H_1: \mu \neq 70}$$
②平均点が上がっている　　→　$${H_1: \mu > 70}$$
③平均点が下がっている　　→　$${H_1: \mu < 70}$$

標準正規分布に沿って３つのバリエーションの「５％の棄却域」を確認しましょう。

①平均点が変わっていない（$${H_1: \mu \neq 70}$$）は「両側検定」です。
今まで見てきた棄却域ですね。

②平均点が上がっている（$${H_1: \mu > 70}$$）は「片側検定」（上側）です。
棄却限界値は$${1.645}$$となり、検定統計量$${Z>1.645}$$のときに帰無仮説を不採用（棄却）にします。

③平均点が下がっている（$${H_1: \mu < 70}$$）は「片側検定」（下側）です。
棄却限界値は$${-1.645}$$となり、検定統計量$${Z<-1.645}$$のときに帰無仮説を不採用（棄却）にします。

■参考情報～統計検定２級の主な「検定の種類」「検定統計量」
統計検定２級の公式テキストに記載されている種類（パターン）を列挙いたします。
これらのパターンと検定統計量の公式を覚えて試験対策しましょう。
なお、いずれのパターンも、「標本が正規分布に従っている、あるいは、正規分布に近似的に従っている」場合の検定です。

【１標本問題】
Ⅰ．母平均の検定
　①母分散既知：標準正規分布、検定統計量$${Z}$$
　②母平均未知：$${t}$$分布、検定統計量$${T}$$
Ⅱ．母分散の検定：$${\chi^2}$$分布、検定統計量$${\chi^2}$$
Ⅲ．母比率の検定：標準正規分布近似、検定統計量$${Z}$$

【２標本問題】
Ⅰ．２つの母平均の差の検定
　①母分散既知：標準正規分布、検定統計量$${Z}$$
　②母分散が未知で等しい：$${t}$$分布、検定統計量$${T}$$
　③母分散が未知で等しいと仮定できない
　：$${t}$$分布、検定統計量$${T}$$（ウェルチの検定）
　④２つの標本に対応がある
　：$${t}$$分布、検定統計量$${T}$$
Ⅱ．２つの母分散の比の検定：$${F}$$分布、検定統計量$${F}$$
Ⅲ．２つの母比率の差の検定：標準正規分布近似、検定統計量$${Z}$$

ステップ４：検定統計量を計算する

標本である「今年の試験の得点データ」から検定統計量$${Z}$$を計算します。
例題の設定条件を振り返ります。

試験の得点を確率変数$${X}$$と表記します。
試験の得点$${X}$$は平均$${\mu＝70}$$、分散$${\sigma^2=16^2}$$の正規分布$${N(70, 16^2)}$$に従っています。
今年の試験は、受験者数（標本サイズ）$${n=64}$$、得点の平均（標本平均）$${\bar{X}=75}$$です。
ちなみに標本平均の分散は$${V[\bar{X}]=\sigma^2/n}$$です。

検定統計量$${Z}$$は標本平均$${\bar{X}}$$を標準化して求めます。
次の標準化の公式を利用しましょう。

【標本平均の標準化～検定統計量$${Z}$$の公式】
$${Z=\cfrac{\bar{X}-\mu}{\sqrt{\sigma^2/n}} }$$

標本平均$${\bar{X}=75}$$、母平均$${\mu=70}$$、母分散$${\sigma^2=16^2}$$、標本サイズ$${n=64}$$を標準化の公式に当てはめます。

$${Z=\cfrac{\bar{X}-\mu}{\sqrt{\sigma^2/n}} =\cfrac{75-70}{\sqrt{16^2/64}}=\cfrac{5}{\sqrt{4}} =\cfrac{5}{2} =2.5 }$$

検定統計量$${\boldsymbol{Z}}$$の計算値は$${\boldsymbol{2.5}}$$です。

ステップ５：判断する

ステップ３で求めた有意水準５％・両側検定の棄却域は$${Z<-1.96, \quad Z>1.96}$$です。

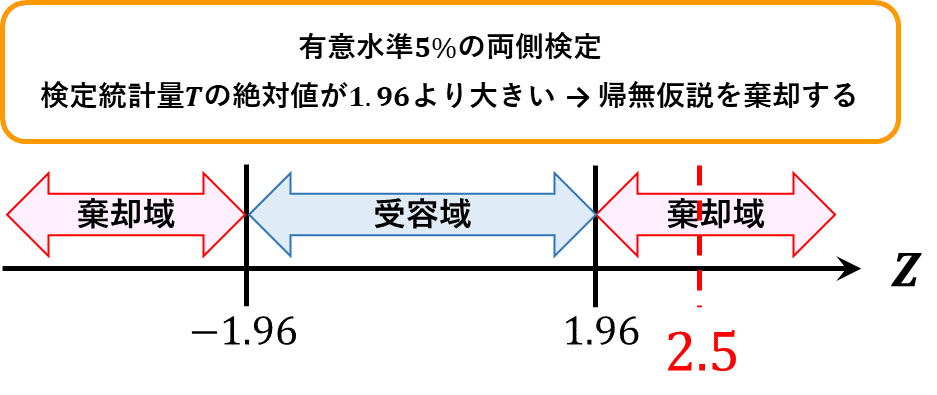
ステップ４で求めた検定統計量$${Z}$$の計算値は$${2.5}$$であり、$${Z>1.96}$$に該当します。

検定統計量の計算結果が棄却域に含まれる場合、「帰無仮説を棄却します」。

「棄却する」ことは、帰無仮説「平均点は過去の平均点70点から変わっていない」を「採用しない」ということです。

結論はこうなります。

有意水準５％で帰無仮説は棄却され、対立仮説「平均点は過去の平均点70点から変わっている」を採択する（受容する）。

■統計的仮説検定の結論で言えること
例題について統計的に言えるのは「今年の試験の平均点は過去の平均点から変化していること」であり、言えるのはこれだけです。
どのくらい変化したかを「例題の検定」では示すことができません。

■検定統計量の計算値が受容域に含まれる場合の結論
検定統計量の計算値が受容域に含まれる場合は帰無仮説を棄却できません。
帰無仮説を棄却しない場合の結論は次のような感じです。

有意水準５％で帰無仮説は棄却されず、対立仮説「平均点は過去の平均点70点から変わっている」とは言えない。

帰無仮説「平均点は過去の平均点70点から変わっていない」を積極的に採択するのではなく、「標本データが対立仮説を支持していない」程度の捉え方をするようです。

ここからは想像上の話です。
今年の新入社員は平均点が75点でした。
そして、例年の平均点70点から変化したことが統計的に明らかになりました。
きっと、今年の新入社員は例年に比べてプログラミング能力が高いのだと想像いたします。

【おまけ】標本平均$${\boldsymbol{\bar{X}}}$$を検定統計量にして母平均の検定を実施

例題の仮定より、得点の平均＝標本平均$${\bar{X}}$$は正規分布に従っています。
そこで、標本平均$${\bar{X}}$$の従う正規分布を確認して、標本平均の値を使って検定してみましょう。

■標本平均が従う正規分布の明確化
まずは、標本平均$${\bar{X}}$$の従う正規分布を求めましょう。

【標本平均の期待値と分散】
標本平均$${\bar{X}}$$の期待値は母平均$${\mu=70}$$です。
標本平均$${\bar{X}}$$の分散は母分散$${\sigma^2}$$と標本サイズ$${n}$$を用いて、$${\sigma^2/n}$$です。
例題の標本平均の分散を計算すると、$${16^2/64=4}$$です。

【得点の平均が従う正規分布】
得点の平均（標本平均）$${\bar{X}}$$は、平均$${\mu=70}$$、分散$${\sigma^2/n=4}$$の正規分布$${N(70,4)}$$に従います。

標本平均$${\bar{X}}$$は正規分布$${N(70, 4)}$$に従うことが分かりました。

■正規分布のプロット
次に正規分布$${N(70, 4)}$$の確率密度関数を可視化して、両側検定の有意水準を示しましょう。

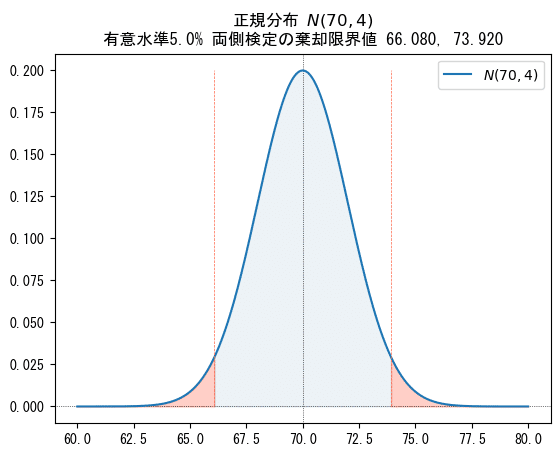
■検定結果は・・・
棄却域は$${\bar{X}<66.08, \bar{X}>73.92}$$です。
この棄却限界値は標準化を施していないので、単位は試験の得点です。
この棄却域に標本平均$${\bar{X}=75}$$を当てはめると、棄却域$${\bar{X}>73.92}$$に含まれます。

やはり、帰無仮説は棄却されるのです！

■標準化した検定統計量$${Z}$$の意義
なぜ標本平均を標準化して検定統計量$${Z}$$にするのでしょう？
おそらく、さまざまな平均・分散の値をもつ正規分布の両側の確率を計算するのが大変だからだと思います。
標準化した「標準正規分布」の場合、検定統計量$${Z}$$の値に対応した確率の表「標準正規分布の上側確率表」から棄却域（確率）を読み取れます。

以上を持ちまして統計的仮説検定ツアーは終点です。
お楽しみいただけたでしょうか？

次のコーナーでは、EXCELとPythonを利用してサクッと母平均の検定を行う方法を検討します。
まだまだ続きますよっ！

実践する

母平均の検定を実行してみよう！

今回は「知る」の章の例題に沿った「試験の得点データ」を用いて、２種類の母平均の検定を実践してみましょう。
EXCELとPythonをミックスして進めてまいります！

利用データ
標本サイズ（データ個数）64、標本平均約75、標本標準偏差（不偏分散の平方根）約16のデータです。

66,53,71,47,36,89,73,85,72,54,57,76,93,54,60,76,67,75,86,66,51,70,39,75,51,63,86,67,56,63,75,83,90,95,80,56,97,84,99,75,75,68,68,68,64,89,94,56,81,98,97,79,85,98,82,61,79,100,94,92,85,90,95,91

CSVファイルのダウンロード
こちらのリンクからCSVファイルをダウンロードできます。

電卓・手作業で作成してみよう！

利用データを用いて、EXCEL・Pythonの実施内容を見つつ、できるところを手作業で実行してみるのはいかがでしょう？

EXCELで作成してみよう！

データ数が多い場合、やはり手作業では非効率になります。
パソコンを利用して、手早く作表できるようになれば、実務活用がしやすくなるでしょう。

母平均の検定（母分散既知）を実施する

計算シートがあります！
例題に沿って、帰無仮説の平均$${＝70}$$、母分散$${＝16^2}$$、有意水準$${5\%}$$、検定方法＝両側検定、で実行しました。

左側の「データ」エリアにデータを設定して、入力パラメータを登録すると、検定統計量$${Z}$$を計算して、母平均の検定（母分散既知）の結果を「判定」エリアに文章表示します。

結果は、「知る」の検討どおり、帰無仮説を棄却して「平均は70点から変わったと言える」になりました。
仮説検定で重要な数値：「検定統計量Z」、「z検定（上側確率）」、「p値」については、後で詳しく説明いたします。

計算式を見ると複雑ですが、やっていることは下の図のように単純です。
統計的な結果が棄却域と受容域のどちらに含まれるかを計算しているのです！

計算シートの見方、計算の仕方

入力パラメータは次のとおりです。

■帰無仮説の平均
・「母集団の平均」などの検定する平均です。
・帰無仮説$${H_0: \mu=\mu_0}$$の$${\mu_0}$$の値です。
■母分散：母集団の分散です。
■有意水準：５％等の値です。
■検定方法
・「両側検定」、「片側検定(上側)」、「片側検定(下側)」から選択します。
・両側検定(上側)は対立仮説$${H_1: \mu \neq \mu_0}$$に対応します。
・片側検定(上側)は対立仮説$${H_1: \mu > \mu_0}$$に対応します。
・片側検定(下側)は対立仮説$${H_1: \mu < \mu_0}$$に対応します。

計算にはEXCELの関数を用いています。
具体的な計算式を列挙いたします。

■標本サイズ（データ件数）
　=COUNT(C5:C1002)
■標本平均
　=AVERAGE(C5:C1002)
■検定統計量Z
　=STANDARDIZE(G12,G5,SQRT(G6/G11))
■z検定（上側確率）
　=Z.TEST(C5:C1002,G5,SQRT(G6))
■p値
　=IF(G8="両側検定",2*MIN(G14,1-G14),IF(G8="片側検定(下側)",1-G14, IF(G8="片側検定(上側)",G14,0)))

特徴的な関数を紹介いたします。

【STANDARDIZE関数】
データの標準化$${Z=(データ値X-平均)/標準偏差}$$を行う関数です。
引数は、STANDARDIZE( データ値, 平均, 標準偏差 )です。

■検定統計量$${Z}$$に活用
STANDARDIZE関数を用いてデータの標本平均を標準化して、検定統計量$${Z}$$を求めました。
検定統計量$${Z}$$の公式を振り返ります。

検定統計量$${Z=\cfrac{\bar{X}-\mu_0}{\sqrt{\sigma^2/n}}=\cfrac{標本平均-帰無仮説の平均}{\sqrt{母分散/標本サイズ}}}$$

公式に合わせて、関数の引数を設定しました。
STANDARDIZE( 標本平均, 帰無仮説の平均, 平方根( 母分散 / 標本サイズ) )

【Z.TEST関数】
標本データを渡すと標準正規分布の上側確率を返す関数です。
引数は、Z.TEST( データの範囲, 母集団の平均, 母集団の標準偏差 )

■検定統計量$${Z}$$の上側確率に活用
Z.TESTを用いて、検定統計量$${Z}$$の上側確率と同じ値を取得しています。
引数の設定は次のとおりです。
Z.TEST( 標本データの範囲, 帰無仮説の平均, 母分散の平方根 )

$${\boldsymbol{p}}$$値とは？

$${p}$$値は確率分布に統計検定量の計算値を当てはめて算出した確率の値です。
帰無仮説を棄却できるかどうかの判断に用いる指標が$${p}$$値なのです！

$${p}$$値が有意水準の値よりも小さい場合に帰無仮説を棄却します。
両側検定、片側検定（上側）、片側検定（下側）によって$${p}$$値の計算方法が変わります。

例題の統計検定量$${Z}$$と標準正規分布を用いて確認します。

■両側検定の$${p値}$$
はじめに両側検定です。図の緑色の面積が$${p}$$値です。

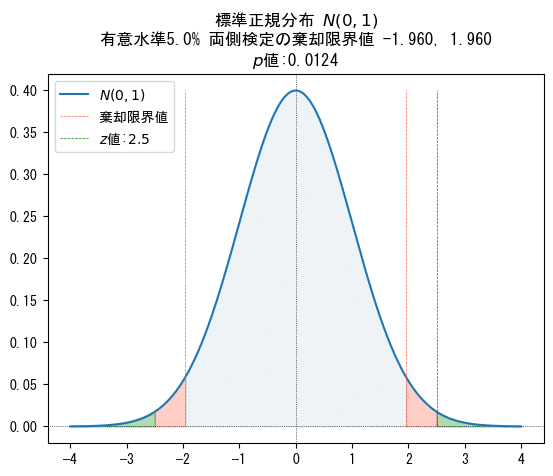
検定統計量$${Z}$$の計算値$${2.5}$$の位置に緑色の垂直点線をプロットしました。
検定統計量$${Z}$$より大きい上側の確率と、左右対称の下側の確率を足すと、両側検定の$${p}$$値$${0.0124}$$になります。
上側確率$${\times 2}$$で求めてもＯＫです。

赤色の棄却域よりも緑色の$${p}$$値が小さいです。
この状態は、有意水準$${5\%}$$よりも$${p}$$値が小さいこと、そして棄却域に含まれることを示しています。
そうです。この状態が帰無仮説を「棄却」できる状態なのです。

■片側検定（上側）の$${p}$$値
対立仮説$${H_1: \mu > \mu_0}$$のように確率分布の上側を見る片側検定です。

検定統計量$${Z}$$の計算値$${2.5}$$より上側の確率$${0.0062}$$が$${p}$$値です。

■片側検定（下側）の$${p}$$値
対立仮説$${H_1: \mu < \mu_0}$$のように確率分布の下側を見る片側検定です。

検定統計量$${Z}$$の計算値$${-2.5}$$より下側の確率$${0.0062}$$が$${p}$$値です。

データやパラメータを変えてオリジナルの検定をしよう！

データ、入力パラメータにさまざまな値を設定して、独自の母平均の検定を試してみましょう。
次の図は、帰無仮説の平均を78.5点にして、有意水準5%の片側検定（下側）を行いました。

帰無仮説「平均は78.5点から変わっていない」（$${H_0: \mu=78.5}$$）
対立仮説「平均は78.5点より小さくなっている」（$${H_1: \mu<78.5}$$）

検定の結果、帰無仮説は棄却され、平均は78.5点より小さくなっていると言えます。

母平均の検定（母分散未知）を実施する

話が変わります。
ここからは、母分散がわからないときの母平均の検定にトライします！
まずは計算シートです。
例題に沿って、帰無仮説の平均$${＝70}$$、有意水準$${5\%}$$、検定方法＝両側検定、で実行しました。

こちらの検定も、帰無仮説を棄却して「平均は70点から変わったと言える」になりました。

母分散が未知のとき、母平均の検定は、検定統計量$${T}$$を用いて$${t}$$分布の確率でいわゆる「$${t}$$検定」を行います。

$${\boldsymbol{t}}$$検定って？

母集団の分散である「母分散」は分からないのが通常です。
母集団のことが分からないから、標本をとって母集団に思いを巡らせるのですものね。
母分散の代わりに、標本データから算出可能な「標本不偏分散」を用いるのが$${t}$$検定です。
検定統計量$${T}$$の公式です。

検定統計量$${T=\cfrac{\bar{X}-\mu_0}{\sqrt{\hat{\sigma}^2/n}}=\cfrac{標本平均-帰無仮説の平均}{\sqrt{標本不偏分散/標本サイズ}}}$$

検定統計量$${Z}$$の式中の母平均を標本不偏分散に変えると、検定統計量$${T}$$に変身します。
検定統計量$${T}$$が自由度$${n-1}$$（標本サイズ－１）の$${t}$$分布に従う性質を利用して、母平均の検定を実施します。

$${\boldsymbol{t}}$$分布と統計量の計算値$${\boldsymbol{t}}$$値と$${\boldsymbol{p}}$$値

例題に沿って$${t}$$分布を確認しましょう。
標本サイズが$${64}$$なので、$${-1}$$した自由度$${63}$$の$${t}$$分布の確率密度関数をプロットしました。

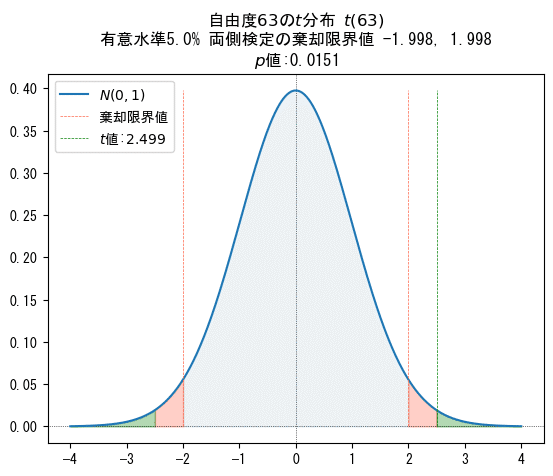
有意水準、両側検定の棄却限界値、検定統計量$${T}$$の計算値$${t}$$値、$${p}$$値を記載しています。
$${t}$$値$${2.499>}$$棄却限界値$${1.998}$$、または、有意水準$${0.05>p}$$値$${0.0151}$$より、帰無仮説は棄却されます。

計算、関数の使用

計算にはEXCELの関数を用いています。
$${t}$$分布特有の計算に関して、具体的な計算式を列挙いたします。

■標本不偏分散
　=VAR.S(C5:C1002)
■検定統計量T
　=(G11-G5)/SQRT(G12/G10)
■Tの上側確率
　=T.DIST.RT(G13,G10-1)
■p値
　=IF(G7="両側検定",2*MIN(G14,1-G14),IF(G7="片側検定(下側)",1-G14, IF(G7="片側検定(上側)",G14,0)))

特徴的な関数を紹介いたします。

【VAR.S関数】
標本データから標本不偏分散を算出する関数です。
引数は、VAR.S( 標本データの範囲 ) です。
検定統計量$${T}$$の計算に利用しています。

【T.DIST.RT関数】
$${t}$$分布の上側確率を算出する関数です。
引数は、T.DIST.RT( 検定統計量T, 標本サイズ-1 )です。
検定統計量$${T}$$の上側確率を用いて$${p}$$値を計算しています。

■検定統計量$${T}$$
専用の関数が見当たらないため、検定統計量$${T}$$の公式どおりの計算式を実装しました。

データやパラメータを変えてオリジナルの検定をしよう！

帰無仮説「平均は78.5点から変わっていない」（$${H_0: \mu=78.5}$$）
対立仮説「平均は78.5点より小さくなっている」（$${H_1: \mu<78.5}$$）

検定の結果、帰無仮説は棄却され、平均は78.5点より小さくなっていると言えます。
$${z}$$検定と同じ結果になりました。

まとめ

母平均の検定を２種類見ました。
１つは母分散が分かっているときに検定統計量$${Z}$$を用いる方法（$${z}$$検定）。
もう１つは母分散がわからないときに検定統計量$${T}$$を用いる方法（$${t}$$検定）。

確率分布と検定統計量の知識を活用して、EXCELの関数を活用して、サクッと統計的仮説検定を、ですね。

EXCELサンプルファイルのダウンロード
こちらのリンクからEXCELサンプルファイルをダウンロードできます。

Pythonで作成してみよう！

プログラムコードを読んで、データを流したりデータを変えてみたりして、データを追いかけることで、作表ロジックを把握する方法も効果的でしょう。
サンプルコードを揃えておけば、類似する作表作業を自動化して素早く結果を得ることができます。

今回は、①データが正規分布に従っているかの確認、②母平均の検定を実施します。

今回取り扱う母平均の検定は、標本データが正規分布に従っていること「データの正規性」が前提になっています。
Pythonで「データの正規性」を確認しましょう！

①インポート
scipy の stats をフル活用いたします！

from scipy import stats
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'MS Gothic'

②データの確認

データを読み込みます。

data = [66,53,71,47,36,89,73,85,72,54,57,76,93,54,60,76,67,75,86,66,51,70,
        39,75,51,63,86,67,56,63,75,83,90,95,80,56,97,84,99,75,75,68,68,68,
        64,89,94,56,81,98,97,79,85,98,82,61,79,100,94,92,85,90,95,91]

print(f'標本サイズ:{len(data)}, 標本平均:{np.mean(data):.2f}, '
      f'標本不偏分散:{np.var(data, ddof=1):.2f}')

出力イメージ

ヒストグラム

ヒストグラムの形状を確認しましょう。
seabornのhistplotを利用します。
正規分布の場合、綺麗な釣鐘型が描かれます。

sns.histplot(data, bins=10);

右肩上がりの形状です。
正規分布に従っていると言えるのでしょうか、心配になってきました。

正規Q-Qプロット

続いて、正規Q-Qプロットを描いて、データの正規性を確認しましょう。
scipy.stats の probplot を利用します。
引数は、probplot( データ, dist=分布（正規分布は'norm'）, plot=描画領域 )

正規分布に従っている場合、データ点は右肩上がりの直線の上に乗ります。

stats.probplot(data, dist='norm', plot=plt)
plt.show()

上端でデータ点が直線から大きく乖離していました！
試験の満点100点が上限となり、縦軸が100点を超えることができないことが、乖離・歪みの原因のような気がします。

このままでは、データの正規性が・・・。

では別の正規性の確認を行ってみます。

Shapiro-Wilk検定

シャピローウィルク検定です。
「標本分布は正規分布である」という帰無仮説を検定します。
有意水準を$${5\%}$$とし、$${p}$$値が$${0.05}$$を下回ったら、データの正規性が棄却されます。

scipy.stats の shapiro を利用します。
引数は、データそのものだけでＯＫです。

# Shapiro-Wilk検定　帰無仮説「標本の分布は正規分布である」
stats.shapiro(data)

出力イメージ

$${p}$$値は約$${0.08}$$です（pvalueの値です）。
有意水準$${5\%}$$で帰無仮説は棄却されません（ギリギリ・・・）。

つまり、一応「データの正規性は否定されない」結果が出ました。

すれすれかもですが、データが正規分布に従っていることを前提にして、母平均の検定を進めていきましょう！

さらっと流しましたが、データの正規性を確かめるコードがとても短いことにお気づきでしょうか？
Pythonでサクッとデータのチェックができるので、ぜひ、どんどんチェックしましょう！

③母平均の検定（母分散既知）：統計検定量$${Z}$$の利用

Pythonのライブラリに適切なものが無かったので、手組みしました。
まずは関数の定義です。
データ、有意水準、母分散、帰無仮説の平均、対立仮説の不等号等の扱い、を入力パラメータにして、z検定の結果を表示します。

def z_test_1sample_mean(data, alpha, sigma2_pop, mu0, H1='two-sided'):

    # 初期値設定
    test = {'two-sided': '両側検定', 'greater': '片側検定(>)', 'less': '片側検定(<)'}

    # 標本サイズ、標本平均、標本不偏分散の計算
    sample_size = len(data)
    X_bar = np.mean(data)
    var_ub = np.var(data, ddof=1)
    
    # z値の計算
    z = (X_bar - mu0) / np.sqrt(sigma2_pop / sample_size)
    
    # p値の計算
    if H1=='two-sided': # 両側検定
        p_value = 2 * (stats.norm.sf(x=np.abs(z), loc=0, scale=1))
    elif H1=='greater':  # 片側検定、対立仮説:μ>μ0の場合
        p_value = stats.norm.sf(x=z, loc=0, scale=1)
    elif H1=='less': # 片側検定、対立仮説:μ<μ0の場合
        p_value = stats.norm.cdf(x=z, loc=0, scale=1)
    
    # 帰無仮説の棄却／受容の判定
    if alpha > p_value:
        result = '棄却'
    else:
        result = '受容'
    
    # 結果表示
    print(f'*** 母平均の検定（母分散既知）の結果 ***\n'
          f'有意水準 {alpha:.1%} の{test[H1]}で 帰無仮説を {result}\n'
          f'検定統計量Z:{z:.3f}, p値:{p_value:.4f}\n'
          f'母平均（帰無仮説）:{mu0}, 母分散（既知）:{sigma2}, '
          f'標本平均:{X_bar:.2f}, 標本不偏分散:{var_ub:.2f}')

では、母分散既知の場合の母平均の検定を実行しましょう。
パラメータH1は、両側検定「two-sided」、片側検定（上側）「greater」、片側検定（下側）「less」のいずれかを設定します。

パラメータの設定値をさまざまに変えて、さまざまな検定を楽しんでくださいね。
この例では、例題の内容で検定をしています。

### 母平均の検定（母分散既知）：検定統計量Z

# 設定　母分散：sigma2、有意水準：alpha、帰無仮説の平均μ0：mu0、
# 対立仮説：H1→ two-sided:μ≠μ0、greater:μ>μ0、less:μ<μ0
sigma2, alpha, mu0, H1 = 16**2, 0.05, 70, 'two-sided'

# 母平均の検定（母分散既知）の実行、結果表示
z_test_1sample_mean(data, alpha, sigma2, mu0, H1)

想定どおり（？）、帰無仮説は棄却されました。
検定統計量$${Z}$$の計算値$${z}$$値と$${p}$$値を併記しています。

④母平均の検定（母分散未知）：検定統計量$${T}$$の利用

続いて、母分散未知の場合の母平均の検定に進みます。
scipy.stats の ttest_1samp で１標本の母平均の$${t}$$検定を実行できます。

早速、得点データを帰無仮説の平均70、両側検定で$${t}$$検定してみましょう。
引数 popmean に帰無仮説の平均（母集団の平均）、alternative に両側検定「two-sided」を設定します。

# ttest_1sampのお試し実行
stats.ttest_1samp(data, popmean=70, alternative='two-sided')

$${t}$$値（statistic）は2.499、$${p}$$値（pvalue）は0.015。
サクッと２つの値を出力できました。

検定結果で帰無仮説の棄却／受容を出力するコードにしてみます。
手組みと ttest_1samp の２パターンを作ります。

手組み
まずは関数定義から。

def t_test_1sample_mean(data, alpha, mu0, H1='two-sided'):
    
    # 初期値設定
    test = {'two-sided': '両側検定', 'greater': '片側検定(>)', 'less': '片側検定(<)'}

    # 標本サイズ、自由度、標本平均、標本不偏分散の計算
    sample_size = len(data)
    df = sample_size - 1
    X_bar = np.mean(data)
    var_ub = np.var(data, ddof=1)
    
    # t値の計算
    t_value = (X_bar - mu0) / np.sqrt(var_ub / sample_size)
    
    # p値の計算
    if H1=='two-sided': # 両側検定
        p_value = 2 * (stats.t.sf(x=np.abs(t_value), df=df))
    elif H1=='greater':  # 片側検定、対立仮説:μ>μ0の場合
        p_value = stats.t.sf(x=t_value, df=df)
    elif H1=='less': # 片側検定、対立仮説:μ<μ0の場合
        p_value = stats.t.cdf(x=t_value, df=df)
    
    # 帰無仮説の棄却／受容の判定
    if alpha > p_value:
        result = '棄却'
    else:
        result = '受容'
    
    # 結果表示
    print(f'*** 母平均の検定（母分散未知、t検定）の結果 ***\n'
          f'有意水準 {alpha:.1%} の{test[H1]}で 帰無仮説を {result}\n'
          f'検定統計量T:{t_value:.3f}, p値:{p_value:.4f}\n'
          f'母平均（帰無仮説）:{mu0}, 標本平均:{X_bar:.2f}, 標本不偏分散:{var_ub:.2f}')

続いて、検定の実行です。
パラメータの設定値をさまざまに変えて、さまざまな検定を楽しんでくださいね。
この例では、例題の内容で検定をしています。

### 母平均の検定（母分散未知）：検定統計量T

# 設定　有意水準：alpha、帰無仮説の平均μ0：mu0、
# 対立仮説：H1→ two-sided:μ≠μ0、greater:μ>μ0、less:μ<μ0
alpha, mu0, H1 = 0.05, 70, 'two-sided'

# 母平均の検定（母分散未知）の実行、結果表示
t_test_1sample_mean(data, alpha, mu0, H1)

帰無仮説は棄却されました。

ttest_1samp利用

「# t値、p値の取得」の部分に scipy.statsのttest_1samp を利用しました。
コード一行で$t$値と$p$値を取得できます！

# 設定　有意水準：alpha、帰無仮説の平均μ0：mu0、
# 対立仮説：H1→ two-sided:μ≠μ0、greater:μ>μ0、less:μ<μ0
alpha, mu0, H1 = 0.05, 70, 'two-sided'

# 初期値設定
test = {'two-sided': '両側検定', 'greater': '片側検定(>)', 'less': '片側検定(<)'}

# t値、p値の取得　scipy.statsのttest_1samp利用
t_value, p_value = stats.ttest_1samp(data, popmean=mu0, alternative=H1)

# 標本平均、標本不偏分散の計算
X_bar = np.mean(data)
var_ub = np.var(data, ddof=1)

# 帰無仮説の棄却／受容の判定
if alpha > p_value:
    result = '棄却'
else:
    result = '受容'

# 結果表示
print(f'*** 母平均の検定（母分散未知、t検定）の結果 ***\n'
      f'有意水準 {alpha:.1%} の{test[H1]}で 帰無仮説を {result}\n'
      f'検定統計量T:{t_value:.3f}, p値:{p_value:.4f}\n'
      f'母平均（帰無仮説）:{mu0}, 標本平均:{X_bar:.2f}, 標本不偏分散:{var_ub:.2f}')

ttest_1samp 利用の方も関数化すれば、検定の実行部分をシンプルにできます。

まとめ

小さなデータサイズでしたが、実際にデータを使って統計的仮説検定を実践しました。
統計的仮説検定は、データ件数の多さ、確率分布から確率を計算する難しさなどの要因から、コンピュータの活用が重要なテーマになります。

コンピュータが得意な方は、EXCELやPythonで、オリジナルの計算を実施する方法があるでしょう。
定型的なワークをサクッとこなす別の方法として、統計処理に特化した「統計解析ツール」を活用する方法があるでしょう。
本格的な統計的仮説検定を実施する際、定評のある「統計解析ツール」を用いて確実な統計計算を実施することで、数値の信頼性を高めてくれることでしょう。

統計解析ツールの例

下の図は、以前の記事で活用した「HAD」（無料の統計解析ツール）を用いて、１標本の母平均の$${t}$$検定を実施した結果を示しています。

サクッと統計の数字を計算してくれました。
統計的な計算方法を熟知していなくても統計数値を計算できる点で、便利なツールだと思います。
お好みの統計解析ツールが見つかるといいですね🌸

HADの情報は次のリンクでご覧いただけます。

Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。

おわりに

長文にもかかわらずお付き合いいただきまして、ありがとうございます。
仮説の成立性を検定統計量の計算値や$${p}$$値を用いて判断する流れはいかがだったでしょうか？

$${p}$$値に関しては、「$${p}$$値ハッキング」問題を巡って、誤ったデータ分析を危惧する声があるそうです。
参考記事は例えばこちら。

世の中、いろいろあるのですね・・・。
ツールは適切に使いこなしたいです。

最後までお読みいただきまして、ありがとうございました。

のんびり統計シリーズの記事

次の記事

前の記事

8-1 母平均の検定の考え方 ～ 統計的仮説検定の流れに身をまかせ～♪

今回の統計トピック

問題を解く

知る

おしながき

統計的仮説検定

例題で統計的仮説検定を体感する

実践する

母平均の検定を実行してみよう！

電卓・手作業で作成してみよう！

EXCELで作成してみよう！

Pythonで作成してみよう！

おわりに

のんびり統計シリーズの記事

いいなと思ったら応援しよう！

8-1 母平均の検定の考え方～統計的仮説検定の流れに身をまかせ～♪