見出し画像
Photo by mioarty

シリーズPython④ あたらしいベイズ統計の教科書を PyMC Ver.5で

ネイピア DS

はじめに

あたらしいベイズ統計の教科書の紹介

この記事は書籍「Pythonで動かして学ぶ! あたらしいベイズ統計の教科書」（翔泳社、以下「教科書」と呼びます）を PyMC Ver.5 で実践したときの留意点を取り扱います。

この教科書は、ベイズ統計の基礎理論と、MCMCを用いた事後分布・事後予測の推定を、初学者にわかりやすく解説する素晴らしい書籍です。
豊富なPythonコードを動かしながら、MCMCのコード、要約統計量、各種プロットの扱い方を学べます。

■ 注意点はPyMC3で書かれていること

注意が必要なのは、MCMCのツールに 「PyMC3」 を利用している点です。
PyMC3 は人気の高いMCMCパッケージですが、既に開発終了しています。
現在の PyMC シリーズの最新バージョンは Ver.5 です。
さらに注意が必要なのは、PyMC3 と PyMC Ver.5 の間で互換性が保たれていない部分があることです。

勉強で使ういろいろなマーク：「いらすとや」さんより

PyMC Ver.5 を用いて教科書に取り組むには、PyMC Ver.5 で動作するようにコードを変更する必要があります。
ネットには、日本語による PyMC Ver.5 の情報が乏しく、また、PyMC3 から PyMC Ver.5 への変換方法の情報も見つかりません。

PyMC 公式サイト（英語）を読み解きながらコードを探る必要があるのです。

「CAUTION」のイラスト文字：「いらすとや」さんより

■ PyMC Ver.5 で動かしたい

私はPyMC の学習をこの教科書から始めました。
せっかくなら新しいバージョンで取り組みたいと考えて、PyMC Ver.5 を使うことにしました。

結構、難儀しました。。。

この記事は、良書であるこの教科書で学びたいし、新しいPyMCパッケージで学びたい人向けに書きました。
特に、PyMC3 と PyMC Ver.5 の間でコードやデータ参照の仕方に変更があった部分に焦点をあてて、代替コードを掲載いたします。

入門して間もない私たちにとって、英語の公式サイトから情報を得て、コードの書き換えを行うことは、学習の立ち上がりに対して大きな障害になると思います。
できるだけこの障害を取り払って、本来的な学習に集中できるようになれたなら幸いです。

壁を乗り越える人のイラスト（男性）：「いらすとや」さんより

まえがき

この記事は、出典に記載の書籍に掲載された文章及びコードを引用し、適宜、掲載文章とコードを改変して書いています。
PyMC3 から PyMC Ver.5 への書き換えは「見つけることができた範囲内の処理内容」であり、処理の正確性は担保しておりません。
誤りや改善点がありましたら、ぜひ教えてください。

【出典】
「Pythonで動かして学ぶ! あたらしいベイズ統計の教科書」（初版第１刷、かくあき著、翔泳社）

お品書き

章単位に区切って、教科書のコードに付された「リスト番号」の単位で、代替コードと出力イメージを記載いたします。
なお、以下に該当するコードは、この記事では取り上げてていません。
・教科書のコードが動く場合
・記事で取り上げた代替コードを応用して動かせる場合

では、ベイズ統計と PyMC の旅へ進みましょう🚀

その前に、PyMCの公式サイトのご案内です。

第６章 6.2 PyMC3入門

章のタイトルは教科書の掲載のママです。

6.11 インポート
PyMC Ver.5 をインポートします。

# リスト6.11 PyMC5のインポート
import pymc as pm

バージョン確認
利用バージョンは 5.5.0 です。
これは、Anaconda環境の最新版です。
pip をお使いの方は PyMC の最新バージョン 5.6.0～ を利用できます。

# PyMCのバージョン確認
pm.__version__


>> 出力イメージ
>> '5.5.0'

6.14 正規分布を表すオブジェクト
PyMC Ver.5 の dist オブジェクトが大幅に変わったようです。
教科書通りの出力ができる代替策を見つけられませんでした。
なお、リスト 6.17 および 6.18 の方法で代替できると思われます。

# PyMC3どおりにできないコード
# PyMC5では、Normal.distで「分布classに対応するテンソル変数を作成する」

# リスト6.14 正規分布を表すオブジェクト
mu, sigma = 4, 1
dist = pm.Normal.dist(mu=mu, sigma=sigma)
dist


>> 出力イメージ
>> normal_rv{0, (0, 0), floatX, False}.out

6.15 正規分布の乱数の生成
確率分布から乱数を生成する関数が変更されています。

# リスト6.15 正規分布の乱数の生成
pm.draw(dist, 5, random_seed=1)  # 乱数の生成方法の変更

6.17 定義したモデルの数式表現
パラメータ設定値を出力するように変更されています。

# ★リスト6.17 定義したモデルの数式表現
model   # パラメータ値を出力
出力イメージ

6.18 モデルに定義されている確率変数
パラメータ設定値を出力するように変更されています。

# リスト6.18 モデルに定義されている確率変数
model.basic_RVs   # パラメータ値を出力


>> 出力イメージ
>> [X ~ Normal(4, 1)]

6.20 生成された乱数の確認
トレースオブジェクトのアクセス方法が大幅に変わっています。
教科書どおりに出力するには、arviz を利用して、トレースオブジェクトから extract データを作成するのが近道な感じです。

# リスト6.20 生成された乱数の確認

# extractデータの作成
import arviz as az
trace_ext = az.extract(trace)

# extractデータを利用　dataで配列を取り出す 
trace_ext['X'].data


>> 出力イメージ
>> array([3.57041046, 4.36657929, 3.73693532, ..., 5.4632591 , 4.55692973,
>>        4.49208405])

（参考）arvizのインストール

# pipの場合
pip install arviz

# condaの場合
conda install -c conda-forge arviz


緊急企画！

トレースオブジェクト「trace」と extract したデータ「trace_ext」の違いを確認してみましょう。

テミスのイラスト：「いらすとや」さんより

最初にトレースオブジェクト「trace」の中身を掘り下げて覗いていきます。

trace
出力イメージ

arviz の InferenceData の形式であり、「posterior」「sample_stats」の２つのグループがあることが分かりました。

「posterior」グループを掘り下げて見ましょう。

trace.posterior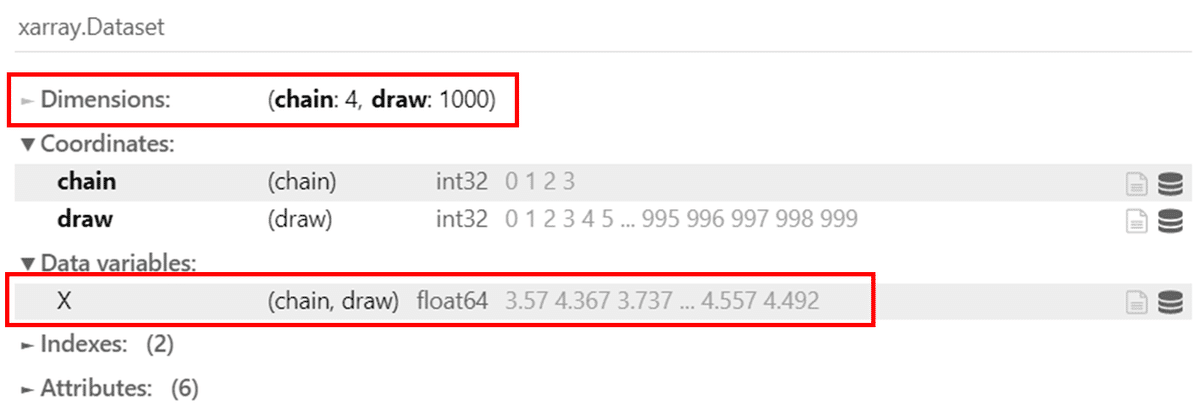
出力イメージ

データの形式が、xarray.Dataset に変わりました。
次元（Dimensions）は、chain : 4、draw : 1000 です。
4 チェーン、1000 ドローなので、データは合計 4000 個あります。
変数（Data variables）に X を発見しました。
X の形状が ( chain, draw ) であり、つまり、データは ( 4, 1000 ) の形状で格納されていることが分かります。

変数 X を掘り下げます。

trace.posterior['X']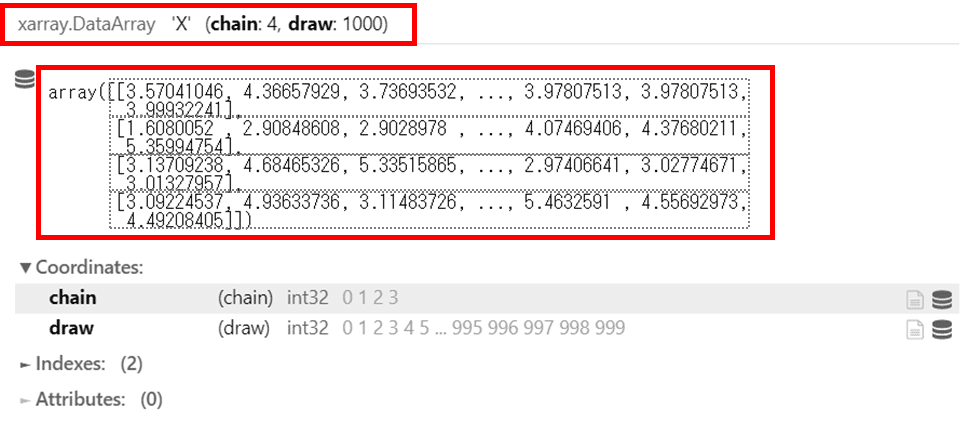
出力イメージ

データの形式が xarray.DataArray に変わりました。
”X" の形状は　(chain : 4,  draw : 1000)　と表記されています。
array の箇所に、X のデータが４つに区切られて表示されています。

data メソッドを用いて、X データを取り出してみましょう。
まず、trace.posterior['X'] の状態で取り出してみます。

print(trace.posterior['X'].data.shape)
trace.posterior['X'].data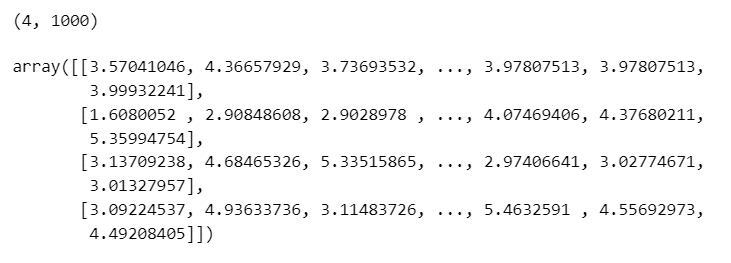
出力イメージ

形状は (4, 1000) 。配列は 4 行 1000 列 になっています。

１次元にしてみましょう。
ここでは NumPy の flatten() を使いました。

print(trace.posterior['X'].data.flatten().shape)
trace.posterior['X'].data.flatten()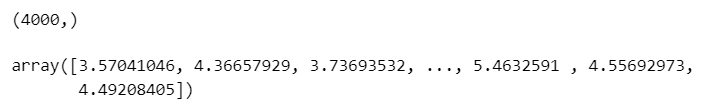
出力イメージ

リスト 6.20 の出力をトレースオブジェクト trace から行う場合には、このコードのように、データを掘り下げて取得することとなります。

モグラの工事作業員のイラスト（穴）：「いらすとや」さんより

続いて、 extract したデータ「trace_ext」を掘り下げます。

trace_ext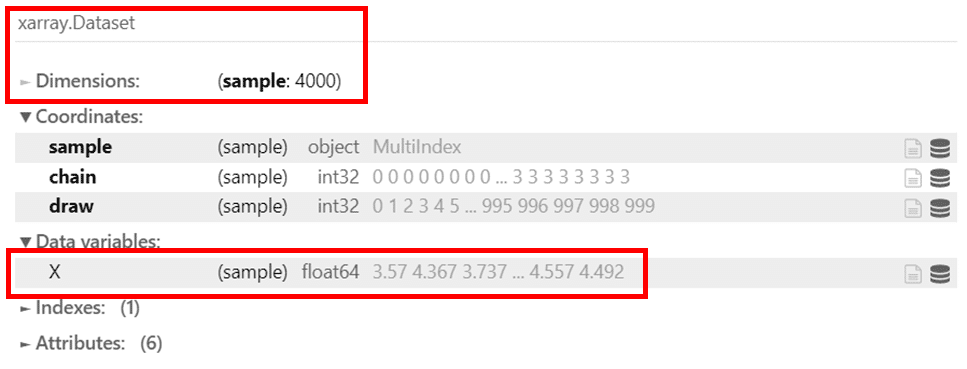
出力イメージ

データの形式は、xarray.Dataset です。
トレースオブジェクトを trace.posterior としたときと同じ形式になりました。
実は、az.extract( trace ) を実行することで、トレースオブジェクトの 「posterior」グループを取り出していたのです。

そして、次元（Dimensions）は、sample : 4000 です。
chain と draw の次元が無くなって１次元に変わりました。
変数 X の箇所にも 次元が ( sample ) であることが表記されています。

変数 X を掘り下げます。

trace_ext['X']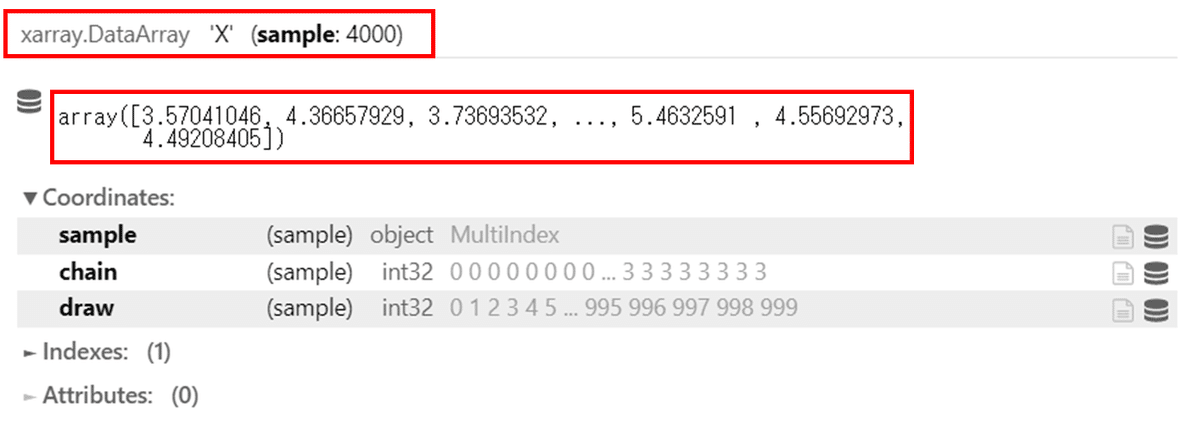
出力イメージ

データの形式が xarray.DataArray に変わりました。
”X" の形状は　(sample : 4000)　と表記されています。
array の箇所に、X のデータが１次元で表示されています。

data メソッドを用いて、X データを取り出してみましょう。

print(trace_ext['X'].data.shape)
trace_ext['X'].data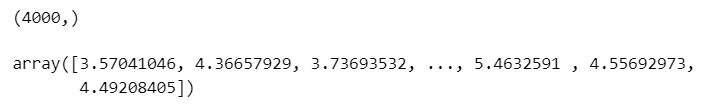
出力イメージ

リスト6.20 の出力を得ることができました。

トレースオブジェクトを直接操作する場合、az.extract で操作対象のデータを「取り出して」おくのが良さそうです。

次のコードに移ります。

木の看板のウェブ用ナビゲーションボタン（日本語）：「いらすとや」さんより

6.21 乱数の生成回数の確認
extract データを利用するように変更しました。

# リスト6.21 乱数の生成回数の確認
trace_ext['X'].shape  # extractデータを利用


>> 出力イメージ
>> (4000,)

6.22 サンプリング結果をデータフレームで扱う方法
extract データを利用するように変更しました。
テキストどおりに変数 X だけ出力するよう、[['X']].reset_index(drop=True) を付けました。

# リスト6.22 サンプリング結果をデータフレームで扱う方法
trace_ext.to_dataframe()[['X']].reset_index(drop=True)  # extractデータを利用
出力イメージ

6.23 ヒストグラムとカーネル密度
extract データを利用するように変更しました。
リスト 6.27 も同じ変更をします。

# リスト6.23 ヒストグラムとカーネル密度推定
import matplotlib.pyplot as plt
import seaborn as sns

fig, ax = plt.subplots(constrained_layout=True)
sns.histplot(trace_ext['X'],                       # extractデータを利用
             stat='density', kde=True, ax=ax)
plt.show()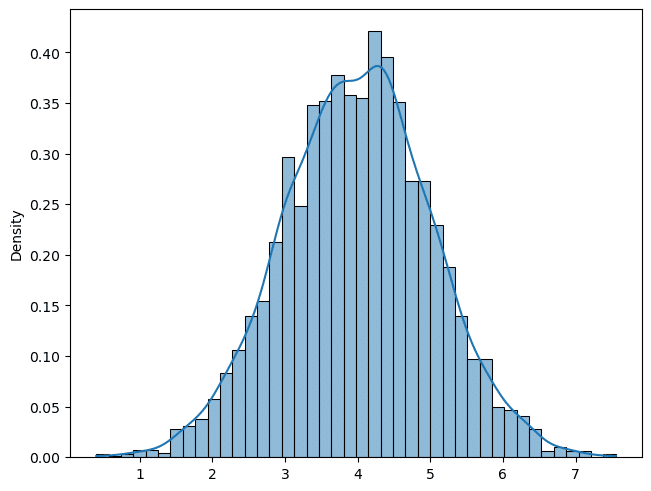
出力イメージ

6.36 事後期待値と事後中央値
arviz で トレースオブジェクトから extract データを作成して、extract データを利用するように変更しました。
また、値を取り出すのに item() を付けました。

# リスト6.36 事後期待値と事後中央値

# exctactデータの作成
trace_ext = az.extract(trace)

mu = trace_ext['lambda'].mean().item()    # extractデータ利用、item()を付ける
sigma = trace_ext['lambda'].std().item()  # extractデータ利用、item()を付ける

print(f'EAP = {mu}')
print(f'MED = {sigma}')


>> 出力イメージ
>> EAP = 2.8576212743888108
>> MED = 1.193687310001302

小まとめ

トレースオブジェクト（trace）に直接アクセスする場合、az.extract でデータを取り出しておくと、コードと配列がシンプルになり、アクセスしやすくなりました。
一方で、pm.summary() や pm.plot_trace() などの関数でトレースオブジェクトを扱う際は、トレースオブジェクト（trace）を引数に指定します。
extract データを指定するとうまく動きません。

勉強で使ういろいろなマーク：「いらすとや」さんより

第７章 7.2 MCMCの診断情報

第７章のコードのうち、トレースオブジェクトのアクセスに関しては、先の第６章の代替コードを参考にしてください。

ここでは、トレースオブジェクトの保存と読み込みに関する代替策を記載いたします。

実は、トレースオブジェクトを保存できる PyMC Ver.5 の関数やメソッドを見つけられませんでした。

代替策の１つは pickle を利用することです。

7.9 データの保存

# リスト7.9 データの保存の代替案  ★pickleの利用
import pickle
file = r'./data/sample.pkl'
with open(file, 'wb') as f:
    pickle.dump(trace, f)

7.10 データの読み込み

# リスト7.10 データの読み込みの代替案  ★pickleの利用
with model:
    trace_l = pickle.load(open(file, 'rb'))

別の代替策は、arviz による netcdf 型データへのアクセスを利用するものです

7.9 データの保存

# リスト7.9 データの保存の代替案  ★to_netcdfの利用
trace.to_netcdf(r'./data/trace.nc')

7.10 データの読み込み

# リスト7.10 データの読み込みの代替案  ★from_netcdfの利用
trace = az.from_netcdf(r'./data/trace.nc')
セーブポイントのイラスト：「いらすとや」さんより

第８章 8.1 線形回帰

第８章のコードのうち、トレースオブジェクトのアクセスに関連する代表的な代替コードを検討します。

8.27 $${\boldsymbol{\beta_0}}$$の推定値
extract データを作成します。

# リスト8.27 β0の推定値

# exctactデータの作成
trace_c_ext = az.extract(trace_c)

# exctactデータ利用
beta0 = trace_c_ext['beta0'] - trace_c_ext['beta1'] * data['wt'].mean()
beta0.mean().item()

8.28 生成された乱数の配列の形状
extract データ trace_c_ext の形状（32, 4000）は、教科書のトレースオブジェクト trace_c の形状（4000, 32）と次元が逆転しています。
後続処理で次元を指定する場合に注意が必要です。

# リスト8.28 生成された乱数の配列の形状　★教科書のtrace_cは(4000, 32)
trace_c_ext['mu'].shape

>> 出力イメージ
>> (32, 4000)

8.29 回帰直線とその不確かさを図示
extract データ trace_c_ext の形状が教科書のトレースオブジェクト trace_c の形状と逆転している影響をふまえて、コード変更します。

  • trace_c_ext['mu'].mean(axis=1)　：axisを0から1へ変更

  • trace_c_ext['mu'].shape[1], 20　： shape[1]で長さを取得

  • trace_c_ext['mu'][:, i]　： i を動かす次元が異なる

# リスト8.29 回帰直線とその不確かさを図示

fig, ax = plt.subplots(constrained_layout=True)

ax.scatter(data['wt'], data.mpg, label='data')
ax.plot(data['wt'], trace_c_ext['mu'].mean(axis=1),  # extractデータ利用
        'k', label='mean')

for i in range(0, trace_c_ext['mu'].shape[1], 20):   # extractデータ利用
    ax.plot(data['wt'], trace_c_ext['mu'][:, i],     # extractデータ利用
            'gray', alpha=0.05)

ax.set_xlabel('wt')
ax.set_ylabel('mpg')
ax.legend()
plt.show()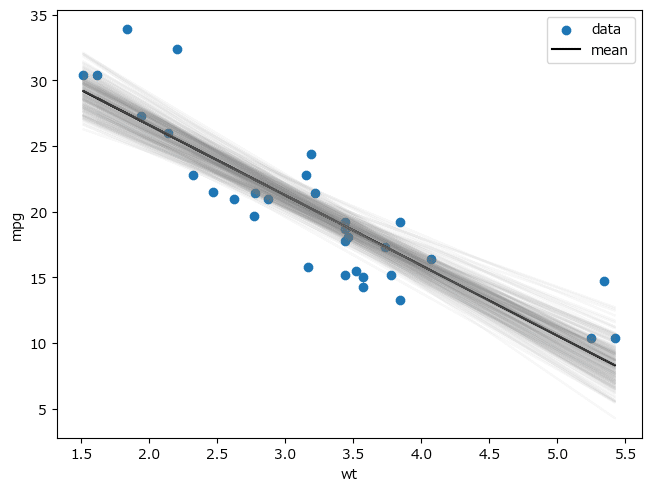
出力イメージ

8.32 回帰直線のHDIを表示
「extract データ」と「事後予測の配列データ」の使い分けの例です。

  • extract データを利用できる matplotlib には「trace_c_ext['mu'].mean(axis=1)」のように extract データを指定できます。
    教科書の形状と逆転しているので、平均をとる次元を axis=1 に変更しています。

  • plot_hdi 関数には事後予測 sample_posterior_predictive 関数で取得した配列データ pp を渡す必要があります。
    「pp.posterior_predictive['mpg']」のように「posterior_predictive」を付けます。

# リスト8.32 回帰直線のHDIを表示

fig, ax = plt.subplots(constrained_layout=True)

ax.scatter(data['wt'], data.mpg, label='data')
ax.plot(data['wt'], trace_c_ext['mu'].mean(axis=1),   # extractデータ利用
        'k', label='mean')

# plot_hdiは(chain, draw, dim)のshapeを要求するのでpp.posterior_predictiveを利用
pm.plot_hdi(data['wt'], pp.posterior_predictive['mpg'], ax=ax,
            fill_kwargs={'color': 'gray', 'alpha': 0.3, 'label': r'$94\%$ HDI'})

pm.plot_hdi(data['wt'], pp.posterior_predictive['mpg'], hdi_prob=0.5, ax=ax,
            fill_kwargs={'color': 'gray', 'alpha': 0.8, 'label': r'$50\%$ HDI'})

ax.set_xlabel('wt')
ax.set_ylabel('mpg')
ax.legend()
plt.show()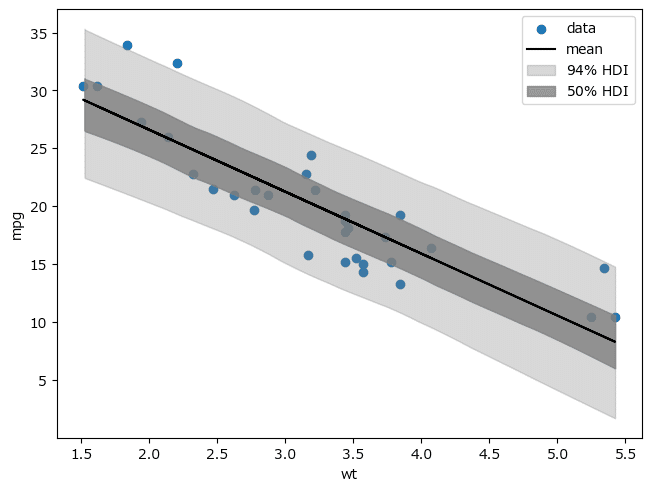
出力イメージ

小まとめ

az.extract でトレースオブジェクトから取り出した extract データの形状が、PyMC3（教科書）と逆転しています。
次元を指定してデータアクセスするケースでは、extract データの形状に沿うようにコードを変更します。

事後予測 sample_posterior_predictive 関数で取得した事後予測の配列 pp を利用する pm.plot_hdi 関数などでは、データの型に含まれる「posterior_predictive」を指定します。
例えば、pp.posterior_predictive['mu'] のような表記です。

第９章 9.1.2 GLMモジュール

第９章のコードのうち、トレースオブジェクトのアクセスに関しては、先の第６章・第８章の代替コードを参考にしてください。

ここでは、pm.GLM.from_formula 関数の代替策を記載いたします。

F1カー・フォーミュラーカーのイラスト：「いらすとや」さんより

実は、PyMC Ver.5 のGLMモジュールに from_formula 関数を見つけられませんでした。
ネットで代替策を探したところ、「Bambi」に行き着きました。
「ベイズモデル構築インターフェイス」です。

子鹿・バンビのイラスト：「いらすとや」さんより

Bambiの公式サイトです。

インストール

# pipの場合
pip install bambi

# condaの場合
conda install -c conda-forge bambi

9.3 pm.GLM.from_formula関数の例
bambi をインポートして、モデル定義とサンプリングを実行します。
モデル定義は from_formula 関数と似た構文のようです。
サンプリング実行は、model に対して fit メソッドを用いて行うようです。

# リスト9.3 pm.GLM.from_formula関数の例
import pymc as pm
import bambi as bmb
model = bmb.Model('y ~ x', data)   # モデルの定義
trace = model.fit(random_seed=1)   # サンプリング
出力イメージ

モデルを表示します。
9.3 のモデルの定義で指定していない項目は、bambiが補完しているようです。

# 定義したモデルの表示
model
出力イメージ

モデルをグラフ図で表示します。
説明変数 x 、Intercept（切片）、目的変数 y には正規分布、y_sigma（目的変数 y の標準偏差）には半スチューデントのｔ分布が、bambiによって割り当てられているようです。

# モデルのグラフ図の描画
model.graph()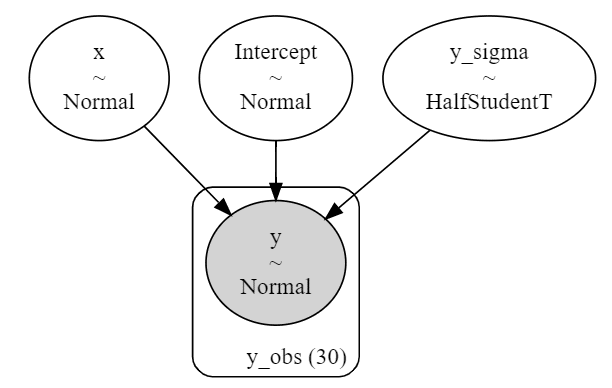
出力イメージ

9.4 family引数に指定できる確率分布の一覧
適切なコードを見つけられませんでした。

9.5 priors引数とfamily引数の指定方法の例
コード全体に渡って、bambi用に書き換えました。

# リスト9.5 priors引数とfamily引数の指定方法の例
priors = {
    'Intercept': bmb.Prior('Normal', mu=0, sigma=100),
    'x': bmb.Prior('Normal', mu=0, sigma=100)
}
model = bmb.Model('y ~ x', data, priors=priors, family='gaussian')
trace = model.fit()
出力イメージ

モデルを表示します。

# 定義したモデルの表示
model
出力イメージ

モデルをグラフ図で表示します。

# モデルのグラフの図描画
model.graph()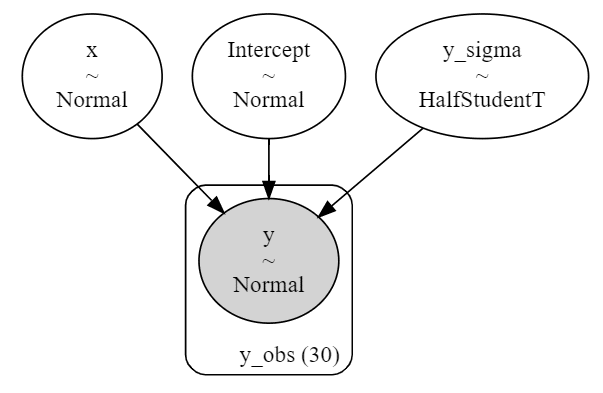
出力イメージ

9.6 トレースプロットを表示
bambiを通じて取得したトレースオブジェクトをトレースプロットに描画する際には、テキストのコードのとおり「PyMCを用いて」描画可能です。
また、arvizでも同様に描画可能です。

# リスト9.6 トレースプロットを表示
pm.plot_trace(trace)
plt.tight_layout();
 
# import arviz as az
# az.plot_trace(trace)
# plt.tight_layout()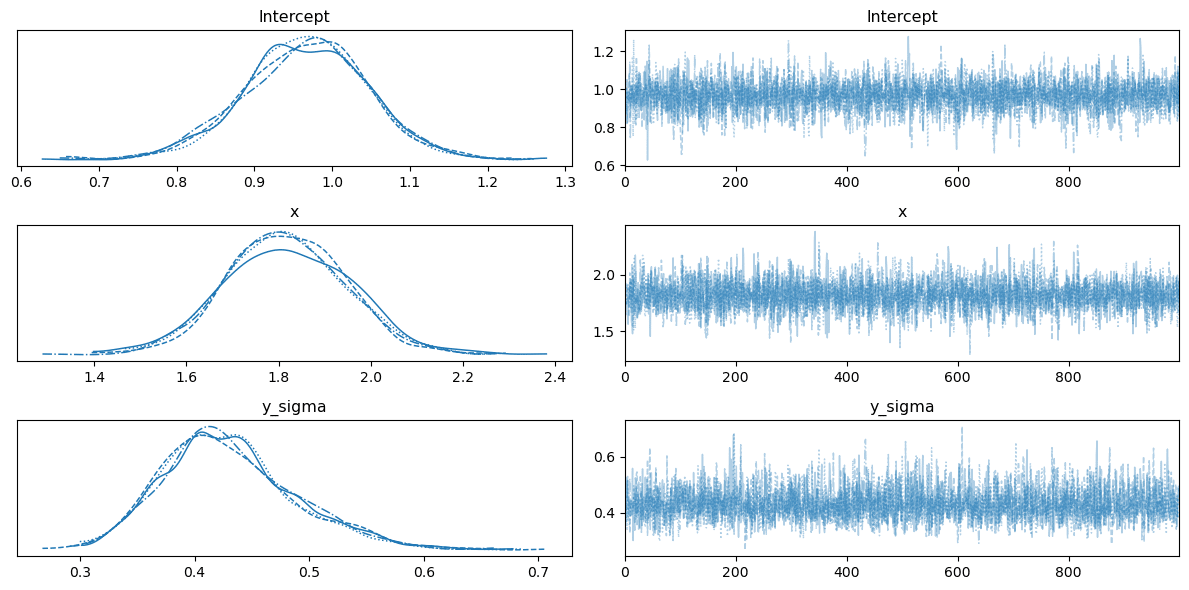
出力イメージ

結び

PyMC3 から PyMC Ver.5 へ進む道はかなり険しい感じがしました。
PyMC Ver.5 ベースの書籍が出版されることを願ってやみません。

今回の取組みで分かったことは、「トレースオブジェクトのデータ形式」と「formulaを用いたモデル構築」を調べることの難易度が高いことです。

教科書では PyMC3 の流儀でコードを書かれています。
一方で PyMC Ver.5 は流儀が変わっています。
PyMC Ver.5 の流儀に沿うことで、PyMC の関数やメソッドが「データ形式」をブラックボックス化してくれるでしょう。
また、Bambi の流儀に沿うことで、Bambi のチュートリアル「foumula の構文例」を活用できるようになり、頭を悩ますことが減るような気がします。

また直ぐ目の前には、Theano から PyTensor への変換という大きな壁が立ちはだかっています。
この壁もなんとかして乗り越えたいです。

最後に、データ形式とBambiの公式サイトのリンクを置いておきます。

１．トレースレースオブジェクトのデータ形式
① ArviZ の InferenceData

② xarray の Dataset

③ xarray の DataArray

２．formulaを用いたモデル構築
・Bambi

おわり

ブログの紹介

noteで３つのシリーズ記事を書いています。
ぜひ覗いていってくださいね！

１．のんびり統計
統計検定２級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定２級公式問題集CBT対応版に対応しています。

２．Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。

３．データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。

最後までお読みいただきまして、ありがとうございました。


いいなと思ったら応援しよう！