
8-4 母比率の検定の手順 ~ 細工されたコイントスを暴け!
今回の統計トピック
統計的仮説検定のトピック「1標本の母比率の$${z}$$検定」を深掘りします。
100回コイントスチャレンジを1000セット繰り返して表の出る割合を検定します!(もちろん手作業じゃなくて、EXCELやPythonで実装します)
公式問題集の準備
「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください!
「知る」「実践する」の章で、のんびり統計をお楽しみください!
問題を解く
📘公式問題集のカテゴリ
検定の分野
問4 母比率の検定の手順(コイントス)
試験実施年月
調査中
問題
公式問題集をご参照ください。
解き方
題意
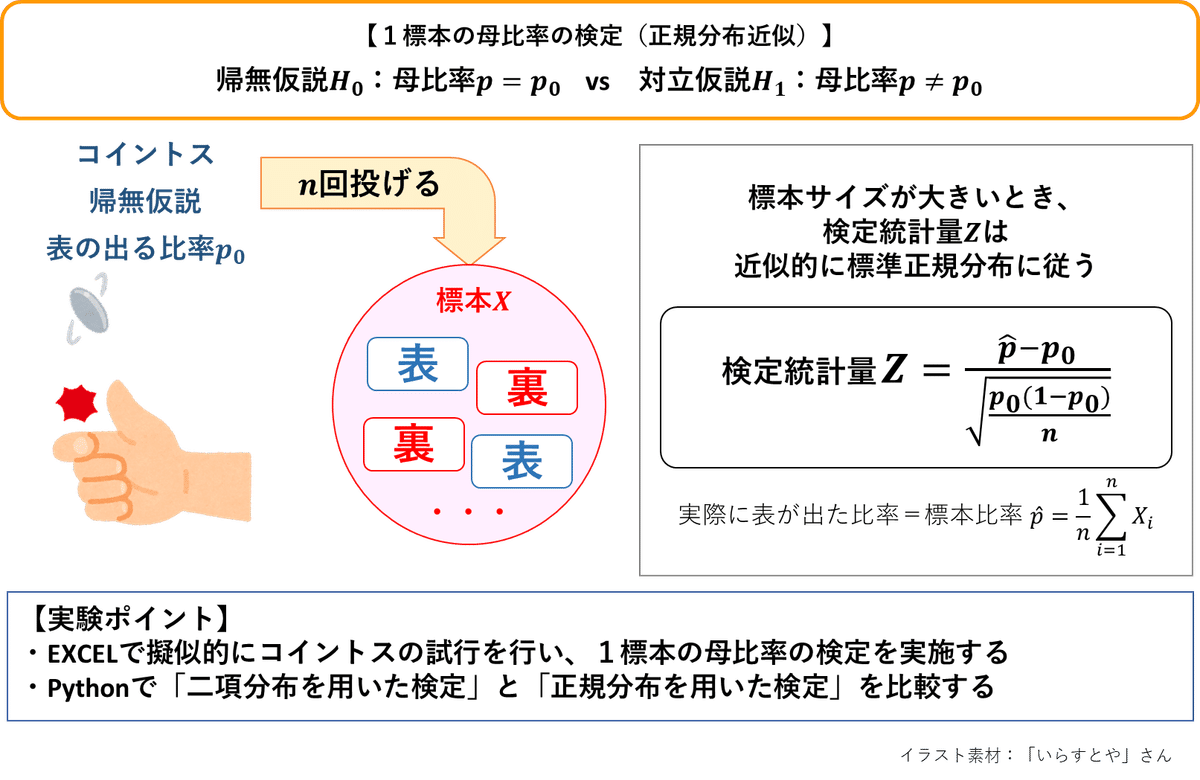
正規分布近似を利用した1標本の母比率の検定について、検定の方法、棄却域、帰無仮説を棄却する/しないの判定を行います。
■条件
母比率$${p}$$、標本比率$${\hat{p}}$$、標本サイズ$${n}$$のとき、
・帰無仮説$${H_0:p=p_0}$$(母比率は$${p_0}$$と等しい)
・対立仮説$${H_0:p\neq p_0}$$(母比率は$${p_0}$$と等しくない)
・検定統計量$${Z=\cfrac{\hat{p}-p_0}{\sqrt{p_0(1-p_0)/n}}}$$は$${n}$$が大きいとき、帰無仮説$${H_0}$$のもとで標準正規分布に近似的に従う
・有意水準は5%
両側検定・片側検定の識別
対立仮説は$${H_0:p\neq p_0}$$であり、「≠」なので両側検定です。
解答選択肢の(ア)は「両側」です。
両側検定と片側検定の違いをグラフで確認しましょう。
・対立仮説$${H_0:p \neq p_0}$$のときは両側検定
・対立仮説$${H_0:p > p_0}$$のときは片側検定(上側確率で判断)
・対立仮説$${H_0:p < p_0}$$のときは片側検定(下側確率で判断)

棄却域
出題条件より、検定統計量$${Z}$$は近似的に標準正規分布に従います。
両側検定の場合、検定統計量$${Z}$$の計算値である$${z}$$値が、有意水準 5% の半分である 2.5% の点$${z_{0.025}}$$よりも大きいとき、帰無仮説は棄却されます。
標準正規分布の上側確率表を見ましょう。
$${z_{0.025}}$$は 1.96 です。

棄却域は$${|z| > 1.96}$$です。
解答選択肢の(イ)は「$${|z| > 1.96}$$」です。
棄却域をグラフで確認しましょう。
両側検定(左)では、$${z}$$値が$${-1.96}$$より小さいときか、$${1.96}$$より大きいときに、棄却域(青色)に該当します。

帰無仮説を棄却する/しないの判定
有意水準5%の両側検定では、計算した$${z}$$値が$${|z| > 1.96}$$になるとき、棄却域の値を取ることになり、帰無仮説は棄却されます。
解答選択肢の(ウ)は「帰無」(仮説)です。
グラフで確認しましょう。
$${z}$$値が棄却限界値$${|1.96|}$$(赤い点線)よりも外側の場合、対応する棄却域(青色の面積)は滅多に起きないことの確率を示しています。
$${|z| > 1.96}$$のとき、「帰無仮説が正しいならば滅多に起きない(発生確率が小さい)ことが、『現実に』起きています。偶然に起きたのではなく帰無仮説が正しくないと考えるのが適切でしょう」と考えて、帰無仮説を棄却します。

解答
⑤ です。
難易度 やさしい
・知識:1標本の母比率の検定(正規分布近似)
・計算力:なし
・時間目安:1分
知る
おしながき
公式問題集の問題に接近してみましょう!
今回は、1標本の母比率の検定の流れを確認します。
1標本の母比率の検定
📕公式テキスト:4.3.4 母比率に関する検定(148ページ~)
母比率の検定は正規分布近似を利用する
統計検定2級で出題される1標本の母比率の検定は、次を理由にして、正規分布近似を用いているようです。
①母集団$${N}$$が大きい
成功回数$${x}$$は二項分布に近似するものとして取り扱います。
厳密には$${x}$$は超幾何分布に従います。
②標本サイズ$${\boldsymbol{n}}$$が大きい
標本比率$${\hat{p}=x/n}$$を標準化して得られる検定統計量$${z}$$は近似的に標準正規分布に従います。
二項分布に関する中心極限定理を利用します。
検定統計量$${z}$$
帰無仮説が正しいと仮定して、帰無仮説の母比率$${p=p_0}$$を用いて検定統計量$${z}$$を算出します。
■1標本の母比率の検定統計量$${z}$$の公式(正規分布近似)
検定統計量$${z=\cfrac{\hat{p}-p_0}{\sqrt{p_0(1-p_0)/n}} \ \sim N(0,1)}$$
($${\hat{p}}$$:標本比率、$${p_0}$$:帰無仮説の母比率、$${n}$$:標本サイズ)
棄却限界値
標準正規分布を用いるので、棄却限界値は「標準正規分布の上側確率表」から取得します。
取得する値を$${z_{prob}}$$のように、確率$${prob}$$を付けて表記します。
(例)
・有意水準5%の両側検定の場合は$${z_{\alpha/2}=\pm z_{0.025}}$$
・有意水準5%の片側検定の場合、
・上側(右側)検定:$${z_{\alpha}=z_{0.05}}$$
・下側(左側)検定:$${z_{\alpha}=-z_{0.05}}$$
標準正規分布の上側確率表を見ます。
$${z_{0.025}=1.96}$$(黄色)、$${z_{0.05}=1.645}$$(ピンク)です。
ぴったり当てはまる確率値がない場合は、ピンクのように前後の値より補間して取得します。

■主要な標準正規分布の上側確率パーセント点
・確率 1.0%: $${z_{0.01}=2.326}$$
・確率 2.5%: $${z_{0.025}=1.96}$$
・確率 5.0%: $${z_{0.05}=1.645}$$
・確率 10.0%: $${z_{0.1}=1.282}$$
棄却する/しないの判定
検定統計量$${z}$$の計算値$${z}$$値を棄却限界値$${z_{prob}}$$と比較して、帰無仮説を棄却できるかどうかを判定します。
$${z}$$値の絶対値が棄却限界値よりも大きいとき、帰無仮説を棄却します。
(例)
有意水準5%の両側検定の場合は$${|z| > z_{0.025}=1.96}$$のとき帰無仮説を棄却します。
有意水準5%の片側検定の場合、
・上側(右側)検定:$${z > z_{0.05}=1.645}$$のとき帰無仮説を棄却します。
・下側(左側)検定:$${z < -z_{0.05}=-1.645}$$のとき帰無仮説を棄却します。

実践する
コイントスの実験をしてみよう!
今回は、コイントスの実験をして母比率の検定をシミュレーションしましょう。
実験の概要を図示します。
一定の確率(真の母比率)に基づいてコンピュータで乱数を発生させて、コインの表・裏データをランダムに$${n}$$個作成します。
帰無仮説の母比率$${p_0}$$が正しいと仮定して検定を行い、帰無仮説を棄却する/しないを判定します。
電卓・手作業で作成してみよう!
EXCEL、Pythonの試行をご覧いただき、実際にコインをトスして、手作業で検定を実施するのもありかもです。
一番記憶に残る方法ですし、試験本番のトレーニングにもなります。
EXCELで作成してみよう!
データ数が多い場合、やはり手作業では非効率になります。
パソコンを利用して、手早く作表できるようになれば、実務活用がしやすくなるでしょう。
コイントス実験スタート!
EXCELで擬似的にコイントスを100回行って、表が出た回数の割合=標本比率$${\hat{p}}$$を得ます。

実験シートの紹介
「真の母比率」にコインの表が出る確率を設定します。

EXCELを少し動かすと、「真の母比率」の確率に従って、左側のデータエリアに「表(1)、裏(0)」のコイントスデータ100個を生成します。
くじ引きマシン「ガラポン」が自動で回っている感じ。

100個のコイントスデータから標本比率$${\hat{p}}$$を求めて、「計算値」エリアの$${z}$$値と$${p}$$値を計算します。
$${p}$$値が有意水準を下回るとき、帰無仮説を棄却します。
具体的なシナリオに当てはめる
表が出やすいと噂されているコイン(表の出る確率が$${0.55}$$)が手元にあります。
「真の母比率」に「$${0.55}$$」を設定します。「コインの表の出る確率は半々」では無いことを、統計的仮説検定で明らかにしましょう。
帰無仮説は覆したい比率「コインの表の出る確率は半々($${0.5}$$)である」です。
「帰無仮説の母比率」に「$${0.5}$$」を設定します。対立仮説は「コインの表が出る確率は$${0.5}$$より大きい」にしましょう。
「検定方法」に「片側検定(上側)」を設定します。
有意水準を$${5\%}$$にしましょう。
このコインを100回投げた結果が下の図です。
表の出た比率は$${0.66}$$でした(表の回数が66回)。

片側検定(上側)の結果、$${p}$$値$${=0.0007}$$となり、有意水準$${5\%}$$を下回るので、帰無仮説「コインの表の出る確率は半々($${0.5}$$)である」を棄却します。
ちなみに、表の出る確率(真の母比率)が$${0.55}$$のコインの場合、なかなか帰無仮説「コインの表の出る確率は半々($${0.5}$$)である」を棄却できる標本比率を得ることができません。
感覚的に、実験を何度も繰り返したときに、実験10回に1度くらい、棄却できる感じです。
コインの表をもう少し出やすくする
表の出る確率(真の母比率)を$${0.6}$$にすると、かなりの頻度で帰無仮説「コインの表の出る確率は半々($${0.5}$$)である」を棄却できます。

みなさんもご一緒に!
「真の母比率」(コインのイカサマの度合い)、「帰無仮説の比率」(覆したい仮説の比率)、有意水準、検定方法を変えてみて、コイントス実験を楽しんでくださいね。

EXCEL関数の紹介
■コインの表・裏をランダムに生成する方法
RAND関数で0以上1未満の乱数を取得できます。
取得した乱数が「真の母比率」未満のときに「表」(値は1)、これ以外のときに「裏」(値は0)となるように、IF関数で指定します。

■$${z}$$値の計算
STANDARDIZE関数を用いて、標本比率を標準化しています。
引数は、STANDARDIZE( 標準化したい値「標本比率」, 平均「帰無仮説の母比率」, 標準偏差 ) です。

■$${z}$$値の上側確率
NORM.S.DIST関数で標準正規分布の下側確率を算出して、1から下側確率を差し引いて、上側確率を算出します。
NORM.S.DIST関数の引数は、NORM.S.DIST( z値, TRUE「累積分布関数」) です。

EXCELサンプルファイルのダウンロード
こちらのリンクからEXCELサンプルファイルをダウンロードできます。
Pythonで作成してみよう!
プログラムコードを読んで、データを流したりデータを変えてみたりして、データを追いかけることで、作表ロジックを把握する方法も効果的でしょう。
サンプルコードを揃えておけば、類似する作表作業を自動化して素早く結果を得ることができます。
今回は、二項分布と正規分布を比較するシミュレーションを実施します。
標本サイズ$${n}$$が大きいとき、二項分布の正規分布近似を利用して、母比率の検定を行います。
本当に標本サイズ$${n}$$が大きいとき、本当に二項分布は正規分布に近似するのでしょうか?
実験しましょう!
実験の概要
コイントスの標本サイズ$${n}$$は、投げる回数のことです。
標本サイズ$${n}$$は、大きいだろうと囁かれる「100回」にしてみます。
100回のコイントスで標本比率$${\hat{p}}$$を求めます。
100回のコイントスを1セットの実験にして、1000セットの実験を繰り返します。
1000セットの実験の中には、コイントスのランダム性から、帰無仮説が棄却される場合と棄却されない場合が生じえます。
「二項分布の確率で検定をするケース」と「正規分布近似で検定をするケース」で、帰無仮説を棄却するセット数が一致するかどうかを、実験で確認します。

①インポート
# 数値計算・統計計算
import numpy as np
from scipy import stats
# 可視化
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Meiryo'②パラメータ設定
コインの表が出る確率を$${0.45}$$に設定します。
少し表が出にくいです。
帰無仮説の母比率は$${0.5}$$。表が出る確率が半々にならないことを検定します。
有意水準は$${5\%}$$。両側検定で行います。
なお、パラメータは変更可能です。
さまざまな値に変更して実験してみてくださいね。
# パラメータ設定
p = 0.45 # 真の母比率
p0 = 0.5 # 帰無仮説の母比率
n = 100 # コイントスの回数(試行回数)
num_trials = 1000 # 実験セット数
alpha = 0.05 # 有意水準
np.random.seed(5) # 乱数シード③コイントス
100回投げる実験を1000セット実施します。
numpy の random.rand で0以上1未満の乱数を生成して、真の母比率よりも小さいときに表、これ以外のときに裏にします。
sample_list には、1000セット✕100投 のデータが格納されています。
最後のコードで、1セット目の最初の10投のデータを表示します。
# n回のコイントスを実験セット数num_trials回行う
sample_list = []
for trial in range(num_trials):
# コイントス 乱数が真の母比率より小さい場合、表(True)にする
sample_list.append([np.random.rand() < p for _ in range(n)])
# 実験回数1回目のコイントスの最初の10投
print('実験1セット目のコイントスで最初の10投(表:True、裏:False)')
print(sample_list[0][:10])
表はTrue、裏はFalseの値で格納されています。

④二項分布で検定
いよいよ検定です。
■二項分布で考える
標本データ sample_list の「表の出る回数$${x}$$」を検定統計量にして検定します。
表の出る回数$${x}$$は、試行回数$${n=100}$$、成功確率=帰無仮説の母比率$${p_0=0.5}$$の二項分布$${Bin(100,0.5)}$$に従います。
■棄却限界値
「# 帰無仮説H0が正しいと仮定して、両側検定の棄却限界値の算出」で棄却限界値を算定しています。
二項分布$${Bin(100,0.5)}$$の上側確率・下側確率それぞれ$${0.025}$$になる点を lower と upper に格納します。
lower と upper が棄却限界値になります。
■検定
「# 棄却する/しないを判定」で「表の出る回数$${x}$$」が棄却域かどうかをチェックして、棄却する/棄却しないを判定します。
判定結果は test_result に格納します。
では、実行しましょう。
### 二項分布で検定
# 初期値設定
x_result = []
test_result = []
# 帰無仮説H0が正しいと仮定して、両側検定の棄却限界値の算出
lower = stats.binom.ppf(alpha/2, n, p0)
upper = stats.binom.ppf(1-alpha/2, n, p0)
print(f'棄却域:x < {lower:.3f}, x > {upper:.3f}')
# 棄却する/しないを判定
for sample in sample_list:
# 表の回数の集計
x = sum(sample)
x_result.append(x)
# 棄却の判定結果を格納(棄却されるTrue、棄却されないFalse)
test_result.append((x < lower) | (x > upper))
# 実験結果の表示
print(f'実験セット数{num_trials}回中、{sum(test_result)}回棄却')
plt.hist(x_result, ec='white')
plt.title(f'表の回数のヒストグラム\n実験セット数{num_trials}, 標本サイズ{n}, '
f'真の母比率{p}, 帰無仮説の母比率{p0}')
plt.axvline(lower, lw=0.5, ls='--', color='red', label='棄却限界値')
plt.axvline(upper, lw=0.5, ls='--', color='red')
plt.legend()
plt.show()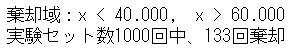
棄却限界値は 40回と60回です。
133セット分棄却されたようです。
13%の棄却率は、果たして高いのでしょうか・・・。
表が出た回数をヒストグラムで可視化しましょう。

正規分布のようなベル型の形状をしています。
確かに、正規分布近似していると言えそうです。
2本の赤い点線の棄却域と比べると、左側に偏っている感じがします。
「帰無仮説:表の出る確率は$${0.5}$$」と比べて、実際に表の出た回数の分布は、少ない方向に偏っています。
真の表の出る確率は$${0.45}$$ですので、少ない方向に偏るのは事実に即しているでしょう。
⑤正規分布で検定
続いて正規分布で検定します。
■正規分布で考える
標本データ sample_list の表の出る回数$${x}$$を標本サイズ$${n=100}$$で割った「標本比率$${\hat{p}}$$」を検定統計量にして検定します。
表の出る標本比率$${\hat{p}}$$の従う分布は、帰無仮説が正しいと仮定して設定します。
平均が帰無仮説の平均$${p_0=0.5}$$、標準偏差が$${\sqrt{p_0 (1-p_0)/n}=0.05}$$の正規分布$${N(0.5,0.05)}$$に従います。
■棄却限界値
「# 帰無仮説H0が正しいと仮定して、両側検定の棄却限界値の算出」で棄却限界値を算定しています。
正規分布$${N(0.5, 0.05)}$$の上側確率・下側確率それぞれ$${0.025}$$になる点を lower と upper に格納します。
lower と upper が棄却限界値になります。
■検定
「# 棄却する/しないを判定」で「表の出る標本比率$${\hat{p}}$$」が棄却域かどうかをチェックして、棄却する/棄却しないを判定します。
判定結果は test_result に格納します。
では、実行しましょう。
### 正規分布で検定
# 初期値設定
p_hat_result = []
test_result = []
ppf = stats.norm.ppf(1-alpha/2, 0, 1)
# 帰無仮説H0が正しいと仮定して、標準偏差、両側検定の棄却限界値の算出
stddev0 = np.sqrt(p0 * (1 - p0) / n)
lower = stats.norm.ppf(alpha/2, p0, stddev0)
upper = stats.norm.ppf(1-alpha/2, p0, stddev0)
print(f'棄却域:x_hat < {lower:.5f}, x_hat > {upper:.5f}')
# 棄却する/しないを判定
for sample in sample_list:
# 標本比率の算出
p_hat = sum(sample) / n
p_hat_result.append(p_hat)
# 棄却の判定結果を格納(棄却されるTrue、棄却されないFalse)
test_result.append((p_hat < lower) | (p_hat > upper))
# 実験結果の表示
print(f'実験セット数{num_trials}回中、{sum(test_result)}回棄却')
plt.hist(p_hat_result, ec='white')
plt.title(f'標本比率のヒストグラム\n実験セット数{num_trials}, 標本サイズ{n}, '
f'真の母比率{p}, 帰無仮説の母比率{p0}')
plt.axvline(lower, lw=0.5, ls='--', color='red', label='棄却限界値')
plt.axvline(upper, lw=0.5, ls='--', color='red')
plt.legend()
plt.show()
棄却限界値は 0.402(40.2回相当)と 0.598(59.8回相当)です。
183セット分棄却されたようです。
二項分布の棄却回数133セットと比べて、「50セット」棄却回数が多いことが分かりました。
1000セット中の50セットは$${5\%}$$。
この差は大きいような気がします。
表が出た標本比率をヒストグラムで可視化しましょう。

二項分布のヒストグラムと瓜二つ。
それもそのはず。
同一のコイントスデータを使っていますから。
ではなぜ、正規分布は棄却セット数が多かったのでしょう?
⑥二項分布と正規分布の違い
二項分布のケースと正規分布のケースの下側の棄却域に注目しましょう。
・二項分布:表の出た回数 < 40 回
・正規分布:表の出た比率 < 0.402( 回数換算で 40.2 回 )
表の出た回数が 40 回のセットの場合、
・二項分布のケースでは棄却されません。
・正規分布のケースでは棄却されます。

実際に、コイントスデータの中で表の出た回数が 40 回のセットをカウントしてみましょう。
counter = 0
for i in x_result:
if i==40:
counter += 1
counter
表の出た回数が 40回 のセットは、50 セットです。
二項分布と正規分布の棄却セット数の差と一致しました。
でも、50セットも棄却の誤差が出るのは気になります・・・・

⑦棄却域の再確認
実は、二項分布と正規分布の棄却域には「ズレ」があったのです。
二項分布を見ていきましょう。
二項分布の棄却限界値(棄却域の端)を取得します。
# 二項分布の棄却限界値を取得
stats.binom.interval(0.95, 100, 0.5)
下側が 40 回、上側が 60 回です。
小数点の無い、きっちりした整数に丸められています。
次に 40回 の下側確率を算出します。
cdf (累積分布関数)で取得できます。
# 二項分布の下側の棄却域(確率)を取得
stats.binom.cdf(40, 100, 0.5)
0.0284 です。
有意水準$${5\%}$$の半分に当たる 0.025 と比べると、0.0034 大きな値です。
棄却限界値が上側にずれているということです。
たった 0.0034 のズレが「40回」問題を引き起こして、棄却するセット数に影響したと考えられます。
上側も見てみましょう。
sf (生存関数)で上側確率を取得できます。
# 二項分布の上側の棄却域(確率)を取得
stats.binom.sf(60, 100, 0.5)
0.0176 です。
有意水準$${5\%}$$の半分に当たる 0.025 と比べると、0.0074 小さな値です。
棄却限界値が上側にずれているということです。
今回の実験では上側確率の影響は出ませんでしたが、実験条件次第では、上側確率のズレが検定の結果に影響するでしょう。
⑧連続修正
📕公式テキスト:3.4.4 母比率の推定(120ページ~)
二項分布の確率変数は「整数」のみの離散的な値をとります。
一方で、正規分布は小数を含む連続的な値をとります。
例えば、確率変数$${x}$$が$${5}$$の場合、正規分布では$${4.5 < x < 5.5}$$の範囲の確率で近似すると考えられます。
$${\pm0.5}$$と修正する方法を連続修正(イエーツの補正)と呼びます。
連続修正でどのくらい近似されるか確認しましょう。
正規分布の下側の棄却限界値を修正してみます。
まずは連続修正前。
# 正規分布の下側の棄却限界値 連続修正を行わない場合
stats.norm.cdf(40, loc=50, scale=5)
続いて連続修正後。
# 正規分布の下側の棄却限界値 連続修正を行う場合
stats.norm.cdf(40.5, loc=50, scale=5)
連続修正した棄却限界値は、「⑦棄却域の再確認」の二項分布の下側確率 0.0284 に近似しています。
今回の実験では、連続修正を行う方がよさそうです。
連続修正を行って正規分布の検定を実行しましょう。
### 正規分布で検定(連続修正)
# 初期値設定
p_hat_result = []
test_result = []
# 帰無仮説H0が正しいと仮定して、標準偏差、両側検定の棄却限界値の算出
stddev0 = np.sqrt(p0 * (1 - p0) / n)
lower = stats.norm.ppf(alpha/2, p0, stddev0)
upper = stats.norm.ppf(1-alpha/2, p0, stddev0)
print(f'棄却域:x_hat < {lower:.5f}, x_hat > {upper:.5f}')
# 棄却する/しないを判定
for sample in sample_list:
# 標本比率の算出
p_hat = (sum(sample) + 0.5) / n ### 連続修正 0.5を足す
p_hat_result.append(p_hat)
# 棄却の判定結果を格納(棄却されるTrue、棄却されないFalse)
test_result.append((p_hat < lower) | (p_hat > upper))
# 実験結果の表示
print(f'実験セット数{num_trials}回中、{sum(test_result)}回棄却')
plt.hist(p_hat_result, ec='white')
plt.title(f'標本比率のヒストグラム\n実験セット数{num_trials}, 標本サイズ{n}, '
f'真の母比率{p}, 帰無仮説の母比率{p0}')
plt.axvline(lower, lw=0.5, ls='--', color='red', label='棄却限界値')
plt.axvline(upper, lw=0.5, ls='--', color='red')
plt.legend()
plt.show()
「# 棄却する/しないを判定」で標本平均に +0.005 (※)を加算する連続修正を行っています。
結果として、棄却セット数は 133 回となり、二項分布の検定と一致しました!
やったね!
(※) 連続修正の補正値 0.5 ÷ 標本サイズ 100
⑨結論
1標本の母比率の検定で正規分布近似を利用する場合、「連続修正するほうが二項分布の確率に即した検定を行える可能性がある」ことを学びました。

実験は以上で終了いたします。
面白い結果を見ることができて、なんだか嬉しいです。
みなさんも、パラメータ設定の値をいろいろと変えてみて、実験を楽しんでください!

Pythonサンプルファイルのダウンロード
こちらのリンクからJupyter Notebook形式のサンプルファイルをダウンロードできます。
おわりに
細工されたコインを見破る方策の1つ、「コイントスの試行を多数行って1標本の母比率の検定(正規分布近似)すること」を学びました。
パソコンで擬似的にコイントスできれば良いのですが、リアルなコインを多数回トスするのはかなり大変そうです。
親指が痛くなるかな・・・

最後までお読みいただきまして、ありがとうございました。
のんびり統計シリーズの記事
次の記事
前の記事
目次
