
時系列分析入門【第3章 後編】線形モデル(OLS、GLS)、一般化線形モデル、線形混合モデルをPythonで実践する
この記事は、テキスト「RとStanではじめる 心理学のための時系列分析入門」の第3章「時系列の回帰分析」のRスクリプトをお借りして、Pythonで「実験的」に実装する様子を描いた統計ドキュメンタリーです。
取り扱いテーマは時系列回帰分析の応用編です。
線形回帰モデル:フーリエ級数項による季節成分の考慮
最小二乗法OLS、一般化最小二乗法GLSによる線形回帰
潜在成長曲線モデル:残差の系列相関の考慮
線形混合モデル(ランダム切片モデル、潜在成長曲線モデル)
中断時系列モデル:説明変数に時間軸を設定
線形回帰モデル、一般化線形モデルGLM(ポアソン回帰)
遂にテキストのコード・分析結果を再現できない分析手法が出現し始めました!
テキストの紹介、引用表記、シリーズまえがきは、このリンクの記事をご参照ください。
テキストで使用するデータは、R・Stan等のサンプルスクリプトで指定されています。
サンプルスクリプトは著者GitHubサイトからダウンロードして取得できます。
第3章 時系列の回帰分析
インポート
この章で用いるライブラリをインポートします。
### インポート
# 基本
import numpy as np
import pandas as pd
from scipy.linalg import toeplitz
# Rデータ読み取り
import rdata
# Rデータセット・一般化線形モデル・時系列分析
import statsmodels.api as sm
import statsmodels.formula.api as smf
from statsmodels.stats.stattools import durbin_watson
from statsmodels.tsa.seasonal import STL, seasonal_decompose
from statsmodels.tsa.stattools import adfuller
from statsmodels.tsa.deterministic import Fourier, DeterministicProcess
from statsmodels.graphics.tsaplots import plot_acf
# ARIMAモデル自動選択
import pmdarima as pm
# WEBアクセス
import requests
# グラフ描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'
# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')【補足】パッケージのインストール
利用環境に応じてパッケージをインストールしてください。
以下はインストールの参考コードです。
### インストール
## rdata
# anaconda
conda install -c conda-forge rdata
# pip
pip install rdata3.5 時系列同士の回帰分析
前編までに習得した分析手法を用いて回帰分析に取り組みます。
RのMARSSパッケージに含まれるLakeWashingtonデータセットを利用します。
32年間の水温(説明変数)とミジンコの量(目的変数)です。
① データの読み込み
WebサイトよりRデータ(rda形式)をダウンロードします。
### rdaデータのダウンロード
# 設定:ダウンロードファイルの格納先パス+ファイル名
filename = r'./lakeWAplankton.rda'
# ダウンロードの実行
url = r'https://github.com/cran/MARSS/blob/master/data/lakeWAplankton.rda?' \
'raw=true'
res = requests.get(url)
with open(filename, mode='wb') as f:
f.write(res.content)続いて、rdataパッケージを用いてrdaファイルをpandasのデータフレームに読み込みます。
rdaファイルに格納されたデータはxarray形式です。
取り出し方法を見つけるのに時間がかかりました・・・。
### lakeWAplankton Rdataの読み込み https://pypi.org/project/rdata/
# ファイルの読み込み・解析
parsed = rdata.parser.parse_file(filename)
# データの変換:辞書型(中のデータ形式はxarray)
converted = rdata.conversion.convert(parsed)
# 列名の取得
col = converted['lakeWAplanktonTrans'].coords.variables['dim_1'].data
# データフレーム化
plank_df_orgn = pd.DataFrame(converted['lakeWAplanktonTrans'].data, columns=col)
display(plank_df_orgn)【実行結果】
年:Yearと月:Monthが別々の列に格納されています。
水温:Tempとミジンコ:Cyclopsを利用します。

② データの前処理
利用期間1980年~1990年を抽出して、さらに、年月を日付に変換してTime列を生成します。
# 1980年から1990年までのデータを抽出
plank_df = plank_df_orgn[plank_df_orgn['Year'].isin(range(1980, 1991))]\
.reset_index(drop=True)
# 日付Timeを設定
plank_df['Time'] = plank_df.apply(lambda x: pd.to_datetime(
str(int(x['Year']*10000 + x['Month']*100 + 1))
), axis=1)
display(plank_df[['Time', 'Temp', 'Cyclops']])【実行結果】
データが整いました。

③ データのプロット
時間とミジンコ、時間と水温の2つの折れ線グラフを描画します。
テキストの図3.9に相当します。
# 描画 ※図3.9に相当
xcol = 'Time'
ycols = ['Cyclops', 'Temp']
fig, ax = plt.subplots(1, 2, figsize=(10, 4), sharey=True)
for i in range(len(ycols)):
ax[i].plot(plank_df[xcol], plank_df[ycols[i]])
ax[i].set(xlabel=xcol, ylabel=ycols[i])
ax[i].grid()
plt.tight_layout();【実行結果】
右側の水温にはおそらく12ヶ月周期の季節性がありそうです。
左側のミジンコ量も、おそらく水温と連動した周期性がありそうです。
両方とも分散が大きく変化することは無さそうです。

④ ADF検定
データが単位根過程かどうかを確認します。
帰無仮説は「単位根を持つ」です。
statsmodelsのadf_testを用いて、ADF検定用の関数を定義します。
# ADF検定関数の定義
def adf_test(x, regression='ct', maxlag=5, autolag='AIC'):
result = adfuller(x=x, # テスト対象データ
regression=regression, # 定数項とトレンド項を含めるかどうか
maxlag=maxlag, # ラグの最大次数
autolag=autolag, # ラグ次数の選択規準
)
print(f'ADF({result[2]}): {result[0]:.3f}, p値: {result[1]:.3f}')
print('棄却限界値')
for k, v in result[4].items():
print(f' {k:5s}: {v:.3f}')
return result水温のADF検定です。
### ADF検定 帰無仮説「単位根を持つ」
# Temp:水温
result = adf_test(x=plank_df['Temp'], # テスト対象データ
regression='ct', # 定数項とトレンド項を含める
maxlag=4, # ラグの最大次数は4
autolag='AIC' # ラグ次数はAICで選択
)【実行結果】
p値は$${0.000}$$。有意水準5%で有意であり、単位根過程ではないと言えます。

続いてミジンコの量です。
# Cyclops:ミジンコ ※テキストの結果と若干異なる
result = adf_test(x=plank_df['Cyclops'], # テスト対象データ
regression='ct', # 定数項とトレンド項を含める
maxlag=4, # ラグの最大次数は4
autolag='AIC' # ラグ次数はAICで選択
)【実行結果】
p値は$${0.000}$$。有意水準5%で有意であり、単位根過程ではないと言えます。

⑤ 季節成分を考慮しないOLS回帰
残差の自己相関を確認する目的で線形単回帰分析を行います。
statsmodelsのolsを利用します。
# 季節成分を考慮しないOLS回帰 statsmodelsのformula API
fit1 = smf.ols(formula='Cyclops ~ Temp ', data=plank_df).fit()
print(fit1.summary())【実行結果】
ダービン-ワトソン比(Durbin-Watson)は$${0.729}$$。
残差に系列相関がありそうです。

残差の自己相関関数をプロットします。
statsmodelsのplot_acfを用いて、残差fit1.residの自己相関を描画します。
テキストの図3.10に相当します。
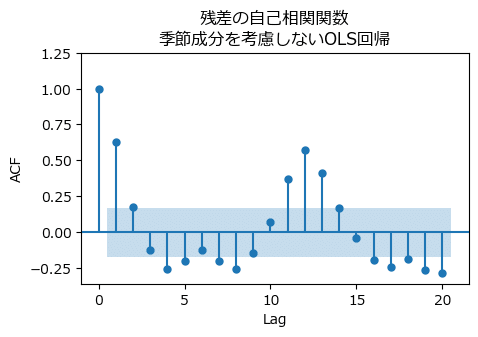
# 自己相関関数の描画 ※図3.10に相当
fig, ax = plt.subplots(figsize=(5, 3))
plot_acf(fit1.resid, lags=20, auto_ylims=True, ax=ax,
title='残差の自己相関関数\n季節成分を考慮しないOLS回帰')
ax.set(xlabel='Lag', ylabel='ACF');【実行結果】
ラグ12の自己相関係数(ACF)が0.5を超えています。
残差に周期12の季節成分があることを確認できました。
OLS(最小二乗法)による回帰分析では太刀打ちできません。。。
⑥ 季節成分を考慮したOLS回帰
テキストでは「フーリエ級数展開」という手法を用いて季節成分を表現し、OLS回帰を実行しています。
Rはharmonic関数でフーリエ級数項を追加できるようです。
Pythonでは、次のサイトの情報を参考にして、フーリエ級数を算出しました。
ありがとうございます!
フーリエ級数をデータフレームに追加します。
statsmodels の Fourier と DeterministicProcess を利用します。
### 季節成分を考慮したOLS回帰
## フーリエ級数の算出
fourier = Fourier(order=2, period=12) # 次数2,周期12のフーリエ級数
dp = DeterministicProcess(index=plank_df['Time'].dt.month, # データ項目「月」
constant=False, # 定数項なし
order=0, # 次数なし
drop=True, # 多重共線性関連?
additional_terms=[fourier]) # 定義したフーリエ級数
harmonic = dp.in_sample().reset_index(drop=True)
## データフレームの整理
# フーリエ級数変数の列名変更
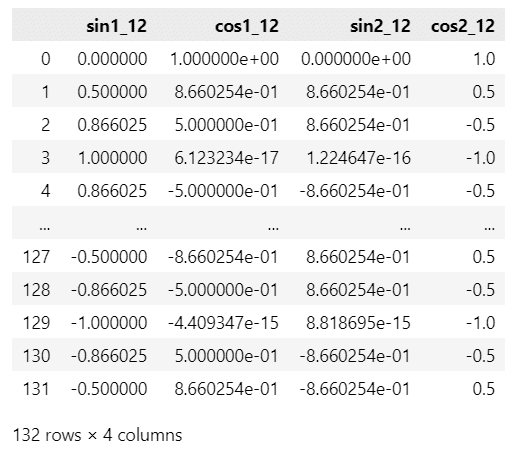
harmonic.columns = ['sin1_12', 'cos1_12', 'sin2_12', 'cos2_12']
display(harmonic)
# plank_dfとフーリエ級数変数を結合
plank_df = pd.concat([plank_df, harmonic], axis=1)
display(plank_df)【実行結果】
上の表がフーリエ級数です。
2つのsin・cosの組み合わせができています。

フーリエ級数項「sin1_12~cos2_12」を加えたOLS回帰を実行します。
### OLS実行 ※テキストの結果に近い。しかしフーリエ級数変数の傾きは全く一致しない
fit2 = smf.ols(formula='Cyclops ~ Temp + sin1_12 + cos1_12 + sin2_12 + cos2_12',
data=plank_df).fit()
print(fit2.summary())【実行結果】
切片(Intercept)とTempの回帰係数はテキストとほぼ同じ値になりました。
Tempの回帰係数のp値は$${0.079}$$であり、有意水準10%で有意、有意水準5%で有意ではない、というレベルです。
ただ、ダービン-ワトソン比(Durbin-Watson)は$${0.952}$$であり、系列相関無しの基準値「2」から離れているため、残差の系列相関がありそうな状況です。

残差の自己相関関数をプロットします。
テキストの図3.11に相当します。
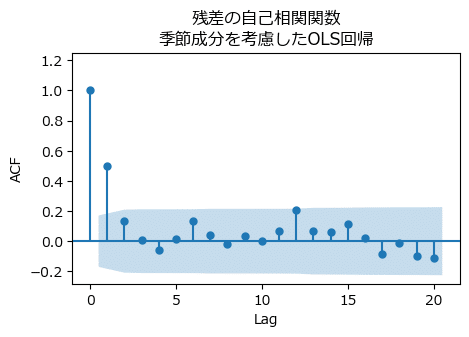
# 自己相関関数の描画 ※図3.11に相当
fig, ax = plt.subplots(figsize=(5, 3))
plot_acf(fit2.resid, lags=20, bartlett_confint=False, auto_ylims=True, ax=ax,
title='残差の自己相関関数\n季節成分を考慮したOLS回帰')
ax.set(xlabel='Lag', ylabel='ACF');【実行結果】
ラグ1の系列相関が高いようです。
⑦ 季節成分を考慮したGLS回帰
前回記事の「3.3.3 一般化最小二乗法」と同様に、PythonのGLS関連モジュールに、AR(1)過程に従う残差の分散共分散行列を指定できるものを見つけることができず、(是非はともかく)、statsmodels公式サイトのコードを利用しています。
GLSのコード例・実行結果がテキストと一致しないことを前提にしてご覧ください。
### 季節成分を考慮したGLS回帰
# ※テキストの結果と微妙にずれている。またフーリエ級数の係数はテキストと合致していない
## パラメータsigma(分散共分散行列)の取得
# ar1_smのOLS残差の1階階差系列をさらにOLS、最小二乗基準を最小化する線形係数ρを取得
res_fit = sm.OLS(fit2.resid[1:].values, fit2.resid[:-1].values).fit()
rho = res_fit.params
# 分散共分散行列に変換
order = toeplitz(np.arange(len(plank_df))) # scipy.linalgのtoeplitz
sigma = rho**order
## 一般化最小二乗法による回帰分析の実行
fit3 = smf.gls(formula='Cyclops ~ Temp + sin1_12 + cos1_12 + sin2_12 + cos2_12',
data=plank_df, sigma=sigma).fit()
# GLS回帰分析の結果表示
print(fit3.summary())【実行結果】
水温Tempの回帰係数のp値は$${0.008}$$です。
有意水準5%で有意な回帰係数ということになり、水温がミジンコの量に関係している可能性を示唆しています。

最後にGLS回帰によるミジンコの量の予測値を描画してみます。
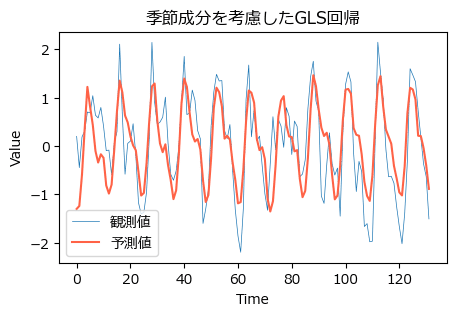
### GLS回帰の結果をプロット
fig, ax = plt.subplots(figsize=(5, 3))
# ミジンコの量の観測値の描画
plt.plot(plank_df['Cyclops'], lw=0.5, label='観測値')
# ミジンコの量の予測値の描画
plt.plot(fit3.fittedvalues, color='tomato', label='予測値')
# 修飾
ax.set(title='季節成分を考慮したGLS回帰', xlabel='Time', ylabel='Value')
ax.legend();【実行結果】
GLS回帰の予測値は、観測値よりも値の幅が小さいですが、周期性はほぼ一致しているようです。
3.6 潜在成長曲線モデル
さて、私の限界を超えるモデルが登場です。
完コピできていないことを告白いたします(泣)
ひとまず「試したこと」を掲載します。
キーワードは #パネルデータ #マルチレベル分析 #階層線形モデル #混合効果モデル #潜在成長曲線モデル です
① データの読み込み
Rのnlmeパッケージのデータセット「BodyWeight」を読み込み、Rスクリプトと同様の前処理を実施します。
## データセットの準備
# 第1引数:Item, 第2引数:Package
# BodyWeightデータセットの読み込み
df = sm.datasets.get_rdataset('BodyWeight', 'nlme').data
# 前処理
df = df[(df['Diet'].isin((1, 2))) & ~(df['Time']==44)]
df['Time'] = (df['Time'] - 1) / 7
# 前処理後のデータの表示
display(df)【実行結果】
Ratはラットの個体番号、Dietは餌の種類(1か2)、timeは体重の測定時点(週)、weightは体重です。

② データのプロット
seabornのlineplotでラット個体別(hueで指定)の折れ線グラフを描画します。餌Dietごとに線種を変えています(styleで指定)。
また、凡例をグラフの外に出す目的で、legendの引数に bbox_to_anchor=(1, 1) を設定しています。
### 描画 ※図3.14に相当
plt.figure(figsize=(8, 3))
sns.lineplot(data=df, x='Time', y='weight', hue='Rat', style='Diet', lw=1)
plt.legend(bbox_to_anchor=(1, 1))
plt.grid(lw=0.5);【実行結果】
餌2(点線)のラットのほうが体重が大きいようです。

③ ランダム切片モデル
このモデルは時間を考慮しないマルチレベル分析ですが、潜在成長曲線モデルでは無いそうです。
テキストの数式等をお借りします。
時点$${t}$$における個体$${i}$$の体重の観測値を目的変数$${Y_{it}}$$とします。
【ランダム切片モデル】
$$
\begin{align*}
Y_{it} &= \beta_{0i} + R_{it}, \quad R_{it} \sim \text{Normal}(0, \sigma^2_R) \\
\beta_{0i} &= \gamma_{00} + U_{0i}, \quad U_{0i} \sim \text{Normal}(0, \sigma^2_U) \\
\end{align*}
$$
$${U_{0i}}$$:ランダム効果(時間で変動しない個体差)
$${\gamma_{00}}$$:固定効果であり切片
$${R_{it}}$$:誤差
statsmodelsの線形混合モデル「mixedlm」を利用します。
statsmodels公式サイトの線形混合効果モデルの例示を手がかりにしてコードを描いてみます。
statsmodelsのformula APIでmixedlmのモデル記述をしています。
### ランダム切片モデル ※おそらくテキストの結果を再現できている
rand_res = smf.mixedlm(formula='weight ~ 1', groups='Rat', data=df).fit()
print(rand_res.summary())【実行結果】
テキストが利用するRのnlmeパッケージの出力結果とフォーマットは異なっています。
切片(Intercept)の$${337.008}$$は、テキストの「固定」切片と一致しています。

ランダム切片モデルのランダム効果のバラツキ$${\sigma^2_U}$$、誤差$${\sigma^2_R}$$、固定効果$${\gamma_{00}}$$を確認しましょう。
線形混合モデルの出力結果「rand_res」から情報を取り出します。
# 個体間のばらつきσ_U、測定期間内のばらつきσ_Rの計算
# 計算
sigma_U = pd.Series(rand_res.random_effects).std() # ランダム効果:random_effects
sigma_R = rand_res.resid.std() # 誤差:resid
gamma_00 = rand_res.fe_params.values[0] # 固定効果:fe_params
# 表示
print(f'個体間のばらつきσ_U:{sigma_U:8.3f} g')
print(f'期間内のばらつきσ_R:{sigma_R:8.3f} g')
print(f'固定効果 γ_00:{gamma_00:8.3f} g')【実行結果】
テキスト95ページの各値と一致できています。
おそらく、statsmodelsでうまくモデル記述できていると思います。

ラットの個体ごとのランダム効果$${U_{0i}}$$を見てみましょう。
ランダム効果の結果rand_resに対して、random_effectsを指定します。
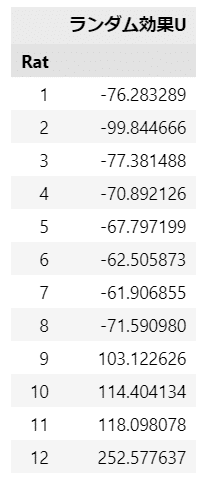
### ランダム効果の内容を確認
re_df = pd.DataFrame(rand_res.random_effects).T.set_axis(['ランダム効果U'],
axis=1)
re_df.index.name='Rat'
display(re_df)【実行結果】
切片$${337g}$$に対して$${-99.8}$$から$${252.6}$$まで幅広くばらついています。
④ 潜在成長曲線モデル(残差の系列相関を考慮しない)
いよいよ、テキストのモデルに関するPython実装方法が分からない領域に踏み込みます。
ひとまず、テキストの数式をお借りします。
【潜在成長曲モデル(残差の系列相関を考慮しない)】
$$
\begin{align*}
Y_{it} &= \beta_{0i} + \beta_{1i} X_{it}+ R_{it}, \quad R_{it} \sim \text{Normal}(0, \sigma^2_R) \\
\beta_{0i} &= \gamma_{00} + \gamma_{01} Z_i + U_{0i} \\
\beta_{1i} &= \gamma_{10} + \gamma_{11} Z_i + U_{0i} \\
\left(\begin{matrix} U_{0i} \\ U_{1i} \end{matrix} \right) &=\text{Normal}\left[ \left( \begin{matrix}0 \\ 0 \end{matrix} \right),\left( \begin{matrix}\tau^2_{00} & \tau_{01} \\\tau_{01} & \tau^2_{11} \\\end{matrix}\right)\right]
\end{align*}
$$
statsmodels公式サイトの線形混合効果モデルの例示を手がかりにしてコードを描いてみます。
適否は不明です。。。
### 残差の系列相関を考慮しない潜在成長曲線モデル
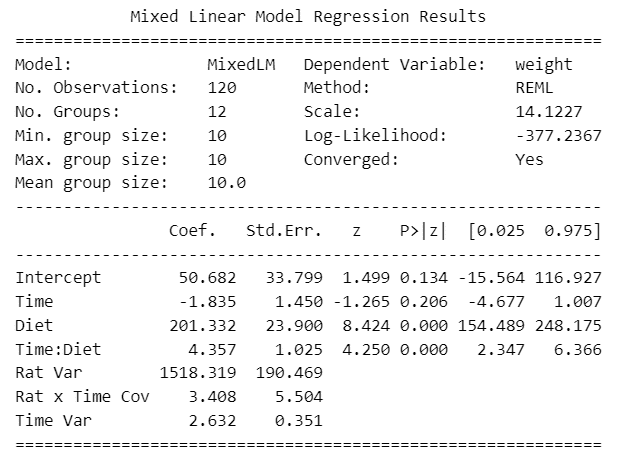
fit1_res = smf.mixedlm(formula='weight ~ Time*Diet', groups='Rat',
re_formula='~Time', data=df).fit()
print(fit1_res.summary())【実行結果】
テキストの実行結果と合致しているかどうか、よく分かっていません。
係数のp値はTimeが$${0.206}$$で有意でない感じ、Dietが$${0.000}$$で有意である感じです。
以下はRサンプルコードから取得した「fit1」のサマリー表示です。

2つの出力結果を比べてみます。
対数尤度Log-Likelihoodの値が、テキストのRモデルとPythonのmixedlmモデルの両方で$${-377.2367}$$となり、一致します。
また、Rの固定効果のDiet2とTime:Diet2の値は、mixedlmのDietとTime:Dietの係数(coef)と一致します。
その他の項目については、Rの出力の仕方とmixedlmの出力の仕方が異なるため、簡単に比較できません。。。残念です。
ひとまず、残差の自己相関関数を描画します。
テキストの図3.16に相当します。
# 自己相関関数の描画 ※図3.16に相当
fig, ax = plt.subplots(figsize=(5, 3))
plot_acf(fit1_res.resid, lags=10, auto_ylims=True, ax=ax, alpha=0.01,
title='fit1 残差の自己相関')
ax.set(xlabel='Lag', ylabel='ACF');【実行結果】
テキストではラグ3に若干の系列相関が見られますが、下の図では系列相関が見当たりません。。。

⑤ 【別案】潜在成長曲線モデル(残差の系列相関を考慮しない)
一般化線形混合モデルを取り扱うPythonの別のパッケージ「GPBoost」を試してみました。
■ インストール
### GPBoostのインストール
# 前提:setuptoolsがインストール済みであること
pip install setuptools
pip install gpboost -U■ インポート
### 追加インポート
import gpboost as gpb
from patsy import dmatrix■ モデルの構築と学習
### モデルの構築と学習
## データの準備
# データフレームの型をintに統一
df_gpb = df.astype('int')
## GPBoost
# 各種設定
group = df_gpb['Rat']
y = df_gpb['weight']
X = dmatrix('~ Time*Diet', data=df_gpb)
# モデルの定義
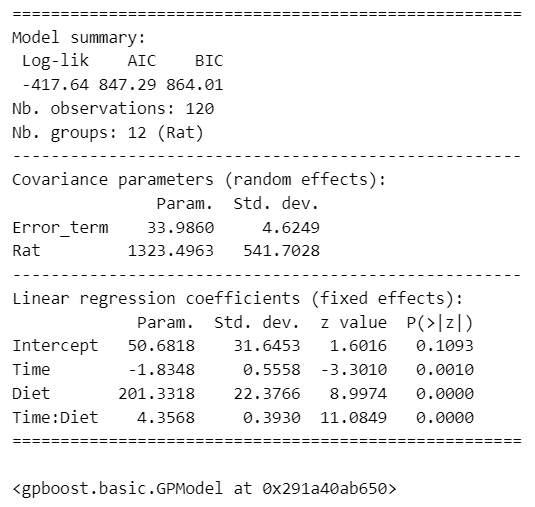
gp_model = gpb.GPModel(group_data=group, likelihood='gaussian')
# モデルのフィット
gp_model.fit(y=y, X=X, params={'std_dev':True})
# サマリーの表示
gp_model.summary()【実行結果】
固定効果の線形回帰係数(coefficients)はstatsmodelsのmixedlmの結果とほぼ同じです。
⑥ 潜在成長曲線モデル(残差の系列相関を考慮する)
Rのlmeで誤差の共分散行列構造を指定する「corAR1(form=~Time|Tat)」について、statsmodelsやGPBoostでの実装方法が分かりませんでした。
ですので、このモデルに関してはテキストの完コピを諦めます。
次のコードではstatsmodelsの分散設定例を参考にして、Timeを分散成分に指定してみました。(vc_formula引数で分散成分を指定しています)
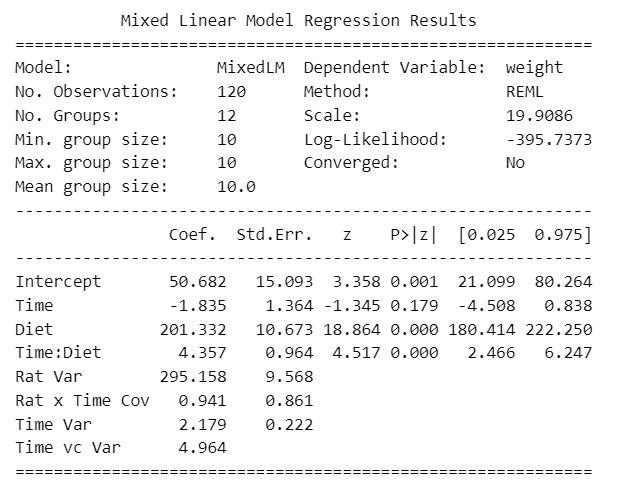
### 残差の系列相関を考慮した?潜在成長曲線モデル
vc = {'Time vc': '0 + C(Time)'}
fit2_res = smf.mixedlm(formula='weight ~ Time*Diet', groups='Rat',
re_formula='Time', vc_formula=vc, data=df).fit()
print(fit2_res.summary())【実行結果】
結果はおそらく不適切だと思います。
係数が残差の系列相関を考慮しないモデルとほぼ同じですので。
では気を取り直して、新しいモデルに移りましょう!
3.7 中断時系列デザイン
シチリア島で実施された「公共施設内の禁煙ルール施行(介入)」前後の月別「心臓疾患入院患者数」データを利用して、中断時系列分析を行います。
テキストよりモデルの数式をお借りします。
$${Y_t = \beta_0 + \beta_1 T + \beta_2 X_t + \beta_3 T X_t}$$
$${Y_t:観測値}$$
$${T:時間,}$$
$${X_t:時点tでの介入の有無(0:無し、1:有り) }$$
$${\beta_0:切片}$$
$${\beta_1:ベースライン期間(介入の無い期間)のトレンド(傾き)}$$
$${\beta_2:介入によるレベル変化}$$
$${\beta_3:介入によるトレンド変化}$$
長い式ですが、介入$${X_t}$$のとる値は0か1なので、介入の有無により式が次のように切り替わります。
説明変数が時間$${times}$$のシンプルな回帰式です。
■ 介入無し:
$${目的変数 = 切片 + 傾き \times 時間}$$
■介入有り:
$${目的変数 = 切片1 + 傾き1 \times 時間 + 切片2 + 傾き2 \times 時間}$$
$${\Leftrightarrow 目的変数 = (切片1 + 切片2) + (傾き1 + 傾き2) \times 時間}$$
このモデルは一般化線形モデル(GLM)で分析できるので、私の実力値(低い(泣))でなんとか対応できそうです。
statsmodelsを利用して頑張ります!
① データの読み込み
Webサイトよりデータの読み込みを行います。
### データの読み込み
# データをダウンロードしてpandasのデータフレームに格納
url = r'https://raw.githubusercontent.com/gasparrini/' \
r'2017_lopezbernal_IJE_codedata/master/sicily.csv'
data = pd.read_csv(url)
# データの表示
print('data.shape:', data.shape)
display(data.head())【実行結果】
項目の内容は次のとおりです。
year:年、month:月、aces:患者数、time:通算月数、smokban:禁煙ルール施行有無、pop:シチリア島の人口、stdpop:年齢調整後人口
介入にあたるsmakban:禁煙は2005年1月から実施されています。

② 線形回帰モデル:介入×時間モデル
禁煙介入smokbanと時間timeの交互作用を考慮するモデルです。
glmよりも分析結果の情報が多いstatsmodelsのols(最小二乗法)を利用します。
formulaで定義した式の完成イメージは次のとおりです。
$${aces = Intercept + 係数1 \times smokban + 係数2 \times time + 係数3 \times smokban \times time}$$
### 線形回帰モデル 介入✕時間モデル
# 傾きの変化を考慮したモデル
# 最小二乗法による回帰 statsmodelsのformula API
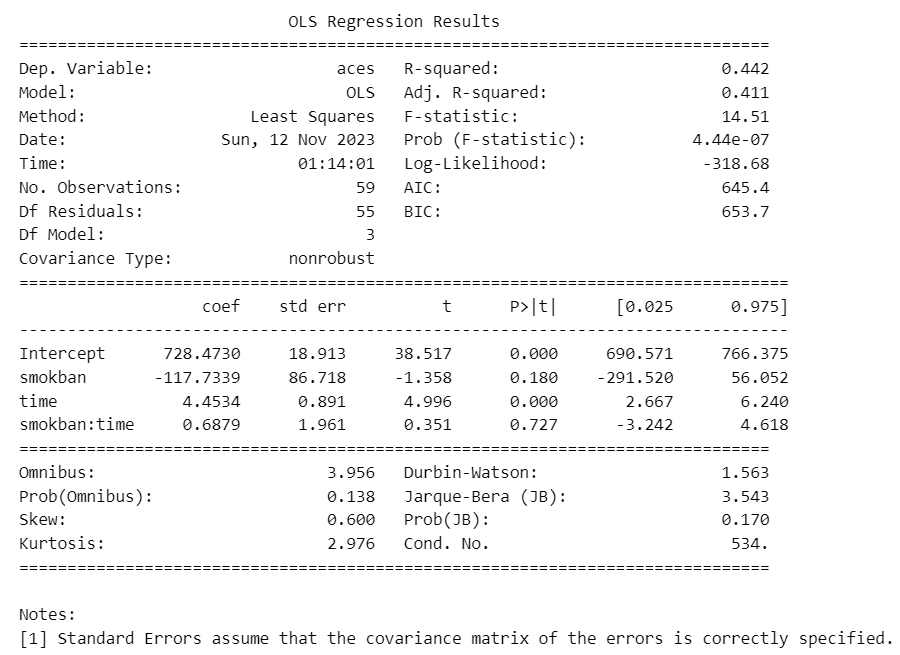
fit1 = smf.ols(formula='aces ~ smokban * time', data=data).fit()
print(fit1.summary())【実行結果】
回帰係数はテキストと同じになりました。
回帰式は次のようになります。
$${Y_t = 728.4730 - 117.7339 \times smokban + 4.4534 \times time + 0.6879 \times smokban \times time}$$
禁煙の効果を示すsmokbanの回帰係数のp値は$${0.180}$$であり、有意水準5%で有意でない=禁煙の効果が有意でない、という分析結果です。
予測値と残差の自己相関関数を可視化します。
テキストの図3.18に相当します。
同じ描画を繰り返し利用するので、描画関数 fit_plot を定義しました。
### 描画 ※図3.18に相当
# 描画関数の定義
def fit_plot(pred, resid, addtext):
fig, ax = plt.subplots(1, 2, figsize=(8, 3))
# 患者数の時系列プロット+回帰分析による予測値のプロット
ax[0].scatter(data.index, data['aces'], s=5, label='観測値')
ax[0].plot(pred, label='予測値', color='tomato')
ax[0].set(ylim=(0, 1050), xlabel='Time', ylabel='ACEs', title='患者数の推移')
ax[0].legend()
# 残差の自己相関関数のプロット
plot_acf(resid, lags=20, auto_ylims=True, ax=ax[1],
title=f'{addtext}:残差の自己相関関数')
ax[1].set(xlabel='Lag', ylabel='ACF')
# 修飾
plt.tight_layout()
plt.show()
# 描画の実行
fit_plot(fit1.fittedvalues, fit1.resid, 'fit1')【実行結果】
残差の自己相関関数は6か月・12か月の周期的な系列相関があることを示しています。

③ 線形回帰モデル:介入×時間+季節成分モデル
前のモデルに12か月周期の季節成分を加えるモデルです。
季節成分はフーリエ級数項で表現します。
「3.5」のミジンコの量の分析で用いたフーリエ級数項の算出方法を利用します。
### 線形回帰モデル 介入✕時間+季節成分モデル
## フーリエ級数の算出
fourier = Fourier(order=2, period=12)
dp = DeterministicProcess(index=plank_df['Time'].dt.month,
constant=False,
order=0,
drop=True,
additional_terms=[fourier])
harmonic = dp.in_sample().reset_index(drop=True)
## データフレームの整理
# フーリエ級数変数の列名変更
harmonic.columns = ['sin1_12', 'cos1_12', 'sin2_12', 'cos2_12']
display(harmonic)
# dataとフーリエ級数変数を結合
data_mod = data.copy()
data_mod = pd.concat([data_mod, harmonic], axis=1)
# display(data_mod)【実行結果】
フーリエ級数項を表示しました。

OLSを実行します。
### 最小二乗法による回帰 statsmodelsのformula API ※テキストの結果に近い
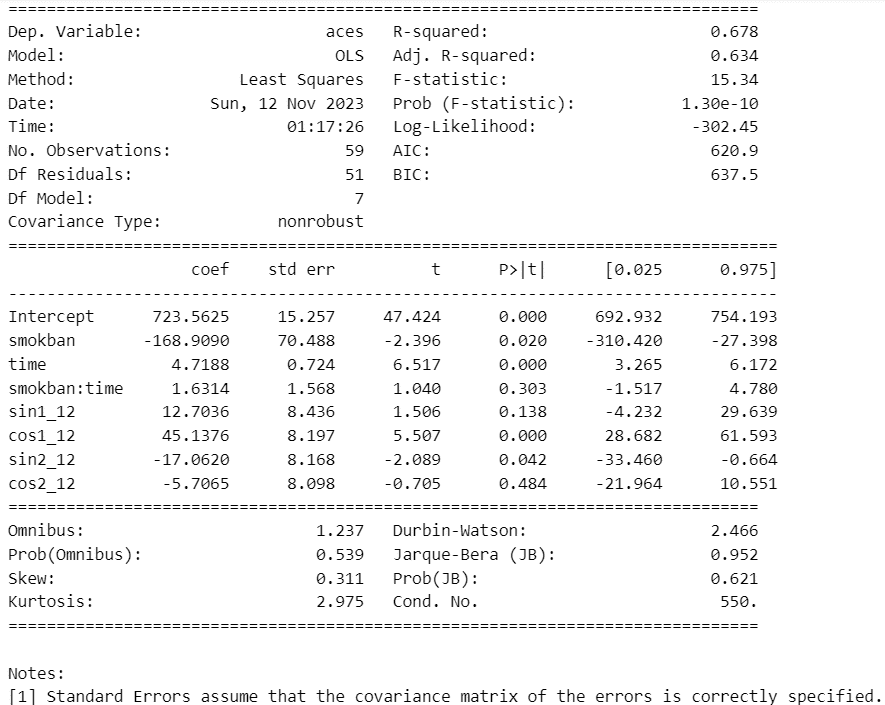
fit2 = smf.ols(formula='aces ~ smokban*time + sin1_12+cos1_12+sin2_12+cos2_12',
data=data_mod).fit()
print(fit2.summary())【実行結果】
切片、smokban・time・smokban:timeの回帰係数はテキストと同じになりました。
回帰式は次のようになります。季節成分は省略しています。
$${Y_t = 723.5625 - 168.9090 \times smokban + 4.7188 \times time + 1.6314 \times smokban \times time + 季節成分の効果}$$
ダービン‐ワトソン比(Durbin-Watson)は$${2.466}$$であり、残差の系列相関が無い「2」に近くなりました。
禁煙の効果を示すsmokbanの回帰係数のp値は$${0.020}$$であり、有意水準5%で有意=禁煙の効果が有意であるという分析結果になりました。
予測値と残差の自己相関関数を可視化します。
テキストの図3.19に相当します。
### 描画 ※図3.19に相当
fit_plot(fit2.fittedvalues, fit2.resid, 'fit2')【実行結果】
前のモデルと比べると、予測値の線は観測値に沿っている感じです。
残差の自己相関関数は青い領域に収まっており、系列相関はほぼ無さそうな感じです。

④ ポアソン回帰モデル:介入×時間モデル
確率分布にポアソン分布、リンク関数に対数リンク関数を用いたポアソン回帰モデルに移ります。
観測値である患者数は0以上の整数値をとるカウントデータということで、正規分布よりもポアソン分布の方が適切だろう、ということのようです。
テキストの式をお借りします。
$${\log(\lambda_t)=\beta_0 + \beta_1 \times smokban + \beta_2 \times time + \beta_3 \times smokban \times time}$$
$${\Leftrightarrow E[Y_t] = \lambda_t = \exp(\beta_0 + \beta_1 \times smokban + \beta_2 \times time + \beta_3 \times smokban \times time)}$$
statsmodelsのglsを利用します。
ポアソン分布の指定は「family=sm.families.Poisson()」で行います。
ポアソン分布を指定する場合、デフォルトで「対数リンク関数」を適用するので、リンク関数の指定を省略できます。
### 一般化線形モデル(ポアソン回帰) 介入✕時間
# GLMによるポアソン回帰 statsmodelsのformula API
fit3 = smf.glm(formula='aces ~ smokban * time', data=data,
family=sm.families.Poisson()).fit()
print(fit3.summary())【実行結果】
回帰式は次のようになります。
$${E[Y_t] = \exp(6.5948 - 0.1294 \times smokban + 0.0055 \times time + 0.0005 \times smokban \times time)}$$

予測値と残差の自己相関関数を可視化します。
テキストの図3.20に相当します。
### 描画 ※図3.20に相当
fit_plot(fit3.fittedvalues, fit3.resid_response, 'fit3')【実行結果】
予測値は線形回帰(正規分布)と近い結果です。
残差の自己相関は、ラグ6か月・12ヶ月に若干の系列相関がみられます。

⑤ ポアソン回帰モデル:介入×時間+季節成分モデル
前のモデルに12か月周期の季節成分を加えるモデルです。
季節成分には③の線形回帰モデルで作成したフーリエ級数項を利用します。
### 一般化線形モデル(ポアソン回帰) 介入✕時間+季節成分
# GLMによるポアソン回帰 statsmodelsのformula API
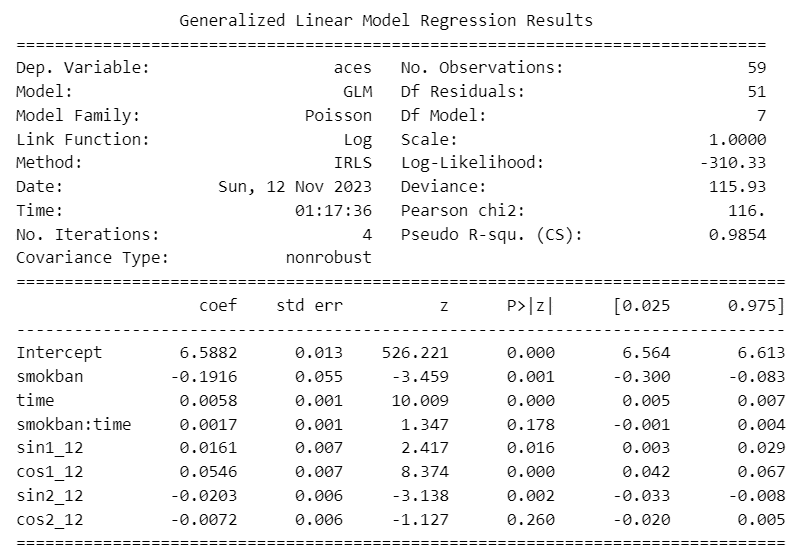
fit4 = smf.glm(formula='aces ~ smokban*time + sin1_12+cos1_12+sin2_12+cos2_12',
data=data_mod, family=sm.families.Poisson()).fit()
print(fit4.summary())【実行結果】
回帰式は次のようになります。季節成分は省略しています。
$${E[Y_t] = \exp(6.5882 - 0.1916 \times smokban + 0.0058 \times time + 0.0017 \times smokban \times time) + 季節成分の効果}$$
予測値と残差の自己相関関数を可視化します。
### 描画
fit_plot(fit4.fittedvalues, fit4.resid_response, 'fit4')【実行結果】
季節成分を考慮した線形回帰モデルのグラフと似た結果になりました。

⑥ ポアソン回帰モデル:オフセット項+介入×時間+季節成分モデル
患者発生率$${E\left[ \cfrac{Y_t}{人口_t}\right]}$$を分析対象にします。
ポアソン分布は0以上の整数値しか取らないため、小数値の可能性がある「率」を目的変数にすることが難しいようです。
また、観測値を観測値で割り算すると観測値自体の情報(値の大きさなど)が失われてしまうので、割り算は避けるべき、とされています。
「率」に関心のある場合には、オフセット項【$${\log(人口_t)}$$】を導入します。
テキストの式をお借りします。
$${\log \left( E \left[ \cfrac{Y_t}{人口_t} \right] \right) = \beta_0 + \beta_1 \times smokban + \beta_2 \times time + \beta_3 \times smokban \times time}$$
$${\Leftrightarrow \log(E[Y_t]) = \log(人口_t) + \beta_0 + \beta_1 \times smokban + \beta_2 \times time + \beta_3 \times smokban \times time}$$
次のリンクのpdf資料がオフセット項の理解に役立ちました。
ありがとうございます!
【なんでも “割算” するな! - GLM の工夫】 6ページのシート29/46~
statsmodelsのglmでのオフセット項は、引数で「offset=np.log(data_mod['stdpop'])」を指定します。
年齢調整後人口stdpopを用います。
### 一般線形モデル(ポアソン回帰) オフセット項+介入✕時間+季節成分
# オフセット項におく対数変数の意味が記載されている参考資料
# https://kuboweb.github.io/-kubo/stat/2015/ngt5/HOkubo2015ngt5.pdf
# GLMによるポアソン回帰 statsmodelsのformula API
fit5 = smf.glm(formula='aces ~ smokban*time + sin1_12+cos1_12+sin2_12+cos2_12',
offset=np.log(data_mod['stdpop']), data=data_mod,
family=sm.families.Poisson()).fit()
print(fit5.summary())【実行結果】
回帰式は省略します(オフセット項の記述方法が分からず・・・)。
患者発生率についても、禁煙smokbanの回帰係数のp値は0.05未満であり、禁煙効果が有意であるとの結果になりました。

予測値と残差の自己相関関数を可視化します。
テキストの図3.21に相当します。
### 描画 ※図3.21に相当
fit_plot(fit5.fittedvalues, fit5.resid_response, 'fit5')【実行結果】

テキストのモデルは以上で終了です。
引き続きアディショナルタイムをお楽しみ下さい。

⑦ 続・ポアソン回帰モデル:オフセット項+介入×時間+季節成分モデル
statsmodelsのポアソン回帰専用の関数「poisson」を使ってみます。
予測値等の単位は$${\log(発生率)}$$になるので注意が必要です。
# おまけ:ポアソン回帰 statsmodelsのformula API
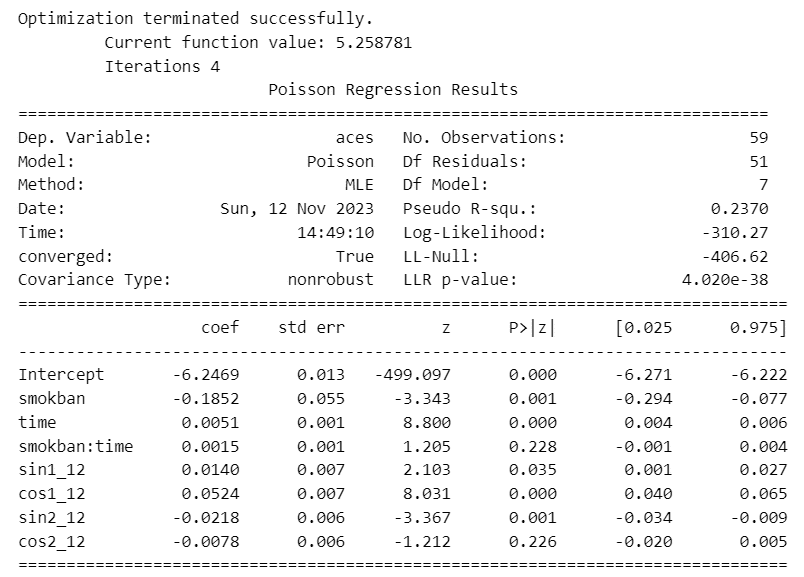
fit6 = smf.poisson(formula='aces ~ smokban*time + sin1_12+cos1_12+sin2_12+cos2_12',
offset=np.log(data_mod['stdpop']), data=data_mod,).fit()
print(fit6.summary())【実行結果】
予測値と誤差の自己相関関数を描画します。
$${\log(発生率)}$$の予測値「fit6.fittedvalues」に逆関数を適用して$${\exp(\log(発生率))}$$とすることで、発生率を得ています。
### 予測値(発生率)と残差の自己相関関数の描画
# 予測値はlog(発生率)である ⇒ exp(予測値)とすることで発生率を得られる。
fig, ax = plt.subplots(1, 2, figsize=(8, 3))
# 患者発生率の時系列プロット+ポアソン回帰による予測値のプロット
ax[0].scatter(data.index, data['aces'] / data['stdpop'], s=5, label='観測値')
ax[0].plot(np.exp(fit6.fittedvalues), label='予測値', color='tomato')
ax[0].set(xlabel='Time', ylabel='発生率', title='患者発生率の推移')
ax[0].legend()
# 残差の自己相関関数のプロット
plot_acf(fit6.resid, lags=20, auto_ylims=True, ax=ax[1],
title=f'ポアソン回帰:残差の自己相関関数')
ax[1].set(xlabel='Lag', ylabel='ACF')
# 修飾
plt.tight_layout()
plt.show()【実行結果】
発生率の予測値のグラフを描画しました。

⑧ 自己回帰AR(6)モデル:介入×時間+季節成分モデル
ラグ6、周期12の自己回帰モデル(ARモデル)で分析してみます。
禁煙介入smokbanを説明変数(外因性変数:exog)で指定します。
### おまけ:AR6+季節成分
from statsmodels.tsa.ar_model import AutoReg
fit_ar6 = AutoReg(endog=data['aces'], lags=6, seasonal=True, period=12,
exog=data['smokban']).fit()
print(fit_ar6.summary())【実行結果】

予測値と誤差の自己相関関数を描画します。
# 描画
fit_plot(fit_ar6.fittedvalues, fit_ar6.resid, 'fit AR(6), period=12')【実行結果】
予測値は、一般化線形モデルよりも観測値に沿っている様子が分かります。

第4章 へ続く
■次回の取り組みテーマ
状態空間モデル:ローカルレベルモデル
・GaussianRandomWalk
・AR:AR(1)
・pymc_experimental.statespace
次の記事
前の記事
目次
ブログの紹介
note で4つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
2.実験!たのしいベイズモデリングをPyMC Ver.5で
書籍「たのしいベイズモデリング」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learn と PyTorch の教科書です。
よかったらぜひ、お試しくださいませ。
4.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Python のコラムを不定期に綴っています。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
最後までお読みいただきまして、ありがとうございました。
