「Pythonによる異常検知」を寄り道写経～第１章1.3節「教師あり学習－分類と回帰」

ネイピア DS

2024年5月15日 11:31

第１章「機械学習と統計解析の基本モデル」

書籍の著者　曽我部東馬先生、監修　曽我部完先生

この記事は、テキスト「Pythonによる異常検知」第１章「機械学習と統計解析の基本モデル」1.3節「教師あり学習－分類と回帰」の通称「寄り道写経」を取り扱います。

今回は機械学習の一分野「教師あり学習」を寄り道写経します！
（注）異常検知はありません。

テキストは「異常検知と機械学習の誤差関数の関係」を重視して、異常検知に入る前に機械学習・統計解析そのものと誤差関数を学びます。
ではテキストを開いて教師あり学習の旅に出発です🚀

はじめに

テキスト「Pythonによる異常検知」のご紹介

このシリーズは書籍「Pythonによる異常検知」（オーム社、「テキスト」と呼びます）の寄り道写経です。

テキストは、2021年2月に発売され、機械学習等の誤差関数から異常検知を解明して、異常検知に関する実践的なPythonコードを提供する素晴らしい書籍です。
とにかく「誤差関数」と「異常度」の強い結びつきを堪能できる１冊です。

引用表記

この記事は、出典に記載の書籍に掲載された文章及びコードを引用し、適宜、掲載文章とコードを改変して書いています。
【出典】
「Pythonによる異常検知」第１版第６刷、著者曽我部東馬、監修者曽我部完、オーム社

記事中のイラストは、「かわいいフリー素材集いらすとや」さんのイラストをお借りしています。
ありがとうございます！

1.3 教師あり学習－分類と回帰

主に Jupyter Notebook 形式（拡張子 .ipynb）でPythonコードを書きます。

今回の寄り道ポイントは次のとおりです。

サポートベクトルマシン
- サポートベクトルマシンのヒンジ誤差関数を scikit-learn ライブラリを用いて実装します。
- TensorFlow V1 を用いたテキストのSVM回帰のコードを TensorFlow V2 で動作するように修正します。
- サポートベクトルマシンの二乗誤差関数・$${\varepsilon-}$$不感誤算関数の比較をテキストにならって実行します。
ランダムフォレスト、AdaBoost、勾配ブースティング決定木、XGブースティング決定木による回帰を scikit-learn などのライブラリを用いて実装します。

この記事で用いるライブラリをインポートします。

### インポート

# 数値計算
import numpy as np 

# 機械学習
from sklearn.svm import LinearSVC, SVC
from sklearn.ensemble import RandomForestRegressor
from sklearn.ensemble import AdaBoostRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import GradientBoostingRegressor
import xgboost as xgb
from sklearn.metrics import (
                    mean_absolute_error, root_mean_squared_error, r2_score)

# 決定境界描画
from sklearn.inspection import DecisionBoundaryDisplay
from matplotlib.colors import ListedColormap

# 描画
import matplotlib.pyplot as plt
plt.rcParams['font.family'] = 'Meiryo'

サポートベクトルマシン（SVM）から旅がはじまります。

SVMによる分類～ヒンジ誤差関数

テキストのオリジナルコード（svm_hinge.py）に代えてscikit-learnで実装します。
異常データの個数変化と分類の境界線変化をシミュレーションします。

最初にデータ作成関数を定義します。

### データ作成関数 ※テキストのコードを引用、一部改変して関数化
def make_data(n_err, seed=88):

    ## 初期値設定
    # 乱数生成器
    rng = np.random.default_rng(seed=seed)

    ## 説明変数Xの作成 shape=(40, 2)
    X = np.zeros((40,2))
    # 1列目
    #   クラス１
    X[0:20, 0] = rng.standard_normal(20) - 25
    #   クラス２
    X[20:, 0] = rng.standard_normal(20) - 5
    #   クラス１に外れ値を生成
    X[0:n_err, 0] = X[0:n_err, 0] + 44
    # 2列目
    X[:, 1] = (rng.integers(low=-30, high=30, size=40))

    # 目的変数y（正解ラベル）の作成（ラベル：1と-1）
    y = np.zeros(40)
    y[0:20] = np.ones(20)
    y[20:] = -np.ones(20)

    return X, y

続いて scikit-learn の LinearSVC による分類＆結果の可視化を関数化します。
LinearSVC の引数 loss でヒンジ誤差関数を指定します。
境界線の描画には scikit-learn の DecisionBoundaryDisplay.from_estimator() を利用しました。

### scikit-learnのLinearSVCで分類して結果を可視化する関数の定義
# テキストのvisualize_svm関数の別コード化

def plot_LinearSVC(n_err):
    # データの作成
    X, y = make_data(n_err)

    # SVCの実行 # 引数penalty='l2'（デフォルト値）
    clf_svc = LinearSVC(loss='hinge', dual='auto', C=0.1, max_iter=10000)
    clf_svc.fit(X, y)

    # 散布図の描画
    # 色の設定
    cmap_bound = ListedColormap(['tab:red', 'tab:blue'])
    # 描画領域の設定
    fig, ax = plt.subplots(figsize=(5, 4))
    # 決定境界の描画
    DecisionBoundaryDisplay.from_estimator(
        clf_svc, X, response_method='predict', cmap=cmap_bound,
        plot_method='contour', xlabel='$x$', ylabel='$y$', alpha=0.3, ax=ax)
    # 観測値の散布図の描画
    plt.scatter(X[:20, 0], X[:20, 1], marker='o', s=100, c='tab:blue',
                ec='white', alpha=0.8)
    plt.scatter(X[20:, 0], X[20:, 1], marker='x',s=80, c='tab:orange')
    # 修飾
    ax.set_title('LinearSVC(ヒンジ損失)による二値分類\n'
                 f'異常データ数: {n_err}')
    plt.show

では、異常データの個数を変えてみて、境界線の変化を楽しみましょう。
テキストの図1.12に対応します。

### 異常値数 4のケース 図1.12に対応
n_err = 4
plot_LinearSVC(n_err)

【実行結果】
青い点と黄色の✕点の分類を試みています。
青赤線が青い点と黄色の点の境界線です。
右側の青い点を異常値と見立てて、個数を変化させていきます。

### 異常値数 7のケース 図1.12に対応
n_err = 7
plot_LinearSVC(n_err)

【実行結果】
境界線が右側に引き寄せられて、ギリギリ黄色の点を識別出来ている状況です。

### 異常値数 9のケース 図1.12に対応
n_err = 9
plot_LinearSVC(n_err)

【実行結果】
境界線が90度回転してしまいました。

### 異常値数 10のケース 図1.12に対応
n_err = 10
plot_LinearSVC(n_err)

【実行結果】
右側の青い点の数が増えた結果、境界線が黄色の点を越えてしまいました。

### 異常値数 11のケース 図1.12に対応
n_err = 11
plot_LinearSVC(n_err)

【実行結果】

非線形の境界を扱える SVC による分類を可視化してみましょう。

### scikit-learnのSVCで分類 kernel='rbf' 図1.12に対応

# データの作成
n_err = 7
X, y = make_data(n_err)

# SVCの実行
clf_svc = SVC(C=0.2, kernel='rbf')
clf_svc.fit(X, y)

# 散布図の描画
# 色の設定
cmap_bound = ListedColormap(['tab:red', 'tab:blue', ])
# 描画領域の設定
fig, ax = plt.subplots(figsize=(5, 4))
# 決定境界の描画
DecisionBoundaryDisplay.from_estimator(
    clf_svc, X, response_method='predict', cmap=cmap_bound, plot_method='contour',
    xlabel='$x$', ylabel='$y$', alpha=0.3, ax=ax)
# 観測値の散布図の描画
plt.scatter(X[:20, 0], X[:20, 1], marker='o', s=100, c='tab:blue',
            ec='white', alpha=0.8)
plt.scatter(X[20:, 0], X[20:, 1], marker='x',s=80, c='tab:orange')
# 修飾
ax.set_title(f'scikit-learn SVCによる二値分類\n異常データ数: {n_err}');

【実行結果】
楕円の境界線が爆誕！
内側に黄色の点を囲い込み、外側に青い点を位置づける境界です。

SVM回帰

テキストのオリジナルコード「svr.py」のエラー解消を試みます。
オリジナルコードに含まれる TensorFlow がバージョン１であり、現在のバージョン２で実行するとエラーが発生します。
雑な対応ですが、コードを変更して動かしてみましょう。

以下のコードはテキストのオリジナルコードを引用して、★印の箇所を変更しました。
「★V2対応」がTensorFlowバージョン２対応のための変更です。
「★other」は使い勝手を良くするための変更です。

### SVRクラスの定義
# V1→V2対応の参考情報: https://qiita.com/rawHam/items/626d9b119cbefcee1452
# eager_execution : https://stackoverflow.com/questions/53429896/how-do-i-disable-tensorflows-eager-execution

import numpy as np
from matplotlib import pyplot as plt
import tensorflow as tf
tf.compat.v1.disable_eager_execution() # ★V2対応：追加

class SVR(object):
    
    # ★other：引数に誤差関数の種類 loss_func を追加
    def __init__(self, epsilon=0.5, loss_func=0):
        self.epsilon = epsilon
        # ★other：引数に誤差関数の種類 loss_func を追加したことに伴うコード追加
        self.loss_func = loss_func

    def fit(self, X, y, epochs=100, learning_rate=0.1):
        self.sess = tf.compat.v1.Session()

        feature_len = X.shape[-1] if len(X.shape) > 1 else 1
        if len(X.shape) == 1:
            X = X.reshape(-1, 1)
        if len(y.shape) == 1:
            y = y.reshape(-1, 1)
        
        # ★V2対応：次の２行を下の２行に差し替える
        # self.X = tf.placeholder(dtype=tf.float32, shape=(None, feature_len))
        # self.y = tf.placeholder(dtype=tf.float32, shape=(None, 1))
        self.X = tf.compat.v1.placeholder(dtype=tf.float32, 
                                          shape=(None, feature_len))
        self.y = tf.compat.v1.placeholder(dtype=tf.float32, shape=(None, 1))

        # ★V2対応：tf.random_normal を tf.random.normal に変更
        self.W = tf.Variable(tf.random.normal(shape=(feature_len, 1)))
        self.b = tf.Variable(tf.random.normal(shape=(1,)))

        self.y_pred = tf.matmul(self.X, self.W) + self.b
        
        # ★other：誤差関数の選択 loss_func=0: ε-不感誤差関数、1: 二乗誤差関数
        if self.loss_func == 0:
            self.loss = (
                tf.norm(self.W)/2
                + tf.reduce_mean(tf.maximum(0., tf.abs(self.y_pred - self.y)
                                            - self.epsilon)))
        else:
            self.loss = tf.reduce_mean(tf.square(self.y - self.y_pred))
        
        # ★V2対応：次の行をその下の行に差し替える
        # opt = tf.train.GradientDescentOptimizer(learning_rate=learning_rate)
        opt = tf.compat.v1.train.GradientDescentOptimizer(
                                                learning_rate=learning_rate)
        
        opt_op = opt.minimize(self.loss)

        # ★V2対応：次の行をその下の行に差し替える
        # self.sess.run(tf.global_variables_initializer())
        self.sess.run(tf.compat.v1.global_variables_initializer())

        # ★other：損失値の履歴を格納するリストの初期化
        self.loss_history = []

        for i in range(epochs):
            loss = self.sess.run(
                self.loss,
                {
                    self.X: X,
                    self.y: y
                }
            )
            
            # ★other：損失値をリストに格納
            self.loss_history.append([i + 1, loss])

            print("{}/{}: loss: {}".format(i + 1, epochs, loss))

            self.sess.run(
                opt_op,
                {
                    self.X: X,
                    self.y: y
                }
            )
        
        # ★other：損失値の履歴をnumpy配列化
        self.loss_history = np.array(self.loss_history)
        
        return self

    def predict(self, X, y=None):
        if len(X.shape) == 1:
            X = X.reshape(-1, 1)

        y_pred = self.sess.run(
            self.y_pred,
            {
                self.X: X
            }
        )
        return y_pred

続いてデータを作成します。
テキストのコードを引用し、設定内容等を改変しています。

### データの作成　※テキストのコードを引用、一部改変

## 設定
# 傾きと切片
slope = -1
intercept = 2
# 乱数シード
seed = 10

## データの作成
# 乱数生成器の設定
rng = np.random.default_rng(seed=seed)
# x軸の値の設定 shape=(20,)
x = np.linspace(start=0, stop=5, num=20)
# yの値の作成：回帰式＋標準正規分布乱数 shape=(20,)
y = slope * x + intercept + rng.standard_normal(size=(len(x),))

## 描画
fig, ax = plt.subplots(figsize=(6, 4))
ax.plot(x, y, 'o', ms=10, color='wheat', mec='tab:orange')
ax.set(xlabel='$x$', ylabel='$y$', title='作成データの散布図')
plt.grid(lw=0.5);

【実行結果】
右肩下がりの傾向があるデータになりました。

それでは、テキストオリジナルコード svr.py に含まれる SVR クラスを用いて、回帰タスクを実行します。
まずは ε-不感誤差関数のSVRで予測を実行します。

### ε-不感誤差関数のSVRの実行 ※実行ごとに値が変わります

# SVRインスタンスの生成 ※テキストのSVRクラスを利用
clf_epsilon = SVR(epsilon=0.2, loss_func=0) # loss_func=0 ε-不感誤差関数
# SVRの学習
clf_epsilon.fit(x, y, epochs=100, learning_rate=0.1)
# 学習データによる目的変数の予測
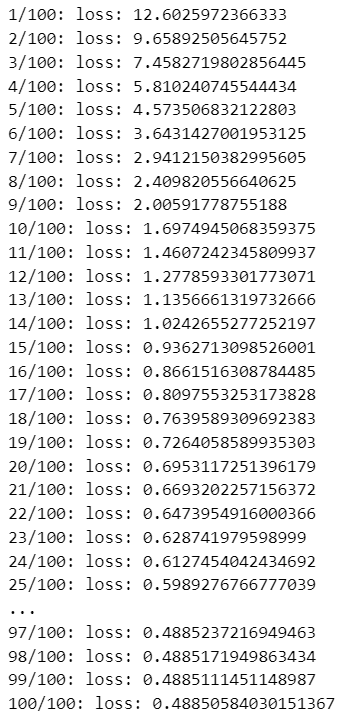
y_pred = clf_epsilon.predict(x)

【実行結果】
各エポックの損失値が表示されます。

続いて 2乗誤差関数のSVRで予測を実行します。

### 2乗誤差関数のSVRの実行 ※実行ごとに値が変わります

# SVRインスタンスの生成 ※テキストのSVRクラスを利用
clf_square = SVR(epsilon=0.2, loss_func=1) # loss_func=1 2乗誤差関数
# SVRの学習
clf_square.fit(x, y, epochs=100, learning_rate=0.1)
# 学習データによる目的変数の予測
y_pred2 = clf_square.predict(x)

【実行結果】

２つの誤差関数による予測値を可視化しましょう。
テキストの図1.16左に対応します。

### 予測値の描画 図1.16左

# 描画領域の設定
fig, ax = plt.subplots(figsize=(6, 4))
# 実際値の散布図の描画
ax.plot(x, y, 'o', ms=10, color='wheat', mec='tab:orange', label='実際値')
# ε-不感誤差関数による予測値の描画
ax.plot(x, y_pred, '-', color='tab:blue',
        label=r'予測値: $\varepsilon$-不感誤差関数')
# 2乗誤差関数による予測値の描画
ax.plot(x, y_pred2, '--', color='tab:red', label='予測値: 2乗誤差関数')
# 修飾
ax.set(xlabel='$x$', ylabel='$y$', title='実際値と予測値のプロット')
ax.grid(lw=0.5)
ax.legend();

【実行結果】
２つの誤差関数の予測値は微妙に異なるようです。

学習曲線（損失値）を可視化しましょう。
テキストの図1.16右に対応します。

### 学習曲線の描画 図1.16右 ★テキストに無いコード

# 描画領域の設定
fig, ax = plt.subplots(figsize=(5, 4))
# ε-不感誤差関数の学習曲線（損失値）の描画
ax.plot(clf_epsilon.loss_history[:, 0], clf_epsilon.loss_history[:, 1],
        color='tab:blue', label=r'$\varepsilon$-不感誤差関数')
# 2乗誤差関数の学習曲線（損失値）の描画
ax.plot(clf_square.loss_history[:, 0], clf_square.loss_history[:, 1],
        color='tab:red', ls='--', label='2乗誤差関数')
# 修飾
ax.set(xlabel='Epoch', ylabel='Loss', xlim=(0, 100), title='学習曲線')
plt.grid(lw=0.5)
plt.legend();

【実行結果】
テキストは「誤差関数収束値が高いほうが汎化機能として捉えることができるので、ε-不感誤差関数のほうが高い汎化機能を持つことが期待できます」としています。

ランダムフォレスト回帰

ここからは決定木系の４つの回帰アルゴリズムで予測を行います。
パラメータ値を適宜変えてみて、予測値の変化を楽しんでくださいね！

データを作成します。
テキストのデータを引用いたします。

### データの作成 ★テキストのデータを引用
inputs = np.array([5.0, 7.0, 12.0, 20.0, 23.0, 25.0,
                    28.0, 29.0, 34.0, 35.0, 40.0])
target = np.array([62.0, 60.0, 83.0, 120.0, 158.0, 172.0,
                    167.0, 204.0, 189.0, 140.0, 166.0])

最初はランダムフォレストから。
テキストのオリジナルコード（randomforest.py）に代えてscikit-learnで実装します。
パラメータはなるべくテキストの設定値に合わせています。

### scikit-learnのRandomforest

# パラメータの設定
n_estimators = 3       # 決定木の数
max_depth = 2          # 木の深さ
min_samples_split = 5  # 分割時のサンプル数最小値
seed = 1234            # 乱数シード

## ランダムフォレスト回帰器による学習と予測の実行
# ランダムフォレスト回帰器の設定
rfr = RandomForestRegressor(
    n_estimators=n_estimators, max_depth=max_depth,
    min_samples_split=min_samples_split, max_features=1, random_state=seed)
# 学習と予測
rfr.fit(inputs.reshape(-1, 1), target)
y_pred_rfr = rfr.predict(inputs.reshape(-1, 1))
print('予測値:')
print(y_pred_rfr)

## 評価指標の算出 MAE, RMSE, R²
mae = mean_absolute_error(y_true=target, y_pred=y_pred_rfr)
rmse = root_mean_squared_error(y_true=target, y_pred=y_pred_rfr)
r2 = r2_score(y_true=target, y_pred=y_pred_rfr)
print(f'\nRMSE: {rmse:6.3f}')
print(f'MAE : {mae:6.3f}')
print(f'R²  : {r2:6.3f}')

## 実際値の散布図と予測値の折れ線グラフの描画
fig, ax = plt.subplots(figsize=(6, 4))
ax.plot(inputs, target, 'o', ms=10, color='wheat', mec='tab:orange',
        label='実際値')
ax.step(inputs, y_pred_rfr, color='tab:blue', label='予測値')
ax.set(xlabel='$Input$', ylabel='$Target$', ylim=(50, 220),
       title='scikit-learnのランダムフォレスト回帰による予測')
plt.legend(loc='lower right')
plt.grid(lw=0.5)
plt.show()

【実行結果】
Step状（階段状）のカクカクとした予測ができました。

AdaBoost回帰

同一データをAdaBoost回帰で予測します。
テキストのオリジナルコード（adaboost.py）に代えてscikit-learnで実装します。
推定器に決定木（DecisionTreeRegressor）を用いています。

### scikit-learnのAdaBoost

# パラメータの設定
n_estimators = 10    # 決定木の数
max_depth = 4        # 決定木の木の深さ
learning_rate = 1    # 学習率 0.2で誤差０になる
seed = 1234          # 乱数シード

## AdaBoost回帰による学習と予測の実行
# AdaBoost回帰器の設定 ※なるべくテキストのパラメータ値と同値を使用
adr = AdaBoostRegressor(
    estimator=DecisionTreeRegressor(max_depth=max_depth),
    n_estimators=n_estimators, learning_rate=learning_rate, random_state=seed,
    loss='linear',          # default:'linear', 'square', 'exponential'
    )
# 学習と予測
adr.fit(inputs.reshape(-1, 1), target)
y_pred_adr = adr.predict(inputs.reshape(-1, 1))
print('予測値:')
print(y_pred_adr)

## 評価指標の算出 MAE, RMSE, R²
mae = mean_absolute_error(y_true=target, y_pred=y_pred_adr)
rmse = root_mean_squared_error(y_true=target, y_pred=y_pred_adr)
r2 = r2_score(y_true=target, y_pred=y_pred_adr)
print(f'\nRMSE: {rmse:6.3f}')
print(f'MAE : {mae:6.3f}')
print(f'R²  : {r2:6.3f}')

## 実際値の散布図と予測値の折れ線グラフの描画
fig, ax = plt.subplots(figsize=(6, 4))
ax.plot(inputs, target, 'o', ms=10, color='wheat', mec='tab:orange',
        label='実際値')
ax.step(inputs, y_pred_adr, color='tab:blue', label='予測値')
ax.set(xlabel='$Input$', ylabel='$Target$', ylim=(50, 220),
       title='scikit-learnのAdaBoost回帰による予測')
plt.legend(loc='lower right')
plt.grid(lw=0.5)
plt.show()

【実行結果】
予測値が実際値とほぼピッタリ一致しています。
過学習状態ですね・・・

勾配ブースティング回帰

同一データを勾配ブースティング回帰で予測します。
テキストのオリジナルコード（gradientboost.py）に代えてscikit-learnで実装します。

### scikit-learnの勾配ブースティング回帰

# パラメータの設定
n_estimators = 5     # 決定木の数
max_depth = 2        # 決定木の木の深さ
learning_rate = 0.5  # 学習率 1.02 でR²=0.999
seed = 1234          # 乱数シード

## 勾配ブースティング回帰による学習と予測の実行
# 勾配ブースティング回帰器の設定 ※なるべくテキストのパラメータ値と同値を使用
gbr = GradientBoostingRegressor(
    n_estimators=n_estimators, max_depth=max_depth, learning_rate=learning_rate,
    random_state=seed,
    loss='squared_error',   # default: 'squared_error', 'absolute_error', ...
    )
# 学習と予測
gbr.fit(inputs.reshape(-1, 1), target)
y_pred_gbr = gbr.predict(inputs.reshape(-1, 1))
print('予測値:')
print(y_pred_gbr)

## 評価指標の算出 MAE, RMSE, R²
mae = mean_absolute_error(y_true=target, y_pred=y_pred_gbr)
rmse = root_mean_squared_error(y_true=target, y_pred=y_pred_gbr)
r2 = r2_score(y_true=target, y_pred=y_pred_gbr)
print(f'\nRMSE: {rmse:6.3f}')
print(f'MAE : {mae:6.3f}')
print(f'R²  : {r2:6.3f}')

## 実際値の散布図と予測値の折れ線グラフの描画
fig, ax = plt.subplots(figsize=(6, 4))
ax.plot(inputs, target, 'o', ms=10, color='wheat', mec='tab:orange',
        label='実際値')
ax.step(inputs, y_pred_gbr, color='tab:blue', label='予測値')
ax.set(xlabel='$Input$', ylabel='$Target$', ylim=(50, 220),
       title='scikit-learnの勾配ブースティング回帰による予測')
plt.legend(loc='lower right')
plt.grid(lw=0.5)
plt.show()

【実行結果】
こちらは何だかいい感じの予測値に見えます！

XGブースティング回帰

同一データをXGブースティング回帰で予測します。
テキストのオリジナルコード（xgboost.py）に代えてxgboostライブラリで実装します。
パラメータ値はテキストの設定から変えています。

### XGBoost回帰 w/ Scikit-Learn API

# パラメータの設定
n_estimators = 3     # 決定木の数       テキストは5
max_depth = 2        # 決定木の木の深さ テキストは3
_lambda = 0          # λ               テキストは0
gamma = 0            # γ               テキストは0
learning_rate = 1.2  # 学習率
seed = 1234          # 乱数シード

## XGBoost回帰器による学習と予測の実行
# XGBoost回帰器の設定
xgr = xgb.XGBRegressor(
    n_estimators=n_estimators, max_depth=max_depth, reg_lambda=_lambda,
    gamma=gamma, learning_rate=learning_rate, objective='reg:squarederror',
    random_state=seed)
# 学習と予測
xgr.fit(inputs.reshape(-1, 1), target)
y_pred_xgr = xgr.predict(inputs.reshape(-1, 1))
print('予測値:')
print(y_pred_xgr)

## 評価指標の算出 MAE, RMSE, R²
mae = mean_absolute_error(y_true=target, y_pred=y_pred_xgr)
rmse = root_mean_squared_error(y_true=target, y_pred=y_pred_xgr)
r2 = r2_score(y_true=target, y_pred=y_pred_xgr)
print(f'\nRMSE: {rmse:6.3f}')
print(f'MAE : {mae:6.3f}')
print(f'R²  : {r2:6.3f}')

## 実際値の散布図と予測値の折れ線グラフの描画
fig, ax = plt.subplots(figsize=(6, 4))
ax.plot(inputs, target, 'o', ms=10, color='wheat', mec='tab:orange',
        label='実際値')
ax.step(inputs, y_pred_xgr, color='tab:blue', label='予測値')
ax.set(xlabel='$Input$', ylabel='$Target$', ylim=(50, 220),
       title='XGBoost回帰による予測')
plt.legend(loc='lower right')
plt.grid(lw=0.5)
plt.show()

【実行結果】
微妙に過学習気味！？

今回の寄り道写経は以上です。

シリーズの記事

次の記事

前の記事

ブログの紹介

note で７つのシリーズ記事を書いています。
ぜひ覗いていってくださいね！

１．のんびり統計

統計検定２級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定２級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。

２．実験！たのしいベイズモデリング１＆２をPyMC Ver.5で

書籍「たのしいベイズモデリング」・「たのしいベイズモデリング２」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルはＲ言語＋Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう！

３．実験！岩波データサイエンス1のベイズモデリングをPyMC Ver.5で

書籍「実験！岩波データサイエンスvol.1」の４人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう！

４．楽しい写経ベイズ・Python等

ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀

５．RとStanではじめる心理学のための時系列分析入門を PythonとPyMC Ver.5 で

書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん！
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。

６．データサイエンスっぽいことを綴る

統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。

７．Python機械学習プログラミング実践記

書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。

最後までお読みいただきまして、ありがとうございました。

いいなと思ったら応援しよう！

この記事が参加している募集

#新生活をたのしく

47,053件

「Pythonによる異常検知」を寄り道写経 ～ 第１章1.3節「教師あり学習－分類と回帰」

第１章「機械学習と統計解析の基本モデル」

はじめに

テキスト「Pythonによる異常検知」のご紹介

引用表記

1.3 教師あり学習－分類と回帰

SVMによる分類～ヒンジ誤差関数

SVM回帰

ランダムフォレスト回帰

AdaBoost回帰

勾配ブースティング回帰

XGブースティング回帰

シリーズの記事

ブログの紹介

いいなと思ったら応援しよう！

この記事が参加している募集

「Pythonによる異常検知」を寄り道写経～第１章1.3節「教師あり学習－分類と回帰」