
8-3 母平均の片側t検定 ~ t分布・t値・p値
今回の統計トピック
統計的仮説検定のトピック「1標本の母平均の$${t}$$検定」を深掘りします。
スチューデントの$${t}$$検定を手計算、EXCEL、Pythonで実践いたします。
公式問題集の準備
「公式問題集」の問題を利用します。お手元に公式問題集をご用意ください。
公式問題集が無い場合もご安心ください!
「知る」「実践する」の章で、のんびり統計をお楽しみください!
問題を解いて、知る・実践する
今回の記事の構成
この記事は、通常の記事構成と違う章立てにいたします。
「問題を解く」「知る」「実践する」を1つの章にまとめます。
1標本の母平均の$${t}$$検定の一連の流れを、手作業・EXCEL・Pythonで実践いたします。

📘公式問題集のカテゴリ
検定の分野
問3 母平均の片側$${t}$$検定(株価の月次変化率)
試験実施年月
統計検定2級 2019年6月 問15(回答番号27)
📕公式テキスト:4.3.2 正規分布の母平均に関する検定(母分散が未知の場合、$t$検定)(144ページ~)
問題
公式問題集をご参照ください。
解き方
題意
与えられた条件から検定統計量を求めて、1標本の母平均の検定を行います。
【条件】
・標本は互いに独立に正規分布$${N(\mu, \sigma^2)}$$に従う。
・標本サイズ:$${24}$$
・標本平均:$${3.23}$$
・不偏分散:$${8.72^2}$$
・帰無仮説:母平均$${\mu=0}$$
・対立仮説:母平均$${\mu>0}$$
読み解き
条件から統計的仮説検定の主題を読み解きます。
帰無仮説「母平均=0」より、「1標本の母平均の検定」です。
標本が正規分布に従うこと、母分散が未知であること、不偏分散を用いることより、「検定統計量$${t}$$と$${t}$$分布」を利用します
対立仮説「母平均>0」の不等号の向きより、「片側検定」で「上側確率」を利用します。
この問題の統計的仮説検定の概要を図示します。
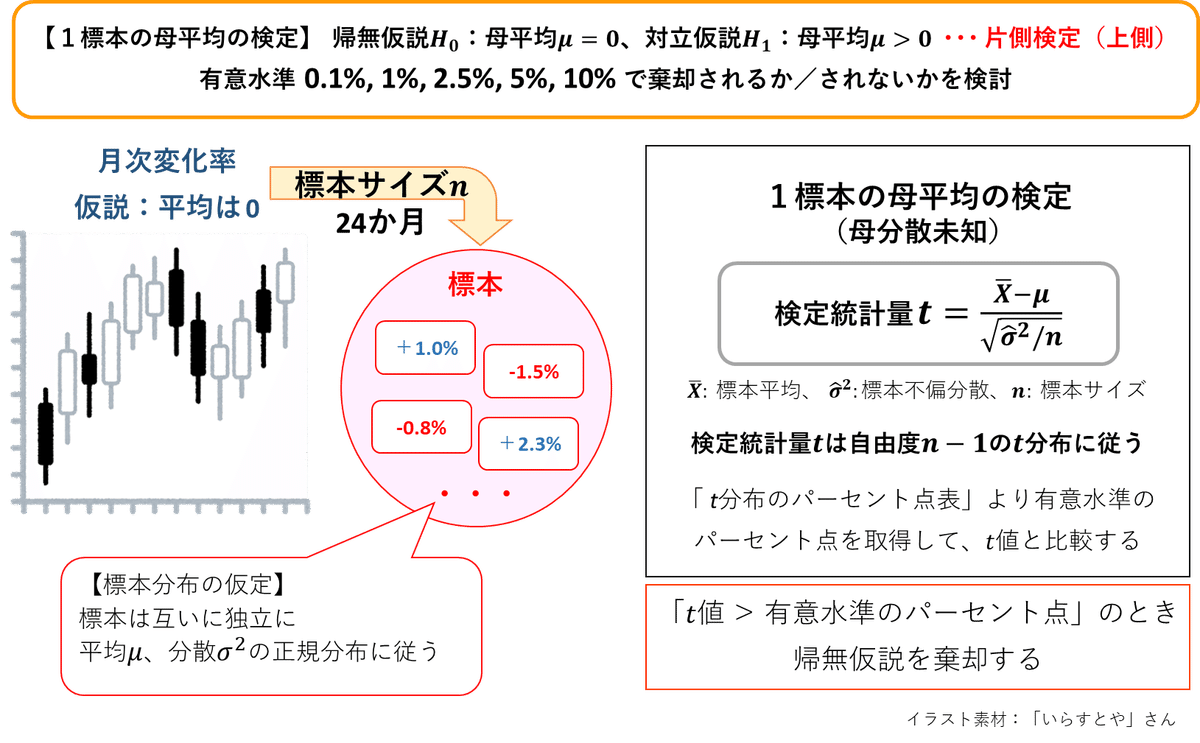
統計的仮説検定の手段
今回は、①手計算、②EXCEL、③Python の3つの手段で検定を実施いたします。
手計算で検定
ステップ1:検定統計量$${t}$$を計算する
帰無仮説が正しいと仮定するときの検定統計量 $${t}$$ を計算します。
計算結果の値を「$${t}$$値」と呼びます。
この問題で「帰無仮説が正しいと仮定する」とは、「母平均$${\mu=0}$$である」と仮定することです。
検定統計量$${t}$$の計算式は次のとおりです。
■公式
検定統計量$${t=\cfrac{\bar{X}-\mu}{\sqrt{\hat{\sigma}^2/n}}}$$
ただし、$${\bar{X}}$$:標本平均、$${\mu}$$:帰無仮説の母平均、$${\hat{\sigma}^2}$$:標本不偏分散、$${n}$$:標本サイズ
問題文で与えられた$${\bar{X}=3.23}$$、$${\mu=0}$$、$${\hat{\sigma}^2=8.72^2}$$、$${n=24}$$を用いて検定統計量$${t}$$を計算します。
$$
\begin{align*}
t&=\cfrac{\bar{X}-\mu}{\sqrt{\hat{\sigma}^2/n}} \\
\\
&=\cfrac{3.23-0}{\sqrt{8.72^2/24}} \\
\\
&=\cfrac{3.23}{8.72/\sqrt{24}} \\
\\
&= 1.8146 \cdots (電卓で計算)
\end{align*}
$$
$${t}$$値は$${1.815}$$です。

ステップ2:有意水準に対応する$${\boldsymbol{t}}$$分布のパーセント点の取得
問題で与えられた5つの有意水準のうち、$${t}$$分布のパーセント点表で取得可能な4つの有意水準について、上側確率のパーセント点を取得します。
片側検定ですので、有意水準を2で割る必要は無く(両側検定のように)、有意水準の値そのままでOKです。
自由度は「標本サイズ-1」ですので、$${23}$$です。
では、$${t}$$分布のパーセント点表を見ましょう。
黄色の横並びの有意水準、自由度$${23}$$の交差点を見ます(赤枠で囲んでいます)。

表より、有意水準に対応する上側確率のパーセント点を取得できました。
$$
\begin{array}{cc:c}
有意水準 & & パーセント点 \\
\hline
1\% & (0.010) & 2.500 \\
2.5\% & (0.025) & 2.069 \\
5\% & (0.050) & 1.714 \\
10\% & (0.100) & 1.319 \\
\end{array}
$$

ステップ3:$${\boldsymbol{t}}$$値と有意水準のパーセント点を比較する
「$${t}$$値 > 有意水準のパーセント点」のとき、帰無仮説を棄却します。
では、4つの有意水準で検定を進めて行きましょう!
・有意水準1%のとき、$${t=1.815 < 2.500}$$となり、棄却されません。
・有意水準2.5%のとき、$${t=1.815 < 2.069}$$となり、棄却されません。
・有意水準5%のとき、$${t=1.815 > 1.714}$$となり、棄却されます。
・有意水準10%のとき、$${t=1.815 > 1.319}$$となり、棄却されます。
有意水準 5% のとき、帰無仮説は棄却されます。
そして、有意水準 2.5% のとき、帰無仮説は棄却されません。
最終ステップ:解答
解答は「有意水準 5% で棄却できます。しかし、有意水準 2.5% では棄却できません」となります。
1標本の母平均の$${\boldsymbol{t}}$$検定の可視化
$${t}$$分布の確率密度関数のグラフで、有意水準と$${t}$$値の関係を確認しましょう。
$${t}$$値の赤い線は、上側 5% 点(黒い点線)より上側にあり、上側 2.5% 点(緑の点線)より下側にあることが分かります。
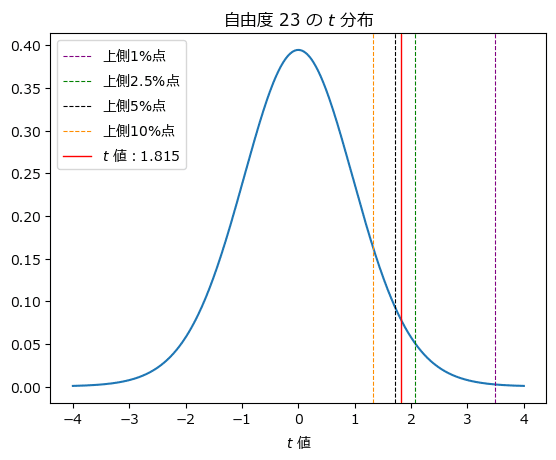
手計算は以上となります。

データの作成
出題の標本データを擬似的に再現
これからEXCELとPythonで$${t}$$検定を行うに当たって、どうしても標本データを使いたくなりました。
そこで、出題条件(基本統計量)を満たす標本データを疑似的に作成しました。
あくまで疑似データですので、問題集の基礎にある標本データとの一致性を確保していません。
予めお断りいたします。
EXCELとPythonでは、この疑似標本データを用いて、$${t}$$検定を行います。

データの一覧(カンマ区切り)
疑似データの内容です。
23.37900286, 10.28382166, 0.422245555, 1.877701587, 11.73994475, -7.033758489, -2.007622731, -1.760822802, 6.272246216, 14.97467646, 4.82210334, 10.75385788, 4.082626014, 12.7291657, -1.423259178, -3.017557325, 8.981095445, 7.569948543, -6.551730313, -3.115627609, -7.918731387, -4.004708233, -13.61856747, 10.08394954
CSVファイルのダウンロード
こちらのリンクからCSVファイルをダウンロードできます。
EXCELとPythonのコード例では別途データを用意しているので、こちらからデータを取得する必要はありません。
データ作成に使用したツールの紹介
データ作成にはフリーの統計分析ソフト「HAD」を利用しました。
ありがとうございます!
EXCELで検定
EXCELで1標本の母平均の$${t}$$検定を行います。
記事「8-1 母平均の検定の考え方」で紹介した計算シートをリサイクル活用いたします!
計算シートの全体像
左側のデータ枠に「疑似標本データ」を設定しています。
時系列推移グラフとヒストグラムでデータの外観を確認しましょう。

統計的仮説検定の実行
次の条件を入力パラメータに設定して、$${t}$$値、$${p}$$値を自動計算します。
・帰無仮説の平均: 0
・有意水準: 0.1%、1%、2.5%、5%、10%を指定
・検定方法: 片側検定(上側)
有意水準 5% の例です。

$${p}$$値は$${t}$$値から計算した確率値です。
$${p}$$値が有意水準の値よりも小さいとき、帰無仮説を棄却します。
今回の$${p}$$値は$${0.0413}$$($${4.13\%}$$)です。
有意水準 5% のとき、$${p}$$値は$${0.0413}$$は有意水準の値よりも小さいので、帰無仮説は棄却されます。
有意水準 2.5% のとき、$${p}$$値は$${0.0413}$$は有意水準の値よりも大きいので、帰無仮説は棄却されません。
よって、解答は「有意水準 5% で棄却できます。しかし、有意水準 2.5% では棄却できません」となります。
EXCEL計算式の補足説明
標本不偏分散は「VAR.S関数」で計算しています。
引数は「標本不偏分散を算定するデータの範囲」です。

$${t}$$値は専用の関数が無いため、検定統計量$${t}$$の計算式を設定しました。

$${t}$$値の上側確率は「T.DIST.RT関数」で計算しています。
この関数は$${t}$$分布の上側確率を算出する関数です。
引数は、$${t}$$値(上側確率パーセント点)と自由度です。
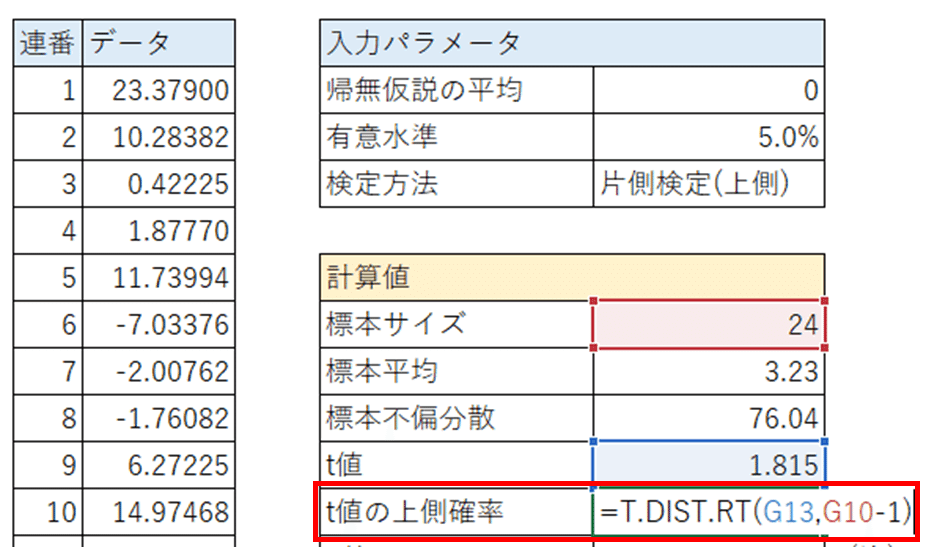
EXCELは以上となります。
EXCELサンプルファイルのダウンロード
こちらのリンクからEXCELサンプルファイルをダウンロードできます。
Pythonで検定
Pythonで1標本の母平均の$${t}$$検定を行います。
SciPy.stats の ttest_1samp で実施できます。
今回は、手組みのコードとttest_1sampを利用したコードの2パターンに取り組みます。
インポート
# 数値計算・統計計算
import numpy as np
from scipy import stats
# 可視化
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'標本データの読み込み
標本サイズ24の疑似標本データ(月次変化率を想定)を読み込みます。
コメントアウトしている最後の2行は、データのCSVファイル出力、CSVファイルの読み込みのコードです。
# 標本データの読み込み
data = np.array([
23.37900286, 10.28382166, 0.422245555, 1.877701587,
11.73994475, -7.033758489, -2.007622731, -1.760822802,
6.272246216, 14.97467646, 4.82210334, 10.75385788,
4.082626014, 12.7291657, -1.423259178, -3.017557325,
8.981095445, 7.569948543, -6.551730313, -3.115627609,
-7.918731387, -4.004708233, -13.61856747, 10.08394954
])
# np.savetxt(r'sample_data.csv', data, delimiter=',', encoding='utf_8_sig')
# data = np.loadtxt(r'sample_data.csv', delimiter=',', encoding='utf_8_sig')標本データの概要の確認
標本サイズ、標本平均、不偏分散を確認します。
問題集の条件と一致しています。
# 標本サイズn、標本平均X_bar、不偏分散sigma2_hatの算出
n = data.shape[0]
X_bar = data.mean()
sigma2_hat = data.var(ddof=1)
print(f'標本サイズ: {n}')
print(f'標本平均: {X_bar:.3f}')
print(f'不偏分散: {np.sqrt(sigma2_hat):.3f}^2')
時系列推移グラフの描画
疑似標本データは24か月の月次データです。
時系列の折れ線グラフでデータの外観を確認しましょう。
# 時系列推移グラフの描画
plt.plot(np.arange(1, n+1), data)
plt.title('株価の月次変化率')
plt.xlabel('月')
plt.ylabel('変化率(%)')
plt.axhline(X_bar, lw=0.5, color='red', label='標本平均')
plt.legend()
plt.show()
-15% から 25% の間をジグザグに変動している様子が分かります。
ヒストグラムの描画
問題集では標本データが正規分布に従う仮定を置いていました。
疑似標本データはどうでしょう?
ヒストグラムで分布の形状を見てみましょう。
seaborn の histplot を利用します。
引数 kde=True を指定して、カーネル密度関数(曲線)を表示します。
# ヒストグラムの描画
sns.histplot(data, bins=10, kde=True)
plt.title('株価の月次変化率のヒストグラム')
plt.xlabel('月次変化率(%)')
plt.show()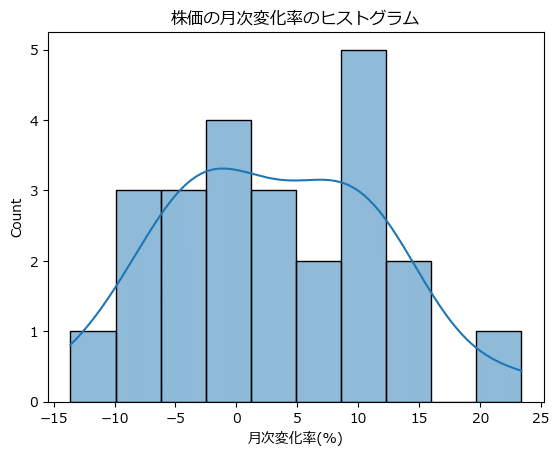
峰が平らのような、微妙に2峰あるような、微妙な形状です。
ひとまず、Shapiro-Wilk検定で正規分布の検定をしておきます。
Shapiro-Wilk検定
帰無仮説「データは正規分布に従う」が棄却されない場合、正規分布に従うと想定します。
stats.shapiro(data)
$${p}$$値(pvalue)は0.89であり、かなり大きな値です。
帰無仮説は棄却されず、疑似標本データは正規分布に従っているものとして取り扱いましょう。

$${\boldsymbol{t}}$$検定の実行
いよいよ$${t}$$検定を実行します!
はじめに、検定統計量$${t}$$を公式どおりに計算するパターンです。
片側検定(上側)のためのコードです。
# 母平均のt検定 片側検定(上側)
# 帰無仮説 H0:μ=0、対立仮説 H1: μ>0
# 設定
mu = 0 # 帰無仮説の母平均
# t値の算出
t_value1 = (X_bar - mu) / np.sqrt(sigma2_hat / n)
# p値の算出 片側検定(上側)
p_value1 = 1 - stats.t.cdf(t_value1, df=n-1)
print(f' t値: {t_value1:.3f}, p値: {p_value1:.3f}({p_value1:.1%})')
# 有意水準のリスト化
alpha_list = [0.001, 0.01, 0.025, 0.05, 0.1]
alpha_list.sort()
# 有意水準のt分布パーセント点(上側)とt値を比較
print('\n有意水準 %点 判定')
print('-------- ----- ------------')
for alpha in alpha_list:
reject = '棄却されない'
t_ppf_alpha = stats.t.ppf(1-alpha, df=n-1)
if t_value1 > t_ppf_alpha: reject = '棄却される'
print(f' {alpha:5.1%} {t_ppf_alpha:.3f} {reject}')
$${t}$$値、$${p}$$値、帰無仮説の棄却判定が出力されました。
解答は「有意水準 5% で棄却できます。しかし、有意水準 2.5% では棄却できません」となります。
■コードの補足
「$${t}$$値の算出」
公式どおりに$${t}$$値を計算しています。
「$${p}$$値の算出」
自由度$${23}$$の$${t}$$分布から、$${t}$$値の上側確率を算出します。
stats.t.cdfで$${t}$$値の累積分布関数の値(=下側確率)を取得して、1から引いて上側確率を求めています。
「有意水準のt分布パーセント点(上側)とt値を比較」
「片側検定(上側)」に即して、有意水準 0.1%、1%、2.5%、5%、10% と$${p}$$値を比較して、棄却する/しないを判定してます。
$${t}$$値と比較する目的で、stats.t.ppf を利用して、各有意水準に関する自由度$${23}$$の$${t}$$分布の上側パーセント点を取得しています。
SciPy の ttest_1samp を利用
ttest_1sampで1標本の母平均の$${t}$$検定を「片側検定(上側)」で実施して、$${t}$$値と$${p}$$値を得ます。
引数は、ttest_1samp(標本データ, popmean=帰無仮説の母平均, alternative=片側検定(上側))です。
# 母平均のt検定 片側検定(上側)
# 設定
mu = 0 # 帰無仮説の母平均
# 1標本のt検定 対立仮説alternative: μ>popmean
t_value2, p_value2 = stats.ttest_1samp(data, popmean=mu, alternative='greater')
print(f't値: {t_value2:.3f}, p値: {p_value2:.3f}({p_value2:.1%})')
$${t}$$値、$${p}$$値が出力されました。
有意水準 5%:$${\alpha=0.05>\text{p\ value}=0.041}$$のとき帰無仮説は棄却されます。
有意水準 2.5%:$${\alpha=0.025<\text{p\ value}=0.041}$$のとき帰無仮説は棄却されません。
解答は「有意水準 5% で棄却できます。しかし、有意水準 2.5% では棄却できません」となります。
■ttest_1sampの補足
alternativeは対立仮説の不等号によって指定値を決定します。
・帰無仮説:母平均≠0 alternative='two-sided' (デフォルト値)
・帰無仮説:母平均>0 alternative='greater'
・帰無仮説:母平均<0 alternative='less'
以上で終了です。
お疲れ様でした。

解答
③ です。
難易度 やさしい
・知識:1標本の母平均の$${t}$$検定、$${t}$$分布のパーセント点表
・計算力:数式組み立て(低)、電卓(低)
・時間目安:1分
おわりに
8章「検定の分野」の3番目の記事ではじめて、①検定統計量を計算して、②検定統計量が従う確率分布を参照して、③帰無仮説を棄却できるかどうかを判断する、という一連の流れを体感できる「統計的仮説検定らしい問題」に取り組みました。
1標本の母平均の$${t}$$検定のツールの対応状況は、Pythonには用意されていますが、EXCELには用意されていないようです。
EXCELには用意されているメジャーな統計的仮説検定を解いてみたいですね。
最後までお読みいただきまして、ありがとうございました。
のんびり統計シリーズの記事
次の記事
前の記事
目次
この記事が気に入ったらサポートをしてみませんか?
