
第19章「単一事例データへのマルチレベルモデルの適用」のベイズモデリングをPyMC Ver.5 で
この記事は、テキスト「たのしいベイズモデリング2」の第19章「単一データへのマルチレベルモデルの適用」のベイズモデルを用いて、PyMC Ver.5で「実験的」に実装する様子を描いた統計ドキュメンタリーです。
最終回の今回も、心理学術的な色合いの濃いベイズ分析です。
この章では、単一事例実験データにマルチレベルモデルを適用して、階層ベイズで分析します、って何書いてるんだろう???
テキストをにらめっこして統計分野の専門用語のイメージをすくい取りつつ、ベイズモデリングに繋げていきたいです。

今回の PyMC化 はテキストと近い結果になりました。
ではでは、PyMCのベイズモデリングの世界を楽しんでまいりましょう!
テキストの紹介、引用表記、シリーズまえがき、PyMC等のバージョン情報は、このリンクの記事をご参照ください。
テキストで使用するデータは、R・Stan等のサンプルスクリプトとともに、出版社サイトからダウンロードして取得できます。
サマリー
テキストの概要
執筆者 : 山田剛史 先生
モデル難易度: ★★★・・ (ふつう)
自己評価
評点
$$
\begin{array}{c:c:c}
実装精度 & ★★★★・ & ほぼ納得 \\
結果再現度 & ★★★★・ & あと一歩 \\
楽しさ & ★★★★★ & 楽しい! \\
\end{array}
$$

評価ポイント
なんとかテキストに近い結果を得られました。
実はこの章を3~4周やり直ししたのですが、当初はベイズ推論結果が全く明後日の方向を向いており、「最終回の有終の美が遠い存在」に見えていました。
不本意な状態でブログ原稿に着手して、改めてPyMCコードを流し、モデル内の変数の評価値を「eval()」で確認したところ、重大なミス(しかも凡ミス)を発見!
ようやくちゃんとしたモデルに到達することができました。
粘って良かったです\(^o^)/
工夫・喜び・反省
ベイズモデル自体は一般的な階層モデルなので理解しやすかったです。
一方で実験計画~マルチレベルモデルといった統計界隈の理論が今ひとつ理解できなくて、専門用語が階層モデルと結びつかず、テキストの読解に難儀しました。
理論的基礎力を付けねばと一人納得して、心を新たにしました。

モデルの概要
テキストの調査・実験の概要
■ ざっくり劇場
この章のシナリオは、「単一事例実験計画のひとつ、参加者マルチベースラインデザイン」による実験から得た「単一事例実験データ」について、そのマルチ性・階層構造を統計モデル「マルチレベルモデル」と照合したのちに、「ベイズ階層モデル」に展開する、ことに尽きます。
もっとまとめると「参加者マルチベースラインデザイン実験から得たデータをベイズ階層モデルで解析しよう!」ということです。

テキストで用いるデータを眺めながら、主要用語をたどっていきましょう。
■ テキストで用いる単一事例実験データ~テキストの図19.5
テキストの216ページに掲載された「Lambert et al. (2006) の単一事例実験データ」の図を模しました。
この章のモデリングで用いるデータです。
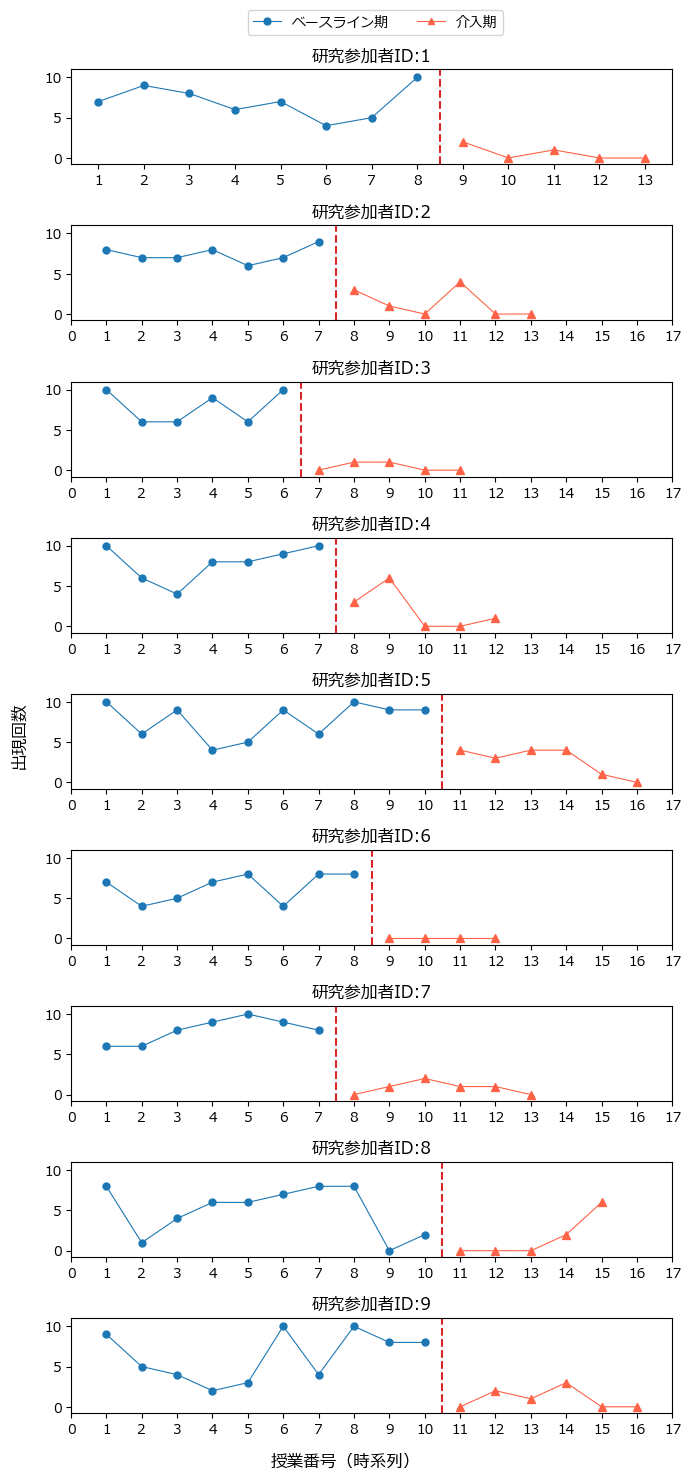
この実験データはテキストによると、算数の授業中の破壊的行動の出現回数を授業番号(時系列)ごとに測定しています。
青色のベースライン期の測定後、介入を実施してオレンジ色の介入期の測定を継続しています。
1回の授業における測定機会が10回あるので、出現回数の最大値は10です。
9名の研究参加者ごとにグラフ描画されています。
グラフの横軸は時系列であり、ここでは時間的な系列のある「授業番号」です。
縦軸は破壊的行動の出現回数です。
介入期では反応カードが用いられたとのこと(反応カードとは?)。
介入によって破壊的行動回数が減少している感じがします。
この図を頭の片隅に置きつつ、専門用語の旅へ出発です。
■ 単一事例実験計画~参加者マルチベースラインデザインへ
実験デザイン分野の話です。
① 単一事例実験計画
単一事例実験計画は「たった1つのケース」に対し何らかの処置を施し、その前後での反応を比較する手法、だそうです。
ケースには研究参加者個人のほか、グループ、クラスなどの1つのまとまりも含まれるそうです。
リアルに1件しか実験しないかというと、そうではないらしいです。
テキストの単一事例実験データでは、9人の研究参加者($${n=9}$$)の単一事例実験を扱っています。
② ABデザイン
1つのベースライン期(A)と1つの介入期(B)からなる実験デザインを「ABデザイン」と呼ぶそうです。
次の図のように、ベースライン期で一定回数の測定を行い、介入後の介入期も測定が繰り返されます。

③ 参加者マルチベースラインデザイン
ABデザインが複数ある場合をマルチベースラインデザインと呼ぶようです。
複数ある「層」ごとに介入開始時点が異なる点がこのデザインのポイントとのこと。
次の図のように複数の研究参加者がいて、各研究参加者について異なる時点で介入が開始されるデザインを「参加者マルチベースラインデザイン」と呼びます。

テキストの単一事例実験データは研究参加者9名の「参加者マルチベースラインデザイン」によるものです。
■ 単一事例実験データとマルチレベルモデル
単一事例実験データは「単一事例実験」から得たデータです。
マルチレベルモデルは統計モデルです。
データと統計モデルの関係性をテキストは丁寧に説明しています。
① 単一事例実験データのデータ的特徴
テキストは「単一事例実験データは研究参加者に測定時期が紐付くような階層構造を持つ」と説明します。
次の図はテキストの図19.4改造版です。
最上部の C は研究参加者(case)、中段の m は測定時期(session)、勝手に付与した Y は従属変数(破壊的行動の出現回数)です。

記号を日本語に置き換えてみました。

研究参加者と測定時期が階層構造であるとテキストは説明します。
単一事例実験データは階層構造を持つ、ということです。
② 階層構造とマルチレベルモデル
ここで「単一事例実験データの階層構造」と「統計モデルのマルチレベルモデルのレベル」のマリアージュ!
単一事例実験データの測定時期がマルチレベルモデルのレベル1、研究参加者がレベル2になります。
統計モデルのマルチレベルモデルのイメージです(数式)。
誤差項の従う分布等の表記は省略しています。
レベル1:
$${Y_{ij} = \beta_{0j} + \beta_{1j} X_{ij} + e_{ij} }$$
レベル2:
$${\beta_{0j} = \theta_{00} + u_{0j}}$$
$${\beta_{1j} = \theta_{10} + u_{1j}}$$
レベル1は測定時期$${i}$$、研究参加者$${j}$$の破壊的行動出現回数$${Y_{ij}}$$の回帰式イメージです。
切片$${\beta_{0j}}$$と傾き$${\beta_{1j}}$$は研究参加者単位です。
粒度に測定時期を含んでいるので、レベル1は測定時期単位なのです!ということなのかな?(研究参加者&測定時期の粒度のような・・・)
レベル2ではこれら切片$${\beta_{0j}}$$・傾き$${\beta_{1j}}$$の回帰式イメージを記載しています。
レベル2は研究参加者単位なのです!
この例では全研究参加者の平均値$${\theta_{00},\ \theta_{10}}$$に誤差項$${u_{0j},\ u_{1j}}$$が加算されています。
そしてテキストのモデルに続きます。

テキストのモデリング
1.通常のマルチレベルモデル
上記のマルチレベルモデルのイメージからテキストのマルチレベルモデルへ転換しましょう。
目的変数$${Y_{ij}}$$を連続変数とみなしたモデリングです。
$$
\begin{align*}
Y_{ij} &\sim \text{Normal}\ (\mu_{ij},\ \sigma^2_e) \\
\mu_{ij} &= \beta_{0j} + \beta_{1j} Phase_{ij} \\
\\
\beta_{0j} &= \theta_{00} + u_{0j} \\
\beta_{1j} &= \theta_{10} + u_{1j} \\
\\
\left(\begin{matrix}
u_{0j} \\ u_{1j}
\end{matrix}\right)
&\sim \text{MultivariateNormal} \left(
\left(\begin{matrix}
0\\0 \\
\end{matrix}\right),
\left(\begin{matrix}
\sigma^2_{u0} & \sigma_{u01} \\ \sigma_{u01} & \sigma^2_{u1} \\
\end{matrix}\right)
\right)
\end{align*}
$$
【変数の概要】
$${Y_{ij}}$$:授業番号(時系列)$${i}$$、研究参加者$${j}$$の出現回数
$${Phase_{ij}}$$:ベースライン期(0)か介入期(1)かを示すダミー変数
$${\beta_{0j}}$$:研究参加者単位のベースライン期のレベル
$${\beta_{1j}}$$:研究参加者単位の介入効果
$${\theta_{00}}$$:平均的なベースラインのパフォーマンス
$${\theta_{10}}$$:平均的な介入効果
$${u_{0j},\ u_{1j}}$$:研究参加者単位のランダムなバラツキ
なお、このモデルを用いたベイズモデリングは行いません。
その代わりにテキストの R スクリプトに書かれた統計的な分析を行います。
formula で次のように記述されるモデルです。
case は研究参加者です。
$$
Y \sim 1 + Phase + (1 + Phase\ |\ case)
$$
2.階層ベイズモデル
1.の通常のマルチレベルモデルを目的変数$${Y_{ij}}$$をカウントデータとするモデルに転換します。
このモデルでベイズ推論を行います。
■ 目的変数と関心のあるパラメータ
目的変数は、授業番号(時系列)$${i}$$、研究参加者$${j}$$の出現回数$${Y_{ij}}$$です。
関心のあるパラメータは全研究参加者の平均値である$${\theta_{00},\ \theta_{10}}$$です。
■ モデル数式
尤度関数が二項分布に変わりました。
$$
\begin{align*}
Y_{ij} &\sim \text{Binomial}\ (10,\ \pi_{ij}) \\
\text{logit}\ (\pi_{ij}) &= \log\ \left(\cfrac{\pi_{ij}}{1 - \pi_{ij}} \right) = \beta_{0j} + \beta_{1j} Phase_{ij} \\
\\
\beta_{0j} &= \theta_{00} + u_{0j} \\
\beta_{1j} &= \theta_{10} + u_{1j} \\
\\
\left(\begin{matrix}
u_{0j} \\ u_{1j}
\end{matrix}\right)
&\sim \text{MultivariateNormal} \left(
\left(\begin{matrix}
0\\0 \\
\end{matrix}\right),
\left(\begin{matrix}
\sigma^2_{u0} & \sigma_{u01} \\ \sigma_{u01} & \sigma^2_{u1} \\
\end{matrix}\right)
\right)
\end{align*}
$$
【変数の概要】
$${\pi_{ij}}$$:授業番号・研究参加者単位の成功確率(二項分布のパラメータ)
■分析・分析結果
分析の仕方や分析数値はテキストの記述が正確だと思いますので、テキストの読み込みをおすすめします。
PyMCの自己流モデルの推論値を利用した分析は「PyMC実装」章をご覧ください。
PyMC実装
Let's enjoy PyMC & Python !
準備・データ確認
1.インポート
### インポート
# 数値・確率計算
import pandas as pd
import numpy as np
# 統計処理
import statsmodels.formula.api as smf
# PyMC
import pymc as pm
import pytensor.tensor as pt
import bambi as bmb
import arviz as az
# 描画
import matplotlib.pyplot as plt
import seaborn as sns
plt.rcParams['font.family'] = 'Meiryo'
# グラフ描画
from graphviz import Graph
# ユーティリティ
import pickle
# ワーニング表示の抑制
import warnings
warnings.simplefilter('ignore')
2.説明用図表の作成
単一事例実験データの階層構造の図です。
graphviz の無向グラフを利用しました。
テキストの図19.3の改造版から。
### 単一事例実験データの階層構造のイメージ by graphviz
## 設定 neatoは頂点の位置を指定できる
g = Graph(engine='neato')
# nodeの基本属性の設定 shape='none'はノードの輪郭線無しの設定
g.attr('node', shape='none')
## node:頂点の作成
g.node('C1', pos='1, 2!')
g.node('C2', pos='3, 2!')
g.node('C3', pos='5, 2!')
g.node('.C', pos='6, 2!', label='…')
g.node('Cj', pos='7, 2!')
g.node('m11', pos='0.5, 1!')
g.node('.1', pos='1, 1!', label='…')
g.node('mi1', pos='1.5, 1!')
g.node('m12', pos='2.5, 1!')
g.node('.2', pos='3, 1!', label='…')
g.node('mi2', pos='3.5, 1!')
g.node('m13', pos='4.5, 1!')
g.node('.3', pos='5, 1!', label='…')
g.node('mi3', pos='5.5, 1!')
g.node('m1j', pos='6.5, 1!')
g.node('.4', pos='7, 1!', label='…')
g.node('mij', pos='7.5, 1!')
g.node('Y11', pos='0.5, 0!')
g.node('Yi1', pos='1.5, 0!')
g.node('Y12', pos='2.5, 0!')
g.node('Yi2', pos='3.5, 0!')
g.node('Y13', pos='4.5, 0!')
g.node('Yi3', pos='5.5, 0!')
g.node('Y1j', pos='6.5, 0!')
g.node('Yij', pos='7.5, 0!')
# ## edge:辺の作成, labelで辺にラベル値を表示
g.edge('C1', 'm11')
g.edge('C1', 'mi1')
g.edge('C2', 'm12')
g.edge('C2', 'mi2')
g.edge('C3', 'm13')
g.edge('C3', 'mi3')
g.edge('Cj', 'm1j')
g.edge('Cj', 'mij')
g.edge('m11', 'Y11', style='dashed')
g.edge('mi1', 'Yi1', style='dashed')
g.edge('m12', 'Y12', style='dashed')
g.edge('mi2', 'Yi2', style='dashed')
g.edge('m13', 'Y13', style='dashed')
g.edge('mi3', 'Yi3', style='dashed')
g.edge('m1j', 'Y1j', style='dashed')
g.edge('mij', 'Yij', style='dashed')
## グラフの描画
g【実行結果】

もう1つの階層図です。
### 使用データの階層構造のイメージ by graphviz
## 設定 neatoは頂点の位置を指定できる
g = Graph(engine='neato')
# nodeの基本属性の設定 shape='none'はノードの輪郭線無しの設定
g.attr('node', shape='none')
## node:頂点の作成
g.node('参加者1', pos='1, 2!')
g.node('参加者2', pos='3, 2!')
g.node('参加者3', pos='5, 2!')
g.node('.C', pos='6, 2!', label='…')
g.node('参加者j', pos='7, 2!')
g.node('授業11', pos='0.5, 1!')
g.node('.1', pos='1, 1!', label='…')
g.node('授業i1', pos='1.5, 1!')
g.node('授業12', pos='2.5, 1!')
g.node('.2', pos='3, 1!', label='…')
g.node('授業i2', pos='3.5, 1!')
g.node('授業13', pos='4.5, 1!')
g.node('.3', pos='5, 1!', label='…')
g.node('授業i3', pos='5.5, 1!')
g.node('授業1j', pos='6.5, 1!')
g.node('.4', pos='7, 1!', label='…')
g.node('授業ij', pos='7.5, 1!')
g.node('回数11', pos='0.5, 0!')
g.node('回数i1', pos='1.5, 0!')
g.node('回数12', pos='2.5, 0!')
g.node('回数i2', pos='3.5, 0!')
g.node('回数13', pos='4.5, 0!')
g.node('回数i3', pos='5.5, 0!')
g.node('回数1j', pos='6.5, 0!')
g.node('回数ij', pos='7.5, 0!')
# ## edge:辺の作成, labelで辺にラベル値を表示
g.edge('参加者1', '授業11')
g.edge('参加者1', '授業i1')
g.edge('参加者2', '授業12')
g.edge('参加者2', '授業i2')
g.edge('参加者3', '授業13')
g.edge('参加者3', '授業i3')
g.edge('参加者j', '授業1j')
g.edge('参加者j', '授業ij')
g.edge('授業11', '回数11', style='dashed')
g.edge('授業i1', '回数i1', style='dashed')
g.edge('授業12', '回数12', style='dashed')
g.edge('授業i2', '回数i2', style='dashed')
g.edge('授業13', '回数13', style='dashed')
g.edge('授業i3', '回数i3', style='dashed')
g.edge('授業1j', '回数1j', style='dashed')
g.edge('授業ij', '回数ij', style='dashed')
## グラフの描画
g【実行結果】


3.データの読み込み
csvファイル「lambert.csv」をpandasのデータフレームに読み込みます。
### データの読み込み
# case:研究参加者ID, session:授業番号, y:出現回数(目的変数), phase:BL期0, 介入期:1
data = pd.read_csv('lambert.csv')
display(data)【実行結果】
項目内容の概要です。
・case:研究参加者ID
・sesson:授業番号(時系列)
・y:破壊的行動の出現回数(目的変数)
・phase:ベースライン期の場合 0、介入期の場合 1 のダミー変数

4.データの概観の確認
要約統計量を確認しましょう。
### 要約統計量の表示
data.describe().round(1)【実行結果】
時系列データ、かつ、ベースライン期と介入期で異なる特徴のあるデータなので、単純な統計量から読み取れることは少ないかもです。

研究参加者別に時系列プロットを描画します。
テキストの図19.5に相当します。
### 時系列プロットの描画 ※図19.5に相当
# 描画領域の指定
fig, ax = plt.subplots(9, 1, figsize=(7, 15), sharey=True)
# 研究参加者IDごとに描画を繰り返し処理
for i in range(0, 9):
# 研究参加者1人分のデータを取り出し
tmp = data[data['case']==i+1]
# 時系列折れ線グラフの描画
ax[i].plot(tmp[tmp['phase']==0]['session'], tmp[tmp['phase']==0]['y'], '-o',
lw=0.8, ms=5, color='tab:blue')
ax[i].plot(tmp[tmp['phase']==1]['session'], tmp[tmp['phase']==1]['y'], '-^',
lw=0.8, color='tomato')
# 介入開始時点を示す赤点線の描画
ax[i].axvline(tmp[tmp['phase']==1]['session'].min()-0.5, ls='--',
color='tab:red')
# 修飾(axesレベル)
ax[i].set(title=f'研究参加者ID:{i+1}', ylim=(-0.8, data['y'].max()+1),
xticks=range(0, 18))
# 凡例(凡例用のダミープロットを実施)
ax[0].plot([], [], '-o', lw=0.8, ms=5, color='tab:blue', label='ベースライン期')
ax[0].plot([], [], '-^', lw=0.8, ms=5, color='tomato', label='介入期')
ax[0].legend(ncols=2, bbox_to_anchor=(0.73, 1.7), loc='upper right')
# 修飾(figレベル)
# fig.suptitle('単一事例実験データ')
fig.supxlabel('授業番号(時系列)')
fig.supylabel('出現回数')
plt.tight_layout();【実行結果】
赤い点線が介入時点です。
研究参加者によって授業期間の長さが異なるようです。
介入後は出現回数が減少している感じがします。

研究参加者別・介入あり・なし別に箱ひげ図を描画します。
### 箱ひげ図の描画
plt.figure(figsize=(8, 4))
sns.boxplot(data=data, x='case', y='y', hue='phase', fill=None, legend=True)
plt.title('フェーズ別出現回数 フェーズ0:ベースライン期, 1:介入期')
plt.legend(title='phase', bbox_to_anchor=(1, 1));【実行結果】
phase=0(青色)がベースライン期、phase=1(オレンジ色)が介入期です。
介入期の出現回数が大きく減った(というよりもベースライン期の出現回数が多すぎ!?)ように見えます。
介入の効果があるように感じます。


プレ分析
テキストの掲載はありませんが、R スクリプト内で統計的な分析を実行しています。
Pythonで真似してみましょう。
1.線形混合モデル(LMM)
R の lmer による「y ~ 1 + phase + (1 + phase | case)」の分析を真似ます。
以下は R の lmer の分析結果サマリーです。

Python は statsmodels の mixedlm の出番です!
### 線形混合モデルの定義と分析実行 ※Rスクリプトの「2 level multilevel model」
# モデルの定義
model_lmm = smf.mixedlm(
formula='y ~ 1 + phase', # y ~ 1 + phase + (1 + phase | case)
data=data,
groups=data['case'],
re_formula='1 + phase'
)
# 分析の実行
result_lmm = model_lmm.fit()
# 結果の表示
print(result_lmm.summary())【実行結果】
出力項目が R のサマリーと異なるので、どう比べていいのか分かりかねます…。

下段の Intercept と phase は固定効果(Fixed Effects)です。
R の係数の推定値とほぼ同じ結果です。
【R の固定効果】

標準化残差をなんとか拵えました。
ただし適切な算出かは不明です。
### 標準化残差の分布
# 残差の平均値
resid_mean = result_lmm.resid.mean()
# 残差の標準偏差
resid_std = result_lmm.resid.std(ddof=0)
# 残差の標準化
resid_scaled = (result_lmm.resid - resid_mean) / resid_std
# データフレーム形式で結果表示
resid_scaled.describe().to_frame().T.set_axis(['value'], axis=0).round(4)【実行結果】

【R の規格化残差(Scales residuals)】

これにて終了!

2.一般化線形混合モデル(GLMM)
R の glmer による「y ~ 1 + phase + (1 + phase | case)」の分析を真似ます。
ファミリーはポアソン分布です。
以下は R の glmer の分析結果サマリーです。

Python は GLMM が苦手です(当社比)。
何となく GLMM ができそうなライブラリ gpboost で試してみます。
使い方があっているかどうか、および、これで GLMM 分析ができているかは謎です。
gpboost と patsy の dmatrix をインポートします。
patsy は statsmodels の裏でも利用されている formula 記述対応ライブラリです。
### 追加インポート
import gpboost as gpb
from patsy import dmatrixそれでは GLMM(ようなもの)を実行します!
gpboost による GLMM の学習には scikit-learn 似のインターフェイスが用意されています。
### 線形混合モデルの定義と分析実行
# ※Rスクリプトの「Multilevel generalized linear model」
# 目指すformula: y ~ 1 + phase + (1 + phase | case)
# 変数の設定
y = data['y'] # 目的変数
X = dmatrix('1 + phase', data=data) # 1 + phase の部分
group = data['case'] # (1 + phase | case)のグループ
family = 'poisson' # 尤度
# モデルの定義
model_glmm = gpb.GPModel(group_data=group, likelihood=family)
# モデルのフィット
model_glmm.fit(y=y, X=X, params={'std_dev':True})
# サマリーの表示
model_glmm.summary()【実行結果】
「ひとまず実行した」というレベル感で終了です。
(R の分析結果との照合には進みません)

プレ分析は以上です。

モデルの構築
テキストはベイズモデル構築に brms を用いているので、Python の Bambi を利用しようか悩みましたが、Bambi の事前分布で多変量正規分布を定義する方法を考えつかなかったので、あっさり PyMC を使うことに決めました。
モデルの数式表現
目指したいPyMCのモデルの雰囲気を混ぜた「なんちゃって数式」表記です。
$$
\begin{align*}
\theta_{00} &\sim \text{Uniform}\ (\text{lower}=-100,\ \text{upper}=100) \\
\theta_{10} &\sim \text{Uniform}\ (\text{lower}=-100,\ \text{upper}=100) \\
\\
\rho &\sim \text{Uniform}\ (\text{lower}=-1,\ \text{upper}=1) \\
\sigma_{u0} &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=100) \\
\sigma_{u1} &\sim \text{Uniform}\ (\text{lower}=0,\ \text{upper}=100) \\
cov_{u01} &= \sigma_{u0} \times \sigma_{u0} \times \rho \\
cov &= \text{pt.stack}([[\sigma_{u0}^2, cov_{u01}], [cov_{u01}, \sigma_{u1}^2]]) \\
u &\sim \text{MvNormal}\ (\text{mu}=[0,0],\ \text{cov}=cov,\ shape=(9,2)) \\
\\
\beta_0 &= \theta_{00} + u[:, 0],\ \text{dims}= id \\
\beta_1 &= \theta_{10} + u[:, 1],\ \text{dims}= id \\
\\
\pi &= \text{invlogit}\ (\beta_0[idIdx] + \beta_1[idIdx] \times phase) \\
likelihood &\sim \text{Binomial}\ (\text{n}=10,\ \text{p}=\pi) \\
\end{align*}
$$

1.モデルの定義
数式表現を実直にモデル記述します。
### モデルの定義
with pm.Model() as model:
### coordの定義
# データのインデックス
model.add_coord('data', values=data.index, mutable=True)
# 研究参加者ID
model.add_coord('id', values=sorted(data['case'].unique() - 1),
mutable=True)
### dataの定義
# 目的変数
y = pm.ConstantData('y', value=data['y'].values, dims='data')
# フェーズのインデックス
phase = pm.ConstantData('phase', value=data['phase'].values,
dims='data')
# 研究参加者IDのインデックス(0始まり)
idIdx = pm.ConstantData('idIdx', value=data['case'].values - 1,
dims='data')
### 事前分布
## 研究参加者単位の切片に含まれる平均的なベースラインのパフォーマンス
theta00 = pm.Uniform('theta00', lower=-100, upper=100)
## 研究参加者単位の傾きに含まれる平均的な介入効果
theta10 = pm.Uniform('theta10', lower=-100, upper=100)
## 研究参加者単位の切片と傾きに含まれる誤差u
# 分散共分散行列を構成する相関係数、標準偏差の事前分布
rho = pm.Uniform('rho', lower=-1, upper=1)
sigmaU0 = pm.Uniform('sigmaU0', lower=0, upper=100)
sigmaU1 = pm.Uniform('sigmaU1', lower=0, upper=100)
# 共分散covU01(テキストのσ_u01)
covU01 = pm.Deterministic('covU01', sigmaU0*sigmaU1*rho)
# 分散共分散行列cov
cov = pt.stacklists([[sigmaU0**2, covU01],
[covU01, sigmaU1**2]])
# 誤差u
u = pm.MvNormal('u', mu=[0, 0], cov=cov, shape=(9, 2))
# レベル2:研究参加者単位の切片と傾き
beta0 = pm.Deterministic('beta0', theta00 + u[:, 0], dims='id')
beta1 = pm.Deterministic('beta1', theta10 + u[:, 1], dims='id')
# 確率pi 逆ロジット関数
pi = pm.Deterministic('pi',
pm.invlogit(beta0[idIdx] + beta1[idIdx] * phase),
dims='data')
### 尤度:二項分布
likelihood = pm.Binomial('likelihood', n=10, p=pi, observed=y, dims='data')【モデル注釈】
coordの定義
座標に名前を付けたり、その座標が取りうる値を設定できます。
今回は次の2つを設定しました。データの行の座標:名前「data」、値「行インデックス」
研究参加者の座標:名前「id」、値「研究参加者ID」
dataの定義
次の3つを設定しました。出現回数:y (目的変数)
ベースライン期か介入期かを示すダミー変数:phase
研究参加者のインデックス:idIdx
パラメータの事前分布
モデルの数式表現どおりです。
尤度
二項分布です。
2.モデルの外観の確認
### モデルの表示
model【実行結果】

### モデルの可視化
pm.model_to_graphviz(model)【実行結果】
中段の id ~研究参加者単位の beta0、beta1 を核にして連なる階層構造が輝いて見えます。


3.事後分布からのサンプリング
乱数生成数はテキストよりも少ないです。
nuts_sampler='numpyro'とすることで、numpyroをNUTSサンプラーに利用できます。
処理時間はおよそ30秒でした。
### 事後分布からのサンプリング ※NUTSサンプラーにnumpyroを使用 30秒
# テキスト: iter=10000, warmup=5000, chains=4
with model:
idata = pm.sample(draws=1000, tune=1000, chains=4, target_accept=0.98,
nuts_sampler='numpyro', random_seed=1234)【実行結果】省略
4.サンプリングデータの確認
$${\hat{R}}$$、トレースプロットを確認します。
事後分布の収束確認は$${\hat{R} \leq 1.1}$$とします。
ここでは$${\hat{R} > 1.01}$$のパラメータが無いことを確認します。
### r_hat>1.1の確認
# 設定
idata_in = idata # idata名
threshold = 1.01 # しきい値
# しきい値を超えるR_hatの個数を表示
print((az.rhat(idata_in) > threshold).sum())【実行結果】
$${\hat{R} > 1.01}$$のパラメータは0件でした。
全てのパラメータが$${\hat{R} \leq 1.1}$$であることを確認できました。

ざっくり事後分布サンプリングデータの要約統計量とトレースプロットを確認します。
### 推論データの要約統計情報の表示
pm.summary(idata, hdi_prob=0.95, round_to=3)【実行結果】

トレースプロットで事後分布サンプリングデータの様子を確認します。
### トレースプロットの表示
pm.plot_trace(idata, compact=True)
plt.tight_layout();【実行結果】
左のグラフから、4本のマルコフ連鎖chainがほぼ同じ分布であることが分かります。
右のグラフでは線が満遍なく描画されています。
収束していると思われます。

5.推論データの保存
推論データを再利用する(かもしれない)場合に備えてファイルに保存しましょう。
idata をpickleで保存します。
### idataの保存 pickle
file = r'idata_ch19.pkl'
with open(file, 'wb') as f:
pickle.dump(idata, f)読み込みコードは次のとおりです。
### idataの読み込み pickle
file = r'idata_ch19.pkl'
with open(file, 'rb') as f:
idata_load = pickle.load(f)

分析
パラメータの事後統計量を算出します。
テキストの表19.1に相当します。
### パラメータの推定結果 ※表19.1に相当
## 事後統計量算出関数の定義
def calc_stats(x):
ci = np.quantile(x, q=[0.025, 0.5, 0.975])
return np.mean(x), ci[1], np.std(x), ci[0], ci[2]
## 事後統計量の算出
stats_df = pd.DataFrame({
'θ_00':
calc_stats(idata.posterior.theta00.stack(sample=('chain', 'draw')).data),
'θ_10':
calc_stats(idata.posterior.theta10.stack(sample=('chain', 'draw')).data),
'σ_u0':
calc_stats(idata.posterior.sigmaU0.stack(sample=('chain', 'draw')).data),
'σ_u1':
calc_stats(idata.posterior.sigmaU1.stack(sample=('chain', 'draw')).data),
'σ_u01':
calc_stats(idata.posterior.covU01.stack(sample=('chain', 'draw')).data)
}, index=['EAP', 'MED', 'SD', '2.5%CI', '97.5%CI']).T
display(stats_df.round(2))【実行結果】
最終行の$${\sigma_{u01}}$$(共分散)が若干ずれていますが、他のパラメータの推定値はテキストとほぼ一致しています!

テキストの217~218ページで介入の効果を吟味しています。
テキストにならって数値を追いましょう。
切片のEAP推定値$${\hat{\theta}_{00}=0.89}$$はベースライン期の平均的な破壊的行動の対数オッズです。
逆ロジット関数(標準シグモイド関数)で確率の単位に変換しましょう。
### ベースライン期の破壊的行動の確率 テキスト218ページ
# ロジット変換関数の定義
# prob_func = lambda x: 1 / (1 + np.exp(-x)) # こちらでもOK(標準シグモイド関数)
prob_func = lambda x: np.exp(x) / (1 + np.exp(x))
# 確率の算出
log_odds = stats_df.loc['θ_00', 'EAP']
print('ベースライン期に平均的に破壊的行動が見られる確率: '
f'{prob_func(log_odds):.2f}')【実行結果】
テキストの計算値と合いました。

続いて係数のEAP推定値$${\hat{\theta}_{10}=-3.15}$$は介入効果を表す対数オッズです。
逆ロジット関数(標準シグモイド関数)で確率の単位に変換しましょう。
### 介入期の破壊的行動の確率 テキスト218ページ
# 確率の算出
log_odds = stats_df.loc['θ_00', 'EAP'] + stats_df.loc['θ_10', 'EAP']
print(f'介入期に平均的に破壊的行動が見られる確率: {prob_func(log_odds):.2f}')【実行結果】
テキストの計算値とほぼ合いました。

【分析~テキストにならって】
ベースライン期には平均的に$${0.71}$$の確率で破壊的行動が観察されました。
介入期には平均的に$${0.09}$$の確率で破壊的行動が観察されることになりました。
ベースライン期に比べて介入期の破壊的行動の出現に大きな減少がみられます。
このことは、介入の効果を示唆しています。

以上で第19章は終了です。
19章は最終章ですので、たのしいベイズモデリング2の写経ブログはこれにて終了となります。
長期間にわたるご愛顧、誠にありがとうございました。

おわりに
たのしいベイズモデリング3!?
たのしいベイズモデリングの発行は2018年10月、たのしいベイズモデリング2の発行は2019年11月です。
「2」の発行からすでに4年半が経過しましたが、待望の「たのしいベイズモデリング3」はいつ頃発行されるのでしょう!?
2019年以降、データ分析手法は多種多様に大発展しています。
新しいモデルの提案、統計・データ分析ライブラリの充実などなど。
さらには大規模言語モデル(ChatGPT的なアレです)の急進に伴って、自然言語処理界隈が賑やかになっています。
AI時代のたのしいベイズモデリングにはどのようなトピックが描かれるのでしょう。
誰がベイズモデリングの主役に立つのでしょう!?

おわり
シリーズの記事
次の記事

前の記事
目次
ブログの紹介
note で7つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。
2.実験!たのしいベイズモデリング1&2をPyMC Ver.5で
書籍「たのしいベイズモデリング」・「たのしいベイズモデリング2」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.実験!岩波データサイエンス1のベイズモデリングをPyMC Ver.5で
書籍「実験!岩波データサイエンスvol.1」の4人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう!
4.楽しい写経 ベイズ・Python等
ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀
5.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん!
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。
6.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
7.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
最後までお読みいただきまして、ありがとうございました。
