
「回帰分析から学ぶ計量経済学」をPythonで写経 ~ 第5章「時系列分析」②季節性・自己回帰モデル
第5章「時系列分析」
書籍の著者 山澤成康 先生
この記事は、書籍「回帰分析から学ぶ計量経済学」第5章「時系列分析」の Python写経活動 を取り扱います。
今回は時系列分析のテーマのうち、季節性とAR(自己回帰モデル)を取り扱います。
では書籍を開いて回帰分析の旅に出発です🚀

はじめに
書籍「回帰分析から学ぶ計量経済学」のご紹介
このシリーズは書籍「回帰分析から学ぶ計量経済学: Excelで読み解く経済のしくみ」(オーム社、「テキスト」と呼びます)の Python 写経です。
テキストは、2023年11月に発売され、副題「Excelで読み解く経済のしくみ」のとおり、主に Excel を用いて、計量経済学を平易に学べる素晴らしい書籍です。
テキストの「はじめに」に著者の先生が執筆の動機を書かれています。
社会人の統計リテラシーの向上をテーマの1つとした科研費プロジェクトの最終年度で、広く社会人に向けてわかりやすい経済分析の本を書きたかったのです。
私にとって計量経済学は高嶺の花ですが、このテキストでさまざまな回帰分析のアプローチを知ることができました。
また、書籍の Excel 処理を Python に置き換える「寄り道写経」の実践を通じて、回帰分析のお気持ちに少し近づけた感じがいたします。
回帰分析に慣れ親しむのに丁度良いレベル感と内容ですので、これはぜひともブログにしたい!と思って現在に至ります。
計量経済学の色を薄め、データ分析の色を濃いめに書いてまいります!

引用表記
この記事は、出典に記載の書籍に掲載された文章と配布データを引用し、適宜、掲載文章・配布データを改変して書いています。
【出典】
「回帰分析から学ぶ計量経済学: Excelで読み解く経済のしくみ」
第1版第1刷、著者 山澤成康、オーム社
記事中のイラストは、「かわいいフリー素材集いらすとや」さんのイラストをお借りしています。
ありがとうございます!
第5章 時系列分析
この記事は第5章の以下の節を取り扱います。
5.4 季節性を除くには(季節調整、季節ダミー、前年比・前期比)
5.7 ARIMAモデル
5.8 日銀短観をAR推定する
記事に用いるデータは、オーム社の書籍紹介サイトからダウンロードできる Excel ファイル内のデータをもとにしてCSVファイルを作成し、data フォルダに格納しています。
第5章で用いるライブラリをインポートします。
### インポート
# 数値計算
import numpy as np
import pandas as pd
# 統計処理
import scipy.stats as stats
import statsmodels.formula.api as smf # フォーミュラ構文
import statsmodels.tsa.api as tsa # 時系列
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf # コレログラム等
import pmdarima as pm # ARIMA次数自動探索
import lmdiag # 残差プロット
# 描画
import matplotlib.pyplot as plt
import seaborn as sns
import japanize_matplotlib
# ワーニング非表示
import warnings
warnings.simplefilter('ignore')
5.4 季節性を除くには(季節調整、季節ダミー、前年比・前期比)
■ 季節性を除く方法 p.159
テキストによると季節性のあるデータは分析しにくいとし、季節性を除く2つの方法を提示しています。
・前年同期比をみること
・データから季節要因を取り除いた「季節調整値」を使うこと
■ 季節調整値の基本的な考え方 p.159
テキストは、時系列データを$${T}$$:すう勢(Trend)変動、$${C}$$:循環(Cycle)変動、$${S}$$:季節(Seasonal)変動、$${I}$$:不規則(Irregular)変動に分割することから季節調整値の算出ははじまるとし、現系列$${O}$$を分解する2つのモデルを紹介しています。
$$
乗法モデル\ O = T \times C \times S \times I \\
加法モデル\ O = T + C + S + I \\
$$

■ ヘンダーソン移動平均 p.159~
テキストは季節変動を除く基本的な方法は「移動平均」とし、当月周辺のウエイトを大きくした「ヘンダーソン移動平均」を紹介しています。
四半期実質GDPデータを用いて、当四半期と前後2四半期の全5四半期の中心移動平均をとり、以下のウエイトを乗じます。
$$
-0.073,\ 0.294,\ 0.558,\ 0.294,\ -0.073
$$
ではヘンダーソン移動平均を実践しましょう。
データを読み込みます。
### データの読み込み
# CSVファイルの読み込み
df2 = pd.read_csv('./data/05_02_gdp.csv', index_col=0)
# 四半期日付のインデックスを設定
df2.index = pd.date_range(start='1994-03-31', periods=df2.shape[0], freq='QE')
df2.index.name = '四半期'
# データフレームの表示
print('df2.shape:', df2.shape)
display(df2.head())【実行結果】
すでに季節調整値が設定されています。。。

テキスト通り、季節調整値に対してヘンダーソン移動平均をとります。
### ヘンダーソン移動平均の算出
## 設定と準備
# ヘンダーソン移動平均の重み
henderson_weight = np.array([-0.073, 0.294, 0.558, 0.294, -0.073])
# ヘンダーソン移動平均列の追加
df2['ヘンダーソン移動平均'] = np.nan
## ヘンダーソン移動平均の算出 季節調整値に対して加重移動平均を取る
for i in range(2, len(df2)-2):
df2.iloc[i, 2] = sum(df2.iloc[i-2:i+3, 1] * henderson_weight)
## 結果の表示
print('df2.shape: ', df2.shape)
display(df2)【実行結果】

可視化しましょう。
### 可視化
# 期間の抽出条件の設定
query = (df2.index >= '2016-09-30') & (df2.index <= '2022-09-30')
# 描画領域の設定
plt.figure(figsize=(10, 4))
# 3つのGDP値の折れ線グラフを描画, 描画順を変更する目的で列の順序を変えている
sns.lineplot(data=df2[query][['ヘンダーソン移動平均', '実質国内総生産(原系列)',
'実質国内総生産(季節調整値)']])
# 修飾 Y軸表示区間、Y軸ラベル、グラフタイトル、格子線
plt.ylim(110, 145)
plt.ylabel('実質GDP [兆円]')
plt.title('季節調整と移動平均')
plt.grid(lw=0.5)
plt.show()【実行結果】
青色のヘンダーソン移動平均は凸凹が減り、直線的な傾向を示しています。
2020年半ばには大きな落ち込みがあります。
おそらく新型ウイルス感染拡大に伴う一時的な減少と思われます。


5.7 ARIMAモデル
■ ARモデルとMAモデル p.162~
自己回帰モデル AR 、移動平均モデル MA 、差分 I をあわせて ARIMAモデルです!
テキストのAR(1)、AR(2)、MA(1)、MA(2)の数式をお借りします。
$$
\begin{align*}
AR(1)\quad Y &= a_0 + a_1 Y_{t-1} + u_t \\
AR(2)\quad Y &= a_0 + a_1 Y_{t-1} + a_2 Y_{t-2} + u_t \\
MA(1)\quad u_t &= \varepsilon_t + b_1 \varepsilon_{t-1} \\
MA(2)\quad u_t &= \varepsilon_t + b_1 \varepsilon_{t-1} + b_2 \varepsilon_{t-2} \\
\end{align*}
$$
括弧の数値は何期前までを使うかを示しています。
MAモデルは過去の誤差項$${\varepsilon_t}$$を参照しています。
テキストにならって、AR(1)系列データとMA(2)系列データを生成します。
乱数生成結果がテキストと異なるため、グラフ等もテキストと異なる結果になります。
### データの作成
## 設定と準備
T = 100 # サンプルサイズ
rng = np.random.default_rng(seed=8) # 乱数生成器
## データの作成
# 誤差項の作成 [-5, 5)の一様分布乱数
u = rng.uniform(low=-5, high=5, size=T)
# AR1の作成 0.5 * AR1_t-1 + u_t
AR1 = np.zeros(T)
for t in range(1, T):
AR1[t] = 0.5 * AR1[t-1] + u[t]
# MA2の作成 u_t + 0.2*u_t-1 - 0.5*u_t-2
MA2 = np.repeat(np.nan, T)
for t in range(2, T):
MA2[t] = u[t] + 0.2*u[t-1] - 0.5*u[t-2]
# MA1の作成 u_t + 0.5*u_t-1
MA1 = np.repeat(np.nan, T)
for t in range(1, T):
MA1[t] = u[t] + 0.5*u[t-1]
## データフレーム化
df3 = pd.DataFrame({'u': u, 'AR1': AR1, 'MA2': MA2, 'MA1': MA1},
index=range(1, T+1))
print('df3.shape: ', df3.shape)
display(df3)【実行結果】
テキストのExcelデータに存在するMA(1)系列データも作っています。

AR(1)系列データとMA(2)系列データを可視化します。
### 可視化
# 描画領域の設定
plt.figure(figsize=(10, 3))
# 折れ線グラフの描画
plt.plot(df3.AR1[:94], lw=0.9)
# 修飾
plt.xlabel('時間')
plt.title('AR1')
plt.grid(lw=0.5)【実行結果】

### 可視化
# 描画領域の設定
plt.figure(figsize=(10, 3))
# 折れ線グラフの描画
plt.plot(df3.MA2[:94], lw=0.9)
# 修飾
plt.xlabel('時間')
plt.title('MA2')
plt.grid(lw=0.5)【実行結果】

2つの系列データ、違いはよくわかりません。。。
(テキストにも同様のことが書かれていますね!)

■ コレログラム p.164
コレログラムを描画して、AR系列、MA系列の特徴を確認します。
statsmodels の plot_acf 関数と plot_pacf 関数を利用します。
描画関数を定義しておきます。
### コレログラムと偏自己相関関数プロットの描画関数
def plot_acf_pacf(x, lags):
# 描画領域の設定
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8, 3))
# コレログラムの描画
plot_acf(x, lags=lags, auto_ylims=True, zero=True, ax=ax1)
ax1.set(xlabel='lag', ylabel='ACF')
ax1.grid(lw=0.5)
# 偏自己相関関数プロットの描画
plot_pacf(x, lags=lags, auto_ylims=True, zero=True, ax=ax2)
ax2.set(xlabel='lag', ylabel='PACF')
ax2.grid(lw=0.5)
# 全体調整
plt.tight_layout()
plt.show()AR(1)系列データのコレログラム等を描画します。
### AR(1)のコレログラム・偏自己相関プロットの描画
plot_acf_pacf(df3.AR1, 20)【実行結果】
左がコレログラム、右が偏自己相関係数のプロットです。

コレログラムは徐々に減衰していて、偏自己相関係数はラグ1まで有意である(ラグ2以降は有意でない)状況です。
テキストによると、AR(p)系列は偏自己相関係数がラグ p+1 で切断されるとのこと。
MA(2)系列データのコレログラム等を描画します。
### MA(2)のコレログラム・偏自己相関プロットの描画
plot_acf_pacf(df3.MA2.dropna(), 20)【実行結果】
両方のグラフでラグ2が有意です(薄青色のゾーンを超えています)。
テキストによると、MA(q) 系列は自己相関係数(左のグラフ)がラグ q+1 で切断されるとのこと。


5.8 日銀短観をAR推定する
■ データの確認 p.165
テキストの日銀短観データを用いて、AR(1)、AR(2)、AR(3) で推定します。
データを読み込みます。
### データの読み込み
# CSVファイルの読み込み
df4 = pd.read_csv('./data/05_03_tankan.csv', index_col=0, parse_dates=[0])
# データフレームの表示
print('df4.shape:', df4.shape)
display(df4.head())
display(df4.tail())【実行結果】
1983年3月期から2022年12月期までの160四半期の業況判断DIデータです。

時系列折れ線グラフで可視化します。
### 可視化
# 描画領域の設定
plt.figure(figsize=(10, 3))
# 時系列折れ線グラフの描画
plt.plot(df4.DI)
# 修飾
plt.grid(lw=0.5)
plt.xlabel('時間 [四半期]')
plt.ylabel('業況判断DI')
plt.show()【実行結果】

データの前処理を行います。
ラグ1~3を追加します。
### データの前処理 ラグ1~3を追加
df4reg = df4.copy()
df4reg['一期前'] = df4reg['DI'].shift(1)
df4reg['二期前'] = df4reg['DI'].shift(2)
df4reg['三期前'] = df4reg['DI'].shift(3)
df4reg = df4reg.dropna()
print('df4reg.shape: ', df4reg.shape)
display(df4reg)【実行結果】


■ AR推定 p.165~
AR(1)~AR(3)の推定です。
statsmodels の ols で、DIを目的変数、ラグ1~3を説明変数にして回帰分析を行います。
AR(1)です。
### 回帰分析の実行 AR(1)
result = smf.ols(formula='DI ~ 一期前', data=df4reg).fit()
display(result.summary())【実行結果】

AR(2)です。
### 回帰分析の実行 AR(2)
result = smf.ols(formula='DI ~ 一期前 + 二期前', data=df4reg).fit()
display(result.summary())【実行結果】

AR(3)です。
### 回帰分析の実行 AR(3)
result = smf.ols(formula='DI ~ 一期前 + 二期前 + 三期前', data=df4reg).fit()
display(result.summary())【実行結果】
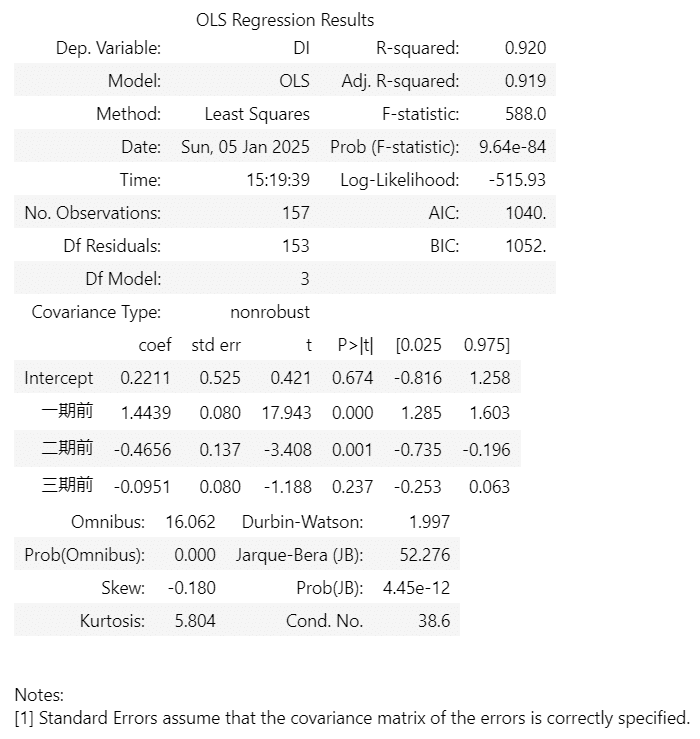
テキストの分析の通り、AR(2)モデルが最も良い、と判断しましょう。
自由度調整済み決定係数はAR(3)モデルが$${0.919}$$であり、最も高いです。
ただ、AR(2)モデルの決定係数は$${0.918}$$であり差は僅かです。
さらに、AR(3)モデルのラグ3の係数の$${t}$$値は$${-1.188}$$であり、$${5\%}$$水準で有意ではありません。
今回の写経は以上です。
シリーズの記事
次の記事

前の記事
目次
ブログの紹介
note で7つのシリーズ記事を書いています。
ぜひ覗いていってくださいね!
1.のんびり統計
統計検定2級の問題集を手がかりにして、確率・統計をざっくり掘り下げるブログです。
雑談感覚で大丈夫です。ぜひ覗いていってくださいね。
統計検定2級公式問題集CBT対応版に対応しています。
Python、EXCELのサンプルコードの配布もあります。
2.実験!たのしいベイズモデリング1&2をPyMC Ver.5で
書籍「たのしいベイズモデリング」・「たのしいベイズモデリング2」の心理学研究に用いられたベイズモデルを PyMC Ver.5で描いて分析します。
この書籍をはじめ、多くのベイズモデルは R言語+Stanで書かれています。
PyMCの可能性を探り出し、手軽にベイズモデリングを実践できるように努めます。
身近なテーマ、イメージしやすいテーマですので、ぜひぜひPyMCで動かして、一緒に楽しみましょう!
3.実験!岩波データサイエンス1のベイズモデリングをPyMC Ver.5で
書籍「実験!岩波データサイエンスvol.1」の4人のベイジアンによるベイズモデルを PyMC Ver.5で描いて分析します。
この書籍はベイズプログラミングのイロハをざっくりと学ぶことができる良書です。
楽しくPyMCモデルを動かして、ベイズと仲良しになれた気がします。
みなさんもぜひぜひPyMCで動かして、一緒に遊んで学びましょう!
4.楽しい写経 ベイズ・Python等
ベイズ、Python、その他の「書籍の写経活動」の成果をブログにします。
主にPythonへの翻訳に取り組んでいます。
写経に取り組むお仲間さんのサンプルコードになれば幸いです🍀
5.RとStanではじめる心理学のための時系列分析入門 を PythonとPyMC Ver.5 で
書籍「RとStanではじめる心理学のための時系列分析入門」の時系列分析をPythonとPyMC Ver.5 で実践します。
この書籍には時系列分析のテーマが盛りだくさん!
時系列分析の懐の深さを実感いたしました。
大好きなPythonで楽しく時系列分析を学びます。
6.データサイエンスっぽいことを綴る
統計、データ分析、AI、機械学習、Pythonのコラムを不定期に綴っています。
統計・データサイエンス書籍にまつわる記事が多いです。
「統計」「Python」「数学とPython」「R」のシリーズが生まれています。
7.Python機械学習プログラミング実践記
書籍「Python機械学習プログラミング PyTorch & scikit-learn編」を学んだときのさまざまな思いを記事にしました。
この書籍は、scikit-learnとPyTorchの教科書です。
よかったらぜひ、お試しくださいませ。
最後までお読みいただきまして、ありがとうございました。
