
「ウサギとカメ」の旅人算(開成中2023)
ウサギとカメが競走をしました。
カメはスタート地点からゴール地点まで、毎分4mの速さで走り続けました。
ウサギはスタート地点をカメと同時に出発し、毎分60mの速さで走っていましたが、ゴール地点まで残り100mになったところで走るのをやめて、昼寝を始めました。昼寝を始めた60分後に目を覚ましたウサギは、カメに追い抜かれていることに気がつきました。あわてたウサギは、そこから毎分80mの速さでゴール地点まで走りましたが、ウサギがゴール地点に着いたのは、カメがゴール地点に着いた時刻の5秒後でした。
次の問いに答えなさい。
⑴ウサギが昼寝を始めてからカメがゴール地点に着くまでの時間は何分何秒ですか。
⑵ウサギが昼寝を始めたとき、ウサギはカメより何m先にいましたか。
⑶スタート地点からゴール地点までの道のりは何mですか。
少し大げさに言えば、旅人算とは、複数の登場人物が、たがいに異なる速さで、ある道のりを動くときの、「速さ」「道のり」「時間」についてのドラマを追いかける問題です。そこで、旅人算を考えるときには、線分図を書くにせよ、ダイヤグラムを書くにせよ、物語文を読むときと同じように、時点ごとに場面分けをすることが肝心となります。
開成中によるこのフレッシュな問題は、「ウサギとカメ」という、私たちにとっておなじみの童話を旅人算の舞台とすることで、旅人算にそなわるドラマ性を実感できるものになっています。一見すると問題文が少し長めで、設定が複雑なようですが、誘導がとても親切なので、実はすっきりとシンプルに解き進めることができます。
最上位校の問題ですが、気後れせず、ぜひ、いろんな小学生に取り組んでもらいたい一題です。
(解)
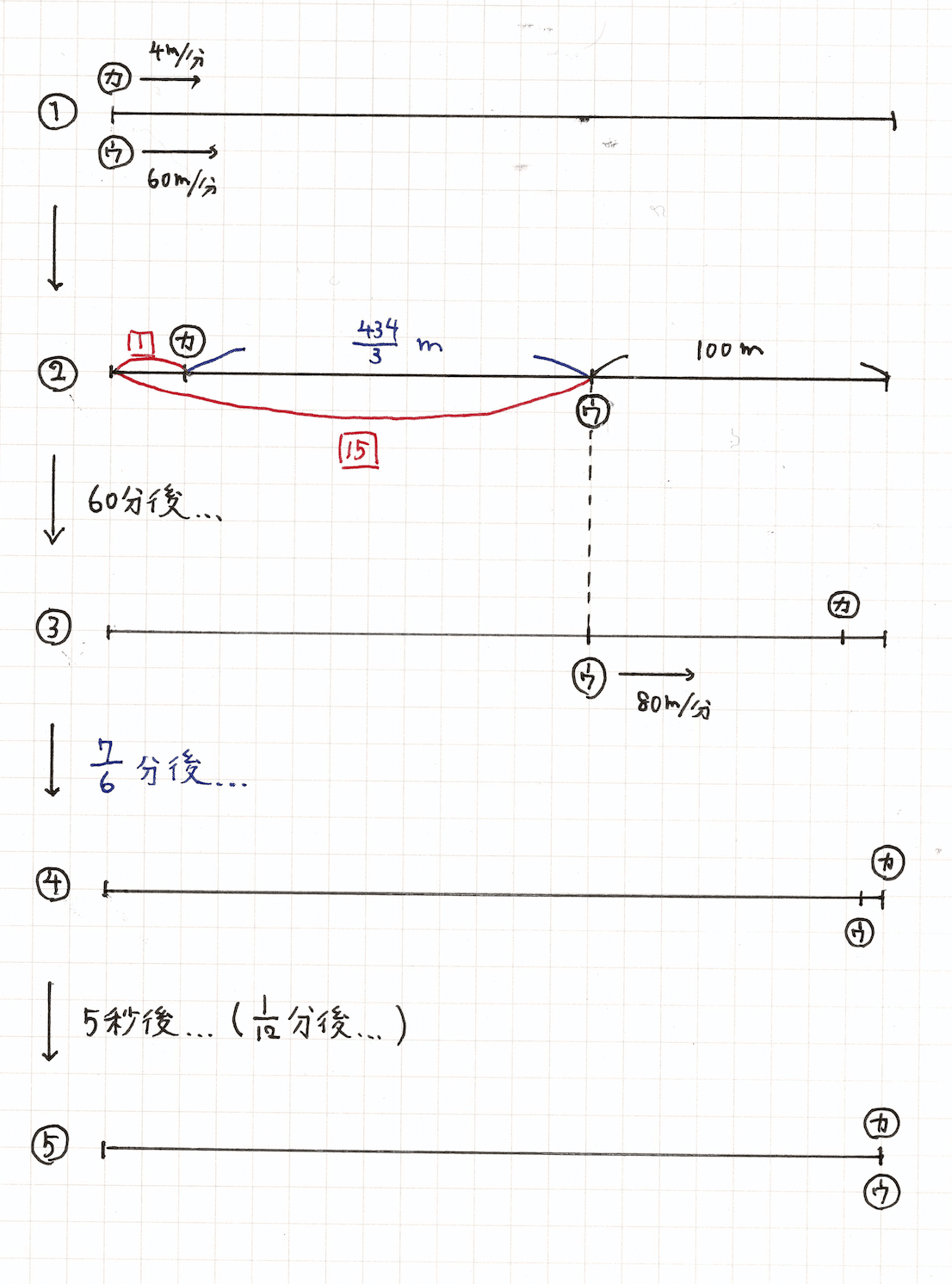
この問題は、次の5つの場面に分けられる。
①カメとウサギが同時にスタートした時点。
②ウサギが昼寝を始めた時点。
③ウサギが目覚めた時点。
④カメがゴールした時点。
⑤ウサギがゴールした時点。
⑴
③〜⑤までに、ウサギは毎分80mの速さで100mの道のりを走ったから、その間に経過した時間は
100÷80=5/4(分)
よって、③〜④までに、カメは5/4-1/12=7/6(分)走った。
したがって、②〜④までにカメは
60+7/6=61 1/6(分)
すなわち、61分10秒だけ走った。
⑵
すると、②で、カメのいる地点からゴール地点までの道のりは
4×61 1/6=734/3(m)
だから、このときのカメのいる地点からウサギのいる地点までの道のりは
734/3-100=434/3(m).
⑶
①〜②で、カメとウサギの進んだ道のりの比は、それぞれの速さの比の逆比に等しいので
4:60=1:15
よって、②でウサギのいる地点はスタート地点から
434/3×15/(15-1)=155(m)
したがって、スタート地点からゴール地点までの道のりは
155+100=255(m).(終)
ひとこと
この問題の解説として、ダイヤグラムを利用したものをよく見かけますが、個人的には、これは線分図にした方が、旅人算の「場面分け」の意味がわかりやすいと思ったので、今回は線分図を採用しています。意欲のある子は、ぜひダイヤグラムでも解いてみてください。
