されど食塩水（東大寺学園中2023）

　それぞれ一定の濃度の食塩水が出てくる3個のじゃ口A, B, Cを使って水そうに食塩水を入れます。A, B, Cからは毎分100gの食塩水が出ます。水そうは十分に大きいので食塩水があふれることはありません。また、水そうに入っている食塩水はすぐに混ざり合うものとして、次の問いに答えなさい。

⑴はじめ、水そうには濃度２%の食塩水が200g入っていて、全てのじゃ口は閉まっていました。まず、Aを３分間だけ開けて閉め、水そう内の食塩水の濃度を測定しました。ふたたび、Aを１分間だけ開けてから閉め、水そう内食塩水の濃度を測定したところ、さきほど測定したときよりも0.4%高くなっていました。Aから出てくる食塩水の濃度は何%ですか。

⑵ ⑴の後、AとBを同時に開け、２分後にBだけを閉めました。その後、水そう内の食塩水の濃度を複数回測定しても濃度が変わらなかったので、Aも閉めました。Bから出てくる食塩水の濃度は何%ですか。

⑶ ⑵の後、Cを４分間だけ開けてから閉め、水そう内の食塩水の濃度を測定すると３%高くなっていました。ふたたび、Cを４分間だけ開けてから閉め、水そう内の食塩水の濃度を測定するとさらに２%高くなっていました。Cから出てくる食塩水の濃度は何%ですか。

東大寺学園中（2023）

　食塩水の問題としてはかなり重厚です。決して生易しい問題ではありませんが、これまでに食塩水の問題を通して考えてきたことを総動員して、ぜひ勇気をもってチャレンジしてみてください。
　もし食塩水の基本（特に「比」「平均」との関係）の理解に自信がない子は、まずはこちらの問題に取り組んでみてください。

（解）
⑴

②→③の操作で水そうの食塩水の濃度が高くなったので、②で、Aの食塩水の濃度は水そうの食塩水の濃度より高い。
これより、面積図を描く。

アとイの長方形のタテの長さの比は100：500＝1：5だから、イのタテの長さは　　　
　　　0.4×5＝2（%）
よって、△＋2.4＝□がなりたつ。

　次に、①→②の操作について、面積図を描く。

ウとエの長方形のタテの長さの比は300：200＝3：2だから、ウのタテの長さは
　　　2.4×3/2＝3.6（%）
よって、△＝2+3.6＝5.6（%）だから、Aの食塩水の濃度（□）は、
　　　5.6+2.4＝8（%）．

⑵

⑴の後、AとBの食塩水を２分間水そうに入れ、その後Aの食塩水だけを入れ続けても水そうの食塩水の濃度が変化しなかったということは、AとBの食塩水を２分間入れた後の水そうの食塩水1000gの濃度が、Aと同じ８%であったことを意味する。
よって、200gのBの食塩水にふくまれる食塩の質量は、
　　　1000×8/100-(600×6/100+200×8/100)＝28（g）
である。
したがって、Bの食塩水の濃度は
　　　28÷200×100＝14（%）．

⑶ Cの食塩水を最初の４分間入れた後の面積図と、その後さらにCの食塩水を４分間入れた後の面積図をそれぞれ描く。

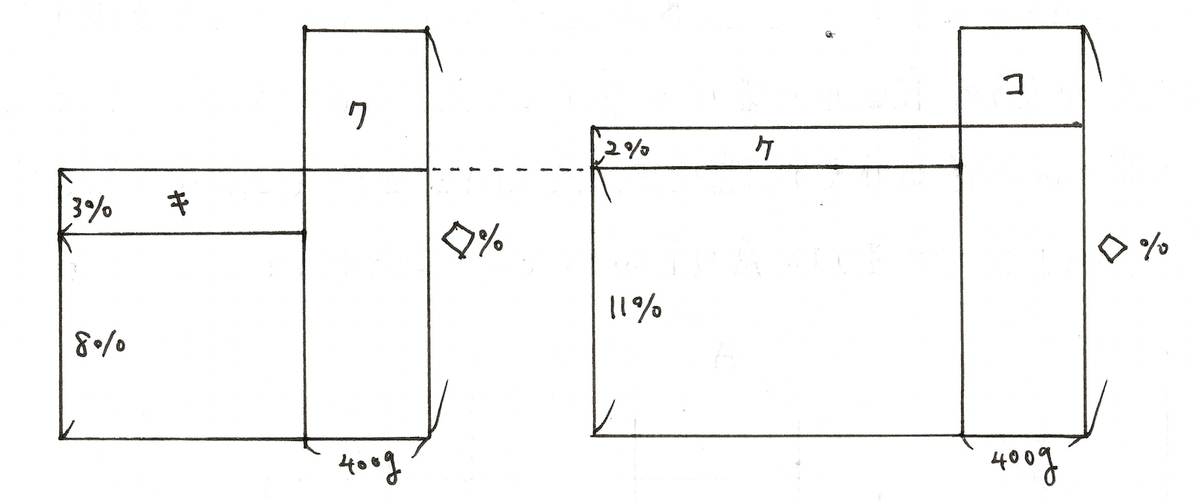
すると、キとク、ケとコの長方形の面積はそれぞれ等しい。
ここで、この２つの面積図を重ね合わせる。

図のように、各長方形にa, b, c, d, e, fと名づけると、
　　　キ＝a, ク＝c+e, ケ＝b+c, コ＝f
　　　（ただし、キ＝ク、ケ＝コ）
と表される。c=d, e=fだから、
　　　ク＝f+d
　　　　＝b+c+d
よって、aとb+c+dの面積は等しい。
この２つの長方形のタテの長さの比は3：2だから、ヨコの長さの比は2：3なので、aのヨコの長さは
　　　800×2/(3-2)＝1600（g）
すると、キとクのタテの長さの比は400：1600＝1：4だから、クのタテの長さは
　　　3×4＝12（%）
よって、Cの食塩水の濃度（◇）は
　　　◇＝11＋12＝23（%）．（終）

ひとこと

　食塩水の問題の基本的なアプローチは、「濃度と食塩水の質量から、ただちに食塩の質量を求めること」ですが、実際にはそれが難しい場合が多いです。そこで、そうした食塩水の問題を解くときに有効な主な道具として、面積図とてんびん図が挙げられます。今回は面積図の方を使って解きました。もちろん、てんびん図でも解けますが、てんびん図は、図そのものが食塩水の濃度の原理を説明してくれるわけではない、ということに注意が必要です。てんびん図はあくまで計算処理を簡単にするための「方便」に過ぎません。
一方、面積図は、
　　　（食塩の質量）＝（食塩水の濃度）×（食塩水の質量）
という関係を、長方形の面積の式
　　　（面積）＝（タテ）×（ヨコ）
に読みかえるという大胆な抽象化を前提とするものの、その関係を直接図化しているという点で、図そのものが食塩水の濃度の原理を説明できていると言えます。そのようなわけで、今回は面積図を採用し、パズルのように解ききってみました。
　てんびん図で考える場合は、てんびんの支点にさらにもう一つのてんびんを取り付けた「２重てんびん図」とでも呼べるようなものを描くことで、解くことができます。原理をしっかり理解している子は、ぜひてんびん図の方でもトライしてみてください。