
線形代数で検索結果を向上させるPageRank
線形代数を知っていれば,できることが圧倒的に増える.やりたいことができる可能性が高くなる.最高だ.
前回の記事はそう締めくくった.「研究とベンチャーと数学と」(その1,2,3)で,製造プロセス向けの異常検出技術を医療分野に転用することで,てんかん発作予知を実現したこと,その技術は線形代数を使ってこそ可能になったことを述べた.そんな記事を書いたのは,大学新入生が線形代数を勉強するモチベーションをあげるためだ.
折角なので,線形代数が威力を発揮した超有名な例を紹介しておこう.それは,GoogleのPageRankだ.
PageRankの発想
何かを調べたいときに,インターネットで検索すれば大概のことはわかる.実に素晴らしいことだが,小銭稼ぎが目的のゴミみたいなページが多いのも事実だ.ユーザは,良質なページを検索結果として表示することを検索サイトに求める.
では,どのようなページを検索結果の上位に表示すればいいのか.あるいは,どのようにしてページの重要度を決めればいいのか.
スタンフォード大学でコンピュータサイエンスを専攻する学生だったBrinとPageは,学術論文の重要度は被引用数(その論文を引用している論文の数)で評価されることに注目した.重要な論文は多くの論文から引用されて被引用数が多くなる.そうであれば,インターネットの世界でも,重要なページは多くのページからリンクされて被リンク数が多くなるはずだ.
しかし,単純に被リンク数が多いページを重要だと判断するわけにはいかない.そんなことをすれば,あるページAにリンクするゴミページを大量に作れば,ページAが重要だと判断されてしまう.このため,単純な被リンク数ではなく,多くの重要なページからリンクされているページが重要だと判断する.
また,ページBは1ページだけにリンクし,ページCは100ページにリンクしているとき,1つのリンクがもつ価値は同じではない.ページBからリンクされているページはとても重要そうだが,ページCからリンクされているページはどうでもよさそうに思える.そこで,あるページがリンクしているページの数も考慮して,リンクの価値を評価する.
まとめると,
1.被リンク数が多いページは重要である.
2.重要なページからのリンクは価値が高い.
3.リンク数が少ないページからのリンクは価値が高い.
という方針でページの重要度を決めればよい.こうして生み出されたのが,1998年に論文発表されたGoogle PageRankだ.Pageは,ウェブページのPageと,発明者の姓であるPageをかけている.

PageRankの計算
インターネットの世界に8つのページがあるとして,そのリンク関係を下図(How Google Finds Your Needle in the Web's Haystack, the American Mathematical Society)のような有向グラフであらわす.○はノードと呼ばれ,それぞれのページをあらわす.矢印はエッジと呼ばれ,リンクの向きをあらわす.
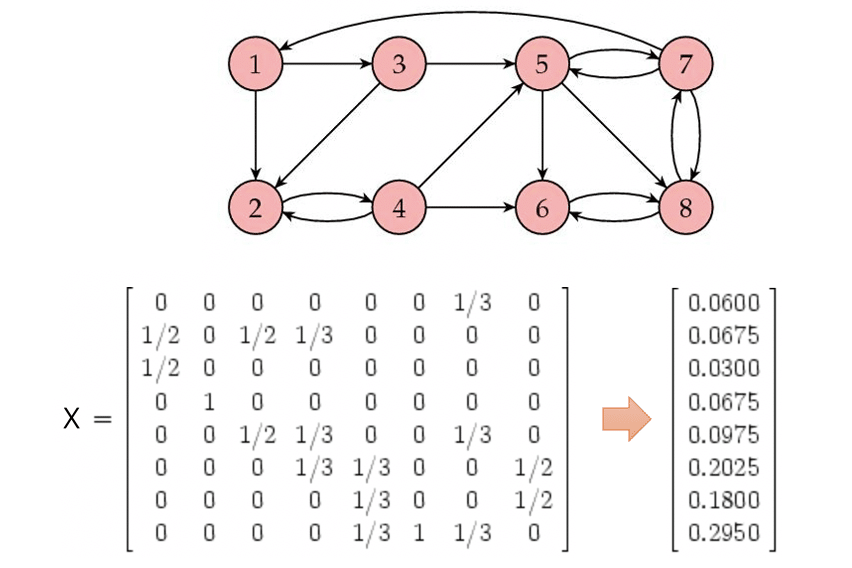
この有向グラフは隣接行列で表現できる.隣接行列の i 行 j 列要素は,ページ i からページ j へのリンクがあれば 1 ,なければ 0 とする.ただし,PageRankでは,あるページがリンクしているページの数でリンクの価値を評価するため,リンク数が k のとき,リンクの重みを 1 ではなく,1/k とする.この隣接行列の転置行列を X とする.
例えば,X において,ページ 3 はページ 2 と 5 にリンクしているので,3 行目の 2 列と 5 列の要素が 1/2 になっている.
・・・ 中略 ・・・
行列 X の最大固有値に対応する固有ベクトルを求めると,その固有ベクトルの各要素の値が,各ページの重要度,すなわちPageRankとなる.実に簡単だ.そう,線形代数を知っていればね.
行列・転置・固有値・固有ベクトル
前回の記事「研究とベンチャーと数学と(その3)」で次のように書いた.
線形代数以前の話かもしれないが,「行列」を知らないとどうしようもない.数字も知らないのに,足し算や掛け算はできない.それと同じで,行列を知らなければ,多次元空間で何もできない.
「特異値分解」「固有値分解」も線形代数に登場する方法だ.特に固有値分解は,主成分分析を含む多変量解析でいつも使われる道具であるため,データ解析を行うなら,どうしても理解しておく必要がある.
PageRankの計算で登場するのも,固有値と固有ベクトルだ.ある行列の最大固有値に対応する固有ベクトルを求めるという操作は,主成分分析(PCA)で主成分を求めるときの操作と同じである.
線形代数の威力が伝わっただろうか.まさに,いつでもどこでも線形代数だ.線形代数を知らないなんて,ちょっと話にならない.
講義が面白くなくても線形代数は重要
大切なので繰り返す.
大学新入生には是非とも「線形代数」を修得して欲しい.わかったような気になるだけでなく,使いこなせるほどに.線形代数を知っていれば,できることが圧倒的に増える.やりたいことができる可能性が高くなる.最高だ.
© 2020 Manabu KANO.
