
物理における左右の力の重要性
記事を見て頂きましてありがとうございます。
この記事では、物理に要求される左右の力(論理的、直感的処理能力)とその鍛え方について紹介していこうと思います。
記事の構成は次のようになっています。
まず導入として、物理に固有の特徴について説明します。
次に本論として、物理の理解に左右の力が重要であることを見ていきます。最後に展開として、左右の力の鍛え方の紹介と総括をして終わります。
また記事全体を通して、高校生向けの説明をしています。
それでは、よろしくお願いします。
導入~物理の特徴~
私は物理を専攻する大学院生です。
そんな私ですが、ここで一つ皆さんに聞いてみたいと思います。
あなたは物理についてどういう印象を持っていますか?
難しい?変わった人がやるもの?かっこいい?
いろいろな感想が出てくることでしょう。しかし私の見立てでは、ポジティブな意見はそこまで多くないのではないでしょうか。実際、私の周りにいる家族や友人のほとんどが、
「難しい、あんなもの分からない」
「物理をやる人は自分と頭の作りが根本的に違うから」
などと言います。私は、物理に特有のある特徴のせいで、人々がこういうイメージを持つのではないかと考えています。それは、
実際の現象を数式で表現する
というものです。
これは他の理系科目と決定的に違う点です。数学はもちろん数式を扱いますが、応用を考えない限りそれが直接身の回りの現象に結びつくことはありません。化学や生物、地学は実際の現象を扱いますが、それらを数式と結びつけることはそこまで多くありません。
この特徴が物理を大きく難化させ、理解できるものではないと多くの人々に印象付けてしまうのです。
本論~左右の力の重要性~
この物理特有の特徴をもう少し掘り下げてみると、物理で要求される能力は以下の2つであることが分かります。
(1)数式を処理し、解釈する能力(論理的処理能力)=左の力
(2)現象をイメージする能力(直感的処理能力) =右の力
(1)は数式の変形やその解釈といった、論理的処理能力です。(2)は(1)で行った解釈をイメージという形で実際の現象に当てはめる直感的処理能力です。脳では左脳と右脳がそれぞれ(1)、(2)を司ることから、私は(1)、(2)をそれぞれ左の力、右の力と呼んでいます。
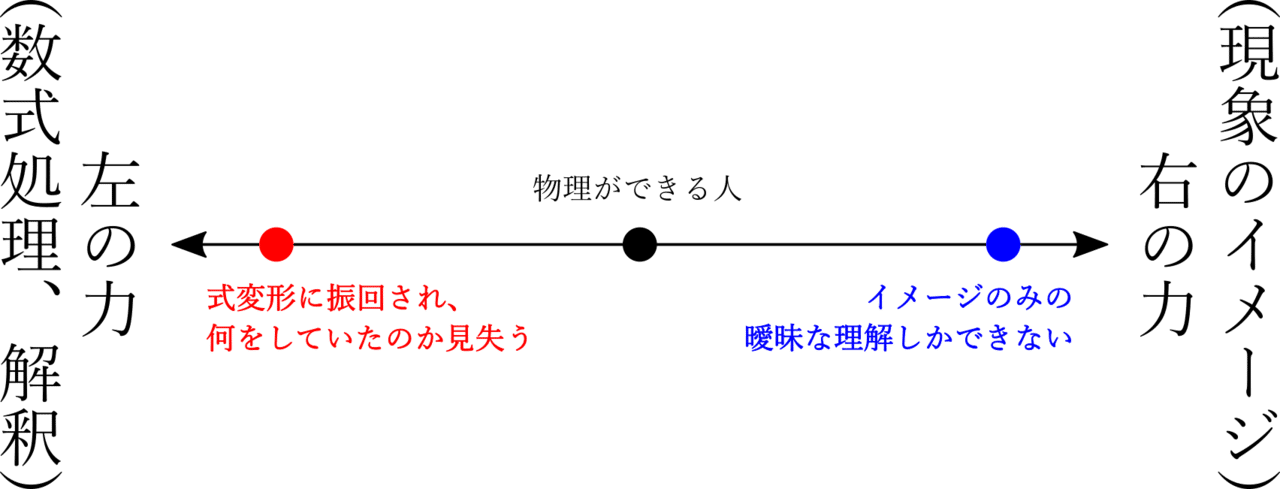
物理に苦手意識を抱く人は、力が左右のどちらかに大きく偏っていることが多いように感じます。例えば、上図の赤丸のような左に偏っている人は、直感的な理解をしない(できない)ために式変形に振り回され、答えを出したとしても自分が何をしていたのか分からなくなってしまいます。青丸のような右に偏っている人は、数式による物理の掘り下げをしない(できない)ために、イメージだけの曖昧な理解に終わってしまいます。
しかしそれも無理はありません。物理ほど左右の力を同時に使う機会が多くある理系科目は他にないですから。逆に言えば、左右の力をバランスよく使えるようになれば物理が得意になる可能性が高いというわけです。(※1)
私は物理が大好きです。数学という、物理とは全く独立に研究されていた学問がこんなにも現実をよく表せる。すごいことだと思いませんか?また数学が物理をよく表せるということは、逆に物理の知見から数学に発展をもたらす可能性もあるということです。(※2)そんな魅力と可能性に満ちた学問を、苦手意識から嫌いになってしまう人がいることをとても残念に思います。ですから私は、そういった人たちに左右の力を鍛えることで苦手意識を払拭し、物理を好きになってもらいたいのです。
展開~左右の力の鍛え方と総括~
では具体的にどう左右の力を鍛えていけばいいのでしょうか。
左と右、それぞれの力の鍛え方を以下で2つずつ紹介します。
左の力の鍛え方①:数学に対する理解を深める
物理に苦手意識を持つ人は、その原因が物理ではなく数学にあるのかもしれません。例えば、力学の運動方程式(F=ma)が分からないのは、文字式のルールを知らず、ma=m×aが分からないからかもしれません。作用・反作用の法則が分からないのは、正負の数に対する知識が足りないからかもしれません。数学が苦手な自覚のある人は、物理よりもまず数学の問題集をやるのがいいでしょう。その際には、自分に足りない数学の知識が何であるかを考えることが重要です。
左の力の鍛え方②:数式中の文字(数値)の意味を考える
また、数式自体に拒否反応を起こしてしまう人もいるかもしれません。そういう人は、数式中の文字(数値)が持つ意味を考えることから始めてみるといいでしょう。そうすることで文字と自分の持つイメージが結びつき、拒否反応が薄れるばかりでなく、数式全体を理解するための土台ができます。
少し練習をしてみましょう。
例えば力学で、自由落下する物体の速さvは時刻tの関数として

と表されます。まずは式中の文字の意味を考えるのでしたね。gは重力加速度の大きさを表します。つまり、地表で地球からの重力を受ける物体は1秒ごとにその速さがgずつ増えていくよ、ということを言っているのです。言い換えれば、重力加速度gに時刻tを掛け算すると時刻tにおける速さになります。これは式(*)が表すことに他なりません。このように、まずは式中の文字の意味を考えることから始めると、数式全体の表す意味が自ずと明らかになります。
また、次元解析も式の意味を考えるうえで強力な手段です。
次元とは、物理的な量を記述するときの基本的な単位の組み合わせのことで、これを見ることで文字や数式に対して解釈の引き出しを与えることができます。(※3)
式(*)を例にします。これは等式であるため、左辺と右辺は次元も一致しなければなりません。(速さ)=(道のり)÷(時間)であることから、左辺のvの次元は(長さ)÷(時間)です。一方、右辺の重力加速度gの次元は(速さ)÷(時間)=((長さ)÷(時間))÷(時間)=(長さ)÷(時間)^2です。これにtの次元(時間)を掛け算したものが右辺の次元なので、右辺の次元は(長さ)÷(時間)です。よって両辺の次元が一致していることを確かめられました。次元解析は数式の理解だけでなく、計算のチェックにも使えます。
右の力の鍛え方①:数式とイメージを対応させる癖をつける
先述したように、右の力を使わない人は式変形に没頭してしまい、答えを出しても自分が何をしていたのか分からなくなってしまいます。実は私も以前この状態に陥っていました。だからよく分かるのですが、こういう人は「この数式は何を表すのだろう…?」と考える習慣がないのです。式変形の沼に陥っている人は「数式が表す物事」を常に考えてみるとよいでしょう。そのときには、左の力の鍛え方②に書いたことも使えます。
右の力の鍛え方②:実験をする(見る)
現象のイメージがどうしてもできない(右の力を使えない)という人もいると思います。そういう人におすすめなのが「実験」です。実験は必ずしも自分で行う必要はありません。今は便利な時代で、様々な実験の動画がYouTubeをはじめとした動画サイトに多くアップロードされています。実験を行ったり見たりしていくうちに、少しずつ具体的なイメージの持ち方が分かっていくでしょう。そうして培ったイメージを式変形の最中に発揮してあげればよいのです。
総括
今回は、物理に要求される左右の力(論理的、直感的処理能力)とその鍛え方について紹介しました。この記事を読んで左右の力の鍛え方を実践し、一人でも多くの人が物理を好きになってくれることを願っています。
最後まで見て頂きまして、ありがとうございました。
脚注
(※1)見方を変えると、物理は論理的、直感的処理能力をバランスよく鍛えるのに最適な学問であると言えます。
(※2)実際、ペレルマンという人がポアンカレ予想という数学の難問を解くとき、物理的なアプローチを用いました。
(※3)例えば、熱力学で出てくるボルツマン定数は比熱と同じ次元を持っています。比熱とは、物質1g当たりの温度を1℃上げるのに必要なエネルギーでしたから、これを知っているとボルツマン定数が出てくる式の見え方が変わってきます。
今更の自己紹介
記事の最後で自己紹介する形になってしまい、申し訳ありません。
2回目ましてでした、ゆうはんと申します。
noteに投稿を始めたのは、文章を書く練習をしたかったからです。
ですので、もしよろしければ文章についてフィードバックを頂けると嬉しいです。
また、初投稿にスキして下さった7人の方々、本当にありがとうございます。書いた文章に対して反応を頂いてとても嬉しかったです。
今後ともよろしくお願いします。
