
10進数と2進数…数をどのように表現するか?2進小数について考える
はじめに
私たちは10進法で表記された数に囲まれて生活しているので、「2進数」と聞くとなんだか難しいな…と感じる方も多いのではないでしょうか。『2進数は神の数?』では、自然数の2進数について勉強しましたので、今回は小数について見てみましょう。実は古代エジプトでは、すでに2進小数に対応する概念を持っていたようです。もちろん現在の2進小数とまったく同じとまでは言えませんけれど。
「箱」でイメージしてみる
数という概念は簡単なようでとても難しいものです。まず10進数や2進数などの数の表現方法について復習しましょう。
日本では、大きな数を表すのに便利な記法を使用します。たとえば 304005060 は、三億四百万五千六十 と書き表すことができます。大きい数を扱う場合、単に数字を並べるよりこのように表記した方が数をとらえやすいと感じる方も多いと思います。今回は、漢数字の代わりに算用数字を使って 「 3億4百万5千6十 」のように表すことにします。ここで用いた「 億,万,千,百,十 」などを桁標識と呼びます。ソロバンをご存知の方は、各桁の上に桁標識が書かれたソロバンを思い浮かべてください。ソロバンになじみのない方は、図1 のように桁標識が付いた箱が並べられていると考えてください。一番右端の箱(最下位の箱)には桁標識がついていません。
各箱には 0 から 9 までの数字の一つが入ります。

たとえば 7, 6, 5, 4, 3, 2 がそれぞれの箱に入った場合、これが表す数値は
「 7十6万5千4百3 2 」となります。
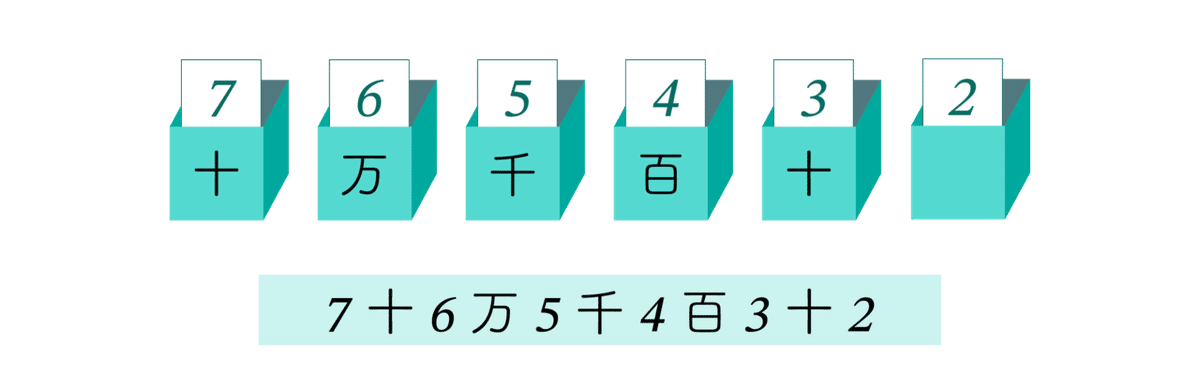
少し奇妙ですが、0 も省略せずに書くことにします。たとえば 十万 は
「 1十0万0千0百0十0 」
と表します。このように、10進数は「1から9までの数字を入れた箱が並んだもの」をイメージしてください。
次に2進数を考えてみましょう。図2のような箱を用意します。2進数の場合、箱に入る数字は 0 か 1 です。

それぞれの箱に 1、0、1、0、1を入れてみましょう。この2進数が表す数は以下のようになります。

1より小さい数を考える
1より小さい数、小数についても同じように考えることができます。中国では、次のような小さな数を表す単位を持っていました。
分 (ぶ), 厘 (りん), 毛 (もう) , 糸 (し), …
分は日本に入ってきてから「割」に変わりました。

図3 の箱の中には 0 から 9 の数が入ります。たとえば 13/16 は10進小数で 0.8125 ですから、小数点以下を順に箱に入れて、「 8割 1厘 2毛 5糸 」と読みます。

2進小数はどう表す?
2進小数も同様に考えてみましょう。2進小数の場合は、日本語には 1/4, 1/8, … に対する適当な名前も記号もありませんので、1/2¹, 1/2², 1/2³, 1/2⁴, 1/2⁵ と表すことにします。図4 のような桁標識がついた箱の列を想定します。

箱の中には 0 か 1 が入ります。13/16 を2進小数で表してみましょう。
13 = 8+4+1 なので、

となります。したがって、箱の中には左端から順に 1, 1, 0, 1 が入ります。右には無限に続く箱があり、 0 が入っているものと考えます。表示するときは、右側に 0. をつけ加え 0.1101 と書きます。これが2進小数です。

天秤で重さを量る
「2進数は神の数」では自然数の2進数の例として、100個の硬貨 ( 1円, 2円, 2²円 … )があれば世界中で扱われているどんな金額でも表せる、というお話をしました。小数の場合はどうでしょう。
古代では貨幣単位は、金とか銀の重さを表す重さでした。日本の円も明治になって両を言い換えたもので、両も金の重さを表すものでした。ここでは円の代わりに g (グラム) を使うことにします。最近は博物館にでも行かない限り天秤を見かけることはなくなりましたが、天秤では図のようにオモリを使って重さを量ります。天秤で使うオモリを分銅(ふんどう)といいます。以下のような分銅を持つ想像上の天秤を考えましょう。

ここで、「想像上の」といったのは、2の30乗分の1 グラムは約 0.1 ナノグラムという原子の重さより小さい重さになってしまうからです。こんなに小さいものは数学の世界以外には存在しません。
この天秤を使えば、1グラム以下のどんな重さでも量ることができるのです。以下の手順で重さを量ってみます。
図5のように天秤の右の皿に x グラムのものをおきます。最初に 1g の分銅を天秤の左の皿に起きます。釣り合ったら x = 1g です。天秤が右に傾いたら、x は 1g より重いのでこれ以上は量れません。

天秤が左に傾いた場合、つまり x が 1g より軽い場合を考えます( 図6 )。左の皿から1g の分銅を取り除き、 1/2g の分銅を載せます。天秤が左に傾くかどうかで、次のように判断できます。
左に傾いた場合、x は 1/2g より軽いことがわかります( 0 < x < 1/2 )。右に傾いた場合 x は 1/2g より重く1gより軽いことがわかります( 1/2 < x < 1 )。
右に傾いたとしましょう。左に 1/4g の分銅を追加します。左に傾いた場合はx は 1/2g より重く 3/4 より軽い( 1/2 < x < 3/4 )、右に傾いた場合は 3/4 gより重く 1g より軽い( 3/4 < x < 1 )ということになります。

この手順を繰り返し、天秤が釣り合ったところの分銅で x が量れたことになります。
使用した分銅の重さが 1/2g, 1/8g, 1/ 16g なら
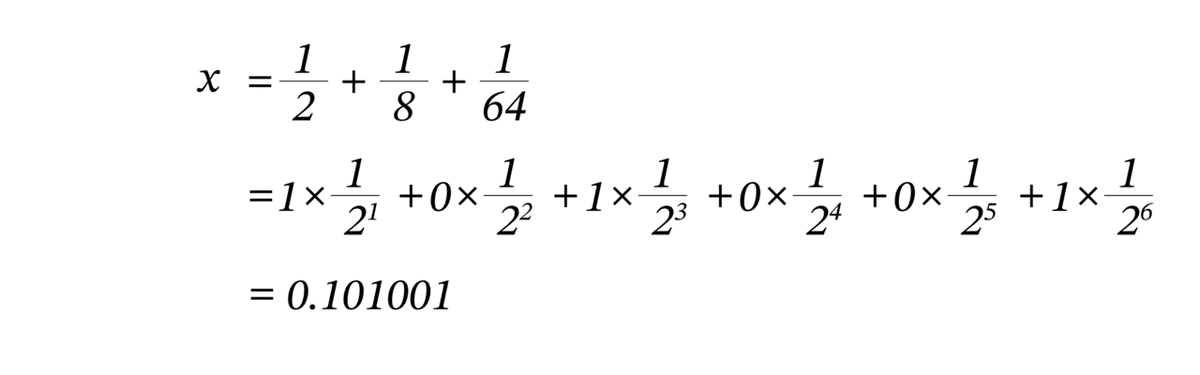
となります。
このように、この天秤と分銅を使えば 1グラム以下のどんな重さのものも量ることができます。現実世界では30番目の分銅まで使うことはありません。なにしろ30番目の分銅は原子の重さより小さいのですから。数学の世界では、とてつもなく大きな数や小さな数も、数式を使って簡単に表すことができます。また、数の表し方は一つだけではなく、時代や場所によっても様々なものがあり、私たちには馴染みのないものもたくさんあります。今回は数を表す「箱」や「天秤」を想像することで、数の表現方法について考えてみました。
![]()
▼関連記事
▼数学Webマガジン・マテマティカ 『ピラミッドの謎』
エジプトのピラミッドには多くの謎が隠されています。マテマティカのWeb連載『ピラミッドの謎』では、ピラミッドの数に関する3つの謎「円周率の謎」「黄金比の謎」「地球の緯度の謎」を取り上げます。古代エジプトの歴史やエジプト神話など、様々な角度からピラミッドの謎に迫ります!
noteの『古代エジプトの数学』シリーズで扱っている「古代エジプトの数学能力」を知ることが謎を解く鍵になります。ぜひ合わせてご覧ください。
![]()
▼Twitter、Webマガジンサイトも更新中。よろしくお願いいたします。
Twitter: @mathematicasite
Web:http://mathematica.site/


