TikZ 入門(3) ～点の名前をつける～

今回は、繰り返し使う点の名前をつける話です。

\coordinate を使ってみる！

図形の描画をするときは、同じ点から何本も辺を伸ばすことがあります。

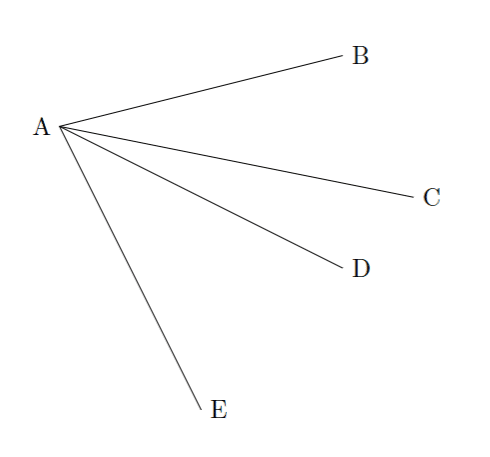
こんな感じでね。
これは

\begin{tikzpicture}[scale=1]

\draw (-1,2) node[left]{A} -- (3,3) node[right]{B};
\draw (-1,2) -- (4,1) node[right]{C};
\draw (-1,2) -- (3,0) node[right]{D};
\draw (-1,2) -- (1,-2) node[right]{E};

\end{tikzpicture}

と入力しました。
で、出力してみたら「ちょっとバランスが違う」と感じて、点 A の位置を微妙に変えたいとすると、上のコードの (-1,2) をすべて書き変えなきゃいけないのでメンドウです。

このように何度も同じ点を使うときには、 \coordinate が便利です。これは
　　\coordinate (点の名前) at (座標);
と書くことで、点（座標）の名前を（点の名前）とするコマンドです。
これを利用して

\coordinate (A) at (-1,2);
\draw (A) -- (3,3) node[right]{B};
\draw (A) -- (4,1) node[right]{C};
\draw (A) -- (3,0) node[right]{D};
\draw (A) -- (1,-2) node[right]{E};

とすると

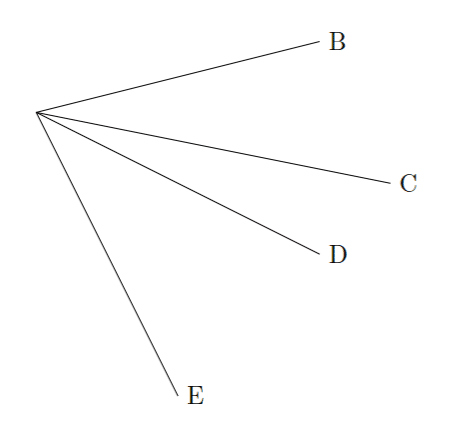
と、ほぼ同じものが出力されます。
ついでに、点 A のラベルをつけるには
　　\coordinate (A) at (-1,2);
を
　　\coordinate[label=left:A] (A) at (-1,2);
としてあげれば

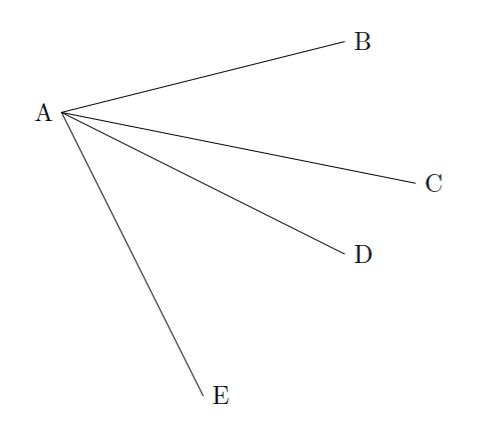
となります。

こうしておくと、例えば点 A の位置を (0,0) に変更したければ

\coordinate[label=left:A] (A) at (0,0);
\draw (A) -- (3,3) node[right]{B};
\draw (A) -- (4,1) node[right]{C};
\draw (A) -- (3,0) node[right]{D};
\draw (A) -- (1,-2) node[right]{E};

とするだけで

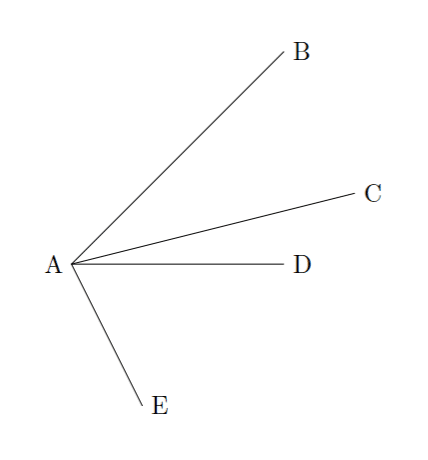
と出力されます。

\coordinate[label=left:A] (A) at (-3,-1);
\draw (A) -- (3,3) node[right]{B};
\draw (A) -- (4,1) node[right]{C};
\draw (A) -- (3,0) node[right]{D};
\draw (A) -- (1,-2) node[right]{E};

とすれば

となります。

なので、純粋幾何の図形を描画するときは最初に各点の名前を \coordinate しておくのがオススメです♪

正多角形を描く

TikZ の座標は計算をしてくれるので、正多角形を描くときは、三角関数を利用して座標を入力するのが便利です。
正五角形なら、単位円上の π/2 の点 (0,1) から始めて 2π/5 ずつ回転した点をとれば良いわけです。なので

\begin{tikzpicture}[scale=2]

\coordinate (A) at (0,1);
\coordinate (B) at ({cos(9*pi/10 r)},{sin(9*pi/10 r)});
\coordinate (C) at ({cos(13*pi/10 r)},{sin(13*pi/10 r)});
\coordinate (D) at ({cos(17*pi/10 r)},{sin(17*pi/10 r)});
\coordinate (E) at ({cos(21*pi/10 r)},{sin(21*pi/10 r)});

\draw (A)--(B)--(C)--(D)--(E)--cycle;

\end{tikzpicture}

とすれば

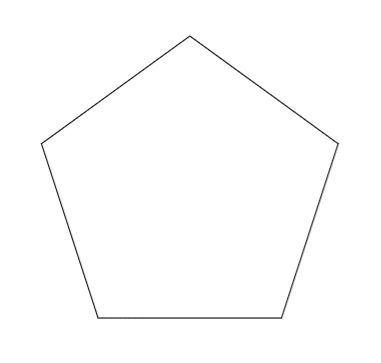
と出力されます。
そして、\coordinate コマンドを使っているので、対角線を引きたいときは
　　\draw[very thin,dashed] (A)--(C)--(E)--(B)--(D)--cycle;
とでも付け加えれば

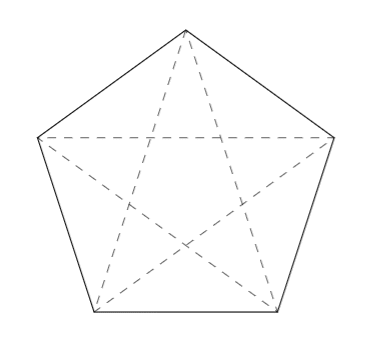
となります。

繰り返し処理の \foreach

TikZ では同じ処理の繰り返しをしてくれるコマンド \foreach があります。
　　\foreach \変数 in{変数の動く集合} 命令
と入力すると、命令を \変数 が動く分だけ繰り返してくれます。例えば

\foreach \k in{1,...,5}
    \coordinate (A_\k) at ({cos((4*\k+1)*pi/10 r)},{sin((4*\k+1)*pi/10 r)});

とすると、点 A_1 から A_5 を定めてくれます。そして

\draw[red,very thick] (A_1)--(A_2)--(A_3)--(A_4)--(A_5)--cycle;
\draw[blue,very thin] (A_1)--(A_3)--(A_5)--(A_2)--(A_4)--cycle;

とすると

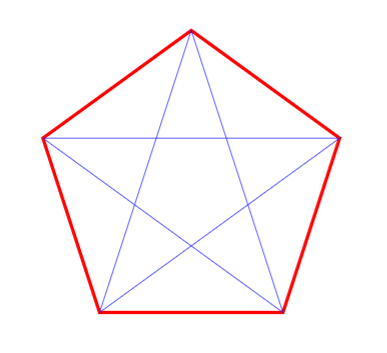
と出力されます。さらに

\foreach \k in{1,...,5} \draw ($(0,0)!1.15!(A_\k)$) node{$\mathrm{A_\k}$};

と付け加えると

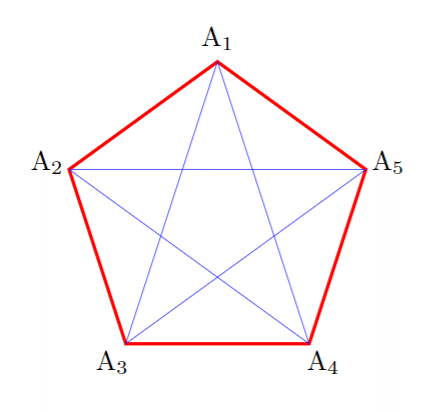
となります。
($(0,0)!1.15!(A_\k)$) は、点 (0,0) から点 (A_\k) の方向に 1.15 進んだ点を表しています。そこに node{$\mathrm{A_\k}$} で、A_\k と書くことを \k=1,...,5 と繰り返すように命令しています。

今回は \coordinate と \foreach の基本的な使い方についてのお話でした。