
TikZ 実用例(11)~\tikzmath~
またまた久しぶりの投稿です(すみません…)。
今回は \tikzmath を紹介します。(今までにも使った例を出してはいますが)
図中で計算させる!
\tikzmath を使うと、変数を設定できます。(という認識なのですがあってます?)
例えば
\begin{tikzpicture}
\tikzmath{
\a = 3;
\b = 2;
}
\draw (0,0) node {$\a$}
(1,0) node {$\b$}
;
\end{tikzpicture}とすると
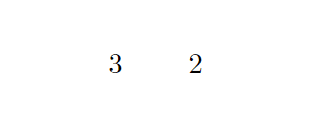
と出力されます。
これは、\tikzmath の中で、\a を 3、\b を 2 と定義して、座標 (0, 0) に \a、(1, 0) に \b を出力しているということです。
もちろん、これだけなら \tikzmath を使う必要はありません。
次に、座標 (2, 0) に和 \a+\b の値を出力したいと思います。
例えば
\begin{tikzpicture}
\tikzmath{
\a = 3;
\b = 2;
}
\draw (0,0) node {$\a$}
(1,0) node {$\b$}
(2,0) node {$\a+\b$}
;
\end{tikzpicture}としても
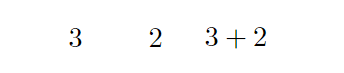
となるだけで、和の値は計算されません。
ただ \a+\b と出力するだけになってしまいます。
そこで
\begin{tikzpicture}
\tikzmath{
\a = 3;
\b = 2;
int \s;
\s = \a+\b;
}
\draw (0,0) node {$\a$}
(1,0) node {$\b$}
(2,0) node {$\s$}
;
\end{tikzpicture}とすると
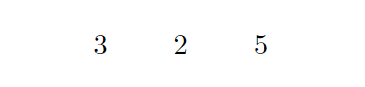
となって,和が計算されて「5」と出力されます!
これは
int \s; で「整数値の変数 \s」を用意しておき、
\s = \a+\b; でその \s を \a+\b の計算結果と定義している
ということです。
サイコロ2個の36マス
自分は『場合の数・確率』の基本は「数え上げ!」と教えています。
だから、樹形図や表を多用して説明するのです。
そうすると、「サイコロ2個」の問題で36マスの表を描くことが多いわけです。
例えば
「2個のサイコロを投げるとき、目の和が3の倍数となる確率は?」
なんて問題に対する解答として、自分は36マスを描いて和の値を書き込みたいのです。
それがこれ!
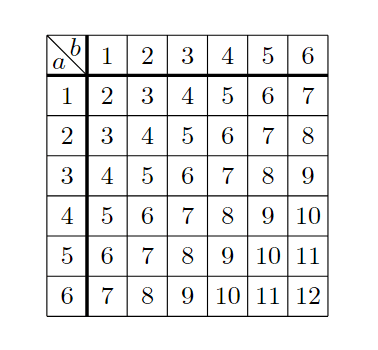
これを数えて、答えは 12/36 = 1/3 です。
まぁ、これぐらいなら他の方法でも効率よく答えを得られますが、今はそんなことはどーでもよくて、とにかく「36マスの表」を描きたいのです!
これは
\begin{tikzpicture}[scale=0.5]
\draw (-1,1) grid[step=1] (6,-6)
(-1,1)--(0,0)
(-0.7,0.3) node {$a$}
(-0.3,0.7) node {$b$}
;
\draw[very thick] (0,1)--(0,-6) (-1,0)--(6,0);
\foreach \a in{1,...,6}{
\draw (-0.5,-\a+0.5) node {$\a$}
(\a-0.5,0.5) node {$\a$}
;
\foreach \b in{1,...,6}{
\tikzmath{
int \s;
\s = \a+\b;
}
\draw (\b-0.5,-\a+0.5) node {$\s$};
}
}
\end{tikzpicture}と入力しています。
解説
どういうことかというと、まず
\draw (-1,1) grid[step=1] (6,-6)
(-1,1)--(0,0)
(-0.7,0.3) node {$a$}
(-0.3,0.7) node {$b$}
;
\draw[very thick] (0,1)--(0,-6) (-1,0)--(6,0);で、次図のように格子状の線(プラスα)を描いています。
(位置を分かりやすくする為に、赤い座標軸を入れてあります)
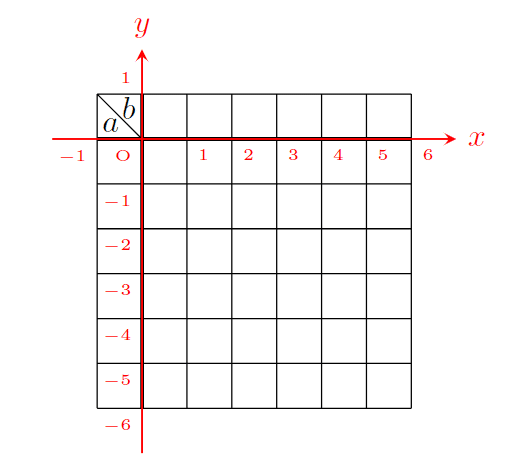
そして、\foreach で \a を1、2、…、6まで動かしながら
\foreach \a in{1,...,6}{
\draw (-0.5,-\a+0.5) node {$\a$}
(\a-0.5,0.5) node {$\a$}
;
}とすると
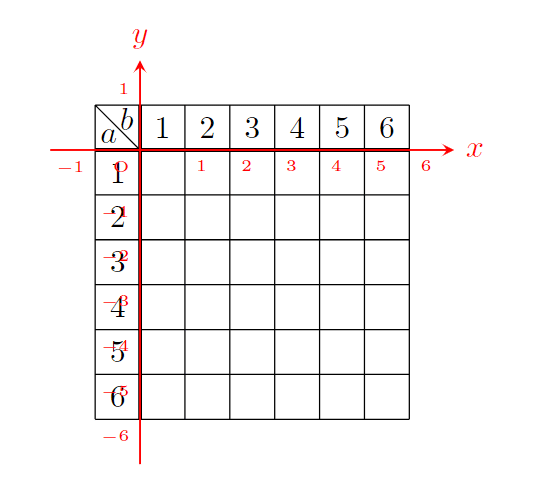
となります。
つまり、座標 (-0.5, -\a+0.5) と (\a-0.5, 0.5) に \a の値を出力しています。
そして、この \foreach の中で、さらに \foreach を重ねて \b を1から6まで動かすのですが、まずは \b = 1 で固定した場合を見てみましょう。
\foreach \a in{1,...,6}{
\draw (-0.5,-\a+0.5) node {$\a$}
(\a-0.5,0.5) node {$\a$}
;
\foreach \b in{1}{
\tikzmath{
int \s;
\s = \a+\b;
}
\draw (\b-0.5,-\a+0.5)node{$\s$};
}
}このようにすると、座標 (1-0.5, -\a+0.5) に和 \s = \a+1 の値を出力して

となります。
したがって、\b を1から6まで動かして
\foreach \a in{1,...,6}{
\draw (-0.5,-\a+0.5) node {$\a$}
(\a-0.5,0.5) node {$\a$}
;
\foreach \b in{1,...,6}{
\tikzmath{
int \s;
\s = \a+\b;
}
\draw (\b-0.5,-\a+0.5)node{$\s$};
}
}とすると
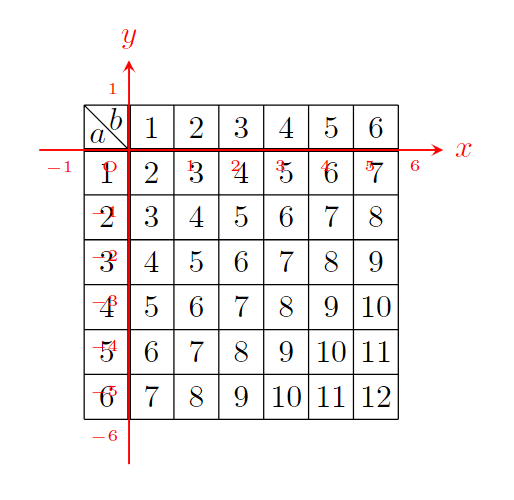
となります♪
和以外の例
したがって、\s の定義をいじることで、違うパターンの36マスも作れるわけです。
例えば
\begin{tikzpicture}[scale=0.5]
\draw (-1,1) grid[step=1] (6,-6)
(-1,1)--(0,0)
(-0.7,0.3) node {$a$}
(-0.3,0.7) node {$b$}
;
\draw[very thick] (0,1)--(0,-6) (-1,0)--(6,0);
\foreach \a in{1,...,6}{
\draw (-0.5,-\a+0.5) node {$\a$}
(\a-0.5,0.5) node {$\a$}
;
\foreach \b in{1,...,6}{
\tikzmath{
int \s;
\s = \a*\b; %%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 変更箇所はここだけ
}
\draw (\b-0.5,-\a+0.5) node {$\s$};
}
}
\end{tikzpicture}とすれば、積 \s = \a*\b の値を出力して
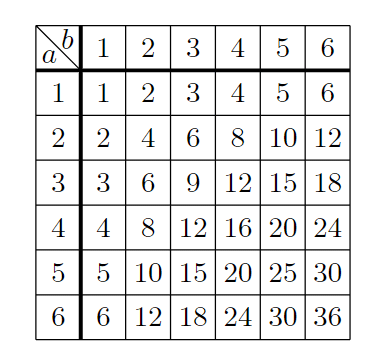
となるし
\begin{tikzpicture}[scale=0.5]
\draw (-1,1) grid[step=1] (6,-6)
(-1,1)--(0,0)
(-0.7,0.3) node {$a$}
(-0.3,0.7) node {$b$}
;
\draw[very thick] (0,1)--(0,-6) (-1,0)--(6,0);
\foreach \a in{1,...,6}{
\draw (-0.5,-\a+0.5) node {$\a$}
(\a-0.5,0.5) node {$\a$}
;
\foreach \b in{1,...,6}{
\tikzmath{
int \s;
\s = mod(\a*\b,4); %%%%%%%%%%%%%%%%%%%%%%%%%%%%%% 変更箇所はここだけ
}
\draw (\b-0.5,-\a+0.5) node {$\s$};
}
}
\end{tikzpicture}とすれば、積 \a*\b を4で割った余りを出力して
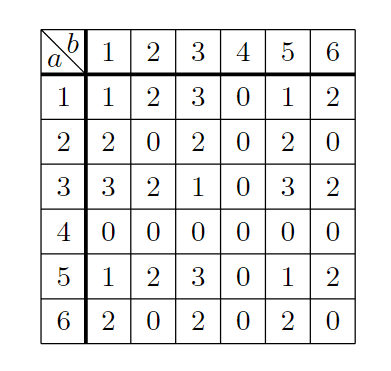
となります。
(ちなみに、これは 2013 年の北海道大(理系)前期の問題)
以前の記事でも、三角形の外接円や内接円のときに \tikzmath を使っているので、ご参考にしていただければ幸いです。
それでは、また、いつの日か!
この記事が気に入ったらサポートをしてみませんか?
