
TikZ 実用例(10)~繰り返し処理~
久しぶりの投稿です。
長い間、待たせてゴメン…(Kiroro って、今何してるの?)
今回は、繰り返し処理の \foreach を解説します。(以前の記事にも出てますが…)
基本的な使い方
基本的には
\foreach 変数 in{変数の動く集合} 命令
という形で使います。
例えば
\foreach \x in{1,2,3,4,5} \draw (\x,0) node{ほげ};とすると
となります。
これは、変数 \x を 1 から 5 まで動かして、点 (\x, 0) に「ほげ」と書いています。
なお、これは
\foreach \x in{1,...,5} \draw (\x,0) node{ほげ};としても、同じように出力してくれます。
「命令」を { } 内に入れて、複数の命令を実行することもできます。
例えば
\foreach \x in{1,...,5}
{
\draw (\x,0) node{ほげ};
\draw[->,>=latex] (\x,0.3) to[bend left=30] (\x+0.9,0.3);
};とすると

となります。
変数のとり方
変数の動く範囲の集合の「…」はけっこう賢くて
\draw[step=1,very thin,gray] (0,0) grid (10.5,10.5);
\draw[->,>=stealth,semithick] (0,0)--(10.5,0) node[right]{$x$};
\draw[->,>=stealth,semithick] (0,0)--(0,10.5) node[above]{$y$};
\draw (0,0) node[below left]{O};
\foreach \n in{2,4,...,10}
{
\draw (\n,0) node[below]{\small $\n$}
(0,\n) node[left]{\small $\n$}
;
};とすると、「偶数だけだな」と解釈してくれて

としてくれます。
また、変数は数でなくても構いません!
例えば、次のように「点の名前」をとることもできます。
\draw[step=1,very thin,gray] (0,0) grid (10.5,10.5);
\draw[->,>=stealth,semithick] (0,0)--(10.5,0) node[right]{$x$};
\draw[->,>=stealth,semithick] (0,0)--(0,10.5) node[above]{$y$};
\draw (0,0) node[below left]{O};
\foreach \n in{2,4,...,10}
{
\draw (\n,0) node[below]{\small $\n$}
(0,\n) node[left]{\small $\n$}
;
};
%%% ここまでは1つ前の例と同じ %%%
\coordinate (A) at (2,1);
\coordinate (B) at (3,8);
\coordinate (C) at (5,2);
\coordinate (D) at (7,3);
\coordinate (E) at (8,1);
\foreach \P in{A,...,E}
{
\fill[red] (\P) circle[radius=3pt];
\draw[red] (\P) node[above]{\P};
};
とすると
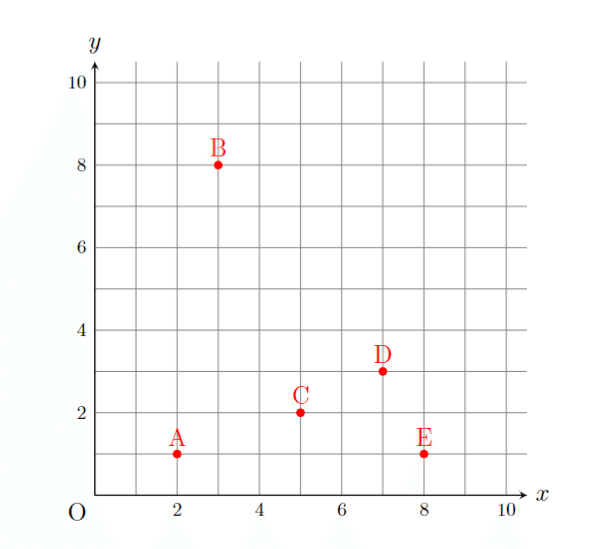
となります。
2変数の場合
変数を2つ設定したい場合には
\foreach \x/\y in{集合} 命令
という形で入力します。
つまり,組 (\x, \y) を \x/\y と表現しているようです。
だから、例えば
\draw[step=1,very thin,gray] (0,0) grid (10.5,10.5);
\draw[->,>=stealth,semithick] (0,0)--(10.5,0) node[right]{$x$};
\draw[->,>=stealth,semithick] (0,0)--(0,10.5) node[above]{$y$};
\draw (0,0) node[below left]{O};
\foreach \n in{2,4,...,10}
{
\draw (\n,0) node[below]{\small $\n$}
(0,\n) node[left]{\small $\n$}
;
};
%%% ここまで上の例と同じ %%%
\foreach \x/\y in{2/1,3/8,5/2,7/3,8/1} \fill (\x,\y) circle[radius=3pt];とすることで,点 (\x, \y) を一気にプロットできて、次図のようになります。
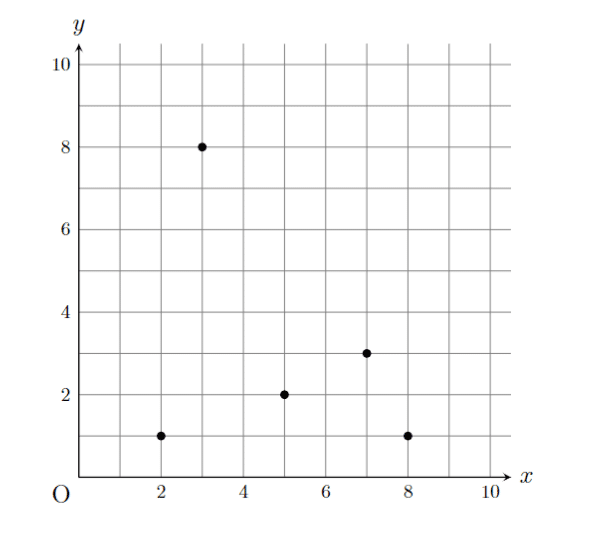
ちなみに \foreach を重ねて
\draw[step=1,very thin,gray] (0,0) grid (10.5,10.5);
\draw[->,>=stealth,semithick] (0,0)--(10.5,0) node[right]{$x$};
\draw[->,>=stealth,semithick] (0,0)--(0,10.5) node[above]{$y$};
\draw (0,0) node[below left]{O};
\foreach \n in{2,4,...,10}
{
\draw (\n,0) node[below]{\small $\n$}
(0,\n) node[left]{\small $\n$}
;
};
%%% ここまで上の例と同じ %%%
\foreach \x in{1,...,10}
\foreach \y in{1,...,10} \fill (\x,\y) circle[radius=3pt];とすると
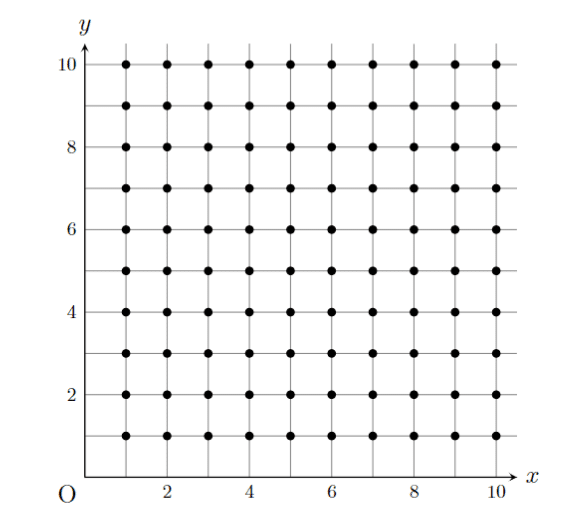
となります。
区分求積法の図
この \foreach を利用して、区分求積法の図を描いてみました。

ソースコードはこちら。
\begin{tikzpicture}[scale=3,samples=100]
\foreach \k in{0.1,0.2,...,0.9,1.0}
\filldraw[fill=black!20!] (\k-0.1,0) rectangle (\k,{pow(\k,2)});
\draw[->,>=stealth,semithick] (-0.2,0)--(1.2,0) node[right]{$x$};
\draw[->,>=stealth,semithick] (0,-0.2)--(0,1.5) node[left]{$y$};
\draw (0,0) node[below left]{O}
(1,0) node[below]{$1$}
(0.6,0) node[below]{\footnotesize$\bunsu{k}{n}$}
;
\draw[dashed,very thin] (0.5,0.36)--(0,0.36)
node[left]{\footnotesize$\left(\bunsu{k}{n}\right)^{\hspace{-2pt}2}$};
\draw[very thick] plot[domain=-0.2:1.2] (\x,{pow(\x,2)}) node[above]{$y=x^2$};
\end{tikzpicture}折れ線グラフ
「統計」の授業で使えそうな「折れ線グラフ」はこんな感じ。

ソースコードはこちら。
\begin{tikzpicture}[scale=1]
\draw[step=1,very thin, gray] (0,0) grid (5.5,5.5);
\draw[->,>=stealth,semithick] (0,0)--(5.5,0) node[right]{$x$};
\draw[->,>=stealth,semithick] (0,0)--(0,5.5) node[above]{$y$};
\draw (0,0) node[below left]{O};
\foreach \x/\y in{0/2,1/3,2/0,3/4,4/1,5/2}
{
\coordinate (P{\x}) at (\x,\y);
\fill (P{\x}) circle[radius=2pt];
}
\foreach \x in{1,...,5}
{
\small
\draw (\x,0) node[below]{$\x$}
(0,\x) node[left]{$\x$}
;
}
\foreach \m in{0,...,4}
{
\tikzmath
{
int \n;
\n=\m+1;
}
\draw[very thick] (P{\m})--(P{\n});
}
\end{tikzpicture}最後の方の \tikzmath で「変数 \n を \m+1 で定義」して使うことが出来たとき、自分はとても気持ちよかったです(笑)
今回はここまで。参考になったでしょうか?
それでは、また、そのうちお会いしましょう!
この記事が気に入ったらサポートをしてみませんか?
