TikZ 入門(2) ～関数グラフを描く～

我々の仕事（数学を教える仕事）で一番多く描くのは関数グラフです。（中学生相手だと幾何の方が多いかも…）
そこで、今回は y=f(x) 型の関数グラフの描き方を説明します。

座標軸

前回（TikZ 入門(1)）の要領で、まずは座標軸を描きましょう。
文章中に

\begin{tikzpicture}[scale=1]

\draw[->,>=stealth,semithick] (-3,0)--(3,0) node[right]{$x$}; %x軸
\draw[->,>=stealth,semithick] (0,-1)--(0,4) node[left]{$y$}; %y軸
\draw (0,0) node[below left]{O}; %原点

\end{tikzpicture}

と書きます。もちろん、座標軸の範囲は好きなように設定してください。
で、コンパイルすると

こんな感じ。

関数グラフの入力

さて、本題ですが、y=f(x) 型のグラフを描かせるには「plot」というコマンドを使います。例えば、y=x/2+1 のグラフは

\draw plot(\x,\x/2+1);

と入力してあげれば

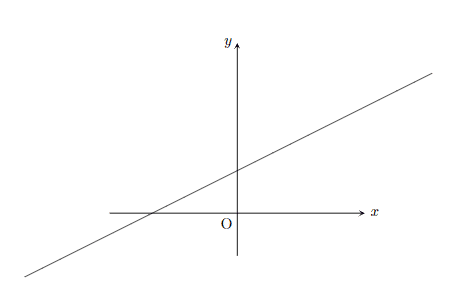
となります。
x 座標 \x に対して、y 座標を \x の式で表現してあげるということですね。
このとき
　四則演算　+ - * /
　べき関数 x^n　pow(\x,n)
　ルート √x　sqrt(\x)
　三角関数　sin(\x),   cos(\x),   tan(\x)　（度数法）
　三角関数　sin(\x r),   cos(\x r),   tan(\x r)　（弧度法）
　指数関数　exp(\x)
　対数関数　ln(\x)，log2(\x)
などが使えます。（plot 以外でも使えます。）

太さを変えたり、定義域を指定するときは

\draw[thick,domain=-3:3] plot(\x,\x/2+1);

というオプションをつけてあげます。そうすると

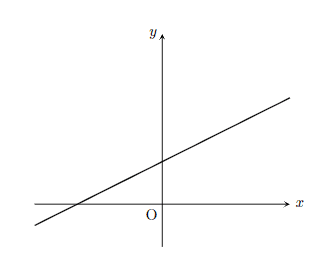
となります。

滑らかな曲線を描く

plot という名前の通り、点をいくつかプロットして結んでいるようです。
だから、曲線を描くとカクカクします。例えば

\draw[->,>=stealth,semithick] (-4,0)--(4,0) node[right]{$x$}; %x軸
\draw[->,>=stealth,semithick] (0,-3)--(0,3) node[left]{$y$}; %y軸
\draw (0,0) node[below left]{O}; %原点
\draw[thick,domain=-4:4] plot(\x,{2*sin(\x r)});

とすると

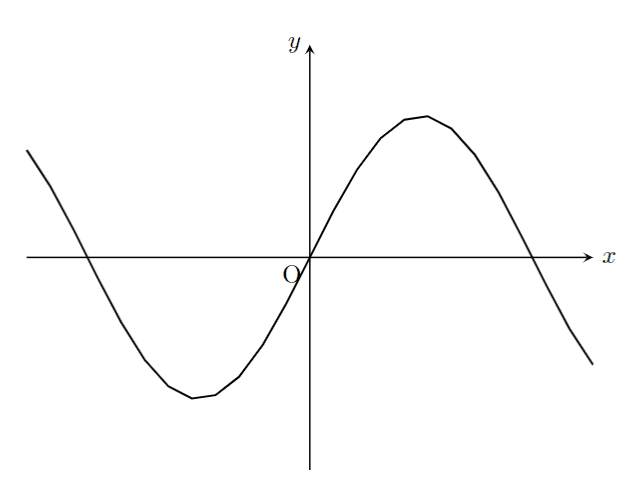
こんな感じ。

この plot する点を増やしてあげれば滑らかに繋がるはずです。そこで
\begin{tikzpicture}[scale=1]
のオプションを

\begin{tikzpicture}[scale=1,samples=300]

としてあげます。そうすると

イイ感じ♪

図を切り取る

いくつかのグラフをひとつの座標平面に描くときは、ひとつひとつの定義域を考えるのが面倒です。雑に

\draw[->,>=stealth,semithick] (-4,0)--(4,0) node[right]{$x$}; %x軸
\draw[->,>=stealth,semithick] (0,-3)--(0,3) node[left]{$y$}; %y軸
\draw (0,0) node[below left]{O}; %原点
\draw[thick,domain=-4:4] plot(\x,{sin(\x r)});
\draw[thick,domain=-2:2] plot(\x,{pow(\x,2)});
\draw[thick,domain=-4:4] plot(\x,\x);

なんて入力すると

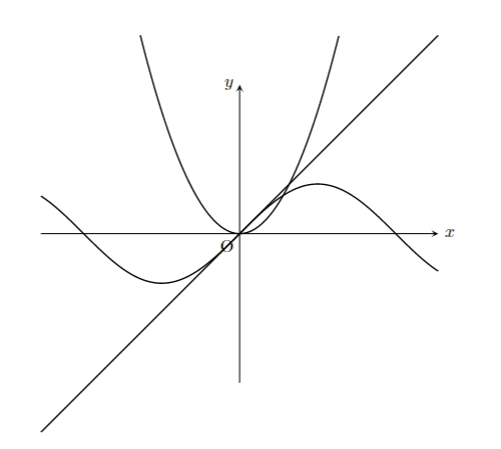
こんな感じ。
つまり domain というのは x の範囲の指定だけなので、y の範囲指定ができないのです。
そこで scope 環境の \clip というコマンドが便利です。

\begin{scope} \clip (左下) rectangle (右上);
グラフの入力
\end{scope}

とすると (左下) から (右上) までの長方形の範囲を切り取って、そこだけ描画してくれるのです。このとき、各グラフの domain 指定は不要です。
例えば

\draw[->,>=stealth,semithick] (-4,0)--(4,0) node[right]{$x$}; %x軸
\draw[->,>=stealth,semithick] (0,-3)--(0,3) node[left]{$y$}; %y軸
\draw (0,0) node[below left]{O}; %原点
\begin{scope} \clip (-4,-3) rectangle (4,3);
  \draw[thick] plot(\x,{sin(\x r)});
  \draw[thick] plot(\x,{pow(\x,2)});
  \draw[thick] plot(\x,\x);
\end{scope}

とすると

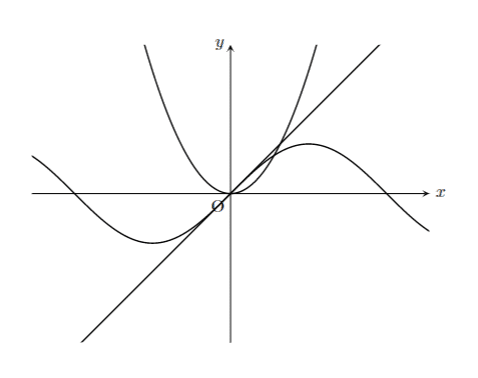
こんな感じ。
ついでに、\end{scope} の下に

\draw ({-sqrt(3)},3) node[above]{$y=x^2$};
\draw (3,3) node[right]{$y=x$};
\draw (4,{sin(4 r)}) node[below]{$y=\sin x$};

とでも入力すれば

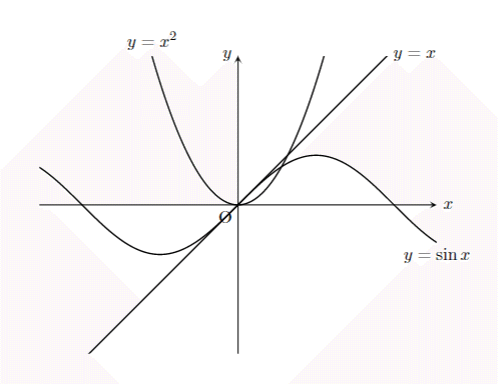
こんな感じになります。
座標軸や、各グラフの式などは scope 環境の外に書かないと、切り取られてしまい描画されない可能性がありますので注意が必要です。

今回はここまで。