TikZ 実用例（８）～３Dの図を描く～

TikZ は 3D の図（つまり立体、空間の図）も描けるんですね。マジですげー（語彙力）

プリアンブルに \usepackage{tikz-3dplot} と入力するだけで準備はOK♪
あとは平面に描くのと同じ要領で空間の図が描けます。

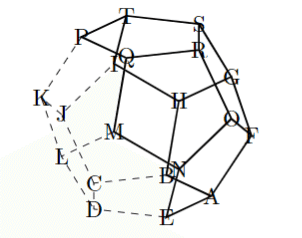
数学A範囲のテキスト作成もあって、正十二面体を描いてみました。
コードはこちら。

\tdplotsetmaincoords{70}{70}
\begin{tikzpicture}[tdplot_main_coords,scale=1]
\tikzmath{ \x=(1+sqrt(5))/2; }
\coordinate (A) at (1,0,0);
\coordinate (B) at ({cos(72)},{sin(72)},0);
\coordinate (C) at ({-cos(36)},{sin(36)},0);
\coordinate (D) at ({-cos(36)},{-sin(36)},0);
\coordinate (E) at ({cos(72)},{-sin(72)},0);
\coordinate (F) at (\x,0,1);
\coordinate (G) at ({\x*cos(36)},{\x*sin(36)},\x);
\coordinate (H) at ({\x*cos(72)},{\x*sin(72)},1);
\coordinate (I) at ({-\x*cos(72)},{\x*sin(72)},\x);
\coordinate (J) at ({-\x*cos(36)},{\x*sin(36)},1);
\coordinate (K) at (-\x,0,\x);
\coordinate (L) at ({-\x*cos(36)},{-\x*sin(36)},1);
\coordinate (M) at ({-\x*cos(72)},{-\x*sin(72)},\x);
\coordinate (N) at ({\x*cos(72)},{-\x*sin(72)},1);
\coordinate (O) at ({\x*cos(36)},{-\x*sin(36)},\x);
\coordinate (P) at (-1,0,\x+1);
\coordinate (Q) at ({-cos(72)},{-sin(72)},\x+1);
\coordinate (R) at ({cos(36)},{-sin(36)},\x+1);
\coordinate (S) at ({cos(36)},{sin(36)},\x+1);
\coordinate (T) at ({-cos(72)},{sin(72)},\x+1);
\draw[thick] (Q)--(M)--(N)--(E)--(A)--(B)--(H)--(I)--(T)
                    (P)--(Q)--(R)--(S)--(T)--cycle
                    (N)--(O)--(R)
                    (O)--(F)--(G)--(H)
                    (S)--(G)
                    (F)--(A);
\draw[dashed] (B)--(C)--(D)--(E)
                        (C)--(J)--(I)
                        (M)--(L)--(D)
                        (L)--(K)--(J)
                        (K)--(P);
\foreach \P in{A,...,T} \draw (\P) node{\P};
\end{tikzpicture}

これをコンパイルすると

と出力されます。

１行目の \tdplotsetmaincoords{70}{70} が

どこから見るかというカメラアングル

を表しています。

\tdplotsetmaincoords{α}{β} とするとき
α が z 軸正方向からの回転角
β が y 軸負方向からの回転角
を表しているようです。

なお、「表裏」みたいな概念はないので、実線と破線は自分で調整する必要があります。
だから、上の図のカメラアングルを例えば {70}{0} にすると

となります。

でも、3D の図が描けるってスゲー（語彙力）