
電気の直列と並列って何?(抵抗編)【大人になって抱く電気のギモン_6】
割引シールをはがして
元の値段チェックしがち
まいど!
理系大学院卒現役エンジニア
兼フィットネストレーナー
サイバーサイエンスTAMOです。
これまでの1~5の記事で、
電流、電圧、抵抗、電力について、
またそれらの計算方法についても
初心者向けに説明してきました。
今回は抵抗の直列と並列について特徴などを初心者目線で
説明していきます。
回路図でいうとこんな感じですね。

日常的に考えるとこんな感じです。

さて、まず電気の特徴をおさらいしましょう。
ある大きさの抵抗にある強さの電圧を与えると
ある量の電流が流れます。
これらの関係式は
電圧 = 電流 × 抵抗
でした。
電気の世界ではこの数式に従って電気が流れる
という法則があります。
この法則をオームの法則と言います。
まず単純な回路で考えてみます。

4Ωの抵抗に40Vの電圧を与えると、
この回路に流れる電流は
オームの法則より電流は電圧÷抵抗になるので
10Aになります。
では、抵抗を1つ追加してみます。
抵抗Aは4Ω、抵抗Bも4Ωとします。

このとき、回路に流れるを求めていきます。
回路上に抵抗が直列な状態で2つあります。
この場合、これらの抵抗を足し合わせます。
合計8Ωになりました。
この8Ωの抵抗に対して
40Vの電圧が与えられるということになります。
なので回路に流れる電流は
40V ÷ 8Ω = 5A
となり、5A流れます。

このように1つの回路の中に、複数の抵抗があって、
それらをかき集めて1つの抵抗とみなして考える場合、
この抵抗のことを合成抵抗
と言います。
では次に抵抗Aと抵抗Bが並列な状態で接続されていたとします。
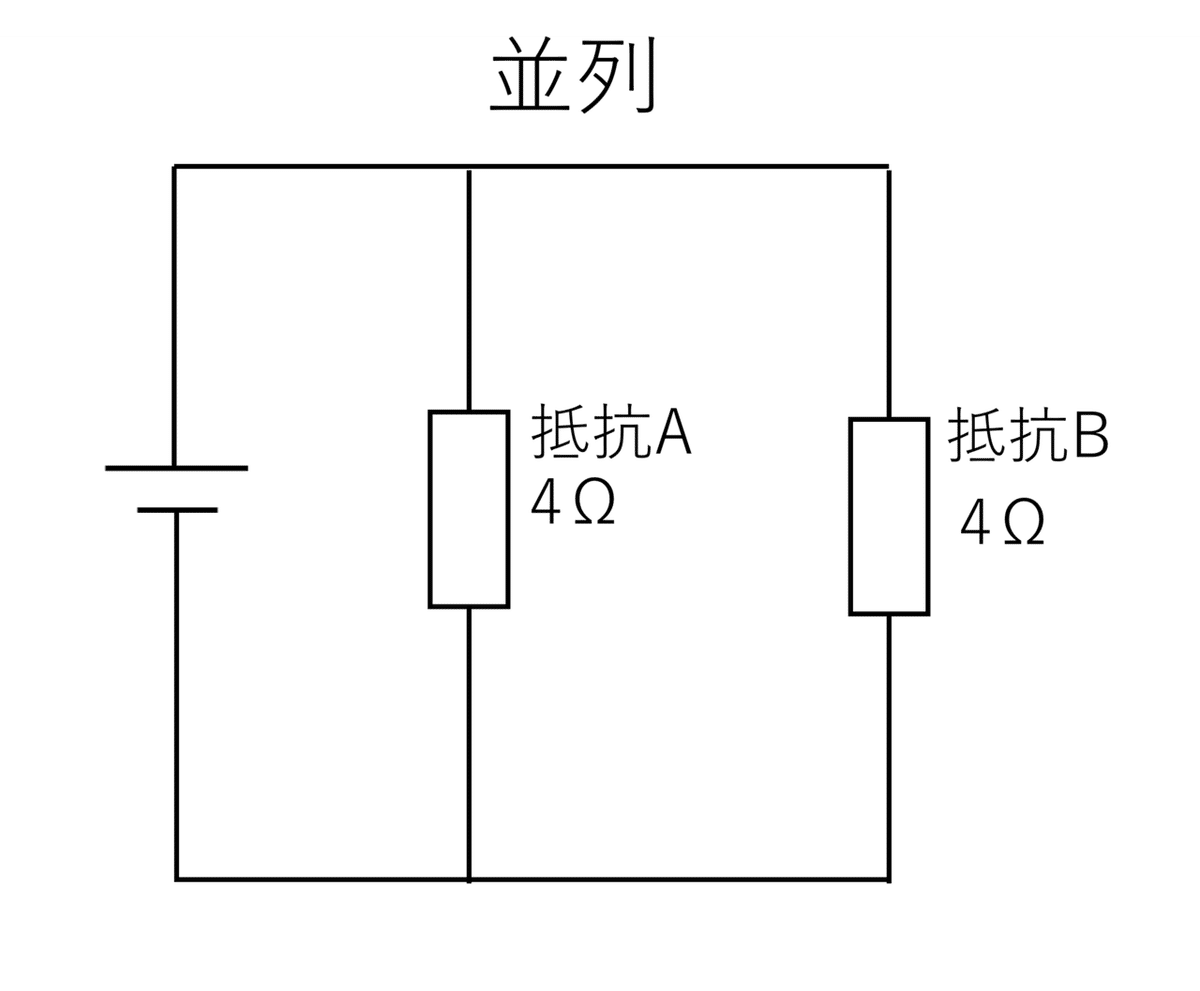
この場合の合成抵抗は、 4Ω + 4Ω = 8Ω
というわけにはいきません。
正解は2Ωです。

はぁ?????
なんで?
っていう声が世界中から聞こえてきましたが、
理由を説明します。
マラソンランナーをイメージするとわかりやすいです。
次のようなコースで大勢のランナーが走っています。
コースの途中に障害物があります。

ランナーは障害物を突破するのに当然ながら少し時間がかかります。
ランナーにとって障害物は抵抗の役目を果たします。
この障害物がコース上に連続して2つあるとさらに時間がかかりますよね?

ではコースが2つに分かれていて、
それぞれの分かれ道の先に障害物が1つずつあるとした場合、どうなるでしょう?

コース上には障害物は2つあるものの
ランナー1人に対して突破すべき障害物は1つのみです。
さらにコースが2つに分かれているため、
後続のランナーは前のランナーが選んだ道と違う道を選ぶと
待ち時間なく障害物に進入できるため、ランナー全体でみると
渋滞が緩和されます。
コース全体で見ると流れが良くなっているってわけです。
もうお判りですね!
電気回路もこれと同じです。
抵抗が直列に接続されている場合、
単純にそれだけ抵抗の大きさが増えますが
並列に接続されている場合、
ある電気に対しては1つの抵抗しか突破していませんし、
回路全体でみると電気の流れ道が2つに増えているので
渋滞が緩和され、よりスムーズに流れることができるのです。
抵抗が1つしかない回路に比べて分かれ道が2つあるので
2倍スムーズに流れます。
ということは合成抵抗として考えた場合、
抵抗の能力は半分になっているので、
抵抗1個分の4Ωの半分なので2Ω
ということになります。
いかがでしたか?
直列と並列はマラソンランナーをイメージすると
簡単に理解できます。
じゃあもし2つの抵抗が同じ値でない場合、
例えば抵抗Aが5Ω、抵抗Bが6Ωだった場合、
合成抵抗は何Ωになるのか?
これについては以下の記事で説明します。
【この記事は近日公開予定】
ではまた!
この記事が参加している募集
この記事が気に入ったらサポートをしてみませんか?
