中学受験：長椅子に人が座る問題の汎用的な解き方　#差集め算

2023年8月21日 17:07

中堅くらいの学校で頻出の長椅子問題(差集め)の解き方。
具体的な出題例は以下の通り。

解き方(絵の書き方)紹介

正確には解き方というより絵の書き方。
問題に沿って説明していく。

以下のように絵を書く。

まず5人ずつ座る絵を左に書く。
2人しか座らない椅子が1脚あり、2脚余る。

次に3人ずつ座る場合を右に書く。
椅子が10脚加わる。座れない子どもが5人。

そして点線を書く。もちろん実線でも良い。
ポイントは線を引く場所。

左右共に規定人数座っている所までで分ける。
今回なら左5人、右3人で座っているとこまで。
両方ちゃんと座ってないと差が一定ではなくなるからだ。

後は線の下の差を出す、今回なら24人。
線の上は1脚につき差が2人なので、24人÷2人で12脚。
後は適当に計算すれば答えにたどり着く。

差集めは「全体の差＝1つ1つの差×個数」で解く。
ポイントは等号の左右を分ける線の引き方。

等号の左「全体の差」を点線の下で計算。
等号の右「1つ1つの差」を点線の上に書く。

問題文を読んで絵を書くと以下の通り。

81人÷1人=81脚。81×5+3=408人

問題を読んで絵を書くと以下の通り。

28個÷2個=14人。子供は17人、アメは14人×8個=112個

絵にすると以下。

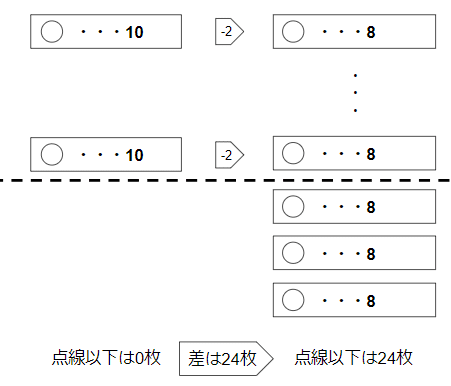
24枚÷2枚=12人。

この解き方(絵の書き方)の良い所は汎用性。
そして理解をそのまま絵にするところ。

良くない解法は理解抜きの数字の操作で答えを出す。
これだと応用がきかない。
この解き方は何をしているか理解して書くので応用がきく。

何人かに教えたがこの絵が理解出来ないという子はいなかった。
逆にこの絵が理解できずに解いてるなら、それは問題を理解せずに解いてる。

問題を読んで絵を書きながら問題を理解し、そのまま解く。
慣れて理解が進めば絵は簡略化してスピードを上げれる。
例えば〇は書かず数字だけとか。