
「浦和ルーテル」2024算数を解いてみた
背景・主旨・総論
2024年1月10日の浦和ルーテルの入試算数を解いたので、その感想考察。
なぜ入試問題を解いているのかは過去記事参照。
「子供に勉強を教えるなら真っ先にやるべきのこと」
解答が見つけれなかったので今回は採点はなし。
むしろ解答を説明していくスタイルで。
四谷偏差値は男子50、女子52。
合格ライン(何点取ればよいか)は情報見つからず。
1月前半試験なので本番2月より1か月早い。
子供が最後1か月で伸びる。
とすると2月のテストと同じ難易度でも正答率は差し引く必要がある。
それを考えると合格ラインは50%いかなそうな難易度。
ということで以下解答と解説。
解答はあくまで自分1人で解いた結果なので厳密な正確性は保証できない。
大問1:計算問題
計算4問。
全てgoogleにも計算させて一致は確認。
(1)3/4÷5/7+6-3/10=27/4
(2)3/2+1/6+3/14+5/21+4/9=323/126
(3)0.3÷52/21×22/7÷0.375=66/65
(4)6.7×107+3+107×5.3=1287
綺麗な数字にならないタイプ。
この辺は過去問見てタイプ分けして臨みたい。
綺麗な数字になるタイプの学校とわかってれば計算ミス見つけやすい。
大問2~6:基本問題
合格ライン50%未満と考えると大問6まで解ければ十分。
大問2:速さ、列車のすれ違い
<問題>
秒速 18mで走る長さ120mの電車Aと秒速 23mで走る長さ230m の電車Bが同じ向きに走っています。 電車Aと電車Bがあるトンネルに同時に入りはじめ,同時に電車全体がトンネルから出たと すると,このトンネルの長さは何m ですか。 解答は答えのみでよい。
<解答>
時間が一緒なので距離の比と速さの比は一致。
Aが進んだ距離:Bが進んだ距離:差分=⑱:㉓:⑤
この差分⑤が列車の長さの差110mになる。
よって①=22m、⑱=396m
396mからAの長さ120mを引いた276mが答え。
①=22m、㉓=506mからBの長さ230mを引いても276mとなる。
というように簡単に確かめ算も出来る問題。
簡単に確かめ算出来る問題はやると良い。
確実に点数がもらえる。
大問3:濃度
<問題>
2つの容器A,Bがあり, 容器Aには10% の食塩水が150g, 容器Bには 20% の食塩水が250g入っています。 はじめに, 容器Aから容器Bに50g の食塩水を移し,次に容器Bから容器Aに 60gの食塩水を移しました。 最後にできた容器Aの食塩水には何gの食塩がとけていますか。
途中過程の式, 考え方もすべて書きなさい。
<解答>
最初のBの食塩:250g×20%=50g
Aから移した50gの食塩:50g×10%=5g
合計55gの食塩(食塩水は300g)
残ったAの食塩:100g×10%=10g
BからAに移した60gの食塩:55g×60g/300g=11g
足して21g
ざっと確かめ算するなら。
10%100gと20%60gで比を使って計算すると14%くらいになる。
160g×14%=22.4gとなりあってそう、とわかる。
大問4:分類分け
<問題>
あるクラスの 28 人に、国語と算数のどちらの方が好きかと, 読書が好きかどうかを調べました。
算数が好きな人は11人, 読書がきらいな人は13人, 国語が好きで読書も好きな人は11人いました。
算数が好きで読書も好きな人は何人いますか。 途中過程の式, 考え方もすべて書きなさい。
<解答>
以下のような表で考える。

全体28人から読書嫌いを引いて読者好きは15人。
読書好き全体15人から読書好きかつ国語好き11人を引くと読書好きかつ算数好きが4人とわかる。
大問5:場合の数
<問題>
クッキーとリーフパイとマカロンを箱に8個つめて友だちにプレゼントします。 どれも少なくとも 1個つめるとき,全部で何通りのつめ方がありますか。 途中過程の式, 考え方もすべて書きなさい。
<解答>
クッキー1なら、リーフパイが1~6で6通り
クッキー2つなら、リーフパイが1~5で5通り
・・・6+5+4+3+2+1=21通り。
<別解>3種で1枠ずつ埋めて、残り5枠と仕切り2つの並べ方
7!/5!2!=21

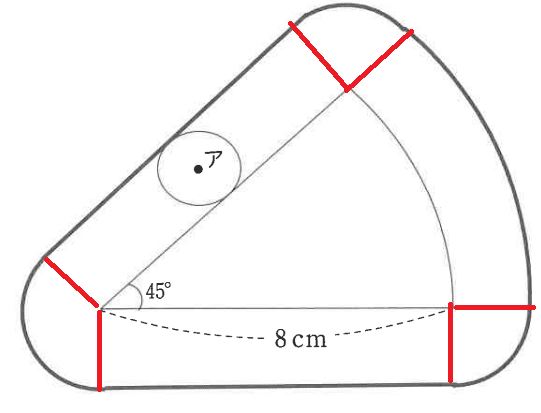
大問6:平面図形、正12角形の面積
<問題>
円周を12等分して, 正十二角形を作りました。 アは円の中心, 円の半径は2cmです。正十二角形の面積を求めなさい。 途中過程の式, 考え方もすべて書きなさい。

<解答>
下のような二等辺三角形12個に分ける。
中心角30度、二等辺が2cm。

この形は有名なパターンで2つつなげて正三角形見つけて計算する。
今回なら2cm×1cm÷2=1㎠
12個だから12㎠。

ちなみに円の面積は2×2×3.14=12.56㎠
差分は0.56㎠だねって話。
大問7~10:中級問題
解けなくても多分合格できそう。
途中式もかける問題で部分を取りに行きたい。
大問7:場合の数
<問題>
円アは, 半径が2cmの円です。 この円が下の図のおうぎ形の周りを1周するとき, 太線の長さを求めなさい。 ただし, 円周率は3.14 とします。 解答は答えのみでよい。

<解答>
以下のように分けて考える。
直線部分は8×2=16
半径2cmの扇形は2cm×2×3.14×315°/360°
半径10cmの扇形は14cm×2×3.14×45°/360°
よって合計37.98
答えだけなのはきつい。
普通に計算ミスりそう。
大問8:場合の数
<問題>
図のように, 小さな立方体を積み重ねて大きな立方体を作りました。
次にア, イ, ウを通るように切り取りました。 このとき,切断される小さな立方体はいくつか求めなさい。 解答は答えのみでよい。

<解答>
とりあえず線が見えている6個は確定。
更に赤線の切断面を考えると赤線の上の立方体も切断されることがわかる。

赤点を付けた3つの立方体は等価なので全て切断される。

最後に中心にある立方体が切断されるかどうか。
下のように正三角形の断面から考えて、中心の立方体は切断されないことがわかる。

よって合計9個。
これも答えだけなのがきつい。
6か9か10くらいで適当に書いても良い。
大問9:立体の体積
<問題>
以下の体積を求めよ(略)。
<解答>
六角柱として捉えれば、六角形の面積×5cmで求められる。
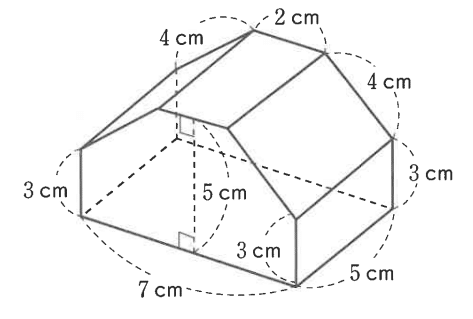
六角形の面積は長方形と台形に分けて計算。
7cm×3cm+(7cm+2cm)×2cm÷2=30㎠
30㎠×5cm=150㎤
この問題は後半にしては簡単に見える。
途中式も書けるし、追加点の稼ぎどころか。
大問10:整数問題
先に言うと問題が会話文なので長い。
(1)は簡単なので拾いたい。
(2)も追加点のチャンス。
(3)は時間があればでよい。
<問題>
母
「今日の誕生日会のために 120個はギョーザが必要だわ。」
たろう
「僕が買いに行くよ!でも駅前にはA店とB店の二つのギョーザ屋さんがあるよ。」
母
「そうなのよ。 A店は6個入りで1皿350円, B店は7個入りで1皿400円なのよ。」
(1) A店でギョーザを120個ぴったり買うときの代金を求めなさい。 ただし, ギョーザのバラ売りは ないものとする。
母
「あ! 調べてみたら,どちらのお店も 11:30~12:30 はランチタイムとして安く買えるみた いよ!」
たろう
「本当に! そんなうまい話ある? ギョーザだけに!」
母
「...ところで, ランチタイムでは, A店は5皿買うと1皿無料でもらえて,
B店は定価の10%引きで買えるみたいね。」
(2)どちらかのお店でランチタイムにギョーザを買い, 最低でも120個用意するとき, A店で買うのとB店で買うのとではどちらの方がどれだけ安いか求めなさい。 ただし, ギョーザのバラ売りは ないものとする。
妹 「私, A店, B店どちらのギョーザも食べたいよ!」
たろう「ちょっと待ってよ。 買いに行くのは僕なんだ!」
母「確かに私も両方のギョーザが食べたい気がしてきたわ。 ランチタイムにできるだけ安く120個ぴったり用意するためには, A店で何皿, B店で何皿買えばいいのかしら。 よしたろうお願いね!」
たろう
「はいはい。 行けばいいんでしょ・・・」
(3) ランチタイムにA店, B店で何皿ずつか買い, できるだけ安く120個ぴったり用意するとき,その時の合計金額を求めなさい。
<解答>
(1)120個÷6個×350円=7000円
(2)A店は6皿の内1皿無料なので20皿なら3皿無料。
17皿×350円=5950円
B店は7個入りなので120個を超えるのは18皿。
18皿×400円×90%=6480円
6480円-5950円=530円 A店の方が安い。
(3)1皿無料を使えるならA店の方が安い。
1皿無料を使わないならB店の10%引きの方が安い。
A店での5皿+無料1皿を1セットとすると、
1セット36個
3セット108個買うとする。
120個ぴったりにしようとするとB店の1皿7個が買えない。
会話的に0皿NGとすると3セットは買えない。
2セット72個買うとする。
残り48個=B店1皿7個×6皿+A店1皿6個×1皿
合計金額はA店11皿×350円+B店6皿×400円×90%=6010円
難しいし時間もないから(3)は捨てて良さげ。
