
「富士見中学」の算数を解いてみた
2022年の富士見中学の入試算数を解いたので、その感想考察。
なぜ入試問題を解いているのか、過去記事参照。
解いてみた全体の感想
まず難易度。過去に解いた学校と比べると以下。
豊島岡>>>女子学院>>鴎友>富士見=共立=頌栄=山脇≧大妻
※大妻と山脇が逆かも
30分あれば全部解けるレベル。難しい問題もない。
大問は4つ。詳細は個別に説明。
1.基本問題
2.頻出整数問題+中央値問題
3.立体の応用問題
4.旅人算の応用問題
大問1:基本問題
本当に基本。問題集に必ずあるレベル。網羅性の確認。


大問2:頻出整数問題+中央値問題
2問ともあまり良い問題に思えなかった。
1問目はよくある整数問題。
悪くないが、記号に置き換える必要性が見えない。
文章で書ききれる。

例えば(3)は「ある整数を3で割った余りと4で割った余りの和が最も大きな値となる整数の内、最も小さな整数を求めよ」でよい。
これだと意味がわからない子供を想定して記号にしたのかもしれないが。
だとすると、次の問題が不可解。
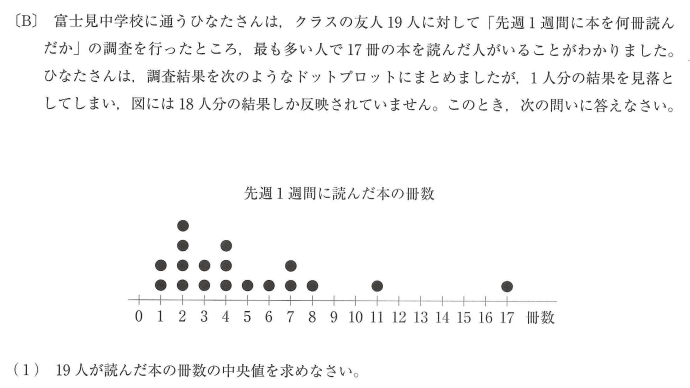
中央値自体の説明が一切ない。
中央値を知らないと、2,3問丸ごと落としかねない。
もちろん中央値は範囲内なので説明は必須ではない。
しかしそれなら前半の「割った余り」の話も範囲内だろう。
片方は例示まで入れて説明し片方は説明なし、というのが気になった。
大問3:立体の応用問題
良い問題。気合で時間をかけて解くこともできるし、演繹的な考えで計算を省略も出来る。
大問4:旅人算の応用問題
複雑性に対応する力を測る問題。
「算数が解けない原因の分解」記事の「3.処理能力」の認知負荷に特化されてる印象。
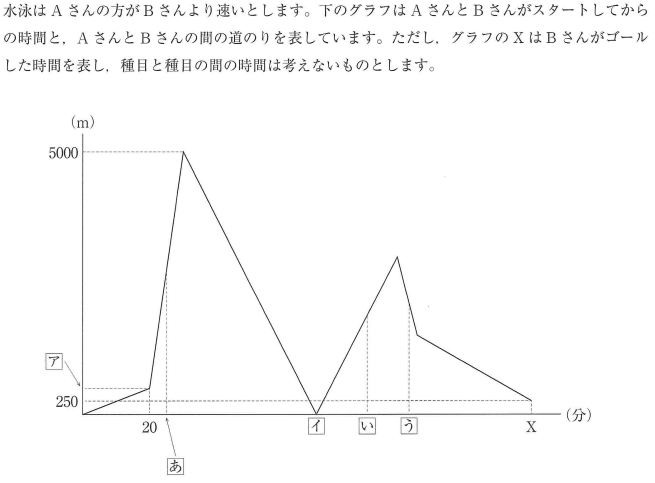
ロジックという意味では"みはじ"以上のものはないが、グラフが差を示してるのもやらしい。
分解すれば簡単だが、制限時間がある入試で最後にこういう問題を解くのは大変そう。
メモの取り方(数字の書き入れ方)にセンスが求められる。
この記事が気に入ったらサポートをしてみませんか?
