Bombeとかいうゲームについての手記 その32
このnoteは私が淡々と頭の中を整理するために書くnoteです。
過度な期待はしないでください。
前回さっと流したOneScoreのルールについて。

こいつ思ったよりも強いかもしれない。◯個とはっきりわかっている情報を他に伝播させていくようなルール。特に伝播されるのが一番質の高い情報であるのがポイントかも知れない。これと◯個のときだけを解けるルールですら、かなりの範囲を解ける。やはり概念拡張……!概念拡張はすべてをなんとかできる……!
ちなみに+とか-も同じようなことができるが、+でやるとあまりの数の爆発的増大に耐えきれなくなってPCが死ぬ。◯個ちょうどの情報はそれ自体があまり多くないことと、拡張するとさっと解けてしまう情報のほうが多いのでこれ自体はそれなりに有用。

直近の追加でこんなに活躍してるやつなかなかいない。

コスパはそれなりとしても、やはりCPUは喰う。それだけがしんどい。誰か新しいPCくれませんか。

実はこんな感じの少し日和ったルールは作っていた。こっちはもっとコスパがいい。

優先度を下げているのもあるが、かなりコスパいい。こいつがあるおかげでさっきのやつのコスパが下がっている説も少しある。
コスパとかCPUの関係でもう一つ。

いつだか作ったこんなルールだが、結構重かった。そして盤面上に解けるはずの情報が出ていても、概念拡張によって-やら+が用意されないと解けないという問題があった。つまり、このルールを用意していても、

このルールもまた有用だということである。こっちは◯個限定の情報から、概念拡張無しで適用できる部分しか解かない。これはすごくCPUに優しい。


だからたとえ同じ種類であっても、両方用意しておくだけの価値がある。ということである。CPU大事に。ハングしてゲームが落ちたら悲しいし。

なんとなくできてしまった謎ルールの考察。

0確定が多すぎる。弄っている途中でルールの根本がすり替わっている気がする……。これあれか、3ルールのときの拡張か……。

盤面を解いたときはこっちだった。なーんでこうなってるんでしょうかねえ。

多分このルールがさっきのに変わってしまう以上、!2が大した意味がなくて、1-,2-から既に!2が1であることが確定している気がする。

そんなこと無いか。これちゃんと真面目に考えないとダメなんだろうな……。こうやってどんどん私のCPUと私の脳が消耗していく……。

わかんないけどこれからなにか言えないだろうか。

何もいえんなぁ……。cを!2の範囲と完全に被らせれば2のパターンは消せるがだとしても……。
わからんので置いておこう。
次はいつもの盤面検討。



1/2/3→3-、2/3→2+、2→2+と置き換えても成り立つ。
さてこのときにまずマス目は不問である。

本当はもっと不問で、

こうなるのだが、一旦0が多い状態にしておく。考えづらいので。
2+と2+の合計値は4+なので、このルール上は必ず4つ以上は入るはずであるが、その入る予定のマスはすべて1-と3-に属するので、それぞれ1,3個、つまり最大値の爆弾を入れないと成り立たない。その爆弾の振り分けは2+:2+について、1:3、3:1しかない。つまりどうあがいてもその通り爆弾が入るので、2+2+の範囲に属さないマスはすべてクリアできる。

その場合に2+同士が重なるマスが許されるかどうかだが、これはルール画面の中央のマスだけ許される。これは、至極当然の理由で、本来重なった部分に入れてしまうと、2+2+について4+にならず、最小で2つの爆弾がその条件を満たしてしまうのだが、逆に1-3-に置いても重複するマスであれば、意味上の違いはないということである。この条件を式にすれば、

としたときに、方程式:χ+ψ=κ+πとなるような整数すべてがこのルールを満たす。つまりこの論調ではこのゲームでは文字化が不可能である。
多分何かしらほかの観点から文字化が可能なのであろう。一旦横においておいて、作業を進めるだけで検証可能なものをいくつか検証しておく。

とにかく似たようなパターンを大量に作って実際に盤面を解決できているのか検証してみた。このうち最も活躍しているのは今回作成したルールである。まあ解けていない盤面から導かれたルールなので、ある意味当たり前とも言える。
しかしもう一つ注目して欲しいのは、1-1-1+1+などのいかにも適用自体できそうなルールさえも適用がないこと。これはつまり、このルールを適用前に解けてしまうということである。特に+と-が同じ数字で重なっている範囲を保つ場合は、

こういうルールで解けてしまう。そう考えるに、-の数字と+の数字が一致しないパターンが特に4ルールのみで適用があるのだろう。

おそらくこういうパターンもどこかで適用があるはずである。

そう思って作ったら早速適用された。

逆にレアパターンなこともあり、あまり適用可否判断自体がされないせいか、CPU自体もあまり喰わない模様。
ちなみにだが、おそらくこのようなルールさえ適用すれば2ルールで解けるはずである。



ただこれはものすんごく重い。加速度的に情報が増えてCPU爆散不可避。
見つかったときに個別で設定しておくほうが幾分かマシな気がしている。
次の盤面。
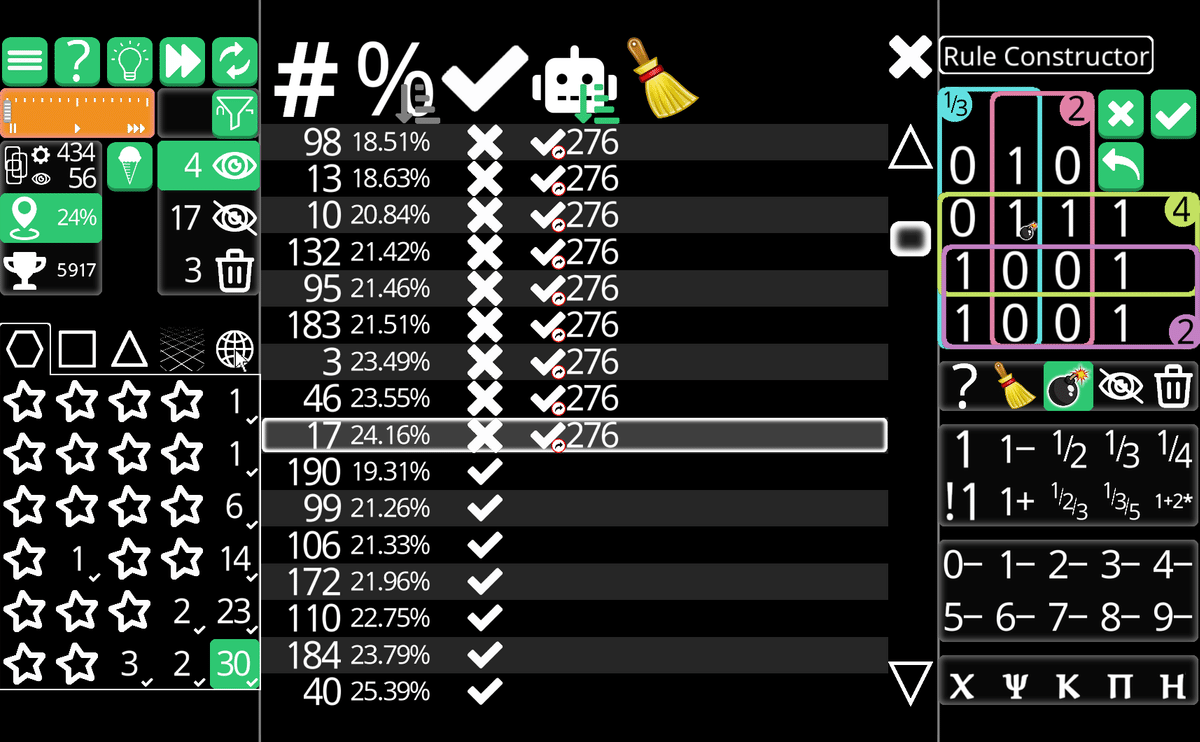


ちなみに、
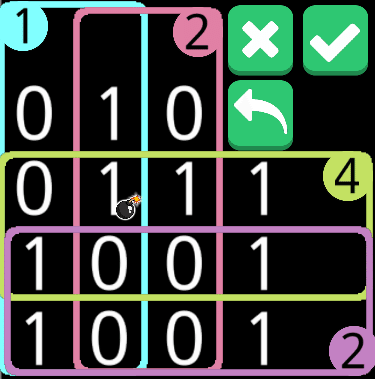

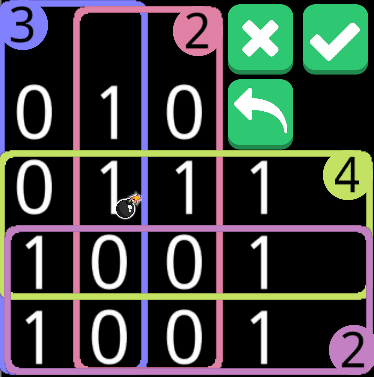

1+、3-で成り立たないことから、溢れる系で検討を進めても回答は得られないであろう。また、2では成り立たない。

!2で成り立ってしまうので、個々の爆弾の条件は0,1,3,4であるが、


0,4はそもそも不可能(非論理ではなく)なので、そもそも成り立つのは1,3だけである。さて、ここで以下にして爆弾の値が定まるのか。2から見て爆弾でない位置を確定させる方法が手っ取り早いのではないか。
最上段真ん中が爆弾でない場合、上段の2の範囲はすべて爆弾である。4の爆弾の埋め方は色々考えられるが、下段に2つ爆弾を入れると2は満たせるものの1/3に矛盾が生じる。よって入るのは上段に1つ、下段に1つ。下段はどちらに入ってもよく、右に入れた場合は1/3の範囲は爆弾でない。左に入れた場合は1/3の範囲は爆弾となる。
上段真ん中が爆弾でなかった場合、最上段真ん中と上段右が爆弾である。4の範囲に残り爆弾が3つあるため、残りのマスはすべて爆弾である。そうなると2の範囲において最下段には爆弾が入らないはずだが、1/3の範囲については最下段に爆弾が入らないとおかしいため矛盾する。よってこの箇所は爆弾でないということはありえない。
上段右が爆弾でなかった場合、最上段真ん中、上段真ん中は爆弾である。4の範囲に残り爆弾が3つあるため、残りのマスはすべて爆弾である。そうなると2の範囲において最下段には爆弾が入らない。この時点で1/3は満たされているのでこのパターンはあり得る。
よってありえないのは上段真ん中が爆弾でないパターンのみなので、ここに爆弾が確定する。

最上段真ん中のマス目は実質1であるので?になる意味がない。(2以上の爆弾が入る場合は4と矛盾する)最下段は先程の考察の通り最終的に入る可能性を検討するだけの箇所なのでマス数はどうでもいい。

素直にχとしてみた。これは成り立つ。

そのまま次数は下げられない。どこかのマス数と連動するのだろう。

逆に上だけ次数を下げることはできる。じゃあ右と上の関係性やいかに。

右と上は全く関係ないみたいです。本当かよ。

右側はあふれる系を使ってるみたいです。助けてくれBombe。お前が何を言いたいのかよくわからないよ。

右側についてはあふれる系が右側だけの関係性で完結してるみたいです。

右しただけ次数を下げても成り立つ。しかもそうするとだいぶマス目不問になる。なんで?

ここまで来ると上もあふれる系に直る。なんでだよ。えーこのまま考えますね……。
まず何と言っても(ψ+κ+π+2)+から考えなければならない。(それ以外は何も確定できる要素がない)
κとπのマスがあるので、少なくとも上段下段にψ+2この爆弾が溢れ出す。上段のマスは2マスなので、下段に対して最低でもψ個の爆弾があふれる。この個の時点でψ+πを満足してしまうので、残りのマスはすべてクリアできる。

そうなればあとは簡単で、他の文字によらず上段の爆弾は確定しているので、χ=2以上のときにこのルールは成り立ち、あとは最上段左に爆弾が入るか入らないかである。証明終わり。
意外と簡単だったが、やはり趣旨がぶれている。やはりあふれる系に直したのが間違いだったのだろうか。でもこれで元の盤面は解けないのだろうか。
χ=2,ψ=0,κ=1,π=1のとき、3-,2+,4+,1-……成り立たない。どこかで余計な変換をしている。そうか、右下の個数だけ次数を下げたときだ。だからそれ以降の考察は何も意味がない。
だからその時点での文字化が最大限の文字化なのだろう。改めてそのルールで考察して終わりとする。

κとπのマスがあるので、少なくとも上段下段にψ+2この爆弾が溢れ出す。上2つのマスは爆弾で下段がψマスあるとみるべきだろう。



意味ない!!!!!じゃあそもそもψがいらないのか。


まだ大本の盤面から導かれた制約を守っている。多分これは大丈夫。
さて、もう一度。κとπのマスがあるので、少なくとも上段下段に2個以上の爆弾が溢れ出す。3マスのうち2マス2爆弾を入れるので、残り1マスに付いて爆弾を入れないとして仮定していく。
上段真ん中が爆弾でない場合、上段右と下段左は爆弾である。χ+1の範囲に残り爆弾数がχであり、最下段はπ+1が満足されたので全てクリアされる。
必然的にχ個の爆弾が最上段真ん中に入るので、χ/χ+2の範囲にχ+1個の爆弾しか存在していないことになる。つまり成り立たない。
上段右が爆弾でない場合。上段真ん中と下段左は爆弾である。χ+1の範囲に残り爆弾数がχであり、最下段はπ+1が満足されたので全てクリアされる。
必然的にχ個の爆弾が最上段真ん中に入るので、χ/χ+2の範囲にχ+2個の爆弾が存在している。これは成り立つ。
下段左が爆弾でない場合、χ+1の範囲に残り爆弾数がχ-1であり、最下段にはどこか1マスに爆弾が一つ入る。この時点でχ=0の場合はこのパターンは存在しない。(χは1以上)χ+1の範囲の最下段に爆弾が入る場合、χ-2個の爆弾が最上段真ん中に入る。(同様にこのパターンはχは2以上)最下段のうち最下段右に爆弾が入る場合はここで矛盾する。χ/χ+2に対してχ-1個しか爆弾が入っていない。最下段のうち最下段真ん中の場合はピッタリχ個入っているので条件は満たされている。
最下段最右に爆弾が入った場合、やはりχ/χ+2に対してピッタリχ個入っているので条件は満たされている。
最下段左に爆弾が入った場合、χ/χ+2に対してχ+1個の爆弾が入っているのでこれも成り立たない。
よっていくつか成り立つパターンが存在し、それはすべて該当箇所が爆弾である場合である。
また、すべて爆弾である場合も考えられる。(盤面とは異なるが設定するルール上はあり得る)
この場合は最下段左に爆弾が入れば成り立つ。これで合計がχ+2となり一致するからである。あるいは最下段右に入っていても成り立つ。
以下は最下段にそれぞれ入るパターンである。考察の通り最低でもχが1以上もしくは2以上となっているのがわかる。







0/2が2であるとき、右が0/1である。左が1/2である。

残りの爆弾の入り方は以下の通り。


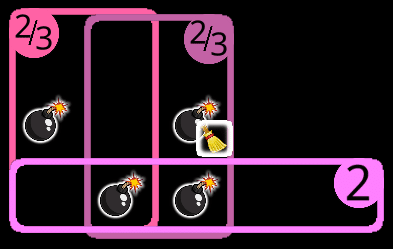
一方で0/2が0のとき、
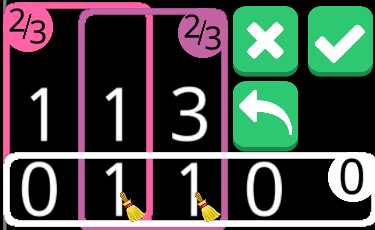


こうなる。うーん……何も……。やっぱり最低でも4ルールでなにか見出すしかないのか……?

この4ルールでなにか考えてみる。2/3から考える。
3マス中1マス爆弾でないあるいは全て爆弾のどちらか。
①すべて爆弾である場合、最下段右も同様に爆弾であることが確定する。下段最右は爆弾でないことが確定しているので、最下段最右は爆弾でない。

②最上段左が爆弾でない場合、残りの2マスが爆弾である。最下段右も同様に爆弾であることが確定する。下段最右は爆弾でないことが確定しているので、最下段最右は爆弾でない。

③上段左が爆弾でない場合、残りの2マスが爆弾である。最下段右も同様に爆弾であることが確定する。
赤枠部分は未確定である。
③-1:上段最右に爆弾が入る場合、残りのマスは爆弾が入らない。
③-2:下段最右に爆弾が入る場合、最下段最右も爆弾が入る。

④最上段真ん中が爆弾でない場合、残りの2マスが爆弾である。0/2が0であるので、最下段右も爆弾でない。最下段最右は未確定である。

何も、成果が得られませんでした……!1の範囲とか確定しそうだけど確定しない。うーん。とはいえ、1の範囲に2/3の範囲が被っていることからするにほぼほぼ爆弾だと思うのだが。だとすると、この部分に爆弾が入らないとパターン数が少なくなる感じの情報を一緒に突っ込めばもう少し実りある検討ができるかもしれない。うーん……。もう少し具体的に表現しないとダメか。重なっている範囲が爆弾でないとき、1と!2の範囲が未確定なのが良くない。ここで!と!2の範囲が確定していて、それが他の情報を元にすると不可能であればそのパターンがありえないので、この箇所が爆弾であると確定できる。うん、そうだろう。だとすれば……?

これで検討すればよいのか。というかそれ以外無いよなあ多分……。
①すべて爆弾である場合、1の範囲の残りが爆弾でない。あとは確定しない。残りのマスには1つ爆弾が入る。

②最上段に1つと上段左に1つ入る場合、①とほとんど同様である。
ただし赤枠部分には1つではなく2つまで入る。(1/2)しかし、最下段に2つ入ることはない。(!2の制限)

③上段左に爆弾が入らない場合、①と同様のところまで全く同じに進む。

しかしここでは終わらず、赤枠部分の振り分けによって爆弾の位置が変わる。
③-1:最上段右に爆弾が入る場合、最下段右は爆弾が入らない。その場合最右はどちらも爆弾の可能性があり確定しない。
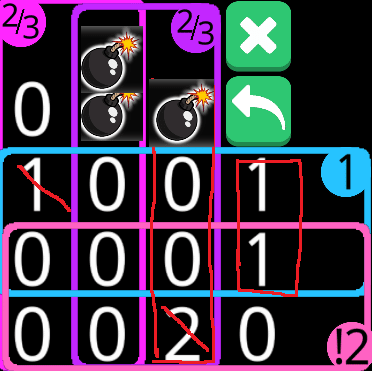
③-2:最下段右に爆弾が入る場合、最上段右には爆弾が入らない。!2の制約により最右のうち爆弾が入らない。上段最右に爆弾が確定する。

割と可能性広いな……。ここまでで先程の検討結果と矛盾するような結論は得られただろうか?
③上段左が爆弾でない場合、残りの2マスが爆弾である。最下段右も同様に爆弾であることが確定する。
赤枠部分は未確定である。
③-1:上段最右に爆弾が入る場合、残りのマスは爆弾が入らない。
③-2:下段最右に爆弾が入る場合、最下段最右も爆弾が入る。
全て図にまとめました。つまりこうです。(説明放棄)

なんかおかしいよなぁ!0/2のほうの内訳から見ると、この場合はどうあがいても最下段の!2の部分に1つは爆弾が入るはず。だから2/3での③-1はあり得ない。また2/3から見れば、!2の最下段は2個入ることはありえない。(2/3の制限に引っかかる)だから、0/2の③-2はありえない。そうなると、残りは2/3のほうの③-2、0/2のほうの③-1しか残らない。これは1と!2にとっては同じ配置。つまり1のみの範囲に爆弾が入り、!2と1以外が重なる範囲に1個爆弾が入る。このパターンを盤面に図示してみる。

1の残りのマスは爆弾でない。2/3より爆弾位置が確定して、0/2の爆弾位置も確定。!2の残りのマスは爆弾が入れないのでクリア。2/3の部分が未確定で残る。
……あり得るんじゃん!ということはもしかしてこれ逆にアレか、緑位置が爆弾でないことが確定するのか。そんなうっすいところがここまで確定しないの!?
このまま盤面で埋めてみる。

あり得ない。これはありえない。2/3の制限をオーバーしている。

この場合が全然確定しない。!2か2/3から埋めていくのが良さそう。!2にしてみるか……。


ということは緑色の位置が爆弾の場合は!2は常にすべて爆弾?そしてそれが矛盾を導く?

0/2が0のとき

0/2が2のとき
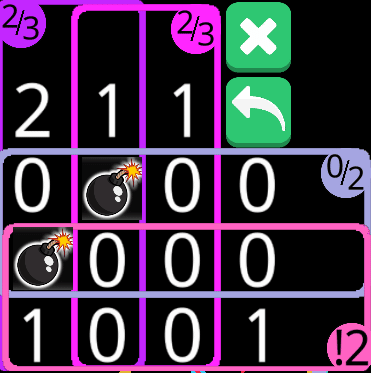
2/3の爆弾の位置次第で確定する。




答えわかってるのにルールがわからん……。1と!2が重なる場所は絶対に爆弾じゃない。仮に爆弾だとすると2/3の爆弾位置が確定して、0/2で爆弾が増えて!2の範囲はすべて爆弾になってそれが2/3と矛盾する。だから少なくともここが爆弾であることは絶対にない。ないんだけど。それがどのような論理に基づくルールで排除されているのかがわからん……。

こういうことか?でも4マスについて!4ってつまり3-ってことだよな……。クリアできん……。でも結局この組み合わせでなんかするんだろうな……。本当にわからんので解散……。
