Bombeとかいうゲームについての手記 その39

このnoteは私が淡々と頭の中を整理するために書くnoteです。
過度な期待はしないでください。

色々重くなりすぎて辛かったので、暫くの間、とにかく軽いルールだけ作っていた。そういうルールをいくつか拾って汎用化できるか試してみる。
今回検討するルールはこちら。

真ん中にχが入らない以上、χ+1しかありえない。左がクリアできる、としたほうが軽い気がする。

1を文字にしたい。この場合に1という数字が意味するのはなんだろうか。
左側に爆弾は入らない。それは左に1個爆弾が入ると真ん中にχ個爆弾が入ってしまうからだ。そうだとすると、!1ということではないか。

2個以上の場合にもこれで対応できる。しかし真ん中の爆弾の個数はχ+1個以上なのは確定するが、それ以上は確定しない。

---

χもしくはχ+3である範囲にχ+1が確定している場合、残りの範囲に2個が確定する。これは同様に、

χ+2との選択の場合でも成り立つ。ただし文字化はできない。それはここの数字が選択先の数字との差分-1であるから。

3択の場合はもう少し複雑になる。この場合は1または3個入ることになる。

選択系の場合に、その範囲のうちにある個数の爆弾が確定したとき、ルール化できそうである。

χであれば0/2/4

χ+1であれば1/3

χ+2であれば0/2

χ+3であれば1

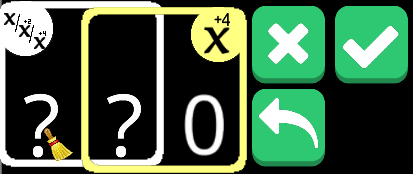
χ+4であればクリアできる。また、それぞれ+のときに以下のように成り立つ。

---

よくわからない。χ+1ということはつまりすべて爆弾であるが……。0のときと2のときを想定すればよいだろうか。
0のとき、上段左にχ+1を入れても下段左にψ+1個以上溢れる。よってこの場合は上段左が爆弾で下段左がψ+1で下段最右が0個になる。
2のとき、上段真ん中に爆弾が入るパターンと入らないパターンがある。
入るパターンのとき、下段右にも爆弾が1つ入る。ということは下段の残りの爆弾はψもしくはψ-1になる。上段左にχ+1個爆弾が入るとすると、上段の合計の個数はχ+2個になる。よって下段左に入る爆弾の個数はψもしくはψ+1になるが、前述の通りに下段の残りの爆弾の個数はψもしくはψ-1なので、下段左がψに確定し、下段最右が0個になる。
入らないパターンのとき、下段の残りの爆弾はψ-2もしくはψ-1になる。上段左にχ+1を入れても下段左にψ+2個以上溢れるので、このパターンは不可能。
どちらにしても下段最右は爆弾ではない。

ψを以下系に直す。χも以上系に直す。

0/2は1が成り立たないだけなので、2*にする。

---

最近発見したこと。
!χなどの否定形は概念拡張するだけなら割と簡単にできる。例えば、

間が抜けている選択式は当然に否定形に直せる。
また、以上以下の場合も同様に、

と直せる。つまり、

こういう場合も成り立つ。(選択式が以上以下の意味を包含しているので、当然成り立つ)

選択式の間の部分に否定形が成り立つので、この場合も成り立つ。また、以上以下を内包するものとして、

偶数奇数系もあり、こちらも同様に否定形に変換できる。ではこれでなにかいいことがあるのかと言うと少し微妙。
4ルール系だとピンポイントでχでないことさえ言えれば確定する部分があるので、そういうときに使える、というところだろうか。