Bombeとかいうゲームについての手記 その19
このnoteは私が淡々と頭の中を整理するために書くnoteです。
過度な期待はしないでください。
今回検討する盤面はこちら。




過去に類を見ないくらい理由のわからない内訳表になった。
aに入る爆弾の個数はそれぞれ0,1,2,3+が考えられる。それによりbの範囲が定まり、bが定まるとcも定まるが、cは特に否定形を含む爆弾の個数になっていることに留意すること。また、cには?(すべての数があり得る)パターンがある。少なくともルールにする以上はこの?はすべて否定しなければならない。

?を見ればわかるがbに3つ以上入る場合はルール化不可能である。よって少なくともbの欄は2個以下である必要がある。

b欄のマス数が2個以下の場合が上記の表である。ここでルールを作るに当たって、b欄は全く見る必要がない。何故ならばbによってcが一意に定まるため、具体的に定めるのはcのほうが都合が良いからである。

流石にわかりにくいので否定形を箇条書きにして0,1,2,3+に分けた。
3+はとりあえず3としてもよいはずなので一旦3と置く。
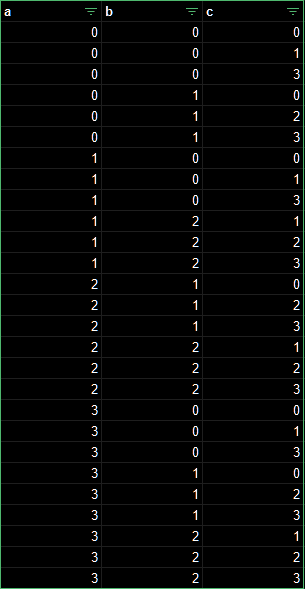
パターン数が多すぎる……。ともかくaとbとcをなんとかしてみる。

とにかく合計値を求めてみた。ここで盤面を思い出してみる。2/4というヒントがあったため、最初にそれを考えてみる。

ここで盤面ではa,cが2マスだったため、爆弾の個数が3個である場合は除外できる。

盤面ではbが1なので0個なのが確定する。

とりあえずこれはルール化しておく。そしてもう少し考察してみる。

2の場合は内訳が確定する。

ほかも見てみたがあまり興味を惹かれるものはなかった。
もう一盤面やりたいと思う。




とりあえずマス目は不問のほうが多いようだ。

下段は2の倍数で条件は足りているらしい。


d+e+fが奇数の場合は不可能。

eだけが0確定。
さて逆に不可能である場合は常に奇数であるということを鑑みれば、

奇数の場合はbが0というルールも作れそうである。

これらのルールは意外と適用されていて、偶数奇数というのは存外に手強範囲が広いものだと再認識した。

また、1-の特別性というのも一つの要因としてある。1-は0/1ということであるが、範囲内に1個爆弾が確定してしまえば他のマスはすべて0になってしまう。これは少なくとも1つ入りそうなマスが存在すれば他の領域に区切られたマスはすべてクリアできるという特別性により、自身の持つ情報量がかなり多い情報なのだろう。
さて最後にもう一盤面。


ぐちゃぐちゃであるのでルール一つで改善するかは怪しいところだが、今回考察したいのはこの盤面のうち、右下の部分だけである。具体的には、

ここらの4/5、5/6あたりの情報を整理したいと思っている。

最初に4/5のペアからなにか言えないか探ってみる。

なおその17では同じ種類の情報が同じ範囲に存在した場合のみ考察していた。

aが1マスまでの範囲では上記の通りになる。なお、今回の場合はcも1マスのため不可能と示したパターンもあり得ない。

aまたはcが0であると仮定すると、真ん中の共有する範囲は少なくともχ+になる。しかしそれは元々、

このような概念拡張に含まれるルールに記載されているためなにか新しいルールではない。今度は一般化してから考える。


上記表を見ると少なくとも下記ルールが成り立つ。

χ/χ+1が被っている場合に重なり合ったセルの個数がχ個以下であれば、少なくともそれぞれのみの範囲に1個以上の爆弾がある。
上記表を元にすれば、a,cに爆弾が入らないパターンはbに爆弾がχ個あるいはχ+1個入ったときのみなので、マス数的に入らない場合は必ずa,cには爆弾が存在する。
また、a,cが1以下の場合は少なくともbはχ以上である。

盤面に適用できるかであるが、

今回の盤面では上記のようなものは存在したが、適用されそうな情報はなかった。
さて次に下記のような場合を検討する。


a,bは先程と同じで、χ+2とした場合のcだけが異なる。



こちらも先ほどと同じようなルールを見出すことができた。
次に、下記のような場合を検討する。


先程までのパターン表で示したものと同じパターンしか無い。
このパターンでも全く同様のパターンが見いだせるため、相互の数値の関係性とこのルールから導き出される情報の間には関連性がないということがわかる。つまり、




こういったルールが成り立つ。次数を下げるかつ+を導くルールはあまり役に立たないという経験則に基づけば、χ+を導くルールは不要だろうか……。

適用数を見てみるとそんなに悪くはないのだが……。
