Bombeとかいうゲームについての手記 その33
このnoteは私が淡々と頭の中を整理するために書くnoteです。
過度な期待はしないでください。
今回検討する盤面……の前に。
今まで非表示機能をよく使っていた。

こういうやつ。でも全てオーバーラップしてTrash……破棄にした。具体的にはこう。

本当はあんまり良くない。例えばχ/χ+1と(χ+1)-は厳密には意味が違う。なので非表示が適切である。本当は。でもね。

やたらと処理が軽くなるんですよ!!!もうこれ以上複雑な盤面は破棄していかないと無理かも!!!ということで破棄していくことにした。情報自体は欠落がないはずなので、細々と個別ルール対応すればクリア自体はできるはず……。
そんなこんなで盤面検討。


うっそでしょ……こんな簡単なルールまだ抜けてるの……?

こうなります。χ+1はみ出るので(χ+1)-だと該当箇所が爆弾確定で、χ/χ+1は(χ+1)-と等価なのでこれは成り立つ。


うっそでしょ(略)
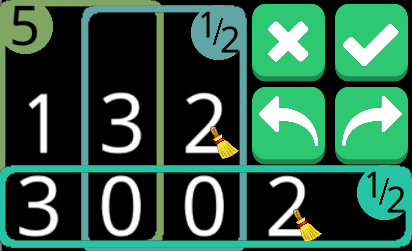

あれ、なんかこれ思ったよりも難しいな……。ちょっと真面目に考えないとダメか……。でもそんなに元の盤面の方は難しくないはず。
5から溢れるのは4つというので間違いないはず。その場合に1/2が独立しているから、それぞれの範囲に爆弾が2個ずつ確定して、残りのマスは自動的に爆弾でないことが確定するはず。

あっ、こうか。それぞれの範囲が5に別々にアプローチしてくるのか。

次数を下げるとこう。


うっそ(略)


そうか、おそらくだが、この簡単な盤面が残っているのは1が1-とかだと多分ルール設定されているということだろう。情報を積極的に破棄しているので多分適用するタイミングがないのだろう。

なんかややこしくなったんですけど。


2個あふれる系で、1と1-に配分されるのは同じ。でも溢れ先に!2もあるから成り立たないな……。
クリアできる場所に爆弾が入っていた場合、最下段左に爆弾が入らない。これは1-と1によって他の箇所は0に確定しており、最下段左に入れると!2と矛盾するから。だから、その入り方はできない。故にここはクリアできるのだが、1は1-になるがほかでは成り立たないだろうなぁ……。このままで決定。

もっとややこしくなったが。

よく意味が……。


爆弾らしいが。!2の意味は0/1/3というところ。こうなっているときの否定形が本当にめんどくさい。定型化できないし。

すごく厳密に個数が要求されている。4から考えるのが丸いか。
4から見て2個以上あふれることになる。その場合は多分成り立つ。溢れない場合を想定する。まず爆弾が4つ溢れた場合。
爆弾が4つ溢れた場合、上段真ん中に爆弾2つ、下段左に爆弾1つ、最下段左に爆弾一つ。下段右に爆弾が1個確定して、3-と矛盾する。

3つ溢れた場合のうち、上段に1つ入れる場合は!2と矛盾する。

下段、最下段に1つしか入れない場合は1/3と矛盾する。



あふれる個数によって左上が定義されているのはわかるがそれ以外の関係性は定式化できるのだろうか……。それ以上の汎用化は一旦放置。




上の方はすべてあふれる系らしい。それぞれχ+3以上、κ+2以上あふれる。
χから見て3に1個爆弾を入れれば、残りはχ+2である。κ+2個あふれるとしたのでκ+"からχ+2を引いてκ-χ+1個上段下段に入るとすると最下段にはχ+2個あふれる。その場合に3の範囲に入るのはχ+3個なので、χは常に0である。

つまり徒に左上の個数を増やせないってこと。この盤面で同じように考えてみると、ψのところから3つ以上、κのところからκ+2個以上溢れる。κ+2と3だとどちらも満足してしまうが……。いやちがう。ψの溢れ先はつねに3に属するから3は必ず満足される。そして2個分だけκの領域に溢れるから、上のかっぱ範囲から右のかっぱ範囲に入るのはκ個だけでいいのか。

このときπ+2は必ず溢れてしまうので不可能。なので、右は必ずκ+3の値を取る。そのうえでも該当箇所だけは必ず爆弾でないと合わない。またψ+4にもならない。

最終的にχは右下に対応できた。でも3以下だと成り立たないのでこんなに次数が高い。

全然盤面が解決しねえ!

だいぶ解けそうではある。


きっと溢れ出るだろうの精神。

文字がもう一つあれば最下段もできそうだが……。

まだ終わらないんですけど!しかも5情報か……。

なんとか解けそうな形。
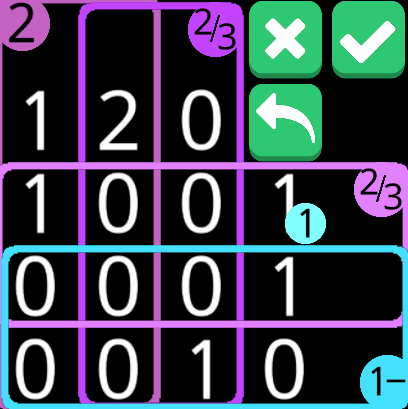

どうせ溢れるだろうの精神。ちなみに左上の2は爆弾でないことが確定するマスなので溢れる系ではない。ってか溢れる系なら爆弾マークでいいか。

さっきと同じような形。
溢れる系で考えると、ψ以外のマスにχ+1溢れる。
そして1-を見ると2に対してχ個溢れることがわかる。そこまでに2/3の範囲に入っていなかった場合、爆弾が最上段真ん中に確定する。入っていた場合(最大でも1個までしか入らない)最上段真ん中が1個に確定する。残りの爆弾はχの個数次第で0~1に変動。ということはχは0or1か。あんまり文字化する意味ないな。

まあ文字が余っているならいいか……。

1マスずつしかあかねえ!

でも盤面自体は解けそう。というかさっきのルールでκのみに属する範囲がクリアできるってだけか。





はいはい、あふれる系あふれる系。


あふれる系を単品で置換するときに文字2つ使わなくてもいいか……。今回の上みたいに他の要素と混ざって文字にできる場合はしてもいいけど。
該当箇所がクリアできない場合、つまり爆弾の可能性が残る場合とは、0でなく、かつ爆弾位置が1個以下しか確定していない場合。
χ+ψの箇所からχ個溢れるが、例えばχ+1の方向に溢れたとすれば残りは1個。πの範囲から見れば2+が溢れるので、πの範囲内に爆弾が1個溢れればχのほうは満足するので、必然的に下段最右に1つはいって終わり。下段最右に1個入れば、その時点で(π+2)+が満たせなくなる。

なのでこのパターンは如何にしても該当箇所がクリアできる。逆にχ+1の方向へ全部は溢れないパターンだが、この際に上段左に溢れる個数は1この場合だけ検討すれば良い。何故ならば、2個入った場合は該当箇所がクリアできることが自明だからである。
さて、上段左に1個入った場合、下記のようになる。

0/2には残り1個しか入らないが、入れるべき爆弾は4つ以上ある。このときに、πのみの範囲がすでに存在しないため、πからあふれる爆弾は0/2もしくはχ+1の範囲に入る。0/2に入るとき、該当箇所がクリアできることが自明。χ+1の範囲に入る場合、0/2の範囲でもある箇所であればやはり該当箇所はクリアできるので、残るマスは最下段右しか無い。最下段右に1こはいる場合はπから見て残りの爆弾が0/2に入らざるを得ないのでそれもダメ。最下段右に2個はいる場合、χ+1が満足されるため、やはり該当箇所はクリアできることになる。故にどのパターンにあっても該当箇所はクリアできる。

うわあああああ(椅子から転げ落ちる)

ヒントが3ルールだったのでヨシ!


まーた溢れる系だよ。

そりゃそうだ。多分このルールは同じ意味のものはあるんだが、片方だけ以上系になっているのが無いのだろう。……あれ、解けないんだけど。いやそっか意味違うな……。合計が5になるんだもんな……。

こうか。
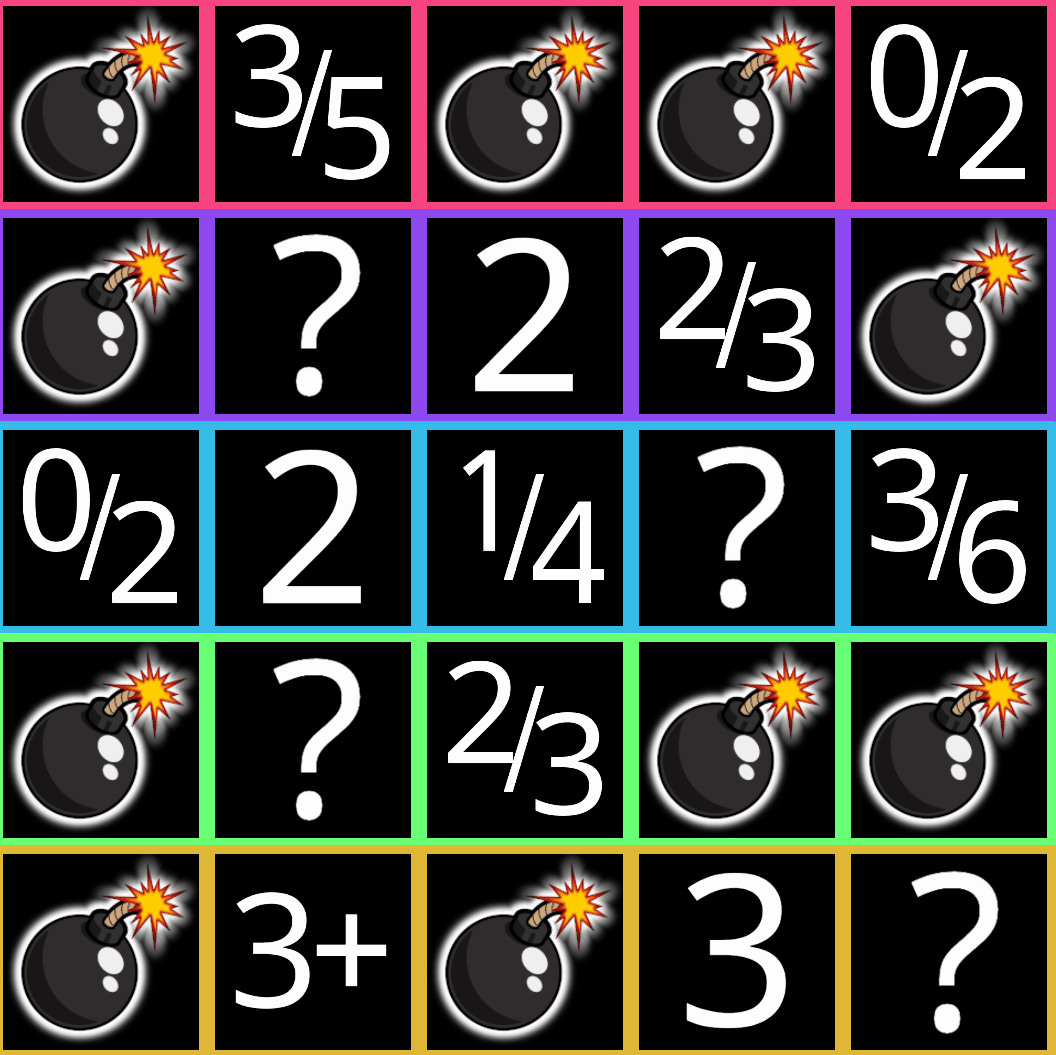
とけた。次回は溢れる系についてまとめてみようかな……。
