Bombeとかいうゲームについての手記 その31
このnoteは私が淡々と頭の中を整理するために書くnoteです。
過度な期待はしないでください。
今回検討する盤面はこちら。

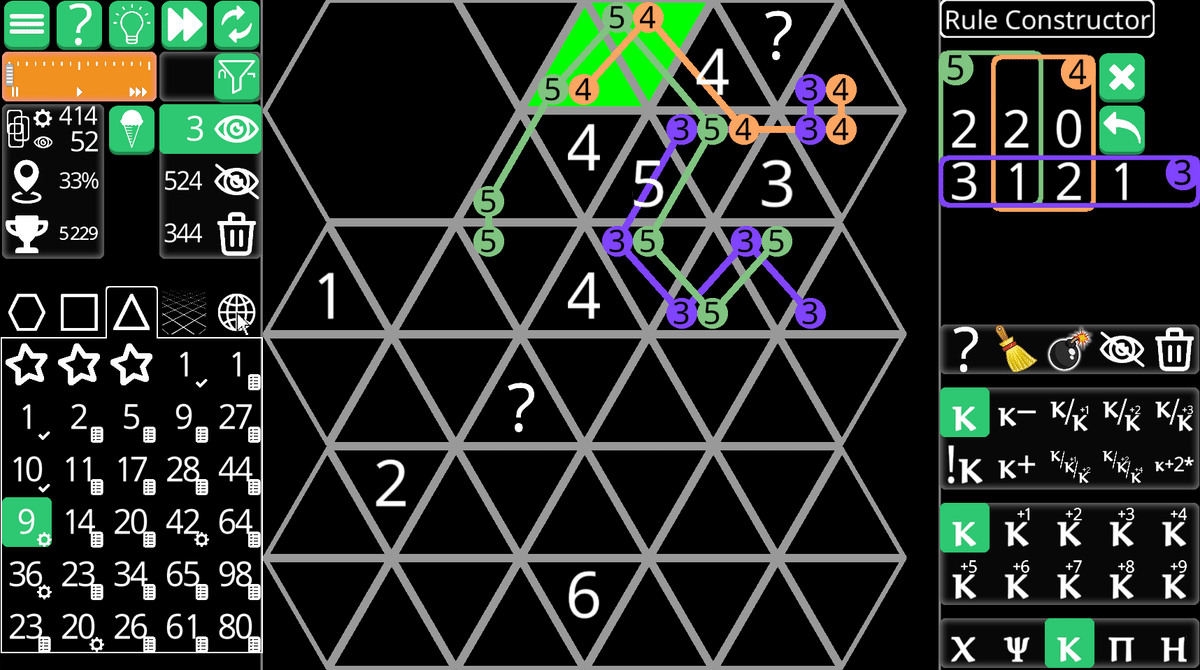

前回こんなの作らなかったっけ?


なんかちょっと違う……。まだ最適化できるのかな……。とにかく5と4の内訳表を見てみる。

うーん……。4を起点に考えてみる。これも前回のものと同様に4の分け方はb,cについて22または31しか無い。
22に分けたとき、5について2個、3について2個または3個埋まっている。
2個埋まっているとき
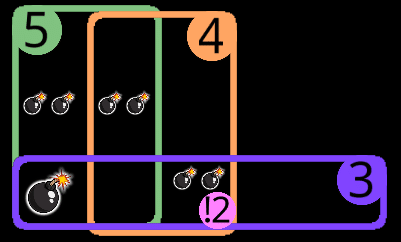
3個埋まっているとき

3個埋まっているときは、実質31に分けたときと同様だが、マス目の制限を解除して考えてみる。

このような内訳になる。上段真ん中が常に爆弾2つはいるのはどうしてだろうか。合計マス数が5つということは爆弾でないマスが1つしか無いということである。爆弾でないマスは上段真ん中に入らない。これは5と3の関係性からである。
うーん、一般化したあとの姿が見えてこない……。あまりよろしくないが、マス目が不問である箇所を特定し逆に検討してみる。

このくらいはまず汎用的にできた。……わかったかも。
これは4を起点にするのではなくて、4と5をそれぞれ検討しなければならない。
4+から見て、下段には2個以上爆弾が溢れる。
5+から見て、下段には1個以上爆弾が溢れる。
故に下段は確実に3個爆弾が入る。
溢れ先を検討すると、
4+から見て、下段真ん中または下段右へ溢れる。
5+から見て、下段左または下段真ん中へ溢れる。
共通するのは下段真ん中なので、下段に溢れる爆弾を最小にしようとすると、下段真ん中に爆弾が入るパターンが最小で、その数は2である。(下段真ん中に1個、下段右に1個)
その場合3-を満たす場合は下段最右に爆弾が1個入る。
下段の爆弾の個数については一般化できる。左の溢れる個数+右の溢れる個数-共有できる下段のマス数=爆弾の最大個数であれば、上段の真ん中が爆弾確定、ということになる。
左の溢れる個数は上段左+上段真ん中-左の爆弾の個数、右の溢れる個数は上段右+上段真ん中-右の爆弾の個数となる。具体的に示すと、

左の溢れる個数:a+b-e
右の溢れる個数:b+c-f
g=(a+b-e)+(b+c-f)-d=a+2b+c-d-e-f
となる。うん、一般化できたけどこれは文字足りないかも。bとdを一旦固定値としてみる。b=2,d=1とすると、
左の溢れる個数:a-e+2
右の溢れる個数:c-f+2
g=a+c-e-f+3
話が前後してあれだが、この盤面の場合はぎりぎり成り立つのは2-のときか。

無制限に小さくしていいわけでも大きくしていいわけでもないので、成り立つのは2以下または3以下のとき。2以下のときはいいか……。これは多分2ルールで解けてしまう。aが2マス、bが1+?マスcが?+?マスになり、(χ+ψ)+とχ-に対するルールが使えてしまうだろう。

2マスに対して2+が確定するので爆弾だとわかるだろう。だからこの場合は検討しなくて良い。なので検討すべきは3-のときだけ。

すべて同じ文字列であれば成り立つ。なので次数を下げられる……

訳では無い。溢れる個数が下記の場合は足りない。

あっ!前回やったやつかも!

これと同じ形で、下段真ん中を文字化できる例なんだ……!えっ文字足りるのかこれ!?ちなみにdが増えるとκ-としている箇所の爆弾個数が減るはず。それって文字化できるのかな……。このゲーム文字の減算できないんだよな……。

こうやん!減算はできないがκが関係するところにすべてηを足しておき、減算されるκ-のところには足さない。足さないので実質マイナスという小賢しいテクニック。
χ=2,ψ=0,κ=3,π=1,η=1とした場合におそらく先程の盤面を解けるのではなかろうか。代入してみる。

……解ける!解けるはず!これ多分設定がχとψで逆だっただけでほかは一緒で先程の盤面になるはず。実際解けた。

しかしすごい時間がかかった。多分完璧なルールなのに!
次は謎盤面の検討。


なんで40%超えてる正解率なのにここまでやってて解けてないんだろう……。


赤枠部分に3個溢れる。白枠部分に1個溢れる。赤かつ白の箇所には最大で1個しか入らない。4この範囲に対して最小の溢れ方をするためには共通の部分に1個入るため、
緑の部分に2個、青の部分に1個溢れるのが最小である。この時点で4の範囲について残りは2個である。この場合は1が既に埋まってしまっているため該当箇所は0個である。
次に1の範囲に極力入らないように設定すると、

緑の部分に3個、紫の部分に1個溢れることになる。その場合もやはり、該当箇所はクリアできてしまう。こちらは既に4つ埋まってしまっているから。
さて、まずは以下・以上系に変えてみる。

OK。次にロジックを元に変えられそうなところを変えてみる。溢れる個数によって溢れ先の個数を変えればよいはずなので、

その一方で3+を4+にするときはマス数制限がある。

うーむ。法則性は何となく分かるものの、とんでもなく面倒な気が……。

そうか、爆弾1個分の遊びを持ってる感じか。ううむ。
結局該当箇所に入らないというのは既に4を満たしているもしくは既に2を満たしているのどちらか。溢れる個数は上記の例でいうと、4個と1個であり、既に4を満たしているもしくは既に2を満たしているのうちどちらも満たさない最大許容量はそれぞれ3個と1個で、必ずどちらかは満たしてしまう。

だからこっち方向も連動して増えていい。ということは4文字ではないのかこれ……。

とりあえず連動する個数を文字にした。プラスはマイナスと連動する。これめっちゃ重そうだが……。

あれこれπ消しても成り立つな……。でも消せるならもっと文字使えるか?

ちょーっと尋常じゃなく重いかも。さっきの盤面成り立つのかな。
……成り立たないじゃん!πがなくなったことがやっぱり影響してるじゃん!!!どうしようかな…。+-消せばなんとかなるかな……。

+-消したら負荷的には大丈夫になった。うーむ。PCの買い替えすら検討に入るぞこれは。
次の盤面。そろそろヘキサゴンクラスは全部かたしたいところだが……。





0/2,2/3の内訳表。

cに2個爆弾が入らないことを確定させれば、bに2個爆弾が入ると確定できる。
そしてcに2個爆弾が入ることはない。何故ならば、仮に2個入るとすると、爆弾が1個の範囲について他に入れるべきマス目が存在しなくなってしまうからである。だからこそ該当箇所が爆弾、あるいはクリアできるマスとなる。

マス目は不問で……いいのかな……。いいんだろうな。マス目が増えることによって得られるパターンのいずれも、1のマス目に爆弾が一つ以上入るパターンのように思える。要は該当箇所のクリア自体はできてしまうので、少なくともこのルールについては不問なのだろう。

1を1-に、2/3を2+へ。やっぱり溢れる個数を考えたほうが良いかもしれない。
1-の組へ溢れる個数を考える。

2+から見てこれが最小の爆弾個数であるが、この場合は0/2の制限に引っかかるので赤枠部分へ1個溢れる。
1個溢れたときに、どのように入れても該当箇所はクリアできる。

また逆に0/2から見ても同様である。0/2が0のとき下方向へ溢れる個数が最小であるが、これは同様に2+の制限から1個溢れることになる。あとは場所が違うだけで同様の論理で該当箇所はクリアできる。
直感だが判断の軸は2+においたほうがいいだろう。

話を整理するとこの様になった。まず(χ+ψ+κ+1)+から見てψ以外のマスにχ+κ+1個溢れることになる。さて、次に1-の組に最小になるように溢れるとすると、κ+1の箇所にκ+1個入れるようになる。さて、左の爆弾の個数を見ると、どうやらもう1つは爆弾を入れなければならないので、やはり1個溢れ出ることになる。
左へ溢れ出る個数をκ個にすれば左の範囲からは溢れ出ないが、(χ+ψ+κ+1)+のほうで1個溢れ出ることになる。よってあとは実際の盤面の通りに該当箇所をクリアできる。
うーむ、こんなところだろうか……。0を文字にできそうな、出来なさそうな……。1-の組は多分無理のような気がしている。これは1-以外だとパターン数が増えて溢れ出る個数を増やしただけではどうにもならない気がする。
次の盤面。




この確定の仕方は間違いなくあふれる系であろう。
5+は下へ2つ以上、3+も下へ2つ以上溢れる。受け取る側は合計で最大4なので、仮に4つ溢れる場合は最大数の受け入れ可能な配置でなければならない。それは具体的に言えば2-の共通する部分に爆弾が入らないように入れるしか無いので、その場合の配置は下記である。

溢れる数が合計で3つの場合も存在する。が、その場合は最大受け入れ可能な配置を取れないことを意味する。具体的には下記である。

どちらにしろ該当箇所は爆弾に確定またはクリアできるのでこれは成り立つ。

つまり個数が制限されるのは上記の通りになる。文字化すると、

こうなって、おそらく上部の2は右側の爆弾の個数から来ているので、

こういうことになる。文字数足りないんですけど。ちがうか。3ルールなのか。

おそらくこれが最小だろう。どちらにしても1個溢れるルール。……本当か?多分だが4ルールにしておくことで任意の1-で区切ってマス目数を一致させることができているのが便利な気がする。そしていつだか作った

こいつのほうが適用範囲が広くてさっぱりこれを使って解いてくれない。

3-くらいまで作っておけば大丈夫だろうか……。
番外編。
実績one scoreについて
正直良くわかっていないが、爆弾の個数が20個である手がかりを作成しろと言うのがこの実績解除の条件。
60-ルールで達成したが、当然他のルールでも再現可能。
ルールを先に示す。
Bombe Rules (5):
💣⠨⢵⠯⣽⡣⡂⣯⠺⠅⠣⠂⡕⠄⠀⠤⠃⡻⠢⡲⡵⡬⡥⡧⡲⡯⡵⠰⠬⠢⡰⡡⡵⡳⡥⡤⡲⡩⡯⡲⡩⡴⡹⠶⠵⠳⠱⠳⠲⠸⠲⠬⠱⠹⠶⠸⠶⠴⠰⠬⠰⠰⠰⠳⠴⡝⡽⠠⢰⡀⢋⡁⣒⡢⢿⠈⠻⠡⡢
⡶⠃⡻⢜⡰⣥⢆⠶⢂⣫⡲⢨⡕⡘⠅⢿⠂⡢⡦⣇⢾⡥⠀⠉⣜⢋⠒⠉⡏⠚⠐⠛⡂⢖⡦⢇⡇⡰⠸⡜⣳⢫⡯⠴⢪⠮⣋⡙⣨⢴⠌⣤⣺⠇⡑⠭⠆⠐⢓⠖⠬⢝⠁⠲⠼⢀⢠⣣⠁⠁⠛⣫⡄⠂🛑
対象の盤面はここ。


他の盤面を実行しようとするとクソ重い盤面もあるので注意。上記のルールでここまでは来れるはず。
参考:"Making 20: In 60 rule mode, build enough clunky rules to unlock the left Triangle column, then build the rule shown. Then autosolve."
上記のルールだと重すぎて死ぬ盤面が多すぎて少し軽量化したものを使った。これだと重くなりすぎる盤面は幾分か減る。
