Bombeとかいうゲームについての手記 その15
このnoteは私が淡々と頭の中を整理するために書くnoteです。
過度な期待はしないでください。
今回検討する盤面はこちら。




少なくともならないものはならないので、このルールが成り立つということは良いだろう。多分。
マスの数の話だけすると、aとbについてマスの個数は問われない。これは2/4に対して、0/3の条件に基づけばcの残りマス数が1であれば常に0はありえないからである。(左の条件が仮に0だとするとa,bの爆弾数は常に0であるので2/4を満たすには少なくともcに2個以上の爆弾が必要になる)

0/3において0が成り立たないのは2/4においてのみならず、2以上であればOKである。2以上というよりは、右のルールによりcに爆弾が確実に入り切らず、bに1個以上爆弾が入るときである。つまり、


こういうことである。

左側の条件はψ(何らかの整数)にはならない。これは反例のとおりに、χ+1がψと同値の場合はψのときも成り立ってしまうからである。
bが1+であることが確定したとき、左側がψ/ψ+1などの表記である場合一体何が言えるだろうか?
少なくともψ=0である場合は成り立たないのでそのパターンは除外できるだろう。また、χとその範囲にのみ含まれるマス数の関係性によってはみ出す個数が定まるため、例えばこのように表現可能である。

この場合bにはみ出す爆弾の個数はκ個である。
似ているルールをいくつか既に設定していたのでそれも合わせてみてみる。

はみ出す個数が常にχ個の場合のみのルール。これは下位互換なので削除すべきだろう。

χ個以上はみ出すときに、χ個以下と範囲が被っていれば0のマスが存在するルール。

当然上記の場合は同様にbの部分がχに確定する。
ここらへんのルールは1つか2つくらいにまとめられそうである。
肝心なのは、とにかく特定個数がcからはみ出すこと。すべてその前提を共有している。
左の爆弾の個数がχ-とされている事が多かったので、それに習って考えてみる。盤面に当てはめると、3-となるだろうか。
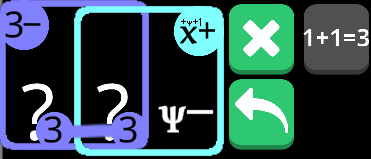
まずこのようにした。ここでbが(χ+1)+が確定する。χ+でも良いが、χ=0のときに0+となってしまうので何も判明しないため、χ+1としている。

さてこのときに左の範囲の爆弾の個数が特定の数だったとする。例えばκ-。
このときaの爆弾の個数は{κ-(χ+1)}-である。

おそらくこういうことだろう。上記ルールにおいて、やはり同様にbにχ+1個がはみ出る。左の範囲の爆弾の個数がχ+κ+1個以下であるとき、χ+1個以上bに確定しているのでaの個数は当然にκ個以下になる。
のだが、これも無制限のためルールにはならない。無制限なのは何故だろうか。それはψが0であるパターンにおいて繰り返し適用できてしまうからだと考える。
χ=0,ψ=0,κ=1のとき、

この様になる。ここで生まれた1-の範囲は1+とは……被らないですね……。被るならばたしかに無制限なのだが。無制限の定義がなにか違うのだろうか?
このルールを適用しようとすると無制限に代入が必要になるのか?

とりあえずマスの個数を限定してみても無制限に成り立つので、無制限という言葉の意味は無限回適用できてしまうからダメと言う意味ではなさそう。では何がダメなのか。

英語のお勉強からしましょう。無制限という日本語には曖昧な意味しかありませんが英語なら……!
無限という意味よりは際限のない、という方が正しそうな気がする。
要は整数の全てで成り立ってしまうがために、組合せ数が膨大でゲームがハングしてしまうということだろうか。(都合よく適用してほしいなあ)
ではまあ無理だとして、どのようなパターンならルール化できるのかという点について考える。マス目の制限はかけても無駄なので、いちばん重要なのは文字の数を減らすことだろう。そこを無制限と表現するかどうかのラインとしているっぽいので。

例えばこのようなルールは適用できる。
これを適用しようとするとχがかならず定まるので大丈夫なのだろうか。


とにかく無制限と書かれるルールを探してみた。例えばこれはほとんど同じルール。左になにか-があって右に+がある。すべてのマスの爆弾の個数の合計は単に足し算をした場合と一致するから、上のルールは成り立つ。こんなルール作る気無いけど。
下のルールは右側にπを足した状態。これだと無制限になる。なんで?そもそも成り立つのかこれは。無制限を保ったまま簡単化できないか試してみる。


少なくとも得られる結果が文字でない場合は良いみたいだ。
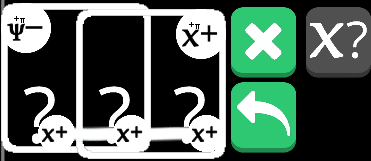
これは本当に成り立つのだろうか。
χ=100,ψ=0,π=0としてみる。
左は0個以下。つまりa,bは爆弾が入らない。一方でcはその条件から100+であり成り立つ。成り立つなあ……。
χ=100,ψ=0,π=1としてみる。
左は1個以下。つまりbは最大でも1個、最低では0個しか爆弾が入らない。cはχ個入るので、やはり合計は101個なので、100個以上(100個もしくは101個)入ることになる。成り立つか……。
χ=100,ψ=1,π=0としてみる。
左は1個以下。つまりbは最大でも1個、最低では0個しか爆弾が入らない。cには100または99個入るため、合計はやはり100個以上となる。成り立つのか……。
おそらくルールとして成り立ちはするのだろう。しかし組合せ数が多いのではなかろうか。もう少し簡単化してみる。

これはいいのか……。左辺を一意に定めれば右辺を定めることができるのが重要と見た。つまり、左辺か右辺か、どちらかを確定させればルール適用有無がはっきりわかるもの以外を無制限と呼んでいるのだろう。多分。そう思えば先程の

これがOKで、

これがダメというのは一貫性がある気がする。ではこのルールで問題になっているのは右辺か左辺かどちらかを1変数で表せばよいということになる。

実際の盤面に戻って、0/3を3-,2/4を2+と読み替えていることを念頭に置いて、既存のルールが何故適用できなかったのかを考える。

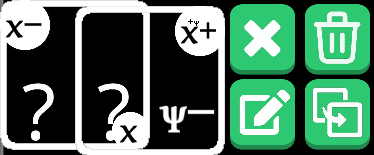
0/3を3-,2/4を2+と読み替えるルールが存在しない
ルール適用されるような変数の置き方をしていない

1は否定された。既に2+,3-の情報は盤面に出ている。
では2であろう。ルールを改めて見返してみると、マイナス側の数字は必ずプラス側の数字と同じかそれより小さい値しか取れない。ここがダメなのだろう。
そうなっている主な原因はプラス側のセルの個数を文字で表しているためである。でもここをあんまり数字にしたくないよなあ……。
では、発想を逆転させて3-の数字を下げられていないのが原因ではないだろうか。2-にできればすべてが解決する。

するとちょうどいいところに1/2があった。1/2は1+であるので、

こうなって……ダメっぽい。これではないのだろうか。

ではこっちからなにか言えないだろうか。具体的にはaとcの関係性を。

これしか成り立たん……!何もわからん……!2マスに対して0/1/2ってことはノーヒントだろ……!
では反対にプラスの方を何とかするのかもしれない。


盤面を確認したところ、3-の情報は初出であった。イケるかも!

こうなって、
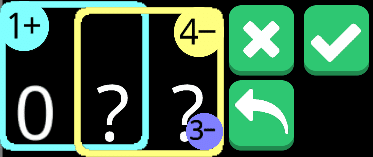
こうなって、

こうして

こうじゃ!
……盤面が!動かない!どうして!?
4-と1+もないのか?

4-がない。何故?と思ったが、4マスに対して4-というのは情報価値なしのため出ないようにしていたらしい。それは正しいが先程作ったルールが適用されないのは困る……。
逆に情報価値がないということは、右辺置き換えが間違っているのかもしれない。そして気付いた。
2マスに対して3-なのは自明。なのでこれは情報価値なし。
この盤面、何を確認したら解けるんだっけ……。(迷走)


ヒントによるとここがクリアできるらしい。
最初の検討は0/3,2/4の2つから始めた。得られる結論はa,bに爆弾が3個。そのうち爆弾が1個である範囲と被っているので、残りのマスには2個の爆弾が入ると仮定する。そのため、2/4と被っている範囲について少なくとも1または2個の爆弾が確定する。1または2個のどちらであっても4ではないことが確定するので、2/4は2である。そしてそのうちの爆弾2のは入り方は2通りあって、aに1個入るパターン、aに爆弾が入らないパターンである。そのときのbの爆弾の個数はそれぞれ1個、2個である。どちらにしても色付きのセルがクリアできるのは、前者のパターンはあり得ない。仮定したときに既に爆弾の個数が1の範囲に1個爆弾を配置しているからだ。よってこの過程のときはaは爆弾ではなく、bに爆弾が2個入る。そのため色付きセルはクリアされる。

では仮定が間違っている場合はどうか。要するにaに爆弾が入るパターンである。この場合は逆に1の範囲に他に爆弾が入らないため、他のセルが0個であることが確定する。その時に爆弾の3個を入れなければならないが、色付きセル外に少なくとも2個以上の爆弾が入る。そのときに2/4の範囲に対して既に3つ以上爆弾が入るため、2/4は4となる。その場合2+の範囲はすべて爆弾で確定のため、やはり色付きセルには爆弾は入らない。
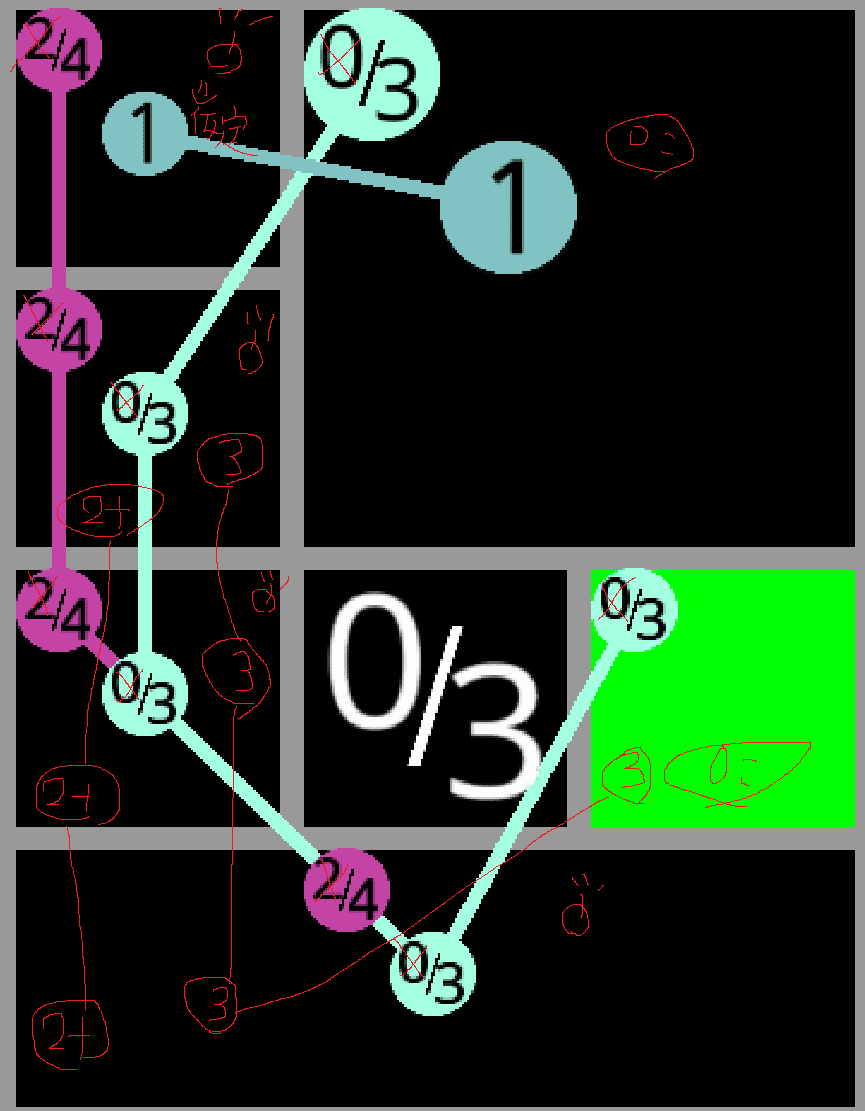
なのでどちらにしても色付きセルの箇所はクリアできる。やはり0/3が3に確定するのが肝のようだ。そりゃそうだ。
この盤面がいつまで経っても解けない大本の原因は過度な汎用化ではないか。少なくとも○○個はみ出すルールは2ルールで網羅できているのではないだろうか。ここで重要なのはやはり0/3と2/4の範囲が被っていることであり、それが一番の手がかりなのではないか。つまり、

これでいいんじゃないかということである。ここから〇〇個以上には置き換えられないのではないか。

できたわ。できたけどこれ以上はやっちゃあかんのではないか。
これもやっぱり○○個はみ出すルールのうちの一つにはなるが、爆弾の個数が3個以下では成り立たない。

成り立たない理由は右辺を成り立たせる可能性が残ってしまうからである。反例の通り例えば1+のときには成り立たないし、2+でもやっぱり成り立たない。それが成り立つのはχ/χ+◯の形のときだけである。


同じ形で+1,+2,+3のときに成り立つのだが、他のルールは必要なのだろうか……。
