Bombeとかいうゲームについての手記 その4
このnoteは私が淡々と頭の中を整理するために書くnoteです。
過度な期待はしないでください。
さてその3にて色々書きながら最適化してみました。その4以降はしばらくこういった最適化の試みをそのまま書き連ねていこうと思います。
今回検討するのは下記の通りです。
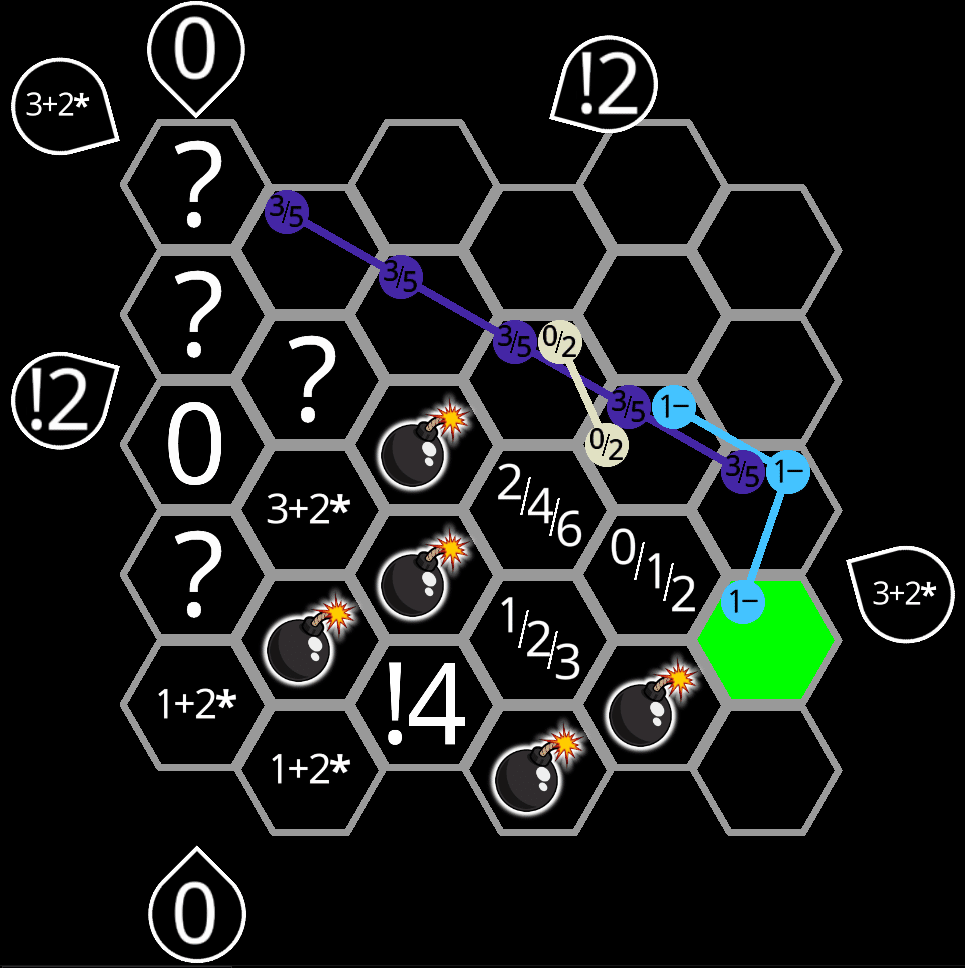

ヒントによればこの通りのルールを元にマスを開けられるとのこと。
さて、この場合の爆弾の内訳を検討してみる。

さて、その3での盤面と同様にこの盤面もパターン数は少ないです。

右下の3/5となっていますが実際には3しかありえません。これは0/2がどちらの場合でも1-の制限に引っかかるため、すべてを爆弾にするパターンが存在しないからです。まあ深く考えずとも内訳を見ると必ずどこかは爆弾が入っていないのでわかるでしょう。
1-を変化させてみます。


2-にするとaの個数が確定できなくなります。なのでおそらくこの1-であった部分の個数に着目するのはおそらく悪手なのでしょう。一旦他の部分に着目します。3/5のうち5が使えないであろう状況を確定させているのはどういった要素か考えます。
3/5の範囲に含まれるマスは5マスです。つまり3/5:5ということになります。この状態でその範囲に含まれる爆弾が5個ではないと確定できるとき、すなわち『うち一つが爆弾を含まないとき』に、5個ではないということになります。ここで『うち一つが爆弾を含まないとき』という情報をもたらすのは一体何でしょうか?それは0/2と1-の関係性です。つまり3/5の範囲のうち、0/2に含まれる部分に爆弾があるとき、1-に含まれる部分に爆弾がないと証明できれば、その範囲に含まれる爆弾が5個ではないと確定します。
さて、その目線で再度2-にしたときの爆弾の個数内訳を見てみると、2-では3/5の範囲について5のパターンが存在します。


ここで先程書いた、『3/5の範囲のうち、0/2に含まれる部分に爆弾があるとき、1-に含まれる部分に爆弾がないと証明できれば、その範囲に含まれる爆弾が5個ではないと確定する』という事実を用いるため、盤面を少し簡単化します。こんな盤面を考えてみることにします。

マス目の個数について検討します。b,c,dに当たる部分はマス目は何でも良いはずです。何故ならば爆弾の個数内訳は下記のようになるからです。

何マスあろうと、爆弾は一つまでしか入らないため、上記のパターン以外は検討不要です。つまりマス目は関係ないので?にできます。

さて、では更に盤面を縮めます。この盤面ではどうでしょうか。


これが3/5から5を省ける(おそらく)最小の情報です。
『3/5の範囲のうち、0/2に含まれる部分に爆弾があるとき、1-に含まれる部分に爆弾がないと証明できれば、その範囲に含まれる爆弾が5個ではないと確定する』という観点からすれば、aは3以上のマス数になりそうですが、実際には不可能ではないパターンのすべてのマス数で成り立ちます。(bが2マスなのでaは1マス以上であることが確定し、2-の爆弾の個数が0であることもありえない。それ以外のパターンではすべての想定されうるマス目で成り立つ)
さて、ここから再度数字を変更してみましょう。








さて、傾向が掴めてきたでしょうか。爆弾の個数内訳が一番傾向がわかりやすいと思います。
左上の爆弾の個数は考えなければならないパターン数を示します。具体的には爆弾の個数内訳のaの行数が増えます。
次に3/5のうち3が確定する爆弾の個数になります。(5を弾くにはどうすればよいかを考えて設定しているのである種当たり前ですが)
3に当たる部分が上昇すると、aのありうる爆弾数のうち最も少ないものが不可能になります。
さて、3つの文字が見えてきたでしょうか。

まず3/5はχに置き換え可能です。

次に2-はψに置き換えが可能ですが、左の個数と右の個数は常に一定以上の差を保つ必要があります。例えば先程の例で、0-と3/5、2-と5/7では成り立ちません。具体的には差分が3以上になると不可能になり、差分が0だと成り立たなくなります。
不可能になる分にはルール適用がなされないだけなのでOKですが、成り立たないのは問題です。具体的には右側の個数をχ+ψ+3としていますので、両者の差は常にχ+1となり、これは0にはなりません。そのためこの状態でルールが成り立ちます。
実は文字化できるのはここまでですが実際にはもう少しだけ汎化できます。

この右下のマス数2は文字へ置き換えられはするのですが、そこに対応する置き換え箇所はχ+ψ+3/χ+ψ+5の両者の差分である2になります。つまり画像のとおりに置き換えできるはずですが、このゲームにはそんなルール設定はありませんので、できません。もしかするとしばらく進めるとできるようになるのかもしれませんが。

なので最終的にはこれくらいにしておきまして、各自の次数を下げていきます。

これで完成ではありますが、ゲームの性質上κに置き換えられなかった箇所も対応しておきます。
Bombe Rules (5):
💣⠨⢵⠯⣽⡣⡂⣯⠺⠅⡄⠂⡥⠃⠀⣲⣃⠎⠕⢠⢩⠃⣽⠐⡋⡾⢚⣶⣼⢩⡪⢳⠝⢮⠤⠿⣳⣻⣯⠰⣍⢠⡹⢬⣍⢌⠴⡈⣬⢽⣆⡅⡽⠧⡙⠏⠗⡅⣹⡒⠎⠈⡖⢤⣤⠉⣤⢗⠛⡶⡴⡹⠻⠝⣯⣆⠄⠐⠰
⢗⢈⢓⡠⢨⠻⠡⣱⠔⠵⠃⢣⠮⢆⣔⡑⢙⡀⠣⢬⠁⠉⢸⠸⣞⠳⠁⡬⠵⠞⡰⣬⣥⣠⡔⡂⠝⢰⠫⢀⡭⡍⠨⠂🛑
ではこれで六角形5-3 No.169が解けたかというと、まだ解けません。
具体的には0/2と1-の組み合わせで2-と表して良いというルールが足りません。こちらも検討します。


先程の証明の通りに上記のルールは成り立ちます。
ちなみに0/2は2-に含まれていますので、更に書き換えます。


爆弾の個数内訳は変わりません。aには一つまでしか爆弾が入らず、bにも1つまでしか爆弾が入らないからです。3-,4-にしたときも爆弾の個数内訳は変わりません。では右の1-の方はどうでしょうか?

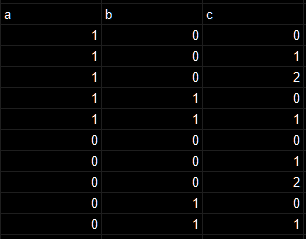
すべてのマスを通して3個以下であろうことはわかりますが、それ以上はわかりません。(2-と2-の組み合わせにおいて最大4個までありうるが、4子の場合はaに2個、cに2個のため、aが1マスしかない状態では最大3つまでになる)
なので、これはあまり先程の2-のルールを広げるような役割は持てません。あくまで右と左に差分があるときのみ、先程のようなルールが成り立つと考えるべきでしょう。

具体的にはこうなるでしょう。次数を下げます。

これで完成……と言いたいところですが実はまだ次数が下がります。

なんで!?と思うかもしれませんが事前に考えておいた2-2-の例で考えてみます。χ=0,ψ=2のとき、2-と2-の範囲について3-になる……ので事前検討の結果と一致します。では差分があるときのみ適用できるというのは何だったのでしょうか。
実は『その2つのルールは意味が違う』のです。せっかくなので画面で確認してみましょう。もし、2つのルールの意味が同じであれば、この盤面に適用してこのレベルはクリアできるはずです。


クリアできませんでした。
では一旦ルールを編集し、再度決定します。


クリアできませんでした。クリアできないのは置いておいて、盤面に追加されている情報に相違があることがわかるでしょうか。3-が2-になっているのです。つまりこの両者のルールは全く違うものなのです。今回欲しかったのは左右の爆弾の個数に差がある場合のルールなので、このまま進めます。
さて、クリアできなかったのは良いとして3/5の5が排除されていないのが気にかかります。
この記事で考察して加えたルールは以下でした。
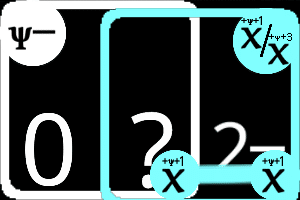
この盤面の2-と3/5の関係性は下記です。

2-だけに含まれているマスが1のため、ルール適用がされていませんでした。
そうです、最初に0/2と1-の関係性のときはあった1マスが簡略化の過程で抜けていたのですね。ではそれも踏まえて、再度ルールを見直します。



そうです、ψ-の範囲についてはすべてのマス数で成り立つのです。
実はψ-のみに含まれるマス数はこのルールの趣旨には全く関係がありません。
まず、aに含まれるマス数が0の場合について、文字だとわかりにくいが表を見てください。

この場合χは0または1しか許されません。(ψはどのような数でも許されます)
また、cは1個以上の爆弾が確定します。aが1のときも考えてみましょう。

わかりましたでしょうか。つまりaが2以上のときは常にすべて不可能なのです。ですから?にもできるのですが対して意味はなく、aに許されるマス数は1または0のみです。
上記の通りルール設定をすることで無事クリアできました。
今回作ったルールは下記です。
Bombe Rules (6):
💣⠨⢵⠯⣽⡣⡂⣯⠺⠅⣝⠂⣽⠃⠀⠲⣄⠏⠗⢀⣅⡭⠑⣕⢿⢋⠅⢭⠜⠦⢙⡸⡞⢶⡗⡺⣓⡚⡠⠓⡔⠬⢁⢁⣵⢉⢾⣉⢻⠉⣳⠠⡆⡔⢓⢺⢊⠶⢏⡟⢔⣕⡬⡵⠠⡜⢡⢒⡆⠠⢍⢵⡱⣦⣧⢉⢯⢎⣖
⠇⠈⠖⠼⡐⡆⢇⡽⡼⠒⠠⢸⠒⢐⡠⣶⢭⢝⢾⢩⡍⢰⢛⠀⣓⢊⣧⠾⠰⠂⠼⡉⠦⡨⡡⢊⣌⠁⢐⢳⠕⢃⠛⣞⡸⠀⠘⠲⠎⣣⣘⠻⠺⡹⡳⠕⡠⡓⠍⠶⢋⡎⡅🛑
一体いつクリアできるのでしょうか。先行きが不安になる歩みの遅さです。
