Bombeとかいうゲームについての手記 その21
このnoteは私が淡々と頭の中を整理するために書くnoteです。
過度な期待はしないでください。
今回検討する盤面はこちら。





前回も同じような盤面だったような……。
3ルールも結局、2ルールのときに確定しなかった事項が3つ目の要素によって確定するとかしないとかそのくらいの話なのかもしれない。
!2は0,1,3になるが、まず3はありえない。3の場合は上段1マスだけでは2/5と3/4を同時には満たせなくなる。

一応リストを示したがリストがなくても例えば下段の爆弾が3つ埋まるときは上段一つで残りの爆弾数が0/3,1/2となるので絶対に成立する組み合わせはない。
下段の爆弾が2つ埋まる場合存在せず、(!2のため)下段の爆弾が1つ埋まる場合、それぞれ残りの爆弾数が1/4,3/4の場合、1/4,2/3の場合、2/5,2/3の場合が存在する。1/4,3/4の場合は一見成立するように見えて上段のマス数が3では成立しない。1/4,2/3の場合は当然成立せず、2/5,2/3の場合のみ成立することになる。
故に下段3つのマスのうち左2つが0が確定し、右が爆弾なのである。なお3つとも爆弾でないパターンは一覧表より否定されている。
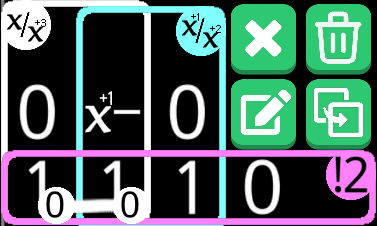
しかし全然汎用的でない。!シリーズはなんとかならんのか。
少し考察をする。!シリーズをうまく活用する方法を考えたい。!は情報量としては無いよりはマシくらいの本当に低い情報量しか持たない。例えば、
!χという情報が与えられたときに、そのマスにあり得る値は(χ-1)-,(χ+1)+である。
今回のように前提としてマス数自体が少ないということであれば、ある程度情報としての価値を持つこともある。

例えばこういうことが言える。また、!は爆弾の個数が上下に範囲が拡散していくが、例えば天井にすぐぶち当たるパターンは書き下せる。


ただしこれは大した情報ではない。具体的には3マス中に2マス以下の爆弾があるとか、本当に無いよりはマシくらいの情報も多い。
他の範囲と被ったときを考える。2ルールのときは本当になにもない。例えば1と!1を示す。

cに許容される爆弾の個数が本当に多すぎる。!を使うときはマス数でよくよく制限しなければ使えない。逆に、特定の数値を禁止すれば一気に狭まるときに使うべきである。

例えば1-,1/4を示す。ここで例えば!1とマス数制限をかける。



ここまで来ると、ようやく使えるようになる。だから!を使うときはマス数制限と!自体が3つ目のルールであることが重要である。逆に言うとそれ以外はルール化は難しいだろう。
ちなみにこの例もあまり良くない。本当は!1で2-ならば最低でも0/2であるから、そっちを使ったほうがより解けるであろう。
ちなみにこの場合と同様に大体はχ/χ+1などの表現で足りる場合もあるが、この記事で解いた問題などはその表記ができない場合のものである。具体的には0/1/3などになる場合は!2:3などと表記せざるを得ないのだ。
さてもう一問解いてみよう。


先ほど考えたことが如実に出てきていそうだ。


大前提としてaが0だとbは1/3、cが0/2である。ここで!2が示している役割は0と示せる場所の爆弾の存在否定のみである。b,cが1,2であるときに該当箇所に爆弾をいれると2になってしまう。同じくb,cが3,0であるときは該当箇所には爆弾が入らない。どちらにしても爆弾は入らない。

一般化するとこう。この場合、左の爆弾の個数はχ/χ+2であるから、下段真ん中にその数が入る。χであるとき、右側に入れなければならない爆弾は最大2個であるが、その場合は上段1個、下段1個もしくは上段2個である。そのうち下段1個は否定される。!χ+1だからである。よって常に爆弾は入らず、上段右側は0/1/2となる。




さっきの例から見ると、下段真ん中が特に確定しそう。
0の場合はあり得ない。0の場合だと!2と矛盾してしまう。なので左は実質2。

2であることが確定する場合そもそも考えなくて良い。左は2:2なので全て爆弾確定。右も1:1,2であるが!2を考えると上段にしか爆弾が入らない。

0/2:2が非常に大きな情報であるが、それ故に文字にできない。マス目もいじれない。重要なのは0/2が3に与える影響ではないのか?

これが成り立つ。他のレベルをいくつか解いてくれたが、この盤面は解いてくれなかった。



結局先程と同じだ。まあさっきの0/2と3の関係性はあくまで読み返しているだけであってなにか情報が増えているわけではないので当たり前か……。

これはχ=1のときあり得るのだろうか?
その場合はそもそも!3になるし下段が2-確定で、χ+3が4、χ+1/χ+3は2/4で4は不可能になってしまう。成り立つかもしれないが情報の質が全部高まるのでこのルールでなくても解けてしまいそうだが……。
CPUにやさしくχは使わないでおく。
もう1盤面。



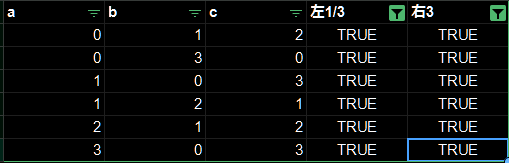
なおこれはツールの話になるが、偶数からb+cの一部をフィルタすれば0/2/4なども表現できる。

なおa+b+cが3でないものはこちら。3であるもののほうが少ない。

具体的にはこのパターンのみ。

マス数の都合を入れるとたまたまaが1のときが3みたいです。たまたまにしか思えないんだがこれはどう汎化すれば……。

とりあえず偶数までは拡張できるのでこれで……。
