Bombeとかいうゲームについての手記 その7
このnoteは私が淡々と頭の中を整理するために書くnoteです。
過度な期待はしないでください。




ということは、この2の範囲にかかる1/4と1/3についてはそれぞれ4,3の可能性は無い。何故ならば、

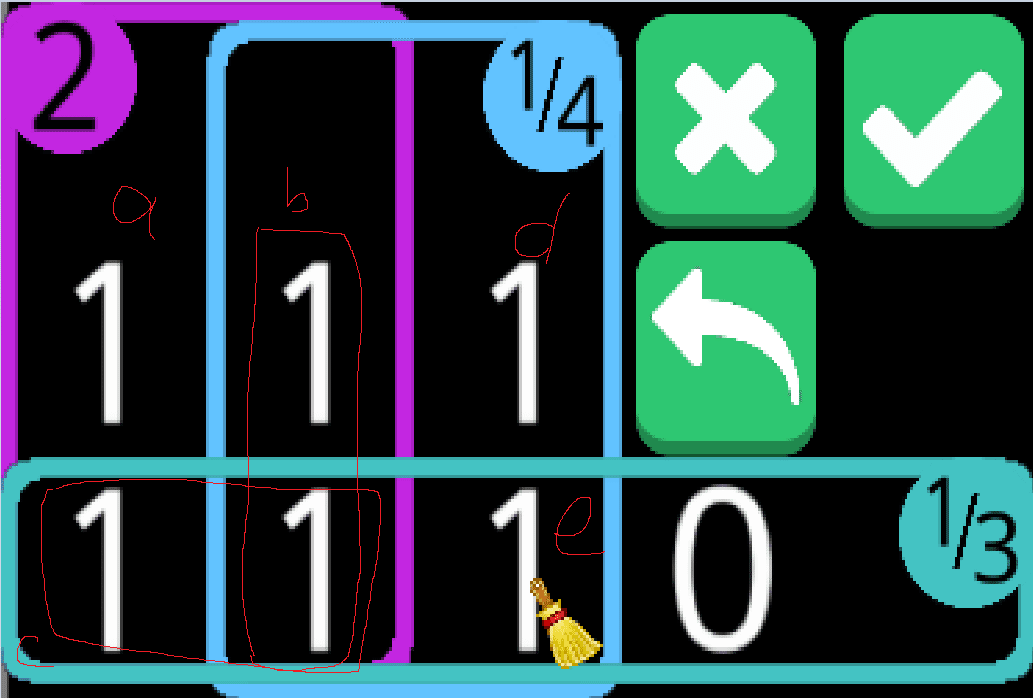
このような盤面においてbとcはそれぞれ4,3であるとき常に2である。なのでまずそれぞれの範囲が4,3というパターンは存在しない。次に1,3または4,1のパターンだが、それも存在しない。例えば4であるとき、すでに1/3の範囲には2個以上爆弾が入ってしまう。そのため、それも不可能である。3である場合も同様。


このχの次数は下げられない。これはχ=0すなわち0/3,0/2の場合は先程の推論は成り立たないからである。

χ=1の場合を検討する。

2/5では5自体がありえないので、2に確定する。

一方で2/4としたときに、d,e,fの内訳を考えると、表のとおりになるが、dに3以上の爆弾が確定した場合不可能である。(情報指定:2に反する)
dが2である場合もeに爆弾が入るため、やはり不可能である。つまり2の爆弾の個数については2以下という指定さえあれば良い。


次にχ=2の時を考える。

こちらも3/6の6はありえない。

先程と同様にdのいちに2以上入る場合は不可能であるので、こちらもやはり成り立つ。
ということは、3/6から6を除き、かつ3/5から5を除くことができるのはdのいちの爆弾の個数が2-に合致しない場合である。その場合とは、具体的には3/5が3+であるとき、3であることが成り立つ。つまり

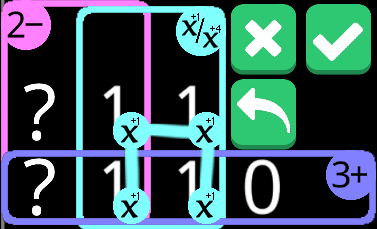
このようになる。逆に3/5の方から見て5でないことも明らかなので、

これも成り立ち、かつ

この条件でも成り立つ。

また、上記の3+に置き換えたルールとχ+1/χ+3としたルールでは3+のほうが適用範囲が広い。χ=0のとき1/3であるが、χ+1/χ+3とχ+1/χ+4のお互いにその関係が適用されるため、どちらもχ+3とχ+4が否定されるというだけに過ぎない。この状態の盤面について再度個数を検討する。


この一覧表の結果からしてa-bは常に0である。これは成り立つ。bは常に爆弾の個数が0以外では成り立たないので、bのマス数は?でよい。
また、c,eもマス数は?でよい。これはcを1以外のマス数にしたところで内訳表が変わらないためである。(cの爆弾の個数は他のマスの個数で決まる)
eについては一見爆弾の個数が変わりそうだが、実は変わらない。これは2-の範囲内にあることにより、d+eの爆弾の個数に制限があるため。具体的にはeに3個以上入れられない。唯一増えるパターンであるd=0,e=2,f=1の場合はd=1,e=1,f=1の場合と同じ内訳になる。

Bombe Rules (6):
💣⠨⢵⠯⣽⡣⡂⣯⠺⠅⠨⠃⣽⠃⠀⣂⡃⠎⠖⢠⢩⠍⣽⠠⢶⢙⡇⡚⣶⢣⣪⣲⢄⡐⡤⠟⢴⣦⣿⢉⠂⢍⣠⣧⢓⢑⡽⠣⠾⣽⢃⣨⢿⡠⡑⢖⠞⡋⠉⢕⣬⢀⣘⡹⠏⠭⣬⢀⡴⣲⡖⣆⢪⠱⠁⠗⠰⢁⡁
⣖⢬⢐⡛⢐⢂⠏⠍⠓⡐⠤⠐⠛⡺⠯⠰⢘⠜⡹⠋⣖⠶⠊⡦⠇⣢⢙⣨⠀⡰⡊⢁⢏⣐⠜⡊⡘⠑⢪⡒⡻⡣⠅⢃⠌⡰⠀⠕⢌⡥⠸⡩⠀⣯⣭⠫⣼⡨⠀⡶⡛⡯⢊🛑
一応元の問題は解けたがこれでよいのだろうか……。
