Bombeとかいうゲームについての手記 その10

このnoteは私が淡々と頭の中を整理するために書くnoteです。
過度な期待はしないでください。

いつになったらクリアできるんだこのゲームは。
今回の考察対象はこれ。

この盤面では1の範囲の内訳が確定しているらしいです。

b,cについて爆弾が入っていると仮定すると、bに爆弾が入っている場合はcに爆弾が入らず、cに爆弾が入っている場合はbに爆弾が入らない。その場合、aに爆弾を1つ入れなければならないが、そうするともう一つの1/3に反する。(2個になってしまう)

また、a,b,c,dのマス数は関係ない。そしてbとcの間のマスは0でなくてもよく、何マスでも良い。仮にここに爆弾が入る場合であってもbとcが0なのは揺るぎない。(ただしdの爆弾は確定しなくなる)

1/3を2/4へ変更して検討する。
マス目の都合上実質2/4は2。

この場合は逆にdは常に0。(ちなみにb-cの間のマスも0。)

先程と同様にマス目の数によらず、爆弾の位置が定まるため、他のマス目は?にできる。

今回のルールに限らず、マス目によらない場合(?にできる場合)とは、爆弾の個数・位置だけ定めれば自動的に他の爆弾の個数・位置が確定する盤面だということかもしれない。内訳表はどちらかというとそういった考え方に適するようだ。
また、前回取り扱ったようなχ-のマス目が指定されている場合がある。

前回の盤面とルール

このような場合のχ-の意味合いとしては『そのマス以外のマスに爆弾の個数からχ個引いた個数の爆弾が最低でも入る』という意味でこのような表現になるのだろう。

話が横道にそれたが、検討対象の盤面に話を戻そう。
今回のここまでの検討での感想は一つ。
『もしかして、偶数か奇数かで判定してない？』

おそらくしているだろう。少なくとも最初のルールについては奇数の範囲2つと1に拡張できた。この盤面で考えてみる。

以上より、b-dには爆弾が入らず常に0個である。またc-eについては常に爆弾が一つ入る。

さて、1を2とした場合はどうだろうか。

ここで改めて偶奇の関係性を示すと、
偶数:奇数+奇数もしくは偶数+偶数で成り立つ
奇数:偶数+奇数のみで成り立つ
という関係性になっている。

さて、爆弾の内訳を考えると、
どれかのマスに2つ入るパターンが4通り
別のマスに一つずつ入るパターンが4C2=6通り
合計10通り
書き出すとこのようなパターン。

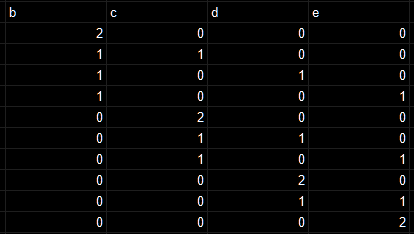
それぞれのパターンに応じたaの数を考えていくと、

不可能になるのはb-eまで埋めた時点で左右の偶数奇数が相違している場合である。具体的には同じマスに2個爆弾が入っている場合は0/2でどちらにしても偶数になるので成り立つ個数が存在するが、違うマスに1つずつ入っている場合で、b,dに入っているなどの左右対称盤面以外では成り立たない。
ここで、すべての数を偶数もしくは奇数で表すことにしてみる。

重複があることに注意。

上記は重複削除したもの。具体的には同じマスに2つ爆弾が入っている場合はすべて爆弾の個数が偶数であるので重複。
さて、このときにどんなことが言えるだろうか。

このようになる。
さて問題はこの結論から1のときの結論と合わせてどのような事実が導かれるかであるが……。

結果を並べただけ

『bとdの偶奇は必ず一致する』というところだろうか。
その場合、bとdの偶奇は何により定まるかを指定できなければルールにならない。
『bとdの偶奇は、a+cの偶奇を反転させたものと必ず一致する』というところだろうか。ではa+cは何により定まるのであろうか。
やはり具体的な数に確定させるのは一般化では難しいだろうか。少なくとも1と2の範囲内ではなにか具体的な数を指定できそうになかった。(もともと今回の検討が偶奇関係に偏っているせいもある)

上記ルールが成り立った。そしてよく考えてみれば、右下の爆弾の個数は全く意味がない。偶数であろうと奇数であろうとb,c,d,eへの爆弾の入れ方が偶数か奇数かでしか推論していないのだから、そもそも爆弾の個数は何でもいいはずである。

このルールではψで上部の範囲の爆弾の個数が統一されているが、コレが異なる場合はどうだろうか。例えば、

こういう場合である。このまま続けて検討していく。ただ文字がたくさん入っていると考えるのが面倒なので適当に代入してみる。
χ+2*=1, ψ=1, κ=2とする。

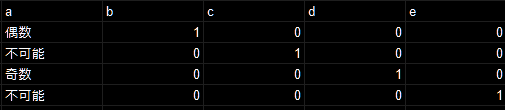
この通りになる。
この場合は常にaとdの偶奇が一致して、aとbの偶奇が一致しない。
また、c,eは常に0である。

いじくり回していたら見つけてしまったものを先に示す。

なお、左上と右上に1しか差がない偶奇関係のときのみに成立するルールであるように見えるが、実際には偶数か奇数かだけで成立する。
(χ+2*∈(χ+2)+2*が成り立つため)

また左右の対称性を鑑みるにコレも成り立つ。
右下の爆弾の個数が1であることはなんとかできないであろうか？
先程の実際の例に戻って、右下の爆弾の個数が2であるときを考える。

b,c,d,eについて爆弾が2個である場合のパターンはすでに検討済み。

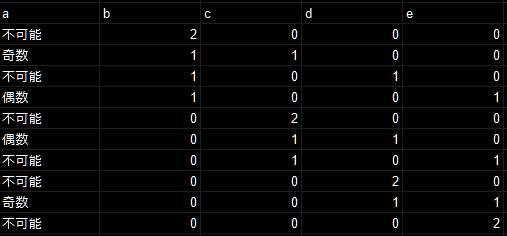
上記のような内訳になる。

実は1のときとは不可能になるパターンが反転している。

先程と同様に偶数奇数に変更した後に重複を削除したもの。
重複3つ、1のときに成立したものが3つ、2のときに成立したものが4つで合計10個。これは2この爆弾をb,c,d,eに配置したときのすべてのパターン数と一致する。(ので正しそう)
この結果から何か読み取れるだろうか。b,c,d,eについて常に奇数が2つ以上ある。これはつまり一つの箇所に2個入るパターンは存在しないということである。しかしこれも2だからそうなのであって一般的に成り立つわけではない。

b,c,d,eはそれぞれ1-

2以上の偶数で成り立つわけではない

もちろんそれぞれのマスが奇数個であるわけでもない

偶数のときはなにか意味のあるルールは成り立たない、ということだろうか。偶奇が一致している範囲が2つ被った状態が特別に意味を持てるということだろうか。とにかく得られたルールは先程の偶奇が一致している範囲が2つ被った状態で他の範囲が被っているときのみであった。